2. 上海蓝诺新能源技术有限公司
2. Shanghai Azureve Technology Co., Ltd.
0 引言
往复压缩机是石油化工领域的关键设备[1],其结构复杂,作业环境恶劣,容易发生故障而导致严重后果[2]。根据振动信号特征指标变化来判断往复压缩机运行状态是否异常,通常要求其运行转速稳定。这是因为转速变化时,振动信号的特征指标将呈现多变性和不稳定性,从而严重影响诊断的正确率。
实际上,往复压缩机的转速会根据工作要求而发生改变,因此对变转速往复压缩机的特征分析显得尤为重要。此外,为了充分挖掘振动信息,通常需要提取大量特征,组成高维特征向量,从而导致信息冗余,影响分析的正确率和效率。因此,在变转速的振动信号中挖掘出能表征设备健康状态的相关特征,对于故障诊断具有重要意义[3]。本文引入关联规则方法来挖掘变转速往复压缩机的振动信号特征。
关联规则是数据挖掘的重要方法[4],可以很好地挖掘数据之间的关系,并且能够发现潜在的有意义的信息[5]。传统的关联规则挖掘方法针对基于Apriori算法的布尔型数据,而振动信号大多是量化属性值[6],需要通过离散化方法将数据映射到区间,将量化值转变为布尔型数据[7]。常见的均匀划分区间会出现边界过硬的问题[8]。将模糊数学用于划分区间可以解决边界过硬的问题,但同时也会产生隶属度和隶属函数难确定的问题[9]。使用聚类方法进行数据挖掘,忽略了数据之间的关系[10]。为此,本文提出一种等概率关联规则的划分方法,用于挖掘往复压缩机状态的相关特征,分析不同转速特征及其变化关系,并通过试验,分析不同转速下曲轴间隙故障的相关特征,以期为压缩机状态诊断提供依据。
1 研究方法 1.1 关联规则关联规则挖掘在1993年由R.AGRAWAL等[11]首先提出,是知识发现(Knowledge Discovery in Database, KDD)研究的重要内容。用关联规则进行优劣评价的标准主要是支持度和置信度[12]。
1.2 等概率关联规则借鉴符号近似聚合(Symbolic Aggregate Approximation,SAX)中的区间划分和符号化思想,根据数据分布特点,将振动信号的特征值等概率划分成若干区间,将不同的区间用不同的符号表示,实现连续量化属性值向离散布尔值的转变。
将数据按式(1)进行标准化处理,标准化后的数据服从高斯分布X~N(0,1)。
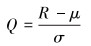
|
(1) |
式中:Q 是序列R 标准化后的数据,μ和σ分别是序列R的均值和标准差。
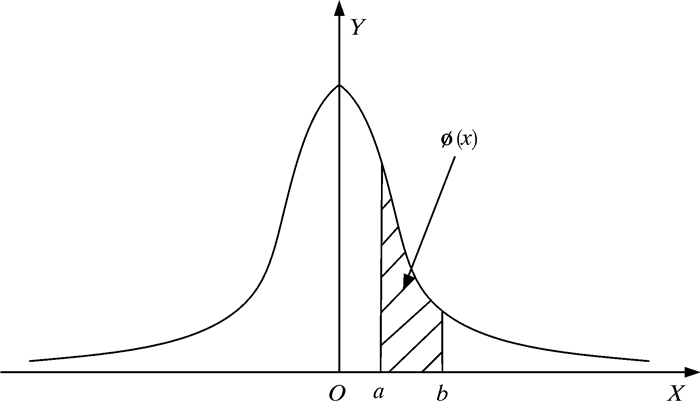
当数据服从高斯分布时,数据点落在[a, b]范围内的概率为标准高斯分布曲线所包围的区域,如图 1所示。
|
| 图 1 高斯分布概率 Fig.1 Gaussian distribution probability |
概率公式为:
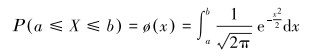
|
(2) |
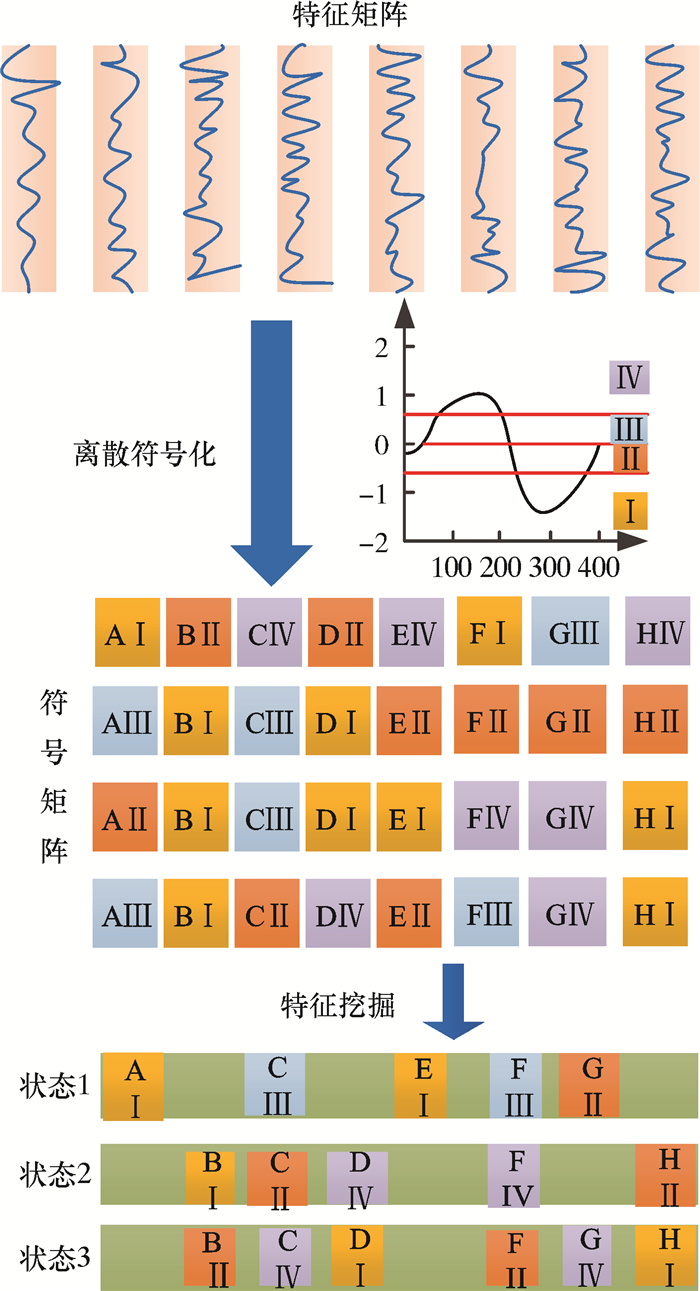
根据高斯分布的特点,可以采用等概率分布的形式对数据进行区间划分,将每个区间用一个符号表示,这样原始的特征矩阵就转变为由一系列代表不同特征和不同级别的符号组成。通过Apriori算法对符号化后的特征区间和状态标签组成的符号矩阵进行规则挖掘,找出转速与特征之间的关系。等概率关联规则方法如图 2所示。
|
| 图 2 等概率关联规则方法示意图 Fig.2 Schematic diagram of the method of equal probability association rules |
图 2中每个方格代表一个特征区间,字母“A、B、C、……”代表特征值的类型,“Ⅰ、Ⅱ、Ⅲ、……”代表区间值的级别高低,级别越高,表示区间值越大。最终可以挖掘出每一种转速相对应的特征及特征值范围,据此可以分析不同转速的敏感特征以及特征值随转速的变化情况。
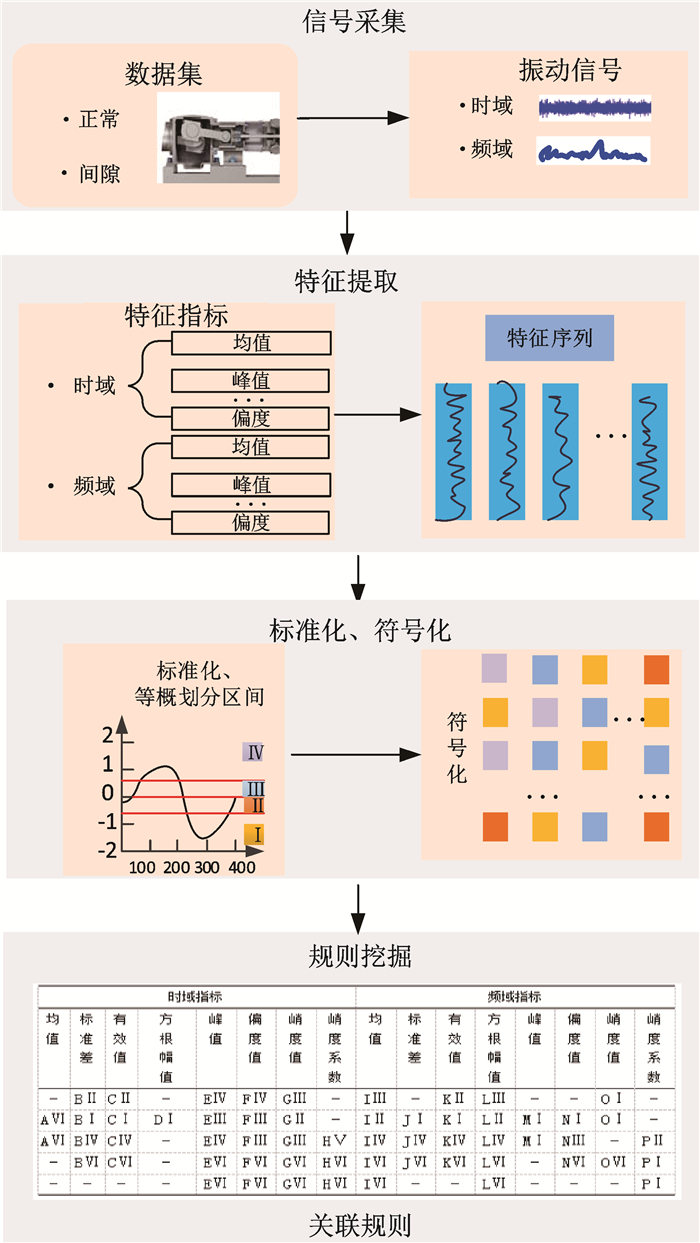
2 基于等概率关联规则的特征挖掘 2.1 挖掘流程整个挖掘过程可分为信号采集、特征提取、特征向量标准化、符号化处理及规则挖掘等4个步骤,具体方法流程如图 3所示。
|
| 图 3 基于等概率关联规则的挖掘流程图 Fig.3 The mining flow chart based on equal probability association rules |
图 3中“A、B、C、……”,“Ⅰ、Ⅱ、Ⅲ、……”与图 2中符号含义相同,“-”表示无。首先采集往复压缩机正常和间隙故障不同转速的振动信号,然后对振动信号提取时域和频域特征,组成特征序列,将特征向量进行标准化处理,按照等概率将特征向量进行离散化,转化为符号序列,最后运用Apriori算法对符号化的特征区间和状态标签进行规则挖掘,确定往复压缩机不同转速与特征值之间的关联关系。
2.2 振动信号特征指标提取往复压缩机振动信号为非平稳信号,使用时域和频域分析获取振动信号特征指标[13]。本文提取8个时域特征和8个频域特征,如表 1所示。表 1中所示特征指标为时域和频域所共有,i∈[1, n]
| 特征指标 | 描述 |
| 均值 | 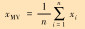 |
| 标准差 | 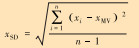 |
| 有效值 | 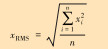 |
| 方根幅值 | 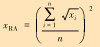 |
| 峰值 | xCF=maxxi |
| 偏度值 | 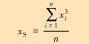 |
| 峭度值 | 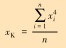 |
| 峭度系数 | 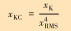 |
3 实例分析 3.1 试验装置及数据采集
采用中国石油大学(北京)故障诊断实验室的RCK-1往复式压缩机试验台采集试验数据,对所提出的方法进行分析和验证。模拟试验台如图 4所示。

|
| 图 4 往复压缩机故障模拟试验台 Fig.4 Reciprocating compressor fault simulation test bench |
压缩机试验台是小型单缸双冲程工业往复式压缩机。它模拟的机械故障是在曲轴与连杆连接处存在故障间隙(即间隙过大或过小),从而引发传动系统故障。试验中,振动加速度传感器安装在曲轴箱上方的轴承座上,采样频率为20 kHz。在不同转速(80、100和120 r/min)下,采集间隙正常(即曲轴销直径15.88 mm)和间隙故障共15种状态下的样本900组,每组样本长度为20 000。其中450组样本用来进行数据挖掘,另外450组样本用来进行测试。
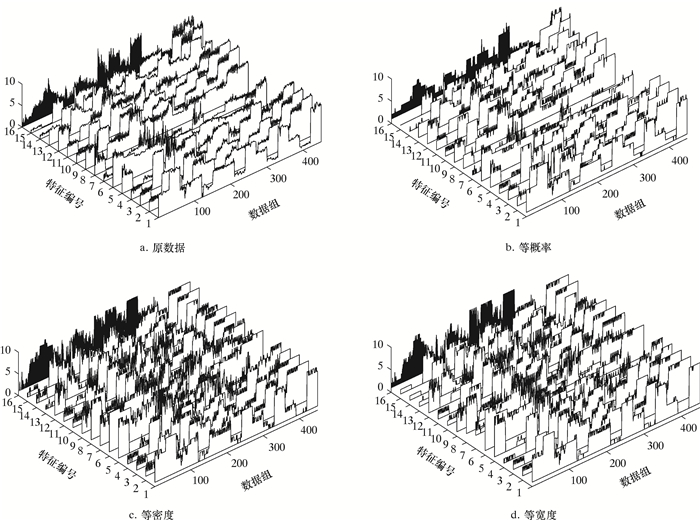
3.2 基于等概率的数据离散化处理对采集的每个样本提取2.2节中提到的8个时域特征和8个频域特征,组成450×16的特征值矩阵。将每一列特征值看作一个长度为450的特征序列,按照等概率方法,设置符号集为10进行离散化。同样用等密度和等宽度方法进行离散化,然后将数据进行归一化,画出分布图,如图 5所示。
|
| 图 5 离散化数据对比 Fig.5 Discretization data comparison |
对数据进行等概率离散化处理是为了既可以保留数据原有的特征分布,又可以将数据进行规则化处理,便于使用关联规则进行特征挖掘。从图 5可以看出, 等概率离散化效果最好,既保留了原始数据的数据分布特点,又使数据变得平滑,利于关联规则挖掘。
信息熵可以评价信号所含信息量的大小[14]。本文采用区间类信息熵方法对离散化效果进行量化对比。
第i个区间类信息熵Ii的定义如下[15]:
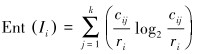
|
(3) |
式中:k为类别个数,cij为第i个区间中类别为j的事例个数,ri为第i个区间中总的事例个数。
信息熵的大小与区间类别的混杂程度成正比,信息熵越小,区间中类别混杂程度越低,离散化效果越好。信息熵为0时,表明区间中只有一个类别,离散化效果最好。
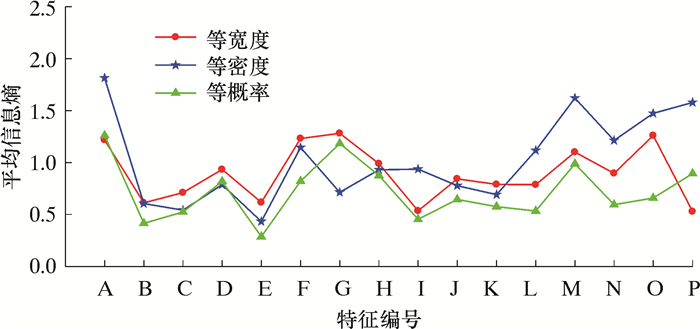
下面用等密度、等宽度以及等概率离散化方法对数据进行离散化。对每列特征数据划分10个区间,共16个特征,得到16×10的数据方阵,共160个符号,然后对区间进行类信息熵计算,得到16×10的信息熵矩阵,将计算结果按特征计算平均信息熵,如图 6所示。从图 6可以看出,采用等概率方法进行离散化处理得到的平均信息熵最小,效果最好。因此,本文选用等概率方法对数据进行离散化处理。
|
| 图 6 不同离散化方法的信息熵对比 Fig.6 Comparison of information entropy of different discretization methods |
3.3 关联规则挖掘结果分析
将3.2节特征矩阵中的160个符号和15种往复压缩机状态作为包含175个项的项集,每一条数据的符号向量和状态类型作为一个事物,构建成包含450组事物的事物集。利用基于Aprior的关联规则挖掘方法进行挖掘,设置支持度为0.7,置信度为0.7。由于对数据进行挖掘主要是为了得到状态与特征之间的关系,所以设置规则的后项为15种往复压缩机状态。经挖掘得到状态与特征之间的诊断关系规则,如表 2所示。
| 时域指标 | 频域指标 | 状态 | |||||||||||||||
| 均值 | 标准差 | 有效值 | 方根幅值 | 峰值 | 偏度值 | 峭度值 | 峭度系数 | 均值 | 标准差 | 有效值 | 方根幅值 | 峰值 | 偏度值 | 峭度值 | 峭度系数 | ||
| AⅥ | BⅡ | CⅡ | DⅡ | - | FⅩ | GⅡ | - | - | - | - | - | MⅡ | NⅡ | OⅡ | - | 1 | |
| AⅩ | BⅠ | CⅠ | DⅠ | EⅠ | FⅨ | GⅡ | HⅢ | IⅠ | JⅠ | KⅠ | LⅠ | MⅠ | NⅠ | OⅠ | PⅠ | 2 | |
| - | BⅥ | CⅥ | - | EⅡ | - | GⅢ | HⅡ | - | - | KⅥ | LⅥ | - | NⅥ | - | - | 3 | |
| - | BⅡ | CⅡ | - | EⅡ | FⅦ | GⅢ | - | - | - | KⅡ | - | - | NⅡ | OⅡ | - | 4 | |
| - | BⅢ | CⅢ | DⅢ | EⅢ | - | GⅢ | - | IⅢ | JⅢ | - | LⅠ | MⅢ | NⅢ | - | - | 5 | |
| - | BⅤ | CⅤ | DⅧ | EⅤ | - | - | HⅡ | - | JⅤ | KⅤ | - | - | - | - | - | 6 | |
| - | BⅢ | CⅢ | - | - | - | GⅢ | - | - | - | KⅢ | - | - | NⅡ | OⅢ | - | 7 | |
| - | BⅣ | CⅣ | DⅥ | EⅥ | - | GⅥ | HⅥ | - | JⅥ | KⅣ | - | - | NⅢ | - | - | 8 | |
| - | - | CⅦ | DⅧ | EⅦ | FⅦ | GⅢ | HⅦ | - | - | KⅦ | - | - | - | - | - | 9 | |
| - | BⅡ | CⅡ | DⅡ | - | - | - | - | - | JⅡ | KⅡ | - | MⅣ | NⅡ | OⅡ | PⅡ | 10 | |
| - | BⅤ | CⅤ | DⅤ | EⅤ | FⅤ | GⅤ | - | - | JⅤ | KⅤ | - | - | - | OⅤ | PⅩ | 11 | |
| AⅨ | BⅧ | CⅧ | DⅨ | - | - | GⅤ | - | IⅥ | JⅧ | KⅧ | LⅧ | - | NⅧ | - | - | 12 | |
| - | BⅤ | - | DⅤ | EⅤ | - | GⅤ | HⅤ | IⅨ | JⅤ | - | LⅤ | - | NⅤ | OⅤ | - | 13 | |
| AⅡ | - | CⅨ | DⅨ | - | - | GⅨ | IⅨ | - | JⅨ | KⅨ | LⅨ | - | NⅨ | - | - | 14 | |
| AⅩ | BⅩ | CⅩ | - | EⅩ | - | GⅩ | - | - | JⅩ | KⅩ | - | - | NⅩ | OⅩ | - | 15 | |
以表 2为例,前项中,“A,B,C,……, P”分别代表 2.2节提到的8个时域特征和8个频域特征,“Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ、Ⅸ、Ⅹ”分别代表特征值区间级别大小,依次增大,“-”表示无。后项中,数字1~15分别代表往复压缩机曲轴销直径为15.88、15.83、15.81、15.78和15.63 mm时,转速80、100及120 r/min的15种状态。表 3为转速相同时,不同状态与特征之间的关系规则。表 3中各符号含义与表 2中各符号含义相同。通过对表 2和表 3进行分析,挖掘出转速敏感特征、故障敏感特征以及转速和故障共同敏感特征。
| 时域指标 | 频域指标 | 状态 | |||||||||||||||
| 均值 | 标准差 | 有效值 | 方根幅值 | 峰值 | 偏度值 | 峭度值 | 峭度系数 | 均值 | 标准差 | 有效值 | 方根幅值 | 峰值 | 偏度值 | 峭度值 | 峭度系数 | ||
| AⅥ | BⅡ | CⅡ | DⅡ | - | FⅩ | GⅡ | - | - | - | - | - | MⅡ | NⅡ | OⅡ | - | 1 | |
| - | BⅡ | CⅡ | - | EⅡ | FⅦ | GⅢ | - | - | - | KⅡ | - | - | NⅡ | OⅡ | - | 4 | |
| - | BⅢ | CⅢ | - | - | - | GⅢ | - | - | - | KⅢ | - | - | NⅡ | OⅢ | - | 7 | |
| - | BⅡ | CⅡ | DⅡ | - | - | - | - | - | JⅡ | KⅡ | - | MⅣ | NⅡ | OⅡ | PⅡ | 10 | |
| - | BⅤ | - | DⅤ | EⅤ | - | GⅤ | HⅤ | IⅨ | JⅤ | - | LⅤ | - | NⅤ | OⅤ | - | 13 | |
| AⅩ | BⅠ | CⅠ | DⅠ | EⅠ | FⅨ | GⅡ | HⅢ | IⅠ | JⅠ | KⅠ | LⅠ | MⅠ | NⅠ | OⅠ | PⅠ | 2 | |
| - | BⅢ | CⅢ | DⅢ | EⅢ | - | GⅢ | - | IⅢ | JⅢ | - | LⅠ | MⅢ | NⅢ | - | - | 5 | |
| - | BⅣ | CⅣ | DⅥ | EⅥ | - | GⅥ | HⅥ | - | JⅥ | KⅣ | - | - | NⅢ | - | - | 8 | |
| - | BⅤ | CⅤ | DⅤ | EⅤ | FⅤ | GⅤ | - | - | JⅤ | KⅤ | - | - | - | OⅤ | PⅩ | 11 | |
| AⅡ | - | CⅨ | DⅨ | - | - | GⅨ | IⅨ | - | JⅨ | KⅨ | LⅨ | - | NⅨ | - | - | 14 | |
| - | BⅥ | CⅥ | - | EⅡ | - | GⅢ | HⅡ | - | - | KⅥ | LⅥ | - | NⅥ | - | - | 3 | |
| - | BⅤ | CⅤ | DⅧ | EⅤ | - | - | HⅡ | - | JⅤ | KⅤ | - | - | - | - | - | 6 | |
| - | - | CⅦ | DⅧ | EⅦ | FⅦ | GⅢ | HⅦ | - | - | KⅦ | - | - | - | - | - | 9 | |
| AⅨ | BⅧ | CⅧ | DⅨ | - | - | GⅤ | - | IⅥ | JⅧ | KⅧ | LⅧ | - | NⅧ | - | - | 12 | |
| AⅩ | BⅩ | CⅩ | - | EⅩ | - | GⅩ | - | - | JⅩ | KⅩ | - | - | NⅩ | OⅩ | - | 15 | |
从表 2可以看出,时域均值、偏度值、峭度系数,频域均值、方根幅值、峰值和峭度系数这7个指标不稳定,难以表征设备运行状态,故不能作为特征指标。
曲轴销直径为15.88 mm时,随着转速的增加,特征值级别先减小后增加,曲轴销直径为15.83、15.81、15.78和15.63 mm时所产生的间隙大小和特征值级别均随着转速的增大而增大。由表 2挖掘出转速敏感特征为B、C、D、J、K、N,分别是时域标准差、有效值、方根幅值,频域标准差、有效值、偏度值。
从表 3可以看出,转速相同时,随着间隙的增大,特征值的级别呈现增大趋势,不同转速的特征值级别增大程度不同。转速为80 r/min时,随着间隙的增大特征值级别并未有明显增大,基本在Ⅱ、Ⅲ级,曲轴销直径为15.63 mm时级别有较明显增大,为Ⅴ;转速为100和120 r/min时,随着故障间隙的增大,特征值级别呈现较明显的增大趋势;转速为80 r/min时,表征曲轴销直径大小产生间隙故障的特征指标有B、C、D、G、N、O,分别是时域标准差、有效值、方根幅值、峭度值,频域偏度值、峭度值;转速为100 r/min时,表征曲轴销直径大小产生间隙故障的特征指标有B、C、D、E、G、J、K、N,分别是时域标准差、有效值、方根幅值、峰值、峭度值,频域标准差、有效值、偏度值;转速为120 r/min时,表征曲轴销直径大小产生间隙故障的特征指标有B、C、E、G、J、K、N,分别是时域标准差、有效值、峰值、峭度值,频域标准差、有效值、偏度值。故挖掘出间隙故障敏感特征为B、C、G、N,分别是时域标准差、有效值、峭度值和频域偏度值。
综合转速和间隙故障对特征值变化的影响,可以挖掘出转速和间隙故障共同敏感特征为B、C、N,分别是时域标准差、有效值和频域偏度值。采用等概率关联规则方法对数据进行规则挖掘,实现了16维特征矩阵到3维特征矩阵的降维。为了验证挖掘得到的3维指标的有效性,将每类样本30组用来训练,30组用来测试,采用SVM进行分类,分别选用16维特征和3维特征进行多组测试,求分类准确率的平均值。测试结果如表 4所示。从表 4可以看出,在利用3维特征矩阵进行不同测试变量诊断时,由于避免了信息冗余,三组测试均提高了识别率,取得了较好的分类效果。
| 测试变量 | 平均准确率/% | |
| 原始特征 | 等概率方法 | |
| 转速不同 | 98.2 | 99.5 |
| 间隙不同 | 87.3 | 90.2 |
| 转速和间隙均不同 | 95.7 | 99.5 |
工业应用中的往复压缩机不同转速、不同间隙故障数据较少,某些转速或者间隙故障的数据缺失。若不能通过实际应用的往复压缩机获取转速和间隙故障特征数据库时,则可通过仿真建模或通过同种类型试验设备进行试验,对试验数据进行挖掘得到规则库。本文采用依据数据分布概率进行离散化的等概率方法获得符号集,不同组数据在数据差值和数据范围上对获得符号集没有影响,且采用关联规则进行数据挖掘时是建立在符号集基础上,所以本文提出的等概率关联规则挖掘方法对试验数据和工业设备之间的数据通用具有良好的鲁棒性,可进行实际应用。
4 结论(1) 提出了基于等概率关联规则的变转速往复压缩机特征挖掘方法。该方法将连续的振动信号有效地离散化、符号化,然后利用关联规则挖掘转速与相关特征之间的变化关系,进行特征选择。
(2) 提出的等概率方法对往复压缩机振动信号进行离散化处理,相比于等宽度和等密度对数据进行离散化处理的方法,离散化效果更好、区间保留的信息更有效。
(3) 应用本文方法挖掘出往复压缩机的转速敏感特征、故障敏感特征以及转速和故障共同敏感特征,并将挖掘结果用于往复压缩机状态诊断,通过诊断效果对比可以看出,基于等概率关联规则挖掘得到的特征向量可以有效提高往复压缩机状态诊断的准确率。
| [1] |
段礼祥, 张来斌, 王朝晖. 往复压缩机剩余寿命预测方法及展望[J]. 石油机械, 2008, 36(10): 80-83. DUAN L X, ZHANG L B, WANG Z H. Prediction method and prospect of residual life of reciprocating compressor[J]. China Petroleum Machinery, 2008, 36(10): 80-83. |
| [2] |
黄君玲, 张来斌, 段礼祥. 基于状态监测和故障诊断的RCM技术[J]. 石油机械, 2011, 39(4): 60-63. HUANG J L, ZHANG L B, DUAN L X. RCM technology based on condition monitoring and fault diagnosis[J]. China Petroleum Machinery, 2011, 39(4): 60-63. |
| [3] |
王雪松, 潘杰, 程玉虎. 知识迁移学习方法及应用[M]. 北京: 科学出版社, 2016: 2-3. WANG X S, PAN J, CHENG Y H. Knowledge transfer learning method and application[M]. Beijing: Science Press, 2016: 2-3. |
| [4] |
谭锋奇, 李洪奇, 孟照旭, 等. 数据挖掘方法在石油勘探开发中的应用研究[J]. 石油地球物理勘探, 2010, 45(1): 85-91. TAN F Q, LI H Q, MENG Z X, et al. Application of data mining method in petroleum exploration and development[J]. Oil Geophysical Prospecting, 2010, 45(1): 85-91. |
| [5] |
白堂博, 张来斌, 王旭铎, 等. 基于SAX的关联规则挖掘方法在故障诊断中的应用[J]. 石油机械, 2017, 45(1): 70-74. BAI T B, ZHANG L B, WANG X D, et al. Application of SAX-based association rule mining on fault diagnosis[J]. China Petroleum Machinery, 2017, 45(1): 70-74. |
| [6] |
DUAN L X, ZHANG Y L, WANG X D, et al. A hybrid approach of symbolic aggregate approximation and bitmap:application to fault diagnosis of reciprocating compressor valve[J]. Journal of Vibroengineering, 2016, 18(7): 4354-4368. DOI:10.21595/jve.2016.16903 |
| [7] |
SRIKANT R, AGRAWAL R. Mining quantitative association rules in large relational tables[C]//Proceedings of the ACMSIGMOD Conference on Management of Data. New York: ACM Press, 1996: 1-12.
|
| [8] |
李乃乾, 沈钧毅. 量化关联规则挖掘及算法[J]. 小型微型计算机系统, 2003, 24(12): 2275-2277. LI N Q, SHEN J Y. Algorithms for mining quantitative association rules[J]. Mini-Micro Systems, 2003, 24(12): 2275-2277. DOI:10.3969/j.issn.1000-1220.2003.12.055 |
| [9] |
王素格, 郭晓敏, 张少霞. 基于模糊关联规则的汽车评价知识构建及应用[J]. 山西大学学报(自然科学版), 2016, 39(3): 423-428. WANG S G, GUO X M, ZHANG S X. Knowledge construction and application for car evaluation based on fuzzy association rules[J]. Journal of Shanxi University(Nature Science Edition), 2016, 39(3): 423-428. |
| [10] |
闫明月, 侯忠生, 高颖. 一种面向布尔时间序列的关联规则挖掘算法[J]. 控制与决策, 2012, 27(10): 1447-1451. YAN M Y, HOU Z S, GAO Y. Algorithm of mining association rules for binary time series[J]. Control and Decision, 2012, 27(10): 1447-1451. |
| [11] |
AGRAWAL R, IMIELINSKI T, SWANMI A N. Mining association rules between sets of items in large databases[C]//Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data. Washington: [s.n.], 1993: 207-216.
|
| [12] |
张玺.数据挖掘中关联规则算法的研究与改进[D].北京: 北京邮电大学, 2015. ZHANG X. Research and improvement of association rules algorithm in data mining[D]. Beijing: Beijing University of Posts and Telecommunications, 2015. |
| [13] |
胡瑾秋, 张来斌, 梁伟, 等. 基于谐波小波分析的管道小泄漏诊断方法[J]. 中国石油大学学报(自然科学版), 2009, 33(4): 118-124. HU J Q, ZHANG L B, LIANG W, et al. Small leakage detection of long distance pipeline based on harmonic wavelet analysis[J]. Journal of China University of Petroleum (Edition of Natural Science), 2009, 33(4): 118-124. DOI:10.3321/j.issn:1673-5005.2009.04.023 |
| [14] |
潘和平, 樊政军, 马勇. 基于信息熵识别油气层和水层的聚类方法[J]. 石油大学学报(自然科学版), 2004, 28(6): 31-34. PAN H P, FAN Z J, MA Y. Clustering method for oil(gas)-bearing formation and water bearing formation based on information entropy[J]. Journal of the University of Petroleum, China(Edition of Natural Science), 2004, 28(6): 31-34. |
| [15] |
梁红旗. 数值属性离散化方法研究[J]. 信息技术, 2008(5): 99-101. LIANG H Q. Research on the discretization methods for numerical attributes[J]. Information Technology, 2008(5): 99-101. |


