2. 中国石油大学(华东)油气CAE技术研究中心;
3. 中国石油大学(华东)储运与建筑工程学院
2. Oil and Gas CAE Technology Research Center, China University of Petroleum(Huadong);
3. College of Pipeline and Civil Engineering, China University of Petroleum(Huadong)
0 引言
传统油田正朝着智能化方向迈进,作为智能钻井技术中的核心环节,旋转导向钻井技术受到了越来越高的关注。该技术的要素之一即是近钻头处钻井工程参数的实时测量[1],井下工程参数测量短节是实现这一技术的物理载体。设计在近钻头钻铤短节上的传感器可实时、准确地捕获钻头处的钻进工程参数,包括钻压、钻头扭矩及作用于钻头处的弯矩等。此类参数有助于优化钻进及控制井下事故,故随钻参数测量工具及相关技术的研究历来是钻井技术研究中的一项议题[2]。由于恶劣的服役环境及不合理的结构设计,钻具失效事故时有发生[3]。据统计[4],约有14%的油气井发生过钻柱断裂事故,平均每起事故的经济损失超过10.6万美元。从钻井安全角度而言,任何井下工具的设计都应重视其结构的完整性问题。弹性元件作为井下工程参数测量短节的结构薄弱环节,设计中除应使其满足测量性能要求外,还应考虑其结构完整性。
近年来,众多专家对井下工程参数测量技术进行了研究。LIU Y.等[5]提出了井下摩阻力和扭矩的综合动态监测方法,包括基于电阻应变测量技术的新型钻井参数测量仪及相应的参数处理模型。LI C.等[6]为研究井底钻具组合的动力特性,设计了集近钻头力测量及钻柱声传输研究于一体的试验台,研究了使用钻柱作为井下测量数据传输载体的可行性。HU Z.等[7]提出了一种井下工程参数随钻测量系统的设计方案,从硬件布置到软件设计两个层面进行了阐述,并通过现场测试验证了系统的功能及可靠性。上述研究主要侧重于测量技术的整体传感性能或信号传输效率等方面,而针对测量短节中的弹性元件鲜有涉及。樊锐等[8-9]利用LabVIEW对井下工程参数测量短节进行了优化设计,但未考虑弯矩参量,且该方法在涉及到复杂计算时存在一定的困难[10]。
笔者拟对井下工程参数测量短节的弹性元件进行详细研究,通过建立多目标参数优化模型来探讨结构参数设计中测量灵敏度、结构刚度与强度之间的复杂关系,采用在求解复杂系统优化问题上具备更强鲁棒性的遗传算法(NSGA-Ⅱ)获取模型的Pareto最优解;然后对拟定结构进行有限元分析,验证结构的测量性能及强度。所得结果可为近钻头测量短节弹性元件的再优化及后续研究提供参考。
1 弹性元件技术分析 1.1 参数测量的基本原理井下工程参数一般包括钻压、扭矩、弯矩、钻铤外环空压力、钻铤内钻井液压力、加速度及温度等。后4种参数的测量常可直接借助已有的标准传感器,此时仅需关注这些传感器的安装和供电情况。然而,前3个参数的测量通常需要单独设计测量短节的传感部分及转换电路[11-12]。图 1显示了井下工程测量短节的一般结构型式。其中,应变仓外保护筒采用紧定螺钉固定在测量短节本体上,密封方式为动密封,工作时只承受弯矩及环空压力。
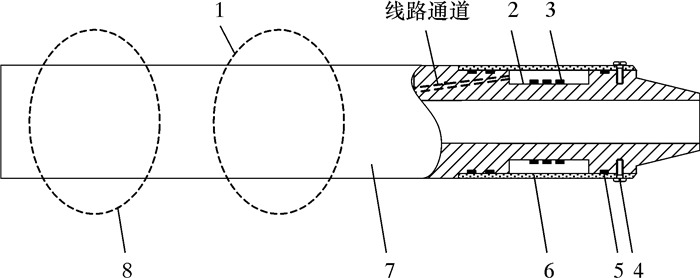
|
| 1—供电装置;2—弹性元件;3—应变片;4—紧定螺钉;5—密封圈;6—应变仓外保护筒;7—短节本体;8—信号处理装置。 图 1 测量短节的一般结构型式 Fig.1 The general structure of the measurement sub |
弹性元件与电阻应变计构成了测量短节的传感部分。测量原理为:附着在弹性元件表面的应变片感知源于钻压、扭矩及弯矩等在弹性元件上引起的弹性变形,实现物理量的机械响应到电阻阻值变化之间的转换;再经测量电路将其转换为电量输出,电量变化的幅度可表征出被测物理量的大小。感应被测物理量的弹性元件是传感器的关键构成。目前存在多种结构型式的弹性元件,旨在适应不同的测量环境以提高测量灵敏度及稳定性[13]。
1.2 弹性元件灵敏度和刚度灵敏度与刚度是弹性元件的两个基本特性。灵敏度是指弹性元件的应变与输入载荷间的比值,计算式为:
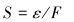
|
(1) |
式中:S为弹性元件灵敏度;F为被测外载;ε为外载作用下传感部位的应变,由于应变值较小,全文均取微应变,即灵敏度是微应变与所测外载的比值。
灵敏度不应以系统终端仪表读数与输入载荷的比值来表征,原因在于它们与仪器的电气放大倍数有关,不能反映弹性元件自身的灵敏度。刚度是指使弹性元件产生单位变形所需施加的外载,其计算公式为:
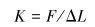
|
(2) |
式中:K为弹性元件刚度,ΔL为外载作用下传感部位的变形量。
弹性元件的刚度直接影响着其传感性能,既包括静态特性方面的灵敏度、线性度及迟滞,也包括动态特性方面的固有频率、频率响应与瞬态响应[13-14]。
测量短节在结构上可被视为一厚壁圆筒,其载荷形式如图 2所示。短节在井下服役时载荷较复杂,此处主要考虑钻压P、钻机驱动力矩T、钻铤短节弯曲力矩M(可分解为Mx、My)及钻铤内外压力pi、po等。由式(1)、式(2)及材料力学相关理论可得弹性元件所测参量的灵敏度及相应刚度的表达式,如表 1所示。
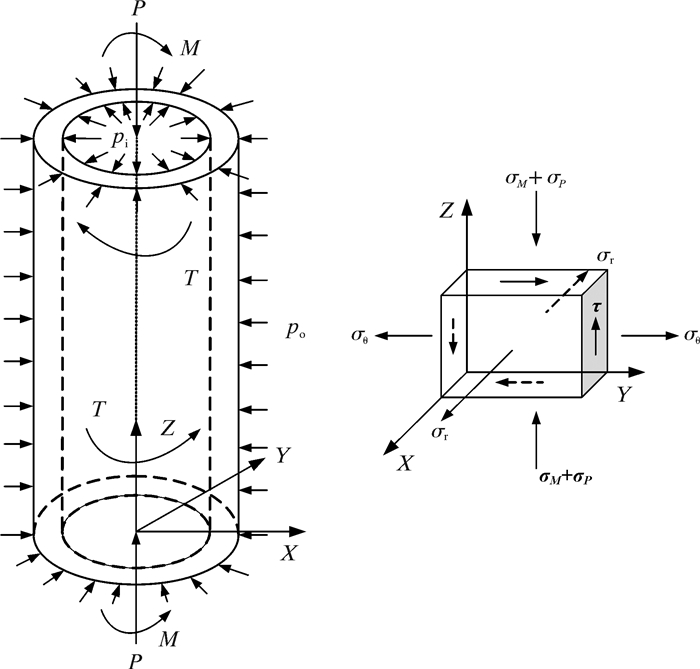
|
| 图 2 测量短节载荷示意图 Fig.2 Schematic diagram of load on measurement sub |
| 项目 | 表达式 |
| 钻压灵敏度SP | 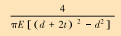 |
| 轴向刚度KP | 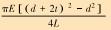 |
| 扭矩灵敏度ST | 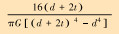 |
| 扭转刚度KT | 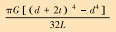 |
| 弯矩灵敏度SM | 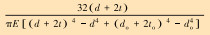 |
| 弯曲刚度KM | 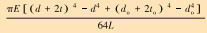 |
表 1中的符号SP、ST、SM分别为钻压灵敏度、扭矩灵敏度和弯矩灵敏度,KP、KT、KM分别为轴向刚度、扭转刚度和弯曲刚度,E、G分别为材料的弹性模量和剪切模量,L、d、t、do、to分别为弹性元件的长度、内径、壁厚及其外保护筒内径与壁厚。
本文所分析的测量短节接头类型为NC38-50,所用材料为42CrMo,服役条件为:最大钻压300 kN,最大扭矩15 kN·m,最大弯矩12 kN·m,最大钻井液压力100 MPa。由表 1可知,决定灵敏度和刚度的结构参数是d、t、L、do及to。为使问题简化,应变仓的外保护筒尺寸根据经验选取,这里暂取do=107 mm,to=10 mm。图 3显示了d、t与各灵敏度和刚度之间的关系。其中:取L=150 mm,参数区间依据经验初选。如图 3a~图 3d所示,随着d和t的增大,灵敏度不断降低,而刚度则呈上升趋势,体现出灵敏度与刚度之间的对立性。而弯矩的测量与钻压和扭矩略微不同,在弯曲力矩作用时,弹性元件与其外保护筒共同承载,因此在弯矩测量灵敏度及弯曲刚度表达式中含有结构叠加成分。总之,各测量参量的灵敏度及其刚度与d、t的取值存在不可调和性及非一致性。另外,L仅与各向刚度有关,且与各刚度值呈负相关。
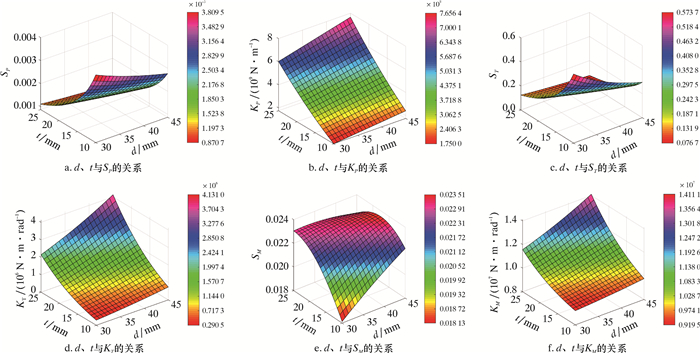
|
| 图 3 参数d、t与灵敏度和刚度之间的关系云图 Fig.3 Relationship between parameters d, t and sensitivity, stiffness |
1.3 弹性元件的结构强度
弹性元件作为测量短节上削薄的一段敏感应变区,是整根短节的危险段。因此,该结构参数的选取不仅要考虑到传感特性,还须兼顾其结构完整性。
由图 2可知,单元体上的应力包括:由钻压P引起的轴向应力σP、弯曲力矩M引起的轴向应力σM,钻盘驱动力矩T引起的切应力τ,短节(钻铤)内压pi、外压po引起的径向应力σr与周向应力σθ。根据材料力学以及弹性力学的相关理论可得到各向应力的表达式[11, 15-16]。由钻压p引起的轴向应力为:
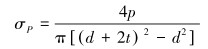
|
(3) |
由弯曲力矩引起的轴向应力为:
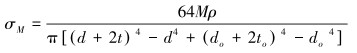
|
(4) |
合成的轴向应力为:
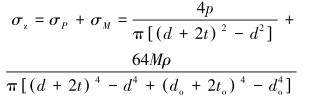
|
(5) |
由扭矩引起的切应力为:
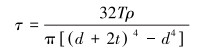
|
(6) |
由拉梅公式得到结构在内、外压作用下的径向应力及周向应力,即有:
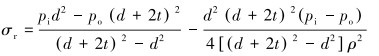
|
(7) |
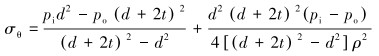
|
(8) |
式中:ρ为截面上任意一点到圆心的距离。
因为切应力为0的微元面就是主平面,主平面上的正应力就是主应力,所以σr为一主应力,故可按平面应力状态来确定另外两个主应力:
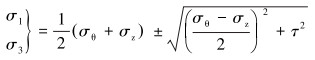
|
(9) |
将式(7)和式(9)带入第四强度理论得到其相当应力,即有:
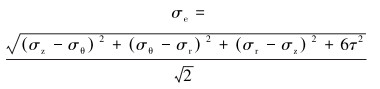
|
(10) |
显然,影响弹性元件传感性能的结构参数d、t也与其强度有关。这就说明弹性元件尺寸参数的选取要同时兼顾结构安全性、各参量测量的灵敏度及各向刚度。由此可见,尽管弹性元件结构简单,但其载荷形式复杂,需满足的指标多。在以往的弹性元件设计中,通常采用反复试凑的方式确定结构尺寸参数,计算繁锁、工作量大,对待该问题,运用数学规划原理来分析不失为一种有效的途径。
2 数学规划模型的建立与求解 2.1 数学规划模型的建立 2.1.1 目标函数分析由于服役环境的特殊性,井下参数测量短节的弹性元件壁厚通常较厚。故在采用电阻应变式电测法进行参数测量时,桥路输出信号比较微弱[17]。同时,为提高系统的抗噪声干扰性能,应适当降低对电气放大倍数的要求,所以在保证结构安全的前提下,应尽可能地提高弹性元件的机械变形量[11]。另一方面,为确保传感器的抗干扰能力,并保持其良好的测量性能,应尽量使弹性元件在载荷作用下的弹性位移减小,这就要求弹性元件具有高的刚度[9, 13-14]。在设计弹性元件时,其灵敏度与刚度之间存在着一定的对立性。原则上各测量参数的灵敏度及各向刚度均应被视为优化模型的目标函数。
2.1.2 灵敏度边界的确定为确保灵敏度设计的可靠性及其与信号后处理系统的匹配性,应统筹考虑弹性元件灵敏度参数的取值,这样可使整个设计更具全局性、科学性。假定传感器的部分特性参数(如量程)、系统供电电压及信号调理系统的一些参数(如供桥电压、增益等)已被初选,据此可计算出测量参数的灵敏度边界[9]。该值应作为上述目标函数的临界下限,如此也可体现出整个设计的弹性。在钻压、扭矩及弯矩的测量中,应变片的布片及组桥方式可采用图 4所示的形式[12, 18-19]。
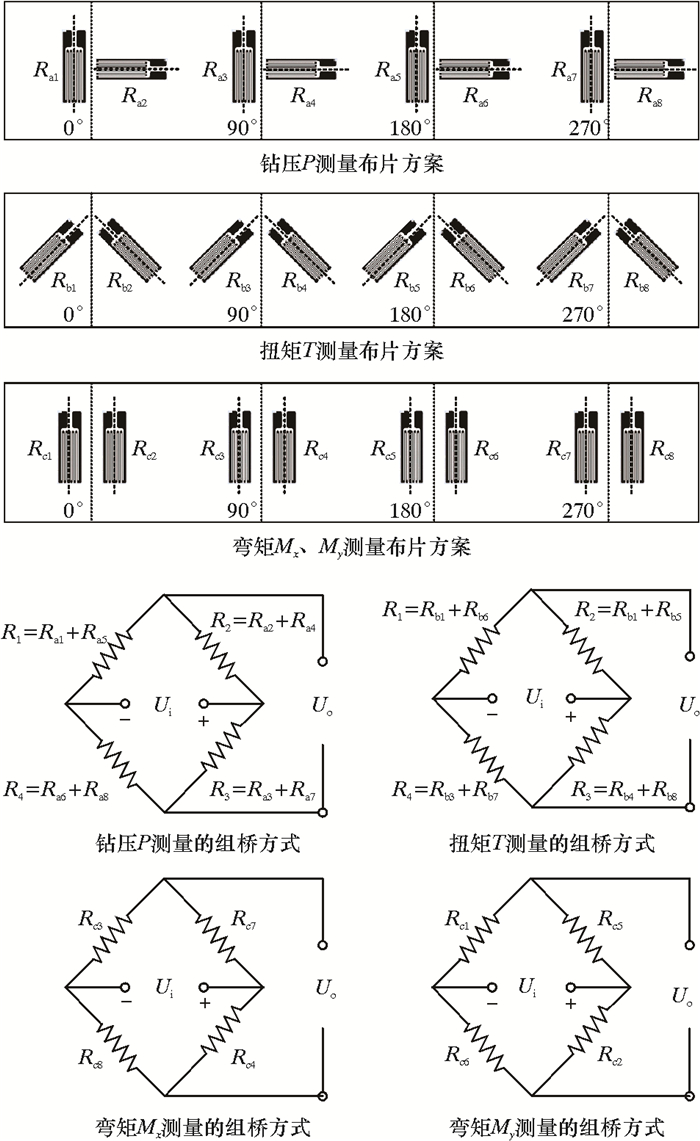
|
| 图 4 布片方案与组桥方式 Fig.4 Distribution and bridge of strain gauge |
相应地,可得各被测参量桥路的输出电压。以钻压测量桥路为例,当钻压、扭矩、弯矩及温度同时影响钻压测量电桥时,式(11)成立。
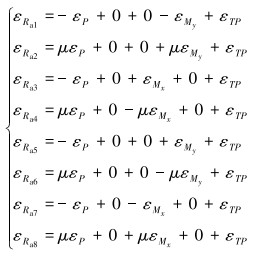
|
(11) |
式中:εRai为应变片Rai的应变量(i=1~8),εP为钻压产生的应变量,εMx、εMy分别为x、y两个方向上弯矩分量产生的应变量,εTP为温度作用产生的应变量,μ为材料的泊松比。
据此,就可得到钻压P测量电桥的输出电压UP的表达式:
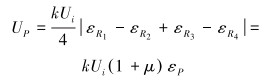
|
(12) |
式中:k为应变计灵敏系数,Ui为供桥电压,εRi为应变计串联后的应变量(i=1~4)。
同理,可得到扭矩及弯矩桥路输出电压:
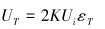
|
(13) |
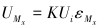
|
(14) |
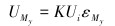
|
(15) |
式中:UT、UMx、UMy分别为扭矩和弯矩测量桥路的输出电压,εT为应变计在驱动力矩T作用下产生的应变量。
由应变与电压输出关联公式[9],可得到各测量参量的灵敏度边界计算公式。
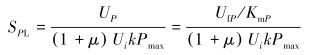
|
(16) |
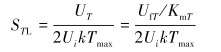
|
(17) |
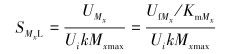
|
(18) |
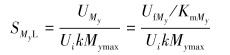
|
(19) |
式中:SPL、STL、SMxL、SMyL分别为钻压、扭矩、弯矩的灵敏度边界,应变计灵敏系数k取2.1;Pmax、Tmax、Mxmax、Mymax分别为各参量的测量量程最大值,这里取Pmax=300 kN、Tmax=15 kN·m、Mmax=12 kN·m;Ui为供桥电压,均取为5 V;UfP、UfT、UfMx、UfMy为各测量参量的最大电压输出,考虑模数转换器的理想情况,均取5 V;KmP、KmT、KmMx、KmMy为各测量参量信号调理电路的增益,均取2 000;材料泊松比μ为0.28。
将初选参数代入式(16)~式(19),可得到各测量参量的灵敏度边界,SPL=7.94×10-4,STL=1.59×10-2,SMxL=SMyL=1.98×10-2。
2.1.3 目标函数与约束条件的确定由1.2节的分析可知,模型的目标函数高达6个,这势必产生较高的计算成本。将一些目标函数合理地转化为约束条件是简化多目标优化问题的一种途径。
根据前文的分析,可将弯矩灵敏度转化为一约束条件。同时由图 3可知,参数d、t对钻压灵敏度和扭矩灵敏度的影响趋势一致,且扭矩灵敏度的裕量(与灵敏度边界的距离)较大,故在两者之中可仅指定钻压灵敏度为目标函数。另外,从图 3还可获知,三向刚度随参数的变化趋势一致,因此仅需选取其中一项作为目标函数。上述分析使得问题模型的目标函数的数量降低为两项,这极大地简化了问题的求解复杂度。
模型的约束条件除含有弯矩灵敏度外,还包括强度要求及结构尺寸上的限制(基于工程现实考虑)。就强度而言,弹性元件作为短节的薄弱环节,应具备足够大的安全系数f。考虑到可能出现的一些极端井况,包括卡钻、遇阻、跳钻及其他未预料到的工况,应适当增大安全余量,这里安全系数f的下限根据工程经验暂定为3,后期可以根据强度校核结果以及现场的实际情况做调整。另外,应变仓外保护筒也与参数d、t相关,故应顾及其强度要求。
外保护筒载荷相对简单,根据工程经验,外保护筒需关注的是密封完整性问题,故选取外保护筒的安全系数fo的下限为1.5。结构尺寸参数在工程或现实角度上的选取原则包括:①结构应有足够大的内径以确保钻井液流动通畅;②弹性元件壁厚不宜过小以适应机械加工要求;③结构在径向上应留出合适的贴片及汇线空间。参数L对模型的影响比较单一,取一个满足布片汇线空间的尽量小值即可。这里根据实际情况及以往经验对变量L赋值,暂取L=150 mm,后续可通过有限元分析来验证。刻画弹性元件结构参数选择问题的非线性优化模型可用式(20)表征。
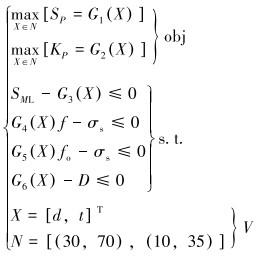
|
(20) |
2.1节所建数学规划模型的求解为一多目标非线性优化问题。该问题在现实世界中具有普遍性,且一般不存在使各目标函数均达到最优的解。传统的多目标优化算法往往在寻优过程中陷入收敛于局部最优的困境。遗传算法是一种搜索启发式算法,其灵感源于查尔斯·达尔文的自然进化理论。该算法具备并行搜索能力,能够自解空间中的多点出发搜索问题的最优解,适合求解多目标优化模型的全局最优解[20]。
NSGA-Ⅱ作为一种带精英策略的非支配排序遗传算法,是当今流行的多目标优化遗传算法之一。因此,本文采用NSGA-Ⅱ算法求解所建数学规划模型。
在仿真计算中,为确保群体的多样性,初始种群规模取40。为避免种群早熟、确保算法收敛,最大进化代数取400。算法中的选择算子采用双支联赛选择。交叉算子采取算数交叉(中间交叉)。变异算子选择高斯变异。在400代进化后将得到模型在其目标域中的Pareto最优解集。
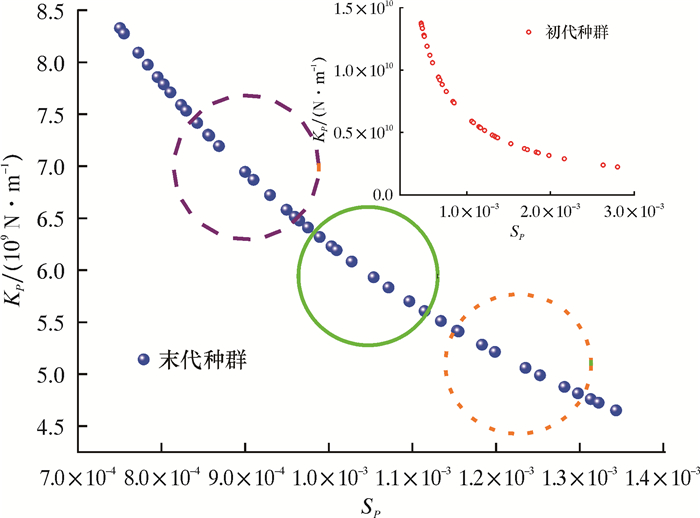
图 5显示出模型在进化过程中的初、末代种群。该问题有一个非凸的Pareto前沿面,反映出两个目标之间的对立性,即不能同时取得各自的最值。
|
| 图 5 模型进化中的初、末代种群 Fig.5 Primary and last generation populations during model evolution |
通常意义上,问题最优解可以取图 5中Pareto曲线上的任意点。基于偏好信息可归结为3种选取策略:①若对钻压灵敏度要求较高,则最优解应在橙色点线范围内选取;②若对轴向刚度要求较高,则应在紫色划线区域选取;③若对2个设计目标没有特殊偏好,则最优解可在绿色实线区域选取。
表 2显示出3种不同偏好策略下的结构参数选择方案及其相应的传感性能与结构强度指标。显然,该优化方法能够为设计人员提供一个直观的有效解数据库。
| 方案 | d/mm | t/mm | L/mm | SP/10-2 | ST/10-2 | SM/10-2 | KP/ (106 N·rad-1) |
KT/ (106 N·m·rad-1) |
KM/ (106 N·m·rad-1) |
σemax/ MPa |
fmin |
| 1 | 32.5 | 30.2 | 150 | 0.081 | 7.90 | 2.24 | 7 770 | 3.67 | 13.0 | 203 | 4.6 |
| 107.0 | 10.0 | — | — | — | — | — | — | — | 516 | 1.8 | |
| 2 | 43.6 | 23.3 | 150 | 0.098 | 9.00 | 2.29 | 6 390 | 3.13 | 12.3 | 248 | 3.8 |
| 107.0 | 10.0 | — | — | — | — | — | — | — | 519 | 1.8 | |
| 3 | 51.2 | 19.4 | 150 | 0.111 | 9.56 | 2.34 | 5 620 | 2.94 | 12.0 | 274 | 3.4 |
| 107.0 | 10.0 | — | — | — | — | — | — | — | 520 | 1.8 |
3 基于有限元法的拟定结构分析
对于前文选定的弹性元件尺寸参数,可进一步通过有限元分析进行相关验算,此处以方案2所定结构为例。测量短节的实际结构比较复杂,而这里主要研究其传感部分,故在建立其有限元模型时做了简化处理。如将两端的螺纹简化为锥形面,且暂不考虑短节上的其他结构特征。至于边界条件,下部端面设置为约束端,上端为钻压、扭矩及弯矩的加载部位,短节承受的内、外压均匀施加在模型的内、外壁上。
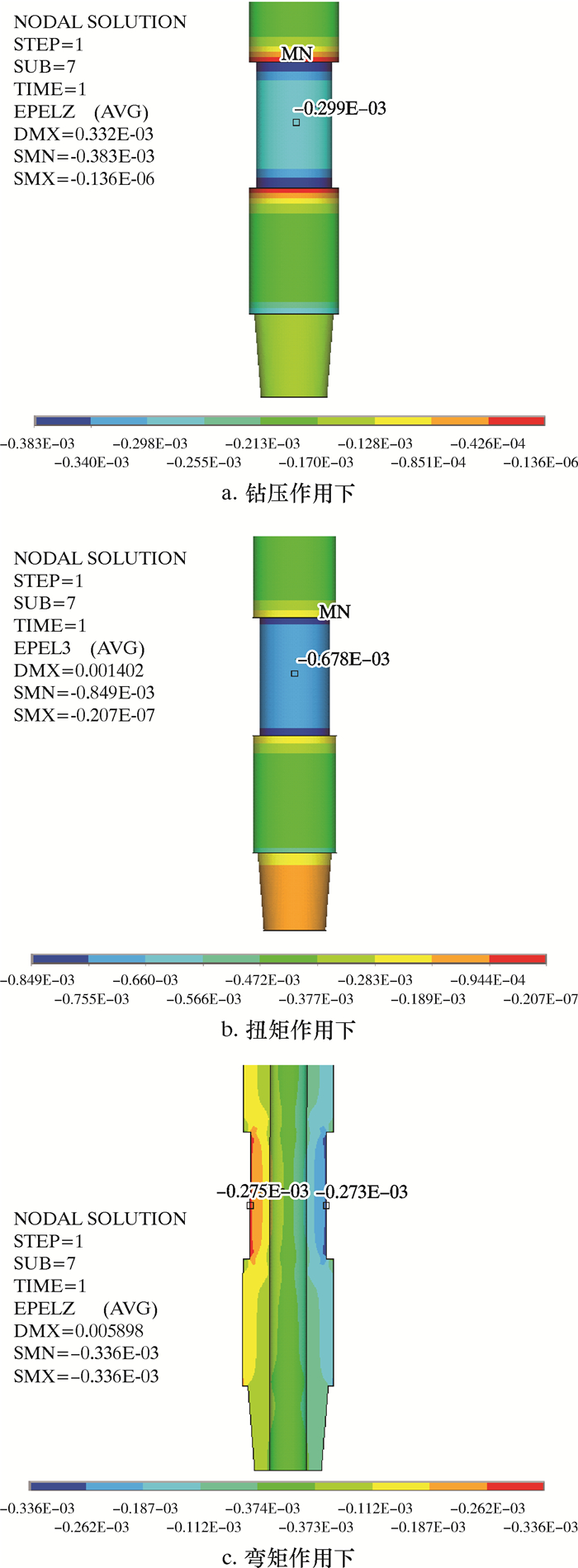
分别分析了模型在钻压、扭矩、弯矩作用下弹性元件的应变分布情况,结果如图 6所示。根据式(3)、式(4)、式(6)及胡克定律,可求得结构在单独钻压、扭矩及弯矩作用下的应变,分别为-2.93×10-4、-1.35×10-3 (与第三主应变为2倍关系)、-2.75×10-4。弹性元件测量区域的应变值与理论值相比误差在3%以内,具有较好的一致性,验证了结构测量性能的可靠性。从图 6可以看出,在测量区的两端均存在应力过渡区。其中,钻压作用下的应力过渡区域最大,两端约为20 mm。为消除边界效应的影响,在粘贴应变片时,应避开此区域。本研究前面所选用的150 mm长的测量区域可满足贴片工艺需求,是一个合适的取值。
|
| 图 6 各被测参量作用下弹性元件的应变分布 Fig.6 Strain distribution of elastic cell under the measured parameters |
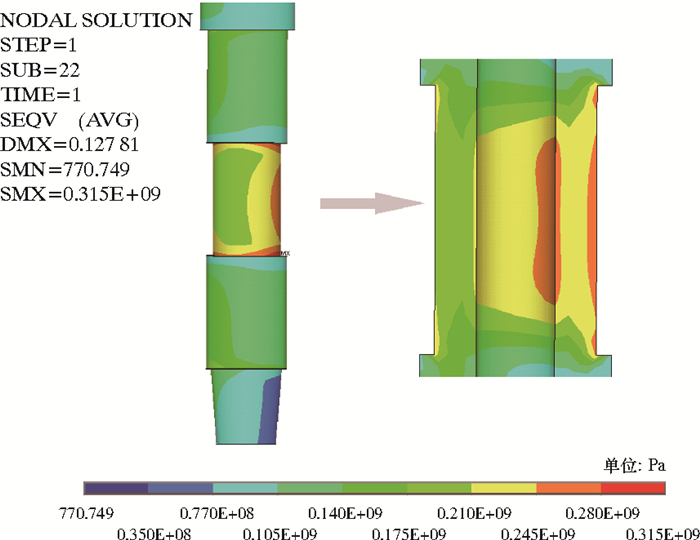
为确保弹性元件在极端测量工况下的结构完整性,对其在各测量参量取量程最大值、且承受最高钻井液压力作用时的状态进行有限元分析。为简化模型,在分析时未包含应变仓外保护筒。图 7为极端测量工况下弹性元件的应力云图。由图 7可知,测量区的最大Mises等效应力约为260 MPa,与理论值相近,满足强度条件。另外,由图 7还可看出,最大Mises等效应力出现在测量区两端过渡台阶夹角位置,实际加工中可通过设置圆角等措施予以缓解。
|
| 图 7 极端测量工况下弹性元件的应力分布 Fig.7 Stress distribution of elastic cell under extreme measurement conditions |
4 结论及展望
(1) 将弹性元件结构参数取值过程中存在于灵敏度、刚度与强度之间的复杂关系抽象为一多目标优化数学模型。
(2) 采用非支配排序遗传算法NSGA-Ⅱ求解了上述多目标优化问题,优化结果可为设计人员提供一个弹性的参数取值数据库。
(3) 基于有限元法对拟定结构进行了测量性能验证及结构强度验证,以期使整个设计更加趋于严谨。
综上所述,所提出的研究方法可在一定程度上确保测量短节弹性元件的综合性能。在建立数学模型时进行了一些简化,这有待后续研究的完善。本文的研究方法可推广至其他结构型式或其他领域传感器弹性元件的设计中。
| [1] |
ZHANG C, ZOU W, CHENG N B. Overview of rotary steerable system and its control methods[C]//2016 IEEE International Conference on Mechatronics and Automation. Harbin: IEEE, 2016: 1559-1565.
|
| [2] |
MA T S, CHEN P. Development and use of a downhole system for measuring drilling engineering parameters[J]. Chemistry and Technology of Fuels and Oils, 2015, 51(3): 294-307. DOI:10.1007/s10553-015-0603-z |
| [3] |
ZAMANI S M, HASSANZADEH-TABRIZI S A, SHARIFI H. Failure analysis of drill pipe:a review[J]. Engineering Failure Analysis, 2016, 59(1): 605-623. |
| [4] |
LIN Y H, QI X, ZHU D J, et al. Failure analysis and appropriate design of drill pipe upset transition area[J]. Engineering Failure Analysis, 2013, 31(7): 255-267. |
| [5] |
LIU Y, MA T S, CHEN P, et al. Method and apparatus for monitoring of downhole dynamic drag and torque of drill-string in horizontal wells[J]. Journal of Petroleum Science and Engineering, 2018, 164: 320-332. DOI:10.1016/j.petrol.2018.01.077 |
| [6] |
LI C, DING T H, WANG P. An experimental rig for near-bit force measurement and drillstring acoustic transmission of BHA[J]. Measurement, 2011, 44(4): 642-652. DOI:10.1016/j.measurement.2010.12.005 |
| [7] |
HU Z, XIE X H, GE L, et al. Research on the system of down-hole engineering parameters measure while drilling[J]. Open Petroleum Engineering Journal, 2014, 7: 149-153. DOI:10.2174/1874834101407010149 |
| [8] |
樊锐, 谢赛. 近钻头钻压、扭矩测量短节的结构参数设计[J]. 石油机械, 2010, 38(7): 17-19. FAN R, XIE S. Design of the structural parameter of the near-bit drilling pressure and torque's measurement sub[J]. China Petroleum Machinery, 2010, 38(7): 17-19. |
| [9] |
罗君.井下工程参数测量短节的研制[D].北京: 北京航空航天大学, 2008. LUO J. Research on apparatus used for measurement of engineering parameters in well drilling[D]. Beijing: Beihang University, 2008. |
| [10] |
王肖隆, 王富丽, 张肖垒, 等. 超宽带亚周期微波脉冲实时时频分析系统[J]. 浙江工业大学学报, 2019, 47(2): 175-179. WANG X L, WANG F L, ZHANG X L, et al. Real-time time-frequency analysis system for ultra-wideband sub-cycle microwave pulse[J]. Journal of Zhejiang University of Technology, 2019, 47(2): 175-179. DOI:10.3969/j.issn.1006-4303.2019.02.011 |
| [11] |
耿艳峰, 张海花, 华陈权, 等. 近钻头工程参数测量短接结构设计与误差分析[J]. 电子测量与仪器学报, 2010, 24(5): 454-459. GENG Y F, ZHANG H H, HUA C Q, et al. Structural design and error analysis of a device for measuring drilling engineering parameters near the bit[J]. Journal of Electronic Measurement and Instrument, 2010, 24(5): 454-459. |
| [12] |
耿艳峰, 杨锦舟, 闫振来, 等. 基于电阻式应变片的近钻头工程参数测量技术研究[J]. 传感技术学报, 2008, 21(6): 1084-1088. GENG Y F, YANG J Z, YAN Z L, et al. Measurement techniques for drilling engineering parameters near the bit based on resistance strain gauges[J]. Chinese Journal of Sensors and Actuators, 2008, 21(6): 1084-1088. DOI:10.3969/j.issn.1004-1699.2008.06.041 |
| [13] |
计欣华, 邓宗白, 鲁阳, 等. 工程实验力学[M]. 2版. 北京: 机械工业出版社, 2010. JI X H, DENG Z B, LU Y, et al. Engineering experimental mechanics[M]. 2nd ed. Beijing: China Machine Press, 2010. |
| [14] |
孙永华.高频响三维动态铣削力测试平台设计与试验研究[D].南京: 南京航空航天大学, 2012. SUN Y H. A design of high frequency three-dimensional dynamometer and experimental study for high speed milling[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. |
| [15] |
GROSS D, EHLERS W, WRIGGERS P, et al. Mechanics of materials-formulas and problems[M].[S.l.]: Springer Nature, 2017.
|
| [16] |
BYROM T G. Casing and liners for drilling and completion:design and application[M]. 2nd ed. Amsterdam: Elsevier, 2014.
|
| [17] |
王银生, 杨锦舟, 韩来聚, 等. 近钻头钻压、扭矩测量中微弱信号处理[J]. 石油钻探技术, 2009, 37(4): 73-75. WANG Y S, YANG J Z, HAN L J, et al. Signal processing of near-bit weight on bit and torque[J]. Petroleum Drilling Techniques, 2009, 37(4): 73-75. DOI:10.3969/j.issn.1001-0890.2009.04.019 |
| [18] |
DENISON E B. Steering drill string: 4324297[P]. 1982-04-13.
|
| [19] |
胡泽, 肖宇恒, 葛亮, 等. 应变式井下工程参数测量传感器组桥与布片研究[J]. 自动化仪表, 2012, 33(5): 77-79. HU Z, XIAO Y H, GE L, et al. Research on the bridging and arranging of strain sensors for measuring the engineering parameters down the pit[J]. Process Automation Instrumentation, 2012, 33(5): 77-79. DOI:10.3969/j.issn.1000-0380.2012.05.023 |
| [20] |
WANG B H, LIANG Y T, ZHENG T C, et al. Multi-objective site selection optimization of the gas-gathering station using NSGA-Ⅱ[J]. Process Safety and Environmental Protection, 2018, 119: 350-359. DOI:10.1016/j.psep.2018.08.017 |



