2. 长江大学非常规油气湖北省协同创新中心
2. Hubei Cooperative Innovation Center of Unconventional Oil and Gas, Yangtze University
0 引言
行星齿轮传动在机械行业中应用广泛,起重机械、工程机械、冶金机械、建筑机械、石油机械、纺织机械、机床、汽车、飞机和船舶等均采用了行星齿轮传动[1]。行星架作为整个机构的动力输出端零件,其承受的载荷最大。行星架与行星轮轴装配时多采用过盈连接方式,这是一种名义上静止的配合形式。行星轮系常受到各种内外部激励的影响,如环境因素或齿轮啮合冲击激励及时变的刚度激励而产生振动,导致行星架轴孔过盈连接处出现微米级的相对滑移,最终引起接触面之间的微动磨损。当磨损积累到一定程度时,会造成行星架左右侧板与筋柱的撕裂及太阳轮行星轮打齿的现象,从而破坏行星齿轮减速系统。
微动磨损是引起机械部件损坏的重要因素[2]。英国学者J.F.ARCHARD[3]提出了著名的Archard磨损理论模型;R.D.MINDLIN[4]通过对接触表面的应力分布进行理论分析计算,认为接触对之间的接触状态是配合面之间切应力与摩擦力相互竞争的结果,接触表面之间的接触状态分为滑移区和非滑移区。周仲荣等[5-7]的研究表明,导致磨损的两个关键因素是接触表面的摩擦力与相对滑移距离。工程技术人员可以通过微动疲劳/微动磨损试验机进行大量试验,获得微动磨损的基本参量(如正压力及接触对之间相对滑移幅值等)对接触对表面微动损伤的影响。然而对于过盈配合形式结构的包容面与被包容面之间的几何特征,很难通过试验机测得微动磨损的正压力以及接触对之间相对滑移的幅值。
为了弥补上述不足,将有限元法应用于微动磨损研究[8-11]。P.A.MCVEIGH等[12]建立了微动疲劳的有限元模型,分析了接触载荷、摩擦因数和接触对之间的切向力等因素对铝合金材料裂纹扩展规律的影响。宫昱滨等[13]以空心轴过盈结构为研究对象,基于Archard的磨损计算模型,通过有限元分析得到了接触压力、摩擦切应力和滑移距离等影响微动磨损的主要因素的变化规律。李玲等[14]以柱面/平面结构为研究对象,揭示了不同加载幅值时危险加载条件的变化规律。
仿真研究对象多是单一圆柱形式的微动磨损结构,在分析时将单一构件模型简化为二维平面问题[15-16],而忽略了装配体中其他构件的影响。因此,本文以行星架轴孔过盈连接处的微动磨损为研究对象,考虑了齿轮啮合冲击与时变的刚度激励对于磨损的影响,以ANSYS软件为分析手段,采用网格划分技术研究网格敏感性对微动磨损有限元分析的影响;同时编写APDL程序对有限元分析结果进行数据提取,得到过盈配合表面上各节点的应力和滑移状态分布,并基于Archard模型的离散化深度磨损修正计算方法,得到过盈配合面上的微动磨损分布规律,预测过盈配合面上微动磨损的危险位置。
1 离散化深度磨损修正计算方法英国Leicester大学工程系教授Archard于1953年提出了著名的粘着磨损理论计算模型:
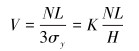
|
(1) |
式中:V为接触表面的磨损体积,N为接触表面的法向载荷,σy为接触表面的屈服极限,H为布氏硬度,L为两接触表面之间的相对滑移距离,K为磨损系数。
Archard理论模型阐述了单位时间内发生相对滑移过程中接触对表面的磨损量ΔV的计算方法。在Archard模型中N通常被近似地看作为一个常数,相对滑移距离L为可测定的参数,总体磨损量V是单位磨损量ΔV在时间上的积累。但在实际磨损过程中,考虑到内、外部激励对接触表面应力以及滑移分布的影响,各节点的微动磨损相关参量是随时间变化的函数,原有的Archard模型已不再适用。随着有限元仿真技术的发展,通过有限元仿真模拟磨损过程,可以得到接触面上微动参量的分布。因此,为了寻求精度更高的计算模型,需要对Archard模型进行修正。考虑到单位时间内磨损体积是表面法向磨损速度在相对滑移表面上的时间积分,则有:
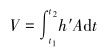
|
(2) |
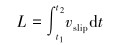
|
(3) |
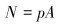
|
(4) |
式中:h′为沿表面法向的磨损速度,m/s;A为接触对的相对滑移面积,m2;vslip为接触对之间的相对滑移速度,m/s;p为接触面上的法向应力,Pa。
将式(2)~式(4)带入式(1)可得:
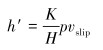
|
(5) |
对时间积分,即可获得某节点磨损表面的磨损深度计算模型:
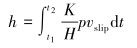
|
(6) |
行星齿轮传动系统有多个啮合副、多处过盈配合连接,是一个较复杂的非线性系统。本文基于SolidWorks软件搭建行星轮系的几何模型(见图 1)。
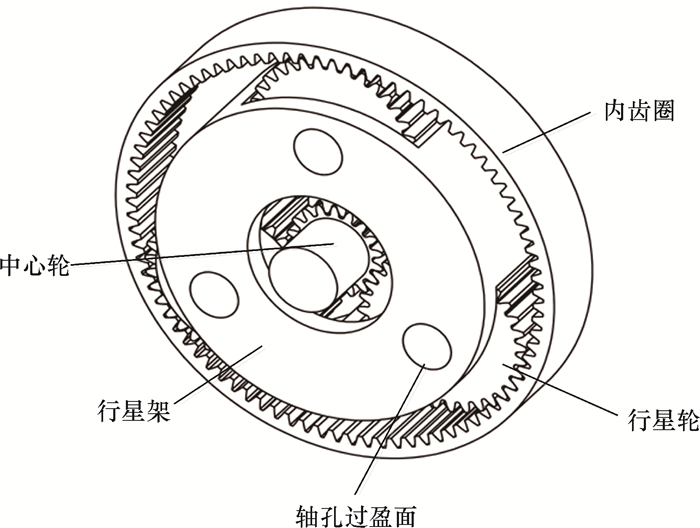
|
| 图 1 行星轮系几何模型 Fig.1 Planetary gear geometry model |
在对行星架轴孔处的微动磨损进行分析时,由于整体模型结构较复杂,涉及到的单元节点数量庞大,占用较大的计算机资源,所以对整个磨损过程进行分析不现实。考虑到在一段时间内接触表面的形貌特征变迁对啮合的接触状态及磨损的影响很小,计算行星轮系统转动一个啮合周期时的磨损深度,并将其作为行星架轴孔接触表面的磨损评价标准。齿轮啮合周期的计算公式如下:
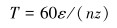
|
(7) |
式中:T为啮合周期,s;ε为重合度,无量纲;n为中心轮转速,r/min;z为中心轮齿数。
中心轮与行星轮重合度ε=1.602,太阳轮转速n=568.7 r/min,太阳轮齿数z=18。通过计算得到该级行星轮的啮合周期T=0.060 96 s,该周期内太阳轮转动的角度为32°。
行星轮各部件参数为:中心轮齿数18,行星轮齿数33,内齿圈齿数84,行星轮个数3,模数12,齿宽180,传动比5.67。
2.2 有限元模型前处理将几何模型导入ANSYS Workbench软件,对行星轮系的有限元模型进行合理简化。根据圣维南原理,其边界条件的设置区域离行星轮系轴孔处接触区域的距离较远,单独对一对行星轮与太阳轮区域进行分析将不会影响分析结果。由于3个行星轮绕太阳轮呈周期性对称分布,所以本模型仅取一对行星轮与太阳轮对应的行星架轴孔过盈面进行分析,模型简化方式如下。
(1) 原有的螺栓连接等效为刚性连接。
(2) 去掉行星轮系结构上一些不必要的倒角、圆角和圆孔等特征。
根据行星轮系运行工况,分别将行星架与机架、太阳轮与机架支撑面设置Body-Ground类型的转动副,约束径向和轴向位移,释放其周向转动自由度;将行星轮轴与行星轮设置为Body-Body转动以保证行星轮绕着太阳轮公转和行星轮轴自转;行星轮轴与行星架之间设置为过盈接触,并设置摩擦因数和过盈量等相关参数;各齿轮副之间设置为无摩擦接触。各部件的材料属性如表 1所示。
| 名称 | 材料 | 弹性模量/GPa | 泊松比 | 屈服强度/MPa | 密度/ (g·cm-3) |
| 输入轴 | 42CrMo | 212 | 0.280 | 930 | 7.85 |
| 行星架 | 35CrMo | 213 | 0.286 | 835 | 7.87 |
| 太阳轮 | 17CrNiMo6 | 22 | 0.260 | 900 | 7.87 |
| 行星轮 | 17CrNiMo6 | 22 | 0.260 | 900 | 7.87 |
| 齿圈 | 30Cr2Ni2Mo | 209 | 0.300 | 590 | 7.85 |
完整的行星轮系所承受的扭矩T′=580.0 kN·m。取一对行星轮与太阳轮啮合进行分析,则其所受扭矩为T′/3=193.3 kN·m。在行星架上施加负载转矩,太阳轮上设置一个啮合周期的转动角度,并设置时间步长等参数。行星轮系有限元模型如图 2所示。
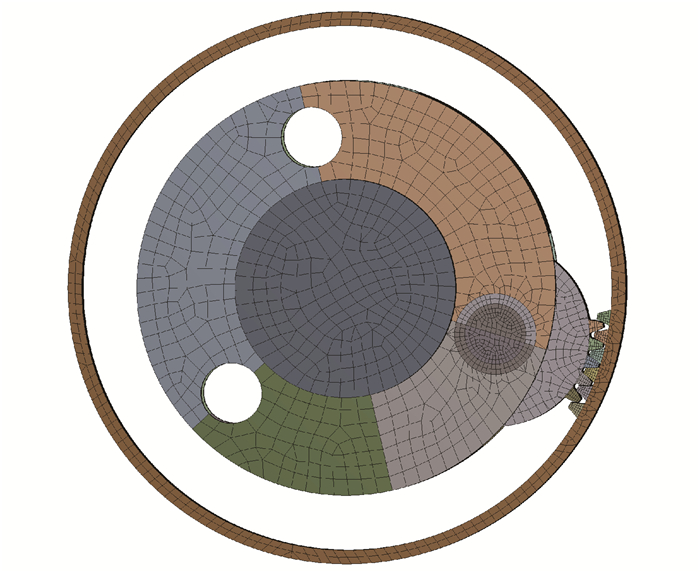
|
| 图 2 行星轮系有限元模型 Fig.2 Finite element model of the planetary gear train |
2.3 网格敏感性研究
对于过盈接触表面的磨损问题进行有限元分析时,接触表面的网格质量直接决定分析结果的准确性。相对滑移速度是微动磨损研究过程中的关键参量,因此通过分析网格单元密度对于相对滑移速度误差的影响,来研究网格敏感性对于误差的影响。在对网格进行划分时保证接触对目标面与接触面之间的节点一一对应,如图 3所示。
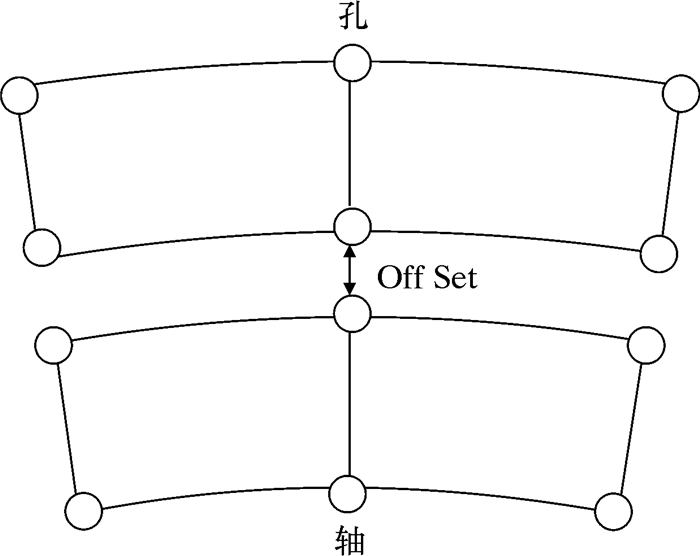
|
| 图 3 接触表面节点分布 Fig.3 Contact surface node distribution |
考虑到行星架轴孔接触对的误差主要来源于不规则几何模型的离散化误差,而这种误差主要集中在不规整的非线性几何形状表面,因此轴孔过盈面的误差主要来源于圆柱表面的周向方向,而圆柱表面的轴向为线性变化,其对误差的影响可以忽略不计。对于不同密度的网格,均将行星架轴孔处接触对的网格沿轴向均分为10等份,而通过控制周向网格的份数来控制每组网格的密度。分别沿周向将网格划分为20、30、40、50和60等份共5组,如表 2所示。
| 网格精度等级 | Mesh1 | Mesh2 | Mesh3 | Mesh4 | Mesh5 |
| 单元数量 | 200 | 300 | 400 | 500 | 600 |
| 单元尺寸 | 34 | 23 | 17 | 13 | 11 |
选同一几何位置的节点作为研究对象,在分析计算时,将后一组的Mesh(n+1)下的节点解作为精度计算时的基准解,而将Mesh(n)作为误差计算的对象。提取在时间历程下的速度vm和 vm+1,将新基准看作无误差的约定准确值,则相对误差为:
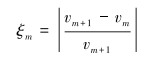
|
(8) |
以此计算出不同网格精度Mesh(n)等级下各载荷子步滑移速度相对误差ξm,如图 4所示。
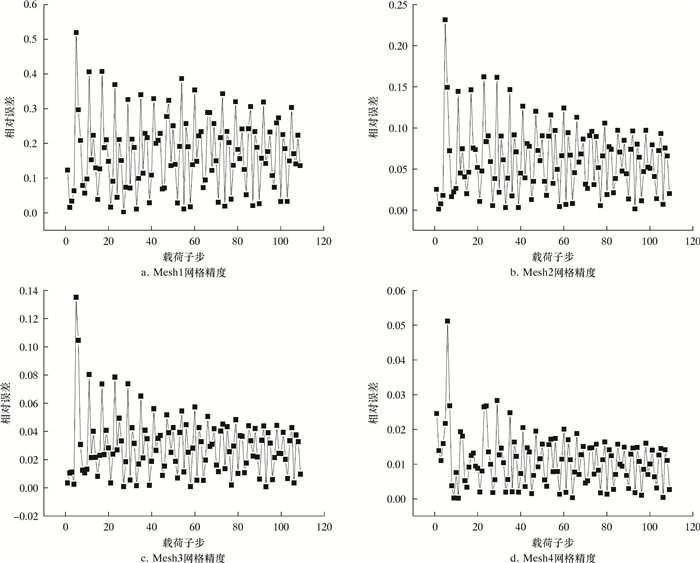
|
| 图 4 各载荷子步滑移速度相对误差 Fig.4 Relative slip speed error of each load sub-step |
图 5为有限元分析载荷步下相对滑移速度平均误差随网格精度的变化曲线。由图 5可知,在对过盈面进行瞬态动力学分析时,非线性变化几何形状表面的离散化误差对有限元的计算精度影响较大,轴孔处过盈接触表面相对滑移速度的平均误差ξ随网格密度的增加而减小。因此,为了保证较高的计算精度、较快的收敛速度及后处理计算效率,不宜选网格数量过大或过小的有限元分析模型。当行星架轴孔过盈微动磨损计算模型网格数量为500时,ξ=0.016,此时几何表面形状的离散化误差可以忽略。因此,选取网格数量500对本算例进行分析研究。
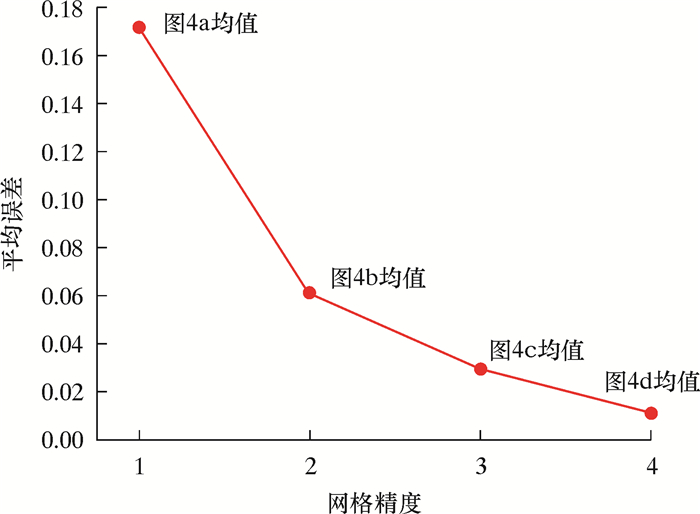
|
| 图 5 相对滑移速度平均误差 Fig.5 Average relative slip speed error |
3 行星架轴孔处微动磨损危险点预测 3.1 微动摩擦接触状态分析
关于接触对目标面与接触面之间的接触状态,学者MINDLN认为接触状态是两接触表面之间的切应力q与表面摩擦力相互竞争的结果。接触对表面接触状态的判定关系为:
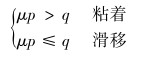
|
(9) |
式中:p为接触表面的正压力,μ为接触表面的摩擦因数。
提取输出端一侧过盈配合面节点的数据,利用MATLAB可以得到过盈配合面的正应力分布。图 6为过盈配合面上节点的应力云图。从图 6可见,靠近行星架轴孔内侧区域的应力集中较为明显。这是因为接触边缘存在应力奇异性且行星轴在转动过程中需要平衡行星轮与太阳轮及内齿圈的啮合力,所以会承受弯矩作用。又由于行星轴为弹性元件,所以在靠近行星架轴孔内侧的部分更容易产生应力集中,而内侧接触面的材料及几何结构的不连续也加剧了这种应力集中现象。
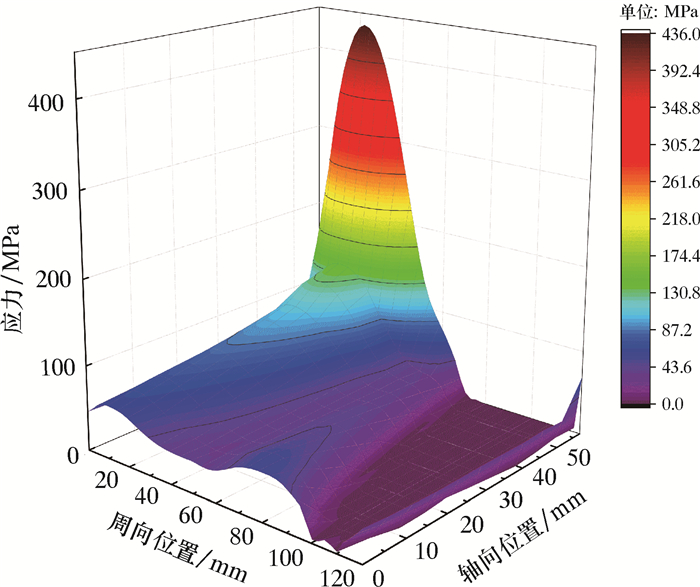
|
| 图 6 过盈配合面上节点的应力云图 Fig.6 Stress distribution of the interference fit surface |
图 7为行星轮系稳定运行后,某载荷子步下行星架过盈面周向和轴向应力分布图。
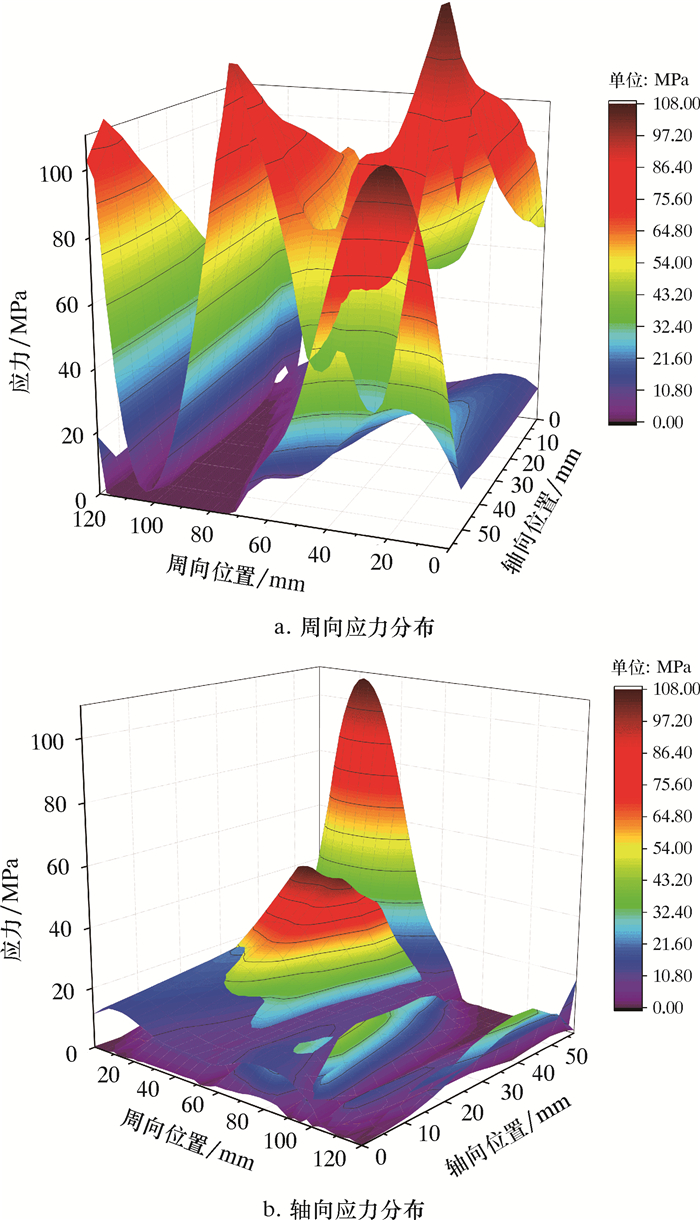
|
| 图 7 过盈配合面应力分布图 Fig.7 Stress distribution of the interference fit surface |
由接触状态的应力对应关系可知:在过盈面周向方向上接触状态以滑移为主,仅靠近轴孔内侧存在小部分粘着区域;在过盈面轴向方向上摩擦力与切应力在多个面上出现互相交织的情况,整个表面的接触状态以混合区为主。
3.2 微动损伤位置预测 3.2.1 磨损深度的离散化计算方法在有限元分析计算中,由于接触点的相对滑动速度vslip随时间的变化曲线比较复杂,所以对式(6)的求解很困难。为了简化计算过程,在行星架轴孔的微动磨损深度计算时,采用一种离散化的插值计算方法:将一个啮合周期T均分为有限个时间段,每段时间间隔为ti+1-ti=Δt=T/m,当分段数m足够大时,可以认为在较小的Δt时间间隔内,vslip随时间呈线性变化。令x=t, y=L,以线性的方式去拟合非线性曲线,结果如图 8所示。
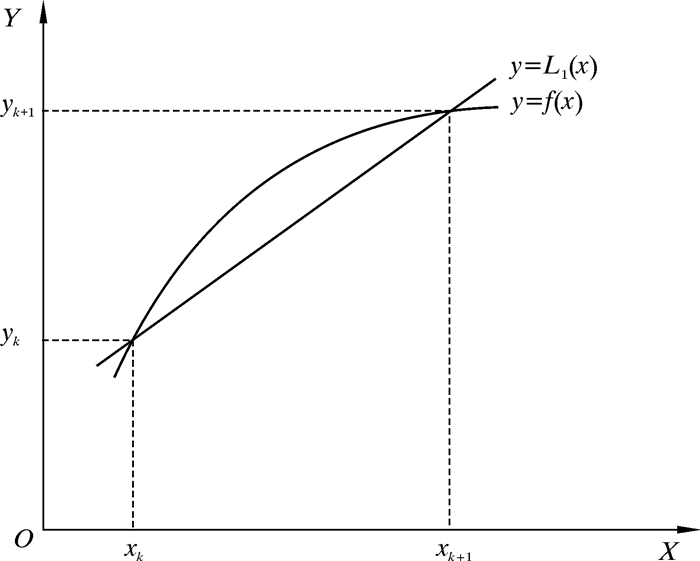
|
| 图 8 离散化原理图 Fig.8 Discretization schematic |
假设在某段已知区间[xk, xk+1]端点处的函数值yk=f(xk), yk+1=f(xk+1), 要求线性的插值函数多项式L1(x)满足:
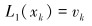
|
(10) |
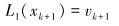
|
(11) |
多项式L1(x)的表达式可以由几何意义给出,即有:
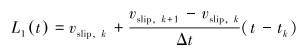
|
(12) |
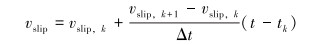
|
(13) |
节点处的正应力为:
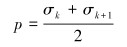
|
(14) |
将式(14)带入式(6)即可求得在时间[t1, t2]内磨损深度积累量hk的表达式:
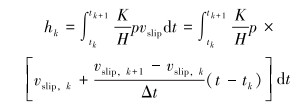
|
(15) |
某节点处的磨损深度h在时间t内的积累可以表示为:
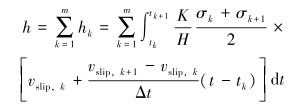
|
(16) |
式中:m为有限元分析计算中总的增量步数;σk、σk+1分别为某节点在第k和k+1个增量步下对应的接触表面正压力。
3.2.2 行星架轴孔过盈配合面磨损深度分布过盈配合表面行星架轴孔与行星轮轴节点的滑移速度分别为vk与vz,则相对滑移速度vslip=vk-vz。在一个增量步下,分别提取tk、tk+1时刻下某对节点的相对滑移速度与行星架轴孔处对应节点的正压力σk、σk+1。将提取的数据带入式(15)即可得到该节点在一个增量步对应时间间隔下的磨损深度,其中磨损系数K=1×10-4[17]。通过式(15)对每个时间增量步在式(14)下的结果求和,得到一个啮合周期内行星架轴孔处该节点的磨损深度积累量。采用同样的方法,利用APDL语言及MATLAB工具对整个过盈配合面的节点数据进行批处理,即可得到行星架轴孔过盈配合表面各节点的磨损深度分布,如图 9所示。
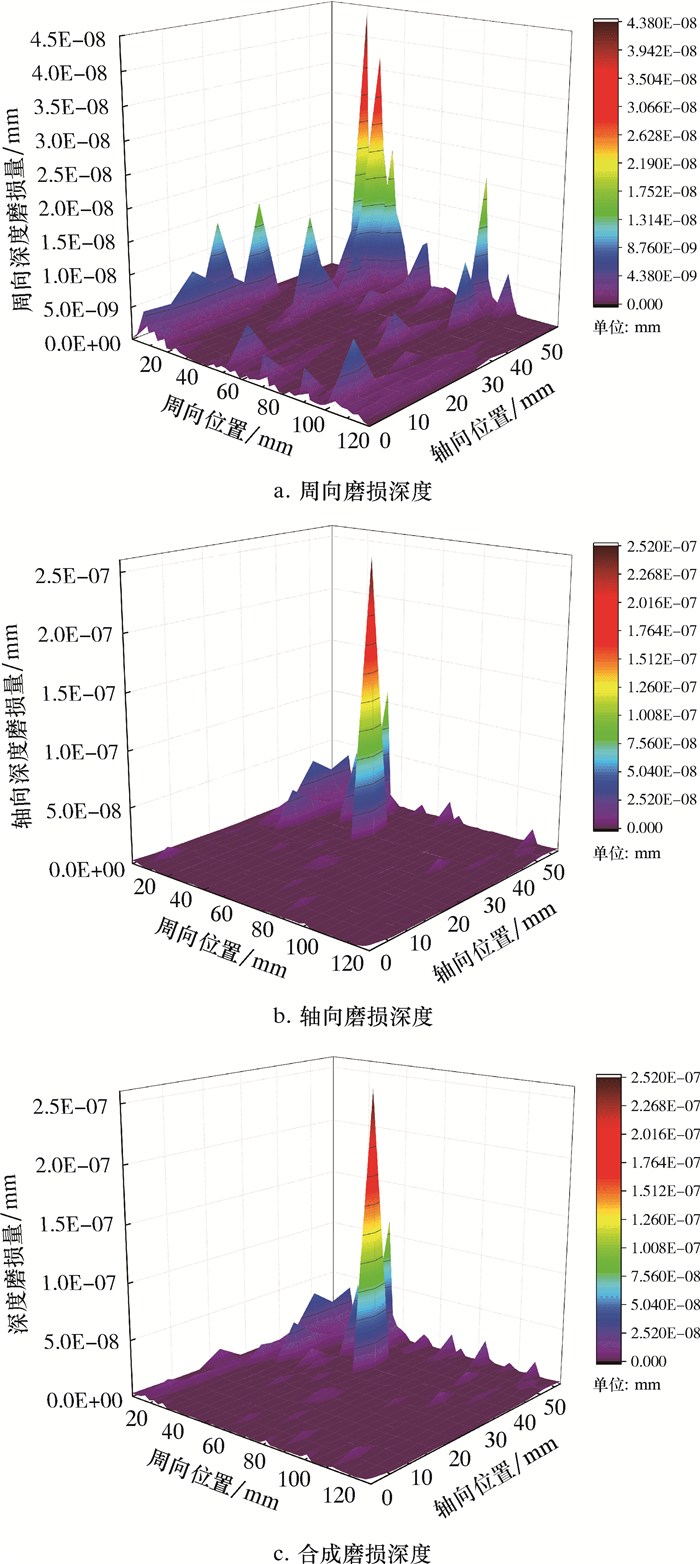
|
| 图 9 过盈配合面微动磨损分布 Fig.9 Fretting wear distribution of interference fit surface |
由图 9a可知接触表面周向的微动磨损对于整体的影响较小。由图 9b可知接触表面轴向的微动磨损远大于周向的磨损量,是引起行星架轴孔处微动磨损的主要因素。微动磨损主要集中在展开的平面轴向40~50 mm、周向0~40 mm区域。该区域位于内侧的接触边缘,在远离该区域的部位磨损量逐渐减小,最终达到相对均匀的磨损状态。引起这种情况的主要原因在于行星架轴孔处轴向过盈表面的接触状态以混合区为主,该区域存在较大的摩擦力和较强的表面塑性,整体的运行机理十分复杂,是磨损与裂纹萌生的危险区域;而行星架轴孔周向接触表面的接触状态以滑移区为主,远离了危险区,整体的磨损量较小。行星架轴孔过盈配合面不论是周向还是轴向上微动磨损危险位置均出现在行星架轴孔过盈面接触边缘的混合区域。
3.3 摩擦因数对轴孔过盈面微动磨损影响摩擦因数是影响轴孔处微动磨损的关键因素。将过盈配合面各节点的磨损量取平均值,并以此为标准衡量配合面的磨损情况。过盈量为0.03 mm时行星架轴孔过盈面深度平均磨损量随摩擦因数的变化规律如图 10所示。当摩擦因数在0.1~0.3之间变化时,周向和轴向平均磨损深度随摩擦因数的增大而减小,轴向磨损深度大于周向磨损深度,是影响微动磨损深度的主要因素。在周向上,当摩擦因数达到0.2后,增大摩擦因数对周向的平均磨损量影响不大。产生这种现象的主要原因是:当摩擦因数增大时,过盈接触表面轴向上的接触状态发生改变,由原先的混合区向粘着区过渡,摩擦因数的增大使得过盈接触表面更多地远离了微动磨损的危险区域,磨损量也随之减小;而在周向上由于剪切应力远大于摩擦力,在一定程度上增大摩擦因数并没有改变过盈面的接触状态,因此对于微动磨损深度的影响不大。
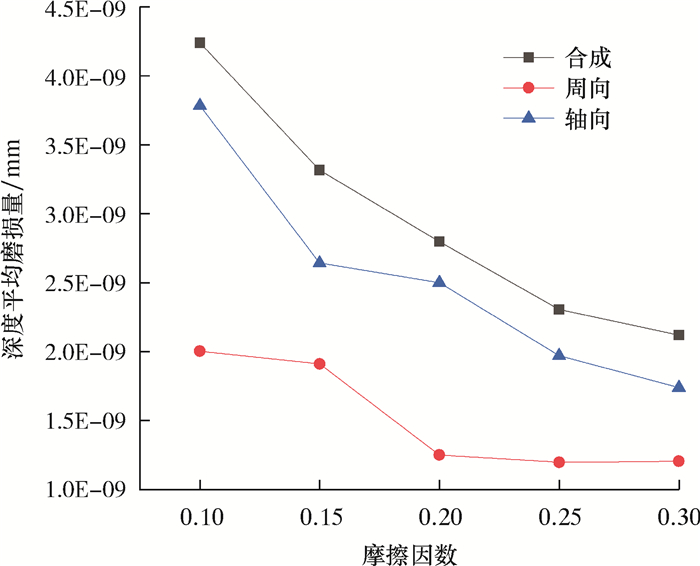
|
| 图 10 磨损深度随摩擦因数的变化曲线 Fig.10 Wear depth as a function of friction factor |
4 结论
(1) 基于Archard理论磨损计算模型,结合有限元技术,提出了适用于行星架轴孔过盈配合面的离散化深度磨损修正计算方法。
(2) 在对含有几何非线性特征的接触面进行微动磨损有限元分析时,应考虑模型的离散化误差对计算结果的影响。在行星架轴孔过盈面磨损深度算例中,当网格数量为500时,既保证了收敛速度,同时又提高了有限元计算的准确性。
(3) 行星架轴孔过盈面的微动磨损主要发生在接触面的轴向上,混合区域是微动磨损发生的危险区域,其中行星架轴孔内侧磨损情况最严重。当摩擦因数在0.1~0.3区间时,周向的微动磨损对摩擦因数并不敏感,增大过盈接触面的摩擦因数,可以改变轴向的接触状态,从而减小轴孔过盈面的微动磨损。
| [1] |
饶振纲. 行星齿轮传动设计[M]. 北京: 化学工业出版社, 2003. RAO Z G. Planetary gear drive design[M]. Beijing: Chemical Industry Press, 2003. |
| [2] |
付彦宏. 190系列柴油机曲轴微动磨损的修复和预防[J]. 石油机械, 1992, 20(10): 34-35. FU Y H. Repair and prevention of fretting wear on crankshaft of 190 series diesel engine[J]. China Petroleum Machinery, 1992, 20(10): 34-35. |
| [3] |
ARCHARD J F. Wear theory and mechanisms:wear control handbook[M]. New York: ASME, 1980: 58.
|
| [4] |
MINDLIN R D. Compliance of elastic bodies in contact:transactions of american society of mechanical engineers[J]. Journal of Applied Mechanics, 1949(16): 259-268. |
| [5] |
周仲荣, LEO VINCENT. 微动磨损[M]. 北京: 科学出版社, 2002. ZHOU Z R, VINCENT L. Fretting wear[M]. Beijing: Science Press, 2002. |
| [6] |
ZHOU Z R, VINCENT L. Mixed fretting regime[J]. Wear, 1995, 181: 531-536. |
| [7] |
ZHOU Z R, CARDOU A, GOUDREAU S, et al. Fretting patterns in a conductor-clamp contact zone[J]. Fatigue & Fracture of Engineering Materials & Structures, 2010, 17(6): 661-669. |
| [8] |
张远彬, 鲁连涛, 宫昱滨, 等. 微动磨损对过盈配合结构微动疲劳性能的影响[J]. 摩擦学学报, 2016, 36(4): 495-505. ZHANG Y B, LU L T, GONG Y B, et al. Influence of fretting wear on fretting fatigue properties of press-fitted shaft[J]. Tribology, 2016, 36(4): 495-505. |
| [9] |
李玲, 麻诗韵, 阮晓光, 等. 加载相位差对微动磨损影响的数值模拟研究[J]. 表面技术, 2018, 47(9): 96-100. LI L, MA S Y, RUAN X G, et al. Numerical simulation of the effect of loading phase difference on fretting wear[J]. Surface Technology, 2018, 47(9): 96-100. |
| [10] |
张远彬, 鲁连涛, 曾东方, 等. 微动磨损对过盈配合结构微动参量的影响[J]. 摩擦学学报, 2015, 35(4): 485-494. ZHANG Y B, LU L T, ZENG D F, et al. Influence of fretting wear on fretting parameters in press-fitted shaft[J]. Tribology, 2015, 35(4): 485-494. |
| [11] |
蔡强, 张翼, 李闯, 等. ZL702A铝合金构件微动疲劳寿命预测研究[J]. 表面技术, 2017, 46(4): 252-257. CAI Q, ZHANG Y, LI C, et al. Fretting fatigue life prediction of ZL702A aluminum alloy components[J]. Surface Technology, 2017, 46(4): 252-257. |
| [12] |
MCVEIGH P A, FARRIS T N. Finite element analysis of fretting stresses[J]. ASME J.Tribology, 1997, 119: 797-801. |
| [13] |
宫昱滨, 鲁连涛, 张远彬. 空心轴过盈配合结构循环微动磨损的仿真研究[J]. 机械工程学报, 2017, 53(6): 123-130. GONG Y B, LU L T, ZHANG Y B, et al. Simulation research on the fretting wear of press-fitted hollow axle[J]. Journal of Mechanical Engineering, 2017, 53(6): 123-130. |
| [14] |
李玲, 康乐, 阮晓光, 等. 不同加载条件下柱面/平面微动磨损有限元分析[J]. 机械科学与技术, 2018, 37(12): 1855-1861. LI L, KANG L, RUAN X G, et al. Finite element analysis of cylinder-flat fretting wear under different loading conditions[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(12): 1855-1861. |
| [15] |
张慧杰, 王志敏, 张太华. 微动工况下柱面不同因素对平面磨损显著性的分析[J]. 工具技术, 2019, 53(1): 47-50. ZHANG H J, WANG Z M, ZHANG T H. Analysis of significance of different factors on flat wear under mirco-motion conditions[J]. Tool Engineering, 2019, 53(1): 47-50. |
| [16] |
霍永忠, 尹东, 赵杰江, 等. 微动磨损与微动疲劳寿命的计算与分析方法[J]. 力学季刊, 2015, 36(2): 165-178. HUO Y Z, YIN D, ZHAO J J, et al. Calculation and analysis method of fretting wear and fretting fatigue life[J]. Chinese Quarterly of Mechanics, 2015, 36(2): 165-178. |
| [17] |
桂长林. Archard的磨损设计计算模型及其应用方法[J]. 润滑与密封, 1990(1): 12-21. GUI C L. The archard design calculation model and its application methods[J]. Lubrication Engineering, 1990(1): 12-21. |



