2. 油气钻井技术国家工程实验室;
3. 中国石油集团工程技术研究院有限公司
2. Oil and Gas Drilling Technology National Engineering Laboratory;
3. CNPC Engineering Technology R & D Company Limited
0 引言
四单根超深井钻机采用四单根立柱进行钻井作业,能够缩短起下钻时间和钻井周期,降低复杂事故发生的概率,满足塔里木油田山前地区深井和超深井提高钻井作业速度及效率的需求[1-2]。四单根立柱较常规的三单根立柱高度增加了9.5 m,立柱排放的稳定性显著降低[3-6]。颜岁娜和徐小鹏等[7-8]通过比较欧拉公式计算得到的失稳临界压应力与有限元计算得到的轴向压应力来判断立柱排放的稳定性。在国外的相关研究中,S.J.SAWARYN等[9-10]采用欧拉公式,计算了立柱在自重作用下的临界屈曲长度,以此判断立柱在靠放工况下的稳定性。以上研究都是以经典欧拉解作为立柱稳定性判定的依据,而经典欧拉公式建立在线弹性条件下[11],实际上部分四单根立柱因发生大的弯曲变形而导致排放困难,立柱大变形问题是典型的几何非线性行为。
为保证立柱排放的稳定性,笔者从非线性的角度出发,采用有限元非线性屈曲计算方法,对不同规格尺寸的四单根立柱排放稳定性进行计算分析,进而给出了四单根钻机立柱的排放方案。
1 立柱排放稳定性分析方法立柱排放稳定性分析主要考虑两种工况[12]:①靠放工况。立柱靠放在井架二层台,其下端支撑在钻台面排放区,上端靠在二层台的指梁上;②移运工况。立柱卸扣后从井口移运到立柱排放区(或是接扣时从立柱排放区移运到井口),此过程的极限状态为,立柱下端位于排放区最远端,而上端由顶驱吊卡夹持,位于井口中心线上。
石油钻井立柱属于典型的细长杆结构,上述2种工况中,立柱上下两端的约束可视为铰支约束。因此,立柱排放的稳定性分析即为判别两端铰支的细长杆在自重作用下是否失稳屈曲。当立柱在自重作用下发生失稳屈曲时,前一种工况下立柱产生大变形而不能稳定地靠放在二层台指梁上,后一种工况下立柱最大弯曲度超过顶驱背梁,井架工无法摘扣吊卡。
屈曲分析包括经典欧拉公式法和有限元法[11]。根据欧拉公式,两端铰支立柱屈曲的最小极限载荷PCR的计算式为:
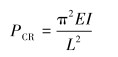
|
(1) |
其中:
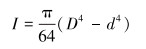
|
(2) |
式中:E为弹性模量,I为惯性矩,L为管体长度,D为钻柱外径,d为钻柱内径。
从式(1)可以看出,立柱高度从28.0 m增加到37.5 m,长度增加了34%,而极限载荷则降低到原来的56%,几乎为原来的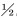
在有限元分析中,屈曲分析包含两种方法:特征值屈曲分析和非线性屈曲分析。前一种分析结果为非保守结果,与经典欧拉解相当,通常不能用于工程分析;后一种分析较前一种精确[13]。因此,笔者主要采用后一种方法,即非线性屈曲法,分析并判定立柱排放的稳定性。立柱非线性屈曲有限元计算模型如图 1所示。立柱采用Beam188梁单元进行有限元模拟,共产生56个节点,55个单元。下端约束处节点释放X向和Z向旋转自由度,上端约束处节点约束X向和Z向平移自由度。将重力作为惯性力处理,施加的载荷为重力加速度。

|
| 图 1 立柱非线性屈曲有限元计算模型 Fig.1 Finite element model of stand nonlinear buckling |
2 立柱排放稳定性非线性屈曲分析
立柱排放稳定性非线性屈曲分析涉及2种工况:立柱靠放工况和立柱移运工况。表 1列出了常用钻柱规格。
| 类型 | 规格/in | 外径/mm | 壁厚/mm |
3  |
88.9 | 9.35 | |
| 4 | 101.6 | 8.38 | |
| 钻杆 | 4 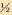 |
114.3 | 8.56 |
| 5 | 127.0 | 9.19 | |
5 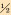 |
139.7 | 9.17 | |
3 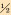 |
88.9 | 11.40 | |
| 4 | 101.6 | 9.56 | |
| 加重钻杆 | 4 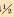 |
114.3 | 10.92 |
| 5 | 127.0 | 12.70 | |
5 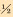 |
139.7 | 10.54 | |
4 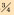 |
120.7 | 34.95 | |
| 钻铤 | 5 | 127.0 | 34.90 |
6 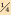 |
158.8 | 50.80 | |
| 7 | 177.8 | 60.30 |
2.1 四单根立柱靠放稳定性分析
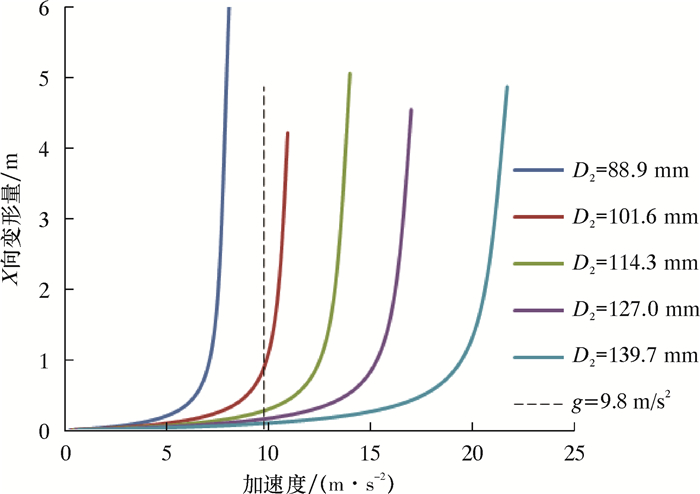
通过有限元非线性屈曲分析,得到立柱靠放工况下不同规格的钻杆、加重钻杆和钻铤变形随加速度载荷变化曲线,如图 2、图 3和图 4所示。图中D1、D2和D3分别表示钻杆外径、加重钻杆外径和钻铤外径,X向变形量为总变形量的主要分量。由于考虑的是立柱在自重作用下的变形行为,有限元模型中施加的重力加速度为特定的加速度载荷,取值9.8 m/s2。为了求得立柱的屈曲载荷,载荷的施加做了技巧性处理,立柱上施加了较重力加速度载荷高出一定量的加速度载荷,这一加速度载荷近似为1阶特征值屈曲载荷,即为通过特征值屈曲计算得到的非保守结果。如图 2所示,以ø139.7 mm钻杆为例,所施加的加速度载荷最大值为22 m/s2,并设置若干计算子步,这样得到立柱上变形最大处节点的X向变形量随加速度载荷的变化曲线图。从图 2可以看出,随着加速度的增大,立柱从开始变形到屈曲,经历缓慢变形①、加速变形②和迅速变形失稳③三个阶段。当在横坐标上取加速度载荷为9.8 m/s2时,即为重力加速度,只需查看重力加速度值处于哪个阶段,即可判别立柱的稳定性。从立柱排放安全的角度出发,认为当重力加速度处于缓慢变形阶段①时,立柱的排放稳定安全。

|
| 图 2 靠放工况下不同规格钻杆受力变形曲线 Fig.2 Deformation curve of the drill pipe with different specifications under lean condition |
|
| 图 3 靠放工况下不同规格加重钻杆受力变形曲线 Fig.3 Deformation curve of the heavy weight drill pipe with different specifications under lean condition |
|
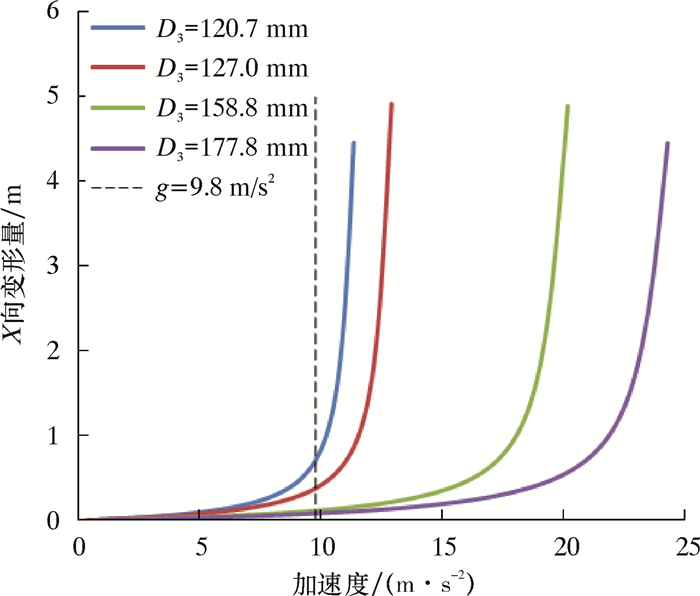
| 图 4 靠放工况下不同规格钻铤受力变形曲线 Fig.4 Deformation curve of the drill collar with different specifications under lean condition |
由计算结果可以看出:对同一类型的立柱,随着外径的增大,其变形量逐步减小,而稳定性越来越好;根据立柱稳定性判定方法,靠放工况下四单根立柱适用钻柱尺寸为ø114.3 mm及以上直径钻杆和加重钻杆,ø127.0 mm及以上直径钻铤。
2.2 四单根立柱移运稳定性分析四单根立柱的稳定性要求同时满足靠放和移运两种工况。通过计算,得到立柱移运工况下不同规格的钻杆、加重钻杆和钻铤的变形随加速度载荷的变化曲线,如图 5、图 6和图 7所示。对于靠放工况下稳定性不够的钻杆或是钻铤,无需再做移运工况下的计算。
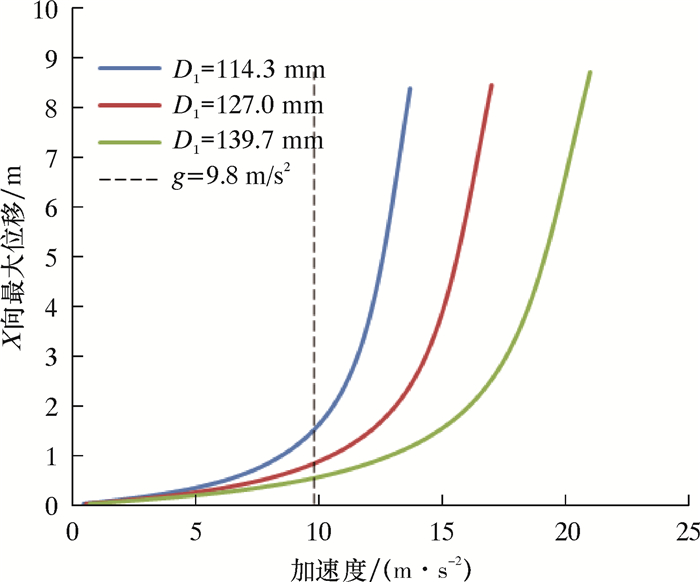
|
| 图 5 移运工况下不同规格钻杆受力变形曲线 Fig.5 Deformation curve of the drill pipe with different specifications under moving condition |
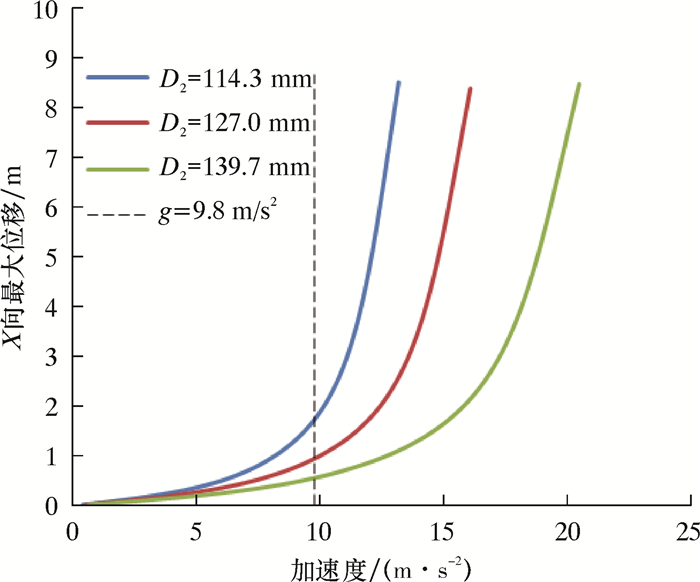
|
| 图 6 移运工况下不同规格加重钻杆受力变形曲线 Fig.6 Deformation curve of the heavy weight drill pipe with different specifications under moving condition |
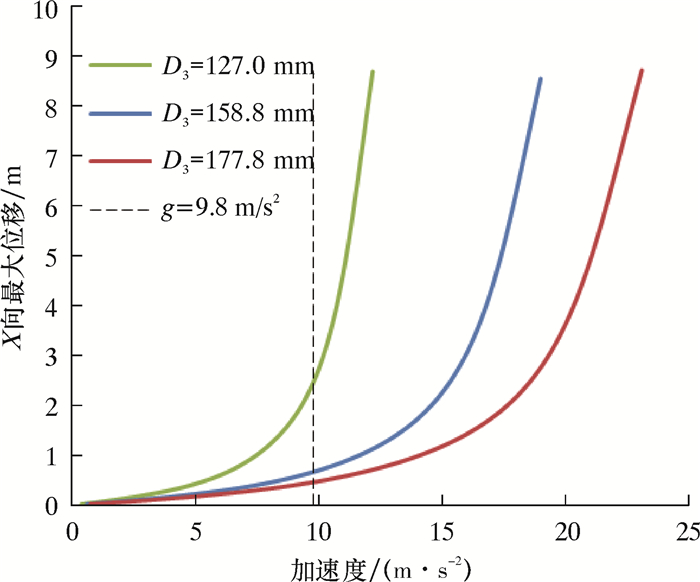
|
| 图 7 移运工况下不同规格钻铤受力变形曲线 Fig.7 Deformation curve of the drill collar with different specifications under moving condition |
根据立柱稳定性判定方法,综合靠放工况和移运工况下的计算结果可以得出结论:ø127.00 mm及以上直径钻杆和加重钻杆、ø158.8 mm及以上直径钻铤能满足四单根立柱排放稳定性要求。
2.3 三单根立柱排放稳定性分析对于不满足四单根立柱稳定性要求的钻杆或钻铤,可选择使用三单根立柱,这就要求井架上增加三单根二层台。
加重钻杆相比较于常规钻杆壁厚大、内径小,由式(1)可知其极限屈曲载荷较常规钻杆小。通过图 2与图 5(或图 3与图 6、图 4与图 7)比较靠放工况和移运工况立柱的稳定性,发现移运工况下立柱的稳定性更差。因此,对于三单根立柱的稳定性而言,仅通过计算验证三单根立柱(加重钻杆和钻铤)移运状况下的稳定性,计算结果如图 8所示。由图 8可知,对于三单根立柱而言,ø88.9、ø101.6和ø114.3 mm加重钻杆以及ø120.7和ø127.0 mm钻铤,其排放稳定性满足要求,这与常规三单根钻机的情况相符。
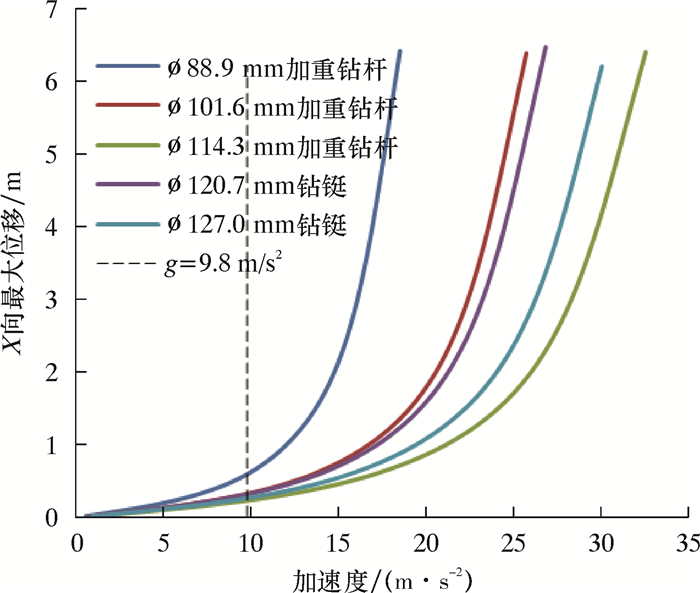
|
| 图 8 移运工况下不同规格加重钻杆和钻铤受力变形曲线 Fig.8 Deformation curve of the heavy weight drill pipe and drill collar with different specifications under moving condition |
综合以上分析结果,给出立柱排放方案:ø127.0 mm及以上直径钻杆和加重钻杆、ø158.8 mm及以上直径钻铤采用四单根立柱;ø158.8 mm以下钻杆和加重钻杆、ø158.8 mm以下钻铤采用三单根立柱,如表 2所示。表 2中的“三”表示三单根立柱,“四”表示四单根立柱。
| 外径/mm | 88.9 | 101.6 | 114.3 | 127.0 | 139.7 | 120.7 | 127.0 | 158.8 | 177.8 |
| 钻杆 | 三 | 三 | 三 | 四 | 四 | — | — | — | — |
| 加重钻杆 | 三 | 三 | 三 | 四 | 四 | — | — | — | — |
| 钻铤 | — | — | — | — | — | 三 | 三 | 四 | 四 |
3 现场试验
四单根超深井钻机在投入现场试验后,结合计算分析给出的立柱排放方案,开展了立柱的稳定性测试。试验钻机新增加了三单根二层台,如图 9所示。现场试验结论与有限元分析给出的方案一致。图 10、图 11和图 12分别为收集到的现场四单根立柱(钻杆和钻铤)在排放过程中的形态。

|
| 图 9 试验钻机四单根二层台和三单根二层台 Fig.9 Test rig monkey board for the four quadruple-joint stand and the triple-joint stand |
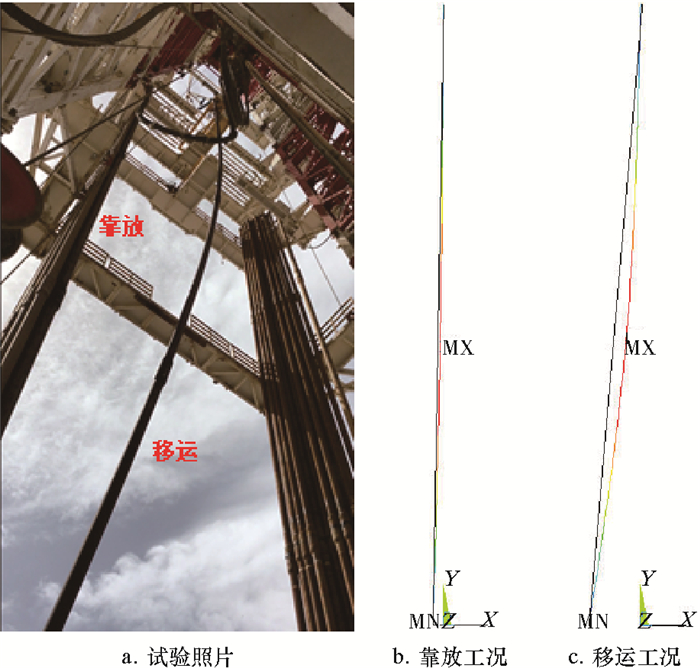
|
| 图 10 ø127.0 mm钻杆排放情况 Fig.10 ø127.0 mm drill pipe handling |
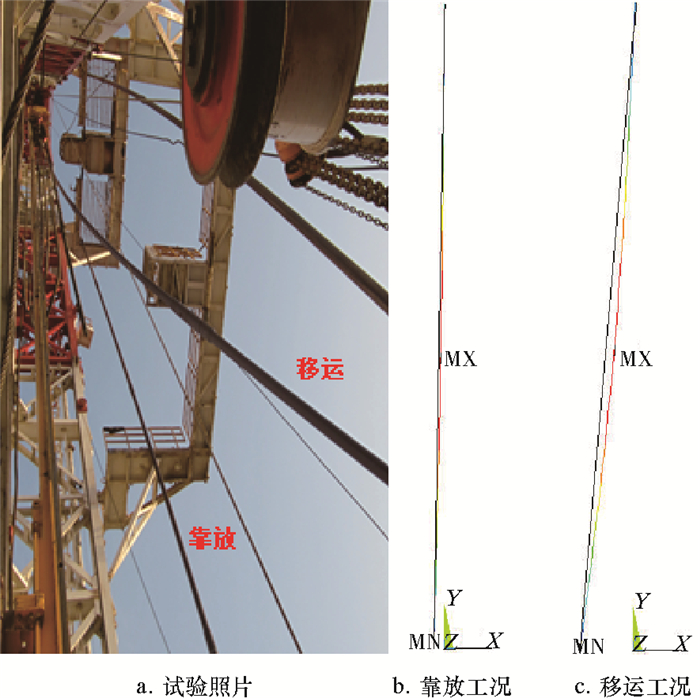
|
| 图 11 ø139.7 mm钻杆排放情况 Fig.11 ø139.7 mm drill pipe handling |

|
| 图 12 ø158.8 mm钻铤排放情况 Fig.12 ø158.8 mm drill collar handling |
笔者将有限元计算得到的立柱在自重下的变形形态与现场排放过程中立柱的变形形态进行对比,结果发现计算得到的立柱在自重下的变形形态与现场试验相符。在立柱靠放工况下,ø127.0 mm钻杆的最大变形量为141 mm,ø139.7 mm钻杆的最大变形量为96 mm,ø158.8 mm钻铤的最大变形量为118 mm;在立柱移运工况下,ø127.0 mm钻杆的最大变形量为837 mm,ø139.7 mm钻杆的最大变形量为544 mm,ø158.8 mm钻铤的最大变形量为672 mm。
4 结论(1) 同一类型的立柱,随着钻具直径的增大,其变形量逐步变小,稳定性越来越好。
(2) ø127.0 mm及以上规格钻杆和加重钻杆、ø158.8 mm及以上规格钻铤,采用四单根立柱;ø127.0 mm以下常用钻杆和加重钻杆、ø158.8 mm以下常用钻铤,采用三单根立柱,钻机增加三单根二层台。
(3) 立柱稳定性非线性屈曲分析结果与现场变形情形相符,不同规格的钻柱排放方案得到现场试验验证。
| [1] |
左卫东, 方太安, 周志雄, 等. 四单根立柱超深井钻机井架液压辅助起升机理[J]. 石油机械, 2018, 46(8): 1-5. ZUO W D, FANG T A, ZHOU Z X, et al. Mechanism of hydraulic assisted lifting for quadruple-joins stand ultra-deep drilling rig derrick[J]. China Petroleum Machinery, 2018, 46(8): 1-5. |
| [2] |
张益, 陈思祥, 张友会, 等. ZJ90/6750DB-S四单根立柱高效钻机关键技术研究[J]. 机械工程师, 2017(7): 117-119. ZHANG Y, CHEN S X, ZHANG Y H, et al. Development of ZJ90/6750DB-S four single column in ultra deep drilling rig[J]. Mechanical Engineer, 2017(7): 117-119. DOI:10.3969/j.issn.1002-2333.2017.07.051 |
| [3] |
白海永, 方永利. ANSYS极限载荷分析法在压力容器设计中的应用[J]. 压力容器, 2014, 31(6): 47-50. BAI H Y, FANG Y L. Application of ANSYS limit load analysis method in pressure vessel design stand[J]. Pressure Vessel Technology, 2014, 31(6): 47-50. DOI:10.3969/j.issn.1001-4837.2014.06.007 |
| [4] |
署恒木. 自重作用下长管柱稳定性分析[J]. 青岛大学学报, 2000, 15(2): 63-66. SHU H M. Analysis of buckling for long pipe string under gravity[J]. Journal of Qingdao University, 2000, 15(2): 63-66. DOI:10.3969/j.issn.1006-9798.2000.02.018 |
| [5] |
崔孝秉, 张宏, 宋治. 套管柱稳定性问题研究[J]. 石油学报, 1998, 19(1): 114-118. CUI X B, ZHANG H, SONG Z. A research on casing string stability of oil well[J]. Acta Petrolei Sinica, 1998, 19(1): 114-118. DOI:10.3321/j.issn:0253-2697.1998.01.022 |
| [6] |
孟祥龙, 鲜海波, 曾峰, 等. 轴力作用下钻柱稳定性分析[J]. 中国科技论文在线, 2010, 5(11): 868-870. MENG X L, XIAN H B, ZENG F, et al. Stability analysis of drill pipe under axial force[J]. China Sciencepaper, 2010, 5(11): 868-870. DOI:10.3969/j.issn.2095-2783.2010.11.007 |
| [7] |
颜岁娜, 张益, 张友会, 等. 4单根立柱钻机钻柱靠放分析[J]. 石油机械, 2016, 44(11): 14-18. YAN S N, ZHANG Y, ZHANG Y H, et al. Racking stability analysis on 4 joints stand[J]. China Petroleum Machinery, 2016, 44(11): 14-18. |
| [8] |
徐小鹏, 王定亚, 邓勇, 等. 四单根立柱钻机关键技术研究与提效分析[J]. 石油机械, 2018, 46(12): 17-23. XU X P, WANG D Y, DENG Y, et al. Key technologies and efficiency improvement analysis of four-joint stand drilling rig[J]. China Petroleum Machinery, 2018, 46(12): 17-23. |
| [9] |
SAWARYN S J. The stability of a pipe stand racked in a derrick part 1: foundation[R]. SPE 163484-MS, 2013.
|
| [10] |
SAWARYN S J, PATTILLO P D. The stability of a pipe stand racked in a derrick part 2: a general pipe-stand model[R]. SPE 163535-MS, 2013.
|
| [11] |
单祖辉. 材料力学Ⅰ[M]. 北京: 高等教育出版社, 2009: 328-334. SHAN Z H. Mechanics of materials I[M]. Beijing: Higher Education Press, 2009: 328-334. |
| [12] |
蔡文军, 张慧峰, 孙长征, 等. 钻柱自动化排放技术发展现状[J]. 石油机械, 2008, 36(12): 71-74. CAI W J, ZHANG H F, SUN C Z, et al. Development status of drill string automation handling technology[J]. China Petroleum Machinery, 2008, 36(12): 71-74. |
| [13] |
CAD/CAM/CAE技术联盟. ANSYS 15.0有限元分析从入门到精通[M]. 北京: 清华大学出版社, 2016: 295-309.
|
| [24] |
CAD/CAM/CAE Technology Alliance. ANSYS 15.0 finite element analysis from entry to the master[M]. Beijing: Tsinghua University Press, 2016: 295-309.
|


