2. 长江大学机械工程学院
2. School of Mechanical Engineering, Yangtze University
0 引言
近年来,连续管作业技术已经愈发成熟。截止到2018年,全球范围内应用的连续管作业机共有1 955台[1]。但是,连续管仍然存在使用寿命较短等缺点[2]。影响连续管使用寿命的因素有很多,其中疲劳寿命是关键的限制因素[3]。由于连续管在作业过程中需要承受重载、腐蚀等工况[4],必然要对连续管材料提出更高的力学性能要求,而CT110材料具有抗疲劳、抗拉强度高、耐腐蚀及耐氧化等综合优良性能,所以常被选用为制造连续管的材料[5]。
合金材料的疲劳寿命与材料成分[6]、晶粒尺寸[7]、应力比[8]、平均应力[9]以及加载频率[10]等变量密切相关,其中应力比对合金材料的疲劳寿命影响最大,因此,本文研究了不同应力比下的含裂纹缺陷连续管裂纹扩展速率。在循环载荷作用下,合金材料疲劳寿命Nf=疲劳裂纹萌生寿命Ni+裂纹扩展寿命Np。相关研究结果表明[11], 对于已存在裂纹的构件,Np几乎等于Nf。此时,要建立精确的疲劳裂纹扩展速率的表达式,就可通过积分计算疲劳寿命,从而预测构件的剩余疲劳寿命,做到及时维护或更换,防止因连续管疲劳断裂失效而引发严重的作业事故。
目前合金材料的疲劳裂纹扩展研究主要通过试验法,但是在研究不同应力比的CT110材料疲劳扩展速率规律时,所需数据较多,较为繁琐。而扩展有限元法(XFEM)在模拟材料疲劳裂纹扩展时具有计算结果相对精确以及操作过程简单等优点。因此,本文基于扩展有限元法得到CT110合金疲劳裂纹扩展速率,并采用Paris公式,分别对不同应力比条件下的疲劳裂纹扩展速率进行预测。
1 XFEM理论方法XFEM相对于常规有限元法的主要优势就是它允许裂纹在单元内部或穿过单元,在模拟裂纹扩展时不需要重新划分网格,也无需考虑裂纹的内部细节。在模拟连续管的裂纹扩展时,常常利用水平集法追踪非连续间断面。
XFEM允许不连续面[11](如裂纹、间断等)穿过单元,即网格需要独立于间断面,因此常常需要借助水平集法对不连续面进行几何描述。此外,在XFEM中,构造扩充形函数也需要借助水平集函数。
水平集法[12-14]可以准确地定位间断面,它可以将裂纹面S的位置用水平集函数通用符号距离函数进行描述,具体的符号距离函数的表达式为:
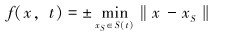
|
(1) |
式中:S为间断面所有离散节点的集合;x为计算域内任意一节点;t为计算域内任意一时间点;xS为间断面任意一节点。
公式(1)的物理意义为计算域内任意一点的符号距离函数等于从这一点到间断的最短距离,并且在间断两边的点具有不同的符号。对于有端点的间断,仅有距离符号函数还不够,它无法反映出裂纹尖端的位置。因此,需要对每一个端点分别定义一个水平集函数gi。

|
(2) |
式中:xi为端点,vi为端点移动速度,m/s。
由式(2)可以看出,gi=0代表了经过端点xi并与裂纹扩展速度vi垂直的一条直线,即该直线相交于裂纹尖端并垂直于裂纹扩展方向,其几何描述如图 1所示。

|
| 图 1 水平集函数f和g表示的裂纹S Fig.1 Crack S expressed by Level set function f and g |
2 基于XFEM的疲劳裂纹扩展模型验证
为验证用XFEM模拟合金材料裂纹扩展的可靠性,参照李其棒[15]的研究数据,建立了相关有限元模型,该模型的尺寸及样式如图 2所示。笔者将通过试验法测得的试件循环次数与通过XFEM模拟测得的试件循环次数进行对比,以分析误差大小。

|
| 图 2 模拟试样尺寸 Fig.2 Dimension of the simulated sample |
2.1 有限元模型建立 2.1.1 网格划分
网格划分方式如图 3所示。局部放大部分的中间线为预置裂纹,预置裂纹长度为2 mm,根据试验法已知的裂纹扩展路径,可以预测XFEM裂纹扩展的模拟路径将处于模型的上、下对称面区域,因此,将该区域进行加密。为了避免网格布置对裂纹扩展路径的影响,将模型的上下相关边界对称布置,使网格完全对称。

|
| 图 3 有限元模型网格划分方式 Fig.3 Finite element model meshing |
2.1.2 分析步和加载设置
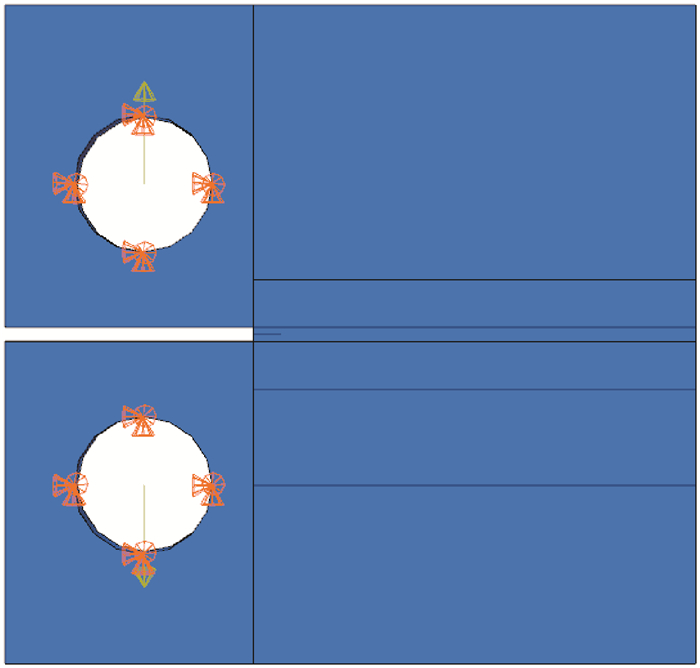
在ABAQUS中建立一个最小增量步为1,最大增量步为200,最大总步数为100万的疲劳循环分析步。场输出变量包括节点扩展有限元水平集函数PHILSM、PSILSM、单元裂纹起裂循环次数、单元应变、扩展有限元单元状态(STATUSXFEM)以及单元应力等。加载及边界条件如图 4所示。在试件的上下两孔设置边界条件,使得两孔的X、Y方向位移为0。将两孔的表面耦合在rp1和rp2两参考点上,在两参考点上分别施加集中力load1和load2。
|
| 图 4 有限元模型加载及边界条件 Fig.4 Finite element model loading and boundary conditions |
由于为周期载荷,需定义幅值函数AMP,其函数如式(3)所示。

|
(3) |
式中:A0为初始幅值,N;A1为余弦幅值系数;B1为正弦幅值系数;ω为频率,Hz;t为循环时间,s;t0为初始循环时间,s。
2.2 有限元模型验证选取文献[15]中试样1、试样2、试样3和试样4四个试样的试验数据,其试样的尺寸及加载如表 1所示。将试验法测得的数据与XFEM模拟得到的数据(记录裂纹扩展到15 mm的数据)进行对比,其结果如表 2所示。
| 试样编号 | 应力比 | 最大拉载/kN | 壁厚/mm |
| 1 | 0.02 | 8.5 | 6.4 |
| 2 | 0.02 | 8.8 | 6.8 |
| 3 | 0.02 | 7.0 | 6.8 |
| 4 | 0.02 | 7.5 | 6.8 |
| 试样编号 | 试验循环次数 | 模拟循环次数 | 误差/% |
| 1 | 50 080 | 58 930 | 17.67 |
| 2 | 70 806 | 81 380 | 14.93 |
| 3 | 135 375 | 150 250 | 10.99 |
| 4 | 179 672 | 195 100 | 8.59 |
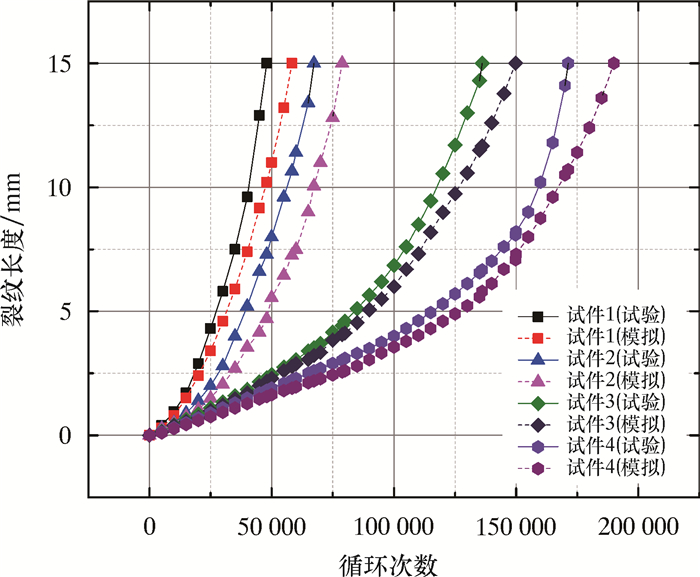
试验法和模拟法测得的合金材料裂纹长度a与循环次数N的关系如图 5所示。
|
| 图 5 GH4133B合金疲劳裂纹扩展循环次数比较 Fig.5 Comparison of fatigue crack propagation cycles of the GH4133B alloy |
从表 2可以看出,通过试验法测得的试件循环次数与通过XFEM模拟测得的试件循环次数的最大误差为17.67%,处于工程允许的20%误差范围内,并且随着(试验)循环次数的增加,误差也在不断减小。由此可知,XFEM模拟合金材料的裂纹扩展是相对精确的。
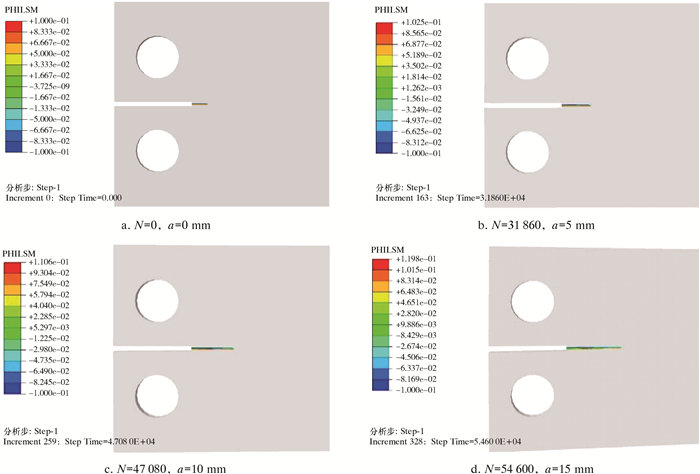
试件1的疲劳裂纹扩展模拟过程如图 6所示。图 6中:PHILSM为水平集量,作用是追踪裂纹扩展路径;a为扩展后裂纹长度(图 6a的裂纹为预置裂纹,长度为2 mm)。
|
| 图 6 试件1疲劳裂纹扩展模拟过程 Fig.6 Fatigue crack propagation simulation process of specimen 1 |
用割线法对图 5中数据进行处理。割线法是用相邻的两个数据点连线的直线斜率来表示增量(ai+1-ai)的平均速率,直线斜率通常表示如下:

|
(4) |
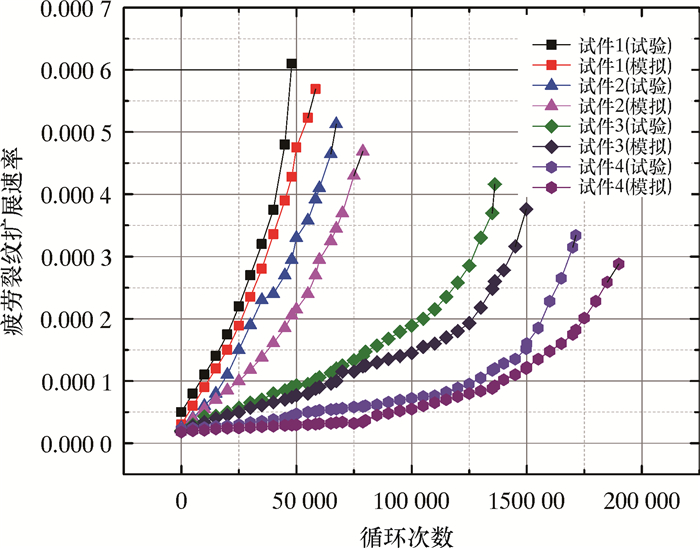
根据式(4)得到的疲劳循环速率与循环次数的关系如图 7所示。
|
| 图 7 GH4133B合金疲劳裂纹扩展速率的比较 Fig.7 Comparison of fatigue crack propagation rate of the GH4133B alloy |
从图 6和图 7可以看出,用XFEM模拟与试验法得到的GH4133B合金材料裂纹扩展规律基本一致,都随着循环步数的增加其裂纹扩展速度不断加快,这也进一步证明了用XFEM模拟合金材料裂纹扩展的可靠性。
3 CT110钢疲劳裂纹扩展模拟连续管疲劳为大应力低周疲劳,连续管的疲劳寿命几乎等于连续管的裂纹扩展寿命。当含裂纹缺陷连续管的应力强度因子ΔK≤ΔKth(应力强度因子门槛值)时,连续管处于裂纹萌生阶段;当含裂纹缺陷连续管的应力强度因子ΔK>ΔKth时,连续管进入裂纹扩展阶段。随着裂纹不断扩展,其应力强度因子在不断增大,即此时连续管材料处于高应力状态,裂纹扩展速率不断增大达到较大值,前述研究方法适用于连续管低周疲劳。因此,计算连续管的应力强度因子门槛值ΔKth非常关键。
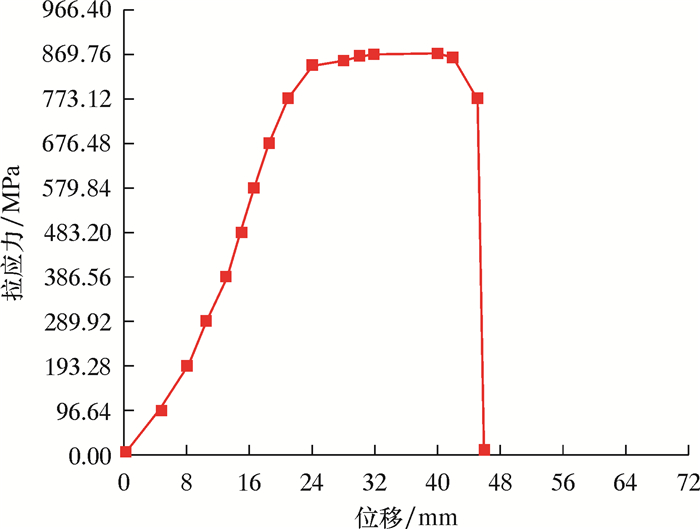
由连续管工程技术手册[16]可知,CT110钢的屈服强度为871 MPa,抗拉强度为910 MPa,伸长率为21%,弹性模量为231 GPa,泊松比为0.303。根据拉伸试验测得CT110钢的拉应力-位移曲线,如图 8所示。
|
| 图 8 CT110钢拉应力-位移曲线 Fig.8 The tensile stress-displacement curve of the CT110 steel |
将图 8的拉应力-位移曲线进行积分,得到CT110合金钢在常温下的断裂能约为2.83×107 J/m3。由于ABAQUS的计算模型是利用基于能量线性软化和幂法则混合模型计算损伤演化,所以将断裂能设为2.83×107 J/m3,平面内、外的剪切断裂能也设为2.83×107 J/m3,幂法则的指数设为1.0。
为研究应力比R对CT110材料裂纹扩展门槛值的影响,分别设置了R=0.02、0.10、0.20、0.30、0.40和0.50共6组试样,具体参数设置如表 3所示。
| 试样编号 | 应力比 | 最大拉载/kN | 壁厚/mm |
| 1 | 0.02 | 6 | 6 |
| 2 | 0.10 | 6 | 6 |
| 3 | 0.20 | 6 | 6 |
| 4 | 0.30 | 6 | 6 |
| 5 | 0.40 | 6 | 6 |
| 6 | 0.50 | 6 | 6 |
根据标准CT试件对于每一步裂纹扩展中的应力强度因子计算公式[17],则有:

|
(5) |

|
(6) |
式中:ΔF为载荷幅(ΔF=Fmax-Fmin),N;W为试样宽度,m;B为试样厚度,m;α =l/W,l为有效裂纹长度,m。
根据图 1所示的CT标准试件,此处,l=0.01 m,W=0.04 m,B=0.006 m。
对于疲劳裂纹扩展门槛值的测定,采用逐级降载法加载,初始疲劳载荷峰值Pmax=6 kN,每级降载为5%(保持应力比R不变),每级载荷下的裂纹增量Δa=0.25 mm。
4 模拟结果及分析 4.1 疲劳裂纹扩展速率对于常幅疲劳,不同应力比下的疲劳裂纹扩展速率曲线分为稳定扩展阶段(Paris)和快速扩展阶段。采用Paris公式进行疲劳裂纹扩展的数据进行回归分析。Paris公式为:

|
(7) |
对式(7)两边分别取对数,则有:
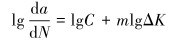
|
(8) |
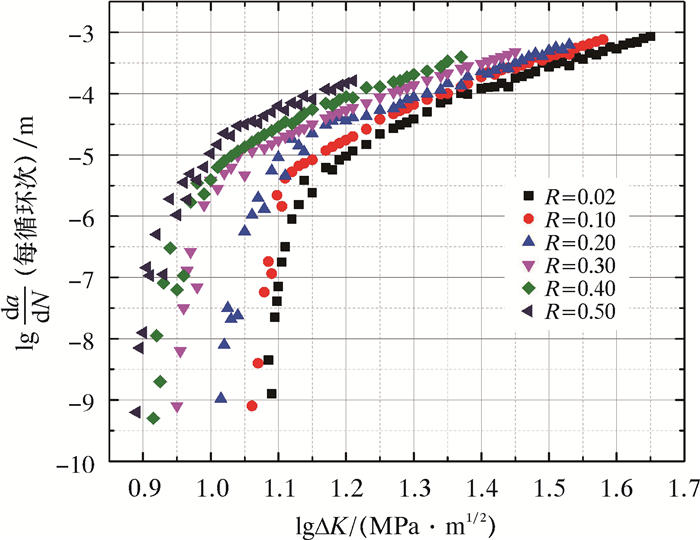
由式(8)可以看出,稳定扩展阶段的疲劳裂纹扩展速率da/dN与应力强度因子幅值ΔK在对数坐标下为线性关系,将相关数据进行处理后,得到的6组试样的


|
| 图 9 不同应力比疲劳裂纹扩展速率曲线 Fig.9 Effect of stress ratio on the fatigue crack propagation rate |

|
| 图 10 稳定扩展阶段(Paris区)裂纹扩展速率拟合曲线 Fig.10 Fatigue crack propagation rate fitting curve in the stable propagation phase (Paris zone) |
| R | m | lgC | 拟合公式 | 拟合度 |
| 0.02 | 3.457 4 | -8.769 52 | 
|
0.979 90 |
| 0.10 | 3.597 3 | -8.796 49 | 
|
0.983 63 |
| 0.20 | 3.759 2 | -8.909 31 | 
|
0.987 57 |
| 0.30 | 3.883 3 | -8.932 29 | 
|
0.983 33 |
| 0.40 | 4.061 4 | -8.965 84 | 
|
0.987 76 |
| 0.50 | 4.551 1 | -9.280 66 | 
|
0.974 25 |
由表 4可以看出,随着应力比R的增大,CT110钢的材料常数m不断增大,即CT110钢疲劳裂纹扩展的加速度不断增大。
表 5为ΔK一定时疲劳裂纹扩展速率。
| ΔK/(MPa·m1/2) | 疲劳裂纹扩展速率 (每循环次)/10-4 m
(每循环次)/10-4 m |
||||
| R=0.02 | R=0.10 | R=0.20 | R=0.30 | R=0.40 | |
| 20 | 1.000 | 1.549 | 2.040 | ||
| 30 | 2.089 | 3.162 | 4.467 | ||
由表 5可知:当应力强度因子幅值ΔK一定时,疲劳裂纹扩展速率随着应力比R的增大而增大,当应力强度因子幅值ΔK=20 MPa·m1/2、应力比由0.2增长到0.4时,疲劳裂纹扩展速率由每循环次10-4m增长到每循环次2.04×10-4m,增幅为104%;当ΔK=30 MPa·m1/2、应力比由0.02增长到0.20时,疲劳裂纹扩展速率由每循环次2.089×10-4 m增长到每循环次4.467×10-4 m,增幅为113.8%。
4.2 疲劳裂纹扩展门槛值在对CT110钢的疲劳裂纹扩展模拟过程中,采用逐级降载的方式获取其疲劳裂纹扩展门槛值。原理是当载荷降到一定程度时,CT110钢的疲劳裂纹扩展速率会出现断崖式下降,此时,裂纹几乎不再扩展。取断崖式下降段的数据点(至少5组数据)进行线性回归拟合,拟合的直线与da/dN=10-7 m/循环次交点对应的应力强度因子范围ΔK,即为CT110钢裂纹扩展门槛值ΔKth。其结果如表 6所示。从表 6可知,CT110钢的裂纹扩展门槛值随着应力比R的增大而减小,当应力比由0.02增大到0.50时,其疲劳裂纹门槛值下降了37%。
| R | 0.02 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
| ΔKth/(MPa·m1/2) | 12.78 | 12.02 | 10.71 | 9.24 | 8.55 | 8.07 |
5 结论
(1) 利用ABAQUS软件平台的扩展有限元法功能,可以较为精确地模拟连续管用CT110疲劳裂纹扩展过程。
(2) 采用Paris公式对
(3) 采用逐级降载法获得了不同应力比下CT110钢的裂纹扩展门槛值,随着应力比的增大,其疲劳裂纹扩展门槛值不断减小。当应力比由0.02增大到0.50时,其疲劳裂纹门槛值下降了37%,表明应力比对裂纹扩展门槛值的影响较大。
| [1] |
Intervention & Coiled Tubing Association. Worldwide coiled tubing rig count[EB/OL]. (2017-12)[2018-08-01]. http://www.icota.com/ctrigcount.htm.
|
| [2] |
李子丰, 李雪娇, 王鹏. 预弯曲连续油管及其疲劳寿命预测[J]. 石油学报, 2012, 33(4): 706-710. LI Z F, LI X J, WANG P. Pre-bending coiled tubing and its fatigue life prediction[J]. Acta Petrolei Sinica, 2012, 33(4): 706-710. |
| [3] |
LIU S H, XIAO H, GUAN F, et al. Coiled tubing failure analysis and ultimate bearing capacity under multi-group load[J]. Engineering Failure Analysis, 2017, 79(9): 803-811. |
| [4] |
VAN ADRICHEM W P. Coiled tubing failure statistics used to develop tubing performance indicators[R]. SPE 54478-MS, 1999.
|
| [5] |
毕宗岳, 鲜林云, 汪海涛, 等. 国产超高强度CT110连续管组织与性能[J]. 焊管, 2017, 40(3): 24-27. BI Z Y, XAN L Y, WANG H T, et al. Microstructure and mechanical properties of domestic ultra high strength CT110 grode coiled tubing[J]. Welded Pipe, 2017, 40(3): 24-27. |
| [6] |
TSAI Y L, WANG S F, BOR H Y, et al. Effects of alloy elements on microstructure and creep properties of fine-grained nickel-based superalloys at moderate temperatures[J]. Materials Science and Engineering A, 2013, 571: 155-160. DOI:10.1016/j.msea.2013.02.002 |
| [7] |
JIANG R, EVERITT S, LEWANDOWSKI M, et al. Grain size effects in a Ni-based turbine disc alloy in the time and cycle dependent crack growth regimes[J]. International Journal of Fatigue, 2014, 62: 217-227. DOI:10.1016/j.ijfatigue.2013.07.014 |
| [8] |
ZHENG J, POWELL B E. Effect of stress ratio and test methods on fatigue crack growth rate for nickel based superalloy Udimet720[J]. International Journal of Fatigue, 1999, 21(5): 507-513. DOI:10.1016/S0142-1123(99)00009-2 |
| [9] |
FANG D N, BERKOVITS A. Mean stress models for low-cycle fatigue of a nickel-base superalloy[J]. International Journal of Fatigue, 1994, 16(4): 429-437. |
| [10] |
PRASAD K, BABU N C, KUMAR V. Effect of frequency and orientation on fatigue crack growth behavior of forged turbine disc of IN 718 superalloy[J]. Materials Science and Engineering A, 2012, 544: 414-426. |
| [11] |
余天堂. 不连续问题的扩展有限元法分析[J]. 船舶力学, 2007, 11(5): 716-722. YU T T. Extended finite element medhod analysis of discontinuities[J]. Journal of Ship Mechanics, 2007, 11(5): 716-722. DOI:10.3969/j.issn.1007-7294.2007.05.009 |
| [12] |
庄茁, 柳占立, 成斌斌, 等. 扩展有限单元法[M]. 北京: 清华大学出版社, 2012. ZHUANG Z, LIU Z L, CHENG B B, et al. Extended finite element method[M]. Beijing: Tsinghua University Press, 2012. |
| [13] |
GINER E, SUKUMAR N, TARANCON J E, et al. An Abaqus implementation of the extended finite element method[J]. Engineering Fracture Mechanics, 2008, 76: 347-350. |
| [14] |
GHAFFARI D, AHMADI S R, SHABANI F. XFEM simulation of a quenched cracked glass plate with moving convective boundaries[J]. Comptes Rendus Mecanique, 2016, 344(2): 78-94. DOI:10.1016/j.crme.2015.09.007 |
| [15] |
李其棒.航空发动机涡轮盘用GH4133B合金疲劳裂纹扩展数值模拟研究[D].湖南: 湘潭大学, 2013. LI Q B. Aeroengien turbine disk GH4133B alloy fatigue crack propagation numerical simulation study[D]. Hunan: Xiangtan University, 2013. |
| [16] |
赵章明. 连续油管工程技术手册[M]. 北京: 石油工业出版社, 2003: 74-78. ZHAO Z M. Coiled tubing engineering manual[M]. Beijing: Petroleum Industry Press, 2003: 74-78. |
| [17] |
中国钢铁工业协会, 全国钢标准化技术委员会.金属材料-疲劳试验-疲劳裂纹扩展方法: GB/T 6398-2017[S].北京: 中国标准出版社, 2017. China Iron and Steel Association, National Steel Standardization Technical Committee.Metallic materials-Fatigue testing-Fatigue crack growth method: GB/T6398-2017[S]. Beijing: China Standard Press, 2017. |



