0 引言
在压裂作业过程中,泵头体作为压裂泵的液力端,在高压循环载荷激励下,很容易产生强烈的振动。同时,压裂车泵出的不均匀压裂液对排出管汇产生随时间变化的激振力,使得压裂管汇产生强烈的耦合振动。这种振动是引起压裂管件疲劳破坏的主要原因之一。因此,研究高压管汇的振动规律,提出合理减振措施,对避免共振,减少因振动引起的工程事故具有重要的指导意义。
国内外大量的研究人员对此进行了许多研究,M.P.PAÍDOUSSIS等[1-2]建立了描述输流管道非线性动力学行为的流固耦合振动模型,分析了脉动流体对输流管道振动特性的影响规律;M.H.GHAYESH[3]分析了弹性支撑对管道非线性振动特性的影响;祝效华等[4]对弯头在波动流作用下的流体力学模型和固体运动模型引入摩擦耦合因素,分析了双弯头的连接角度、弯管的壁厚和曲率半径等参数对弯管固有频率的影响。
为研究压裂泵出口高压管汇整体的振动特性,本文对3000型压裂泵的排出管汇进行了流固耦合模态分析与谐响应分析,得到高压管汇固有振动模态、流固耦合模态以及高压管汇在泵头体位移激振作用下的振动响应特性。所得结果可为现场高压管汇减振提供理论依据。
1 模态分析模态分析可以确定已知结构系统的振动特征,是进行其他动力学分析的先决条件[5]。高压管汇在受到泵头体振动激励作用以及管内高压流体作用的响应取决于管汇自身结构、约束和材料等条件。对高压管汇进行模态分析,可以得到高压管汇在非工作状态下的固有模态,以及在考虑流固耦合作用时管汇模态的变化特征。
1.1 振动模态理论高压管汇的运动微分方程如下:
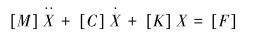
|
(1) |
式中:[M]、[C]、[K]是管汇自身的质量矩阵、阻尼矩阵以及刚度矩阵;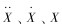
令式(1)中[C] =0、[F] =0,可得管汇的无阻尼自由振动方程为:
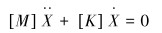
|
(2) |
设管汇的运动方程式为:
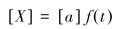
|
(3) |
式中:f(t)为管汇的运动函数,[a]是常数向量。
将式(3)带入式(2)中,并乘以[a]T得:
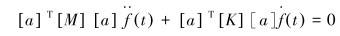
|
(4) |
对式(4)分离变量:
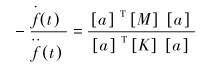
|
(5) |
令等式两边同时为常数λ,由于[M]正定,[K]正定或者半正定,故λ是特征根,令:
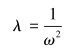
|
(6) |
式(6)中,ω是管汇的固有频率,ω≥0,令f(t) =sin(ωt+θ),则[X]= [a]sin (ωt+θ),带入式(2)可得:
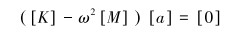
|
(7) |
式(7)存在非0解,则[a]的行列式等于0,于是有:
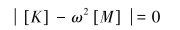
|
(8) |
式(8)是管汇振动的特征方程,通过对式(8)求解,得到管汇具有n个不同的固有频率:
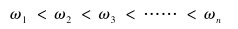
|
(9) |
由式(8)和式(9)可知,管汇本身的刚度矩阵与质量矩阵决定了管汇的固有频率。ω1为管汇基频,即管汇振动最小固有频率。
管汇的自由度数目对应主振型阶数,管汇各阶固有频率主振动的叠加构成了管汇的振动:
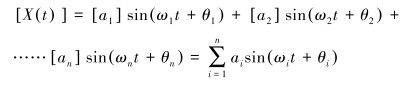
|
(10) |
式中:[ai]为管汇第i阶固有频率的主振型(i=1,2,……,n);θi为管汇第i阶固有频率主振型相位角(i=1,2,……,n)。
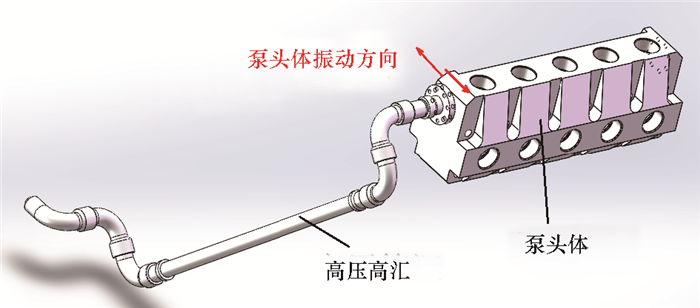
1.2 数值模型 1.2.1 几何模型与网格划分3000型压裂泵出口高压管汇几何模型如图 1所示。其中高压管线外径88.9 mm,内径64.9 mm,弯管曲率半径140 mm,材料密度7 850 kg/m3,弹性模量209 GPa,泊松比0.3。
|
| 图 1 3000型压裂泵高压管汇及泵头体几何模型 Fig.1 Geometric model of the high pressure manifold and pump head of the 3000 type fracturing pump |
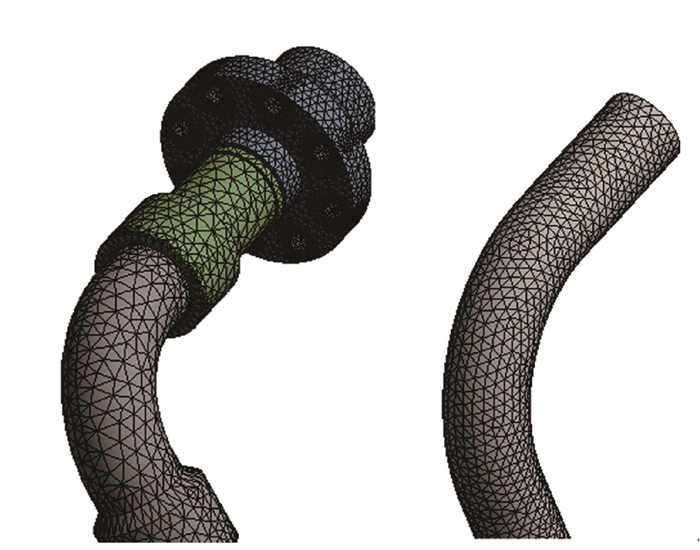
对管汇及其内部流场皆采用四面体网格划分方法,并对重要表面进行局部细化,划分后的网格模型如图 2所示。
|
| 图 2 管汇及流场网格模型 Fig.2 Grid model of the manifold and flow field |
在第4挡位工况下,对管汇以及流场模型进行网格无关性验证。当流场网格数量达到约40万个以后,随着网格数量的增加,管汇的出口流速波动非常小,管汇的各阶模态频率变化小于5%,即网格继续增加对流场的影响可忽略。因此,流场网格数量约取40万个,管汇结构网格按照与流体网格单元大小相匹配的原则进行划分,网格数量约为54万个。
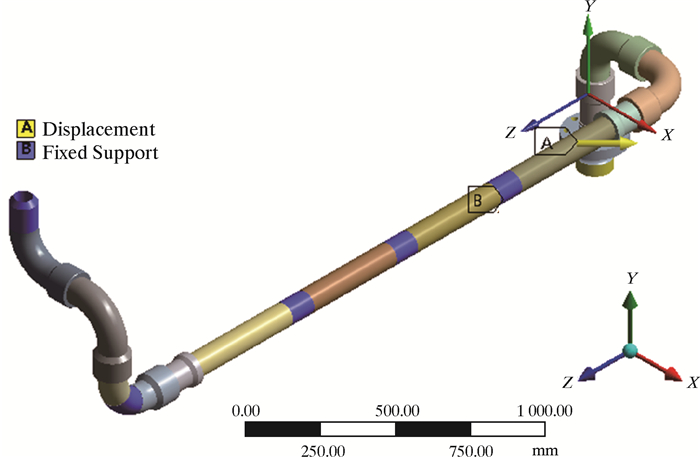
1.2.2 边界条件设置将流场出口设置为压力出口,压裂泵在各挡位工作的负载压力设置为管汇出口压力,流场进口边界设置为速度进口[6]。详细参数如表 1所示。高压管末端与地面管汇连接处为固定约束,在法兰盘螺栓孔内表面及法兰与泵头体配合圆周面施加位移载荷。压裂液密度设为1 045 kg/m3,动力黏度为0.015 Pa·s。在高压管汇的流固耦合模态分析过程中,需要对压裂液和管汇分别设置流固耦合交界面进行数据传递。
| 挡位 | 进口速度/(m·s-1) | 出口压力/MPa |
| 1 | 2.73 | 138.0 |
| 2 | 3.42 | 138.0 |
| 3 | 4.28 | 138.0 |
| 4 | 5.06 | 133.2 |
| 5 | 6.35 | 106.1 |
| 6 | 7.92 | 85.1 |
| 7 | 9.76 | 69.1 |
| 8 | 12.21 | 55.2 |
1.3 流固耦合模态分析
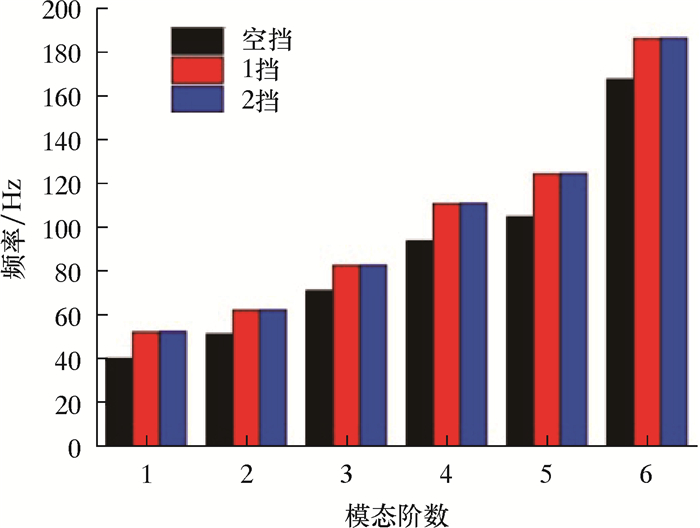
基于数值模型,计算得出空挡位模态和8个工作挡位流固耦合模态各阶频率,如表 2所示。分别提取无耦合和流固耦合作用下管汇(以第1、2挡位为例)的前6阶固有频率,如图 3所示。
| 挡位 | 1阶 | 2阶 | 3阶 | 4阶 | 5阶 | 6阶 |
| 空挡 | 40.817 | 51.908 | 71.660 | 94.392 | 105.530 | 168.140 |
| 1 | 52.569 | 62.503 | 83.058 | 111.090 | 124.820 | 186.430 |
| 2 | 52.570 | 62.503 | 83.058 | 111.090 | 124.820 | 186.430 |
| 3 | 52.570 | 62.504 | 83.059 | 111.090 | 124.820 | 186.430 |
| 4 | 52.235 | 62.180 | 82.772 | 110.600 | 124.310 | 185.870 |
| 5 | 52.273 | 60.300 | 81.079 | 107.720 | 121.330 | 182.600 |
| 6 | 48.666 | 58.782 | 79.659 | 105.370 | 118.850 | 179.970 |
| 7 | 47.382 | 57.586 | 78.495 | 103.510 | 116.820 | 177.910 |
| 8 | 46.217 | 56.518 | 77.409 | 101.830 | 114.950 | 176.080 |
|
| 图 3 有无流固耦合时的模态对比 Fig.3 The modal comparison with and without fluid-solid coupling |
由表 2可知,相对空挡位,考虑流固耦合时压裂管汇的各阶固有频率增加了11%~28%,振幅变大,管汇的振型基本相似。这是由于管内高压流体使管汇整体刚度提高,而压裂液与管汇自身的振动相互叠加,加剧了振动。因此分析高压管汇固有频率时,考虑流固耦合作用的影响很有必要。
2 谐响应分析谐响应分析能计算出结构在承受特定频率激励载荷时的振动响应,以便有目的地加固结构,避免共振的发生[7-8]。该技术的关键在于计算出结构在不同频率载荷作用下的响应值,并且得到结构的幅频特性曲线,可将其作为结构振动机理分析及减振设计的主要依据[9-11]。对高压管汇进行谐响应分析,可以计算出管汇在多种频率下的响应,从中找到峰值响应,并进一步获得峰值频率对应的位移响应,以预测高压管汇的持续动力特性,检验其能否克服共振、疲劳以及其他引起有害效果的受迫振动。
2.1 理论分析压裂泵工作时的振动通过法兰盘直接作用于管汇。若该激励的频率与管汇结构的固有频率很接近,则会发生共振,对结构的强度和寿命等将产生很大影响。取压裂车振动测试数据[6]中位移最大值16.198 mm作为激振载荷。将该复杂振动简化为简谐载荷,并分解成X向和Z向两个相位相差90°的正弦载荷施加在承载面上:
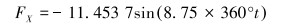
|
(11) |
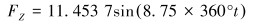
|
(12) |
管汇自身的前6阶模态频率在40.82~186.43 Hz范围内,且共振一般发生在低频段,故设定搜索频率范围为0~200 Hz、搜索步长为4 Hz能够较好地覆盖正常工况下的频率范围。
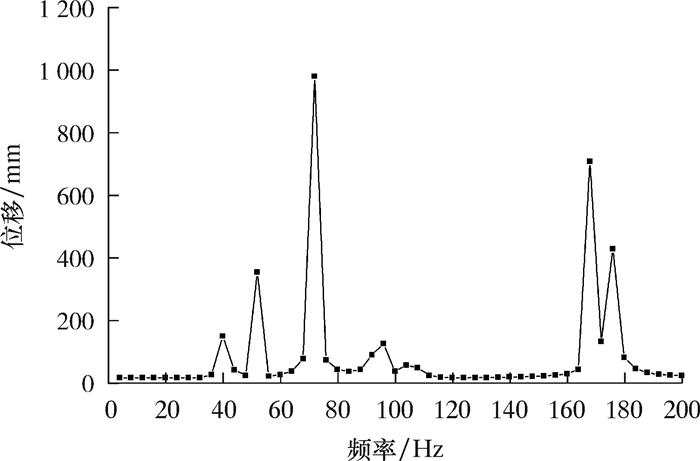
求解得到管汇振动响应结果如图 4所示。从图 4可见,在激振频率范围(0~200 Hz)内,管汇整体振动位移响应基本保持不变,约为30.25 mm,与激振位移幅值处于同一量级。但当激振频率为40、52、72、96、168和176 Hz时,振动响应出现极大值,响应幅值达到均值的数倍甚至数十倍,分别为149.28、353.75、979.50、125.37、708.18和428.17 mm。对比空管时模态分析结果可知,位移响应产生突变时的激振频率,基本与空管前6阶模态频率相对应。分析认为激振频率与管汇固有频率接近,导致管汇产生共振,且在3阶模态频率下,位移响应达到最大值,其次是6阶和2阶。其中,3阶固有频率激振下,共振时产生的位移响应达到979.5 mm,振幅异常大,这是因为在谐响应分析中,对管汇施加的约束较少,管汇整体刚度较低。本文谐响应分析中管汇位移响应值并不代表真实情况下位移响应值,仅反映该频率下振动的传递情况而非实际振动的数值。
|
| 图 4 简谐激励下管汇振动响应 Fig.4 Vibration response of manifold under harmonic excitation |
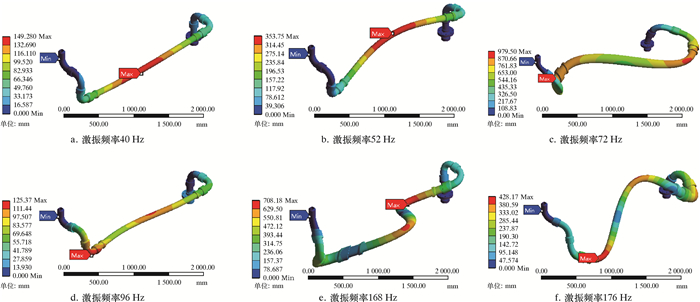
不同激振频率时位移响应云图如图 5所示。
|
| 图 5 不同激振频率时位移响应云图 Fig.5 Displacement response distribution at different excitation frequencies |
由图 5可知,在激振频率40、52、72、96、168和176 Hz的简谐载荷激振作用下,管汇最大位移响应分别出现在直管中间点、直管后端第一个弯头外侧、靠近直管两端约¼点处。建议在压裂泵工作、换挡以及启动过程中,避开上述频率,并考虑在上述位移响应最大处加约束,以高效地提高管汇整体刚度,避免管汇在外界激励下产生共振。
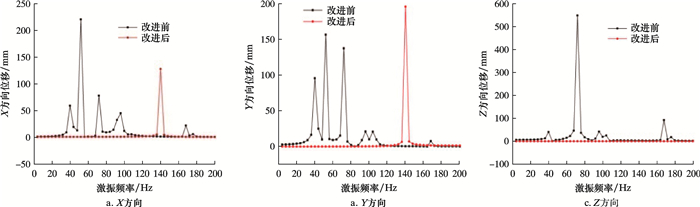
2.2 危险点处应力响应根据2.1节中结论,提出改进方案:在最大位移响应处增加固定约束,如图 6所示。计算并提取关注点在X、Y、Z方向上位移响应,并与改进前结果进行对比,如图 7和图 8所示。
|
| 图 6 改进后约束模型 Fig.6 Improved constrained model |
|
| 图 7 直管位移响应 Fig.7 Displacement response of straight pipe |
|
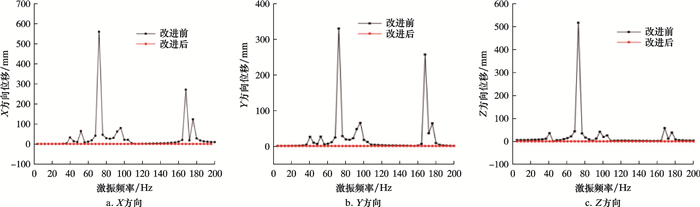
| 图 8 弯管位移响应 Fig.8 Displacement response of elbow |
由图 7可知,改进后管汇在0~200 Hz范围内简谐位移载荷激振作用下,直管位移响应改善明显。具体表现为:改进前出现多个极大位移响应峰值变为单个位移峰值。0~200 Hz内X、Y和Z方向位移响应均值分别由12.04、12.50和22.18 mm变为3.25、4.93和0.01 mm。X、Y和Z方向最大位移响应值分别由219.90、156.79及548.08 mm变为127.30、196.19及0.14 mm,整体降幅明显,其中Y方向位移响应稍有增大,但该位移值出现在高频段。位移响应极值点由低频段向高频段转移。
由图 8可知,改进后管汇在0~200 Hz范围内简谐位移载荷激振作用下,弯管位移响应改善明显。具体表现为:改进前出现多个极大位移响应峰值变为位移响应,基本保持在稳定的较低水平。0~200 Hz内X、Y和Z方向位移响应均值分别由32.97、21.38及21.01 mm变为均接近于0 mm。X、Y和Z方向最大位移响应值分别由559.67、327.79和515.86 mm变为均接近0 mm,可认为弯管在该位移载荷激振作用下几乎不发生振动。
改进后的管汇模型刚度得到有效提升,通过采用本文所述的约束方案,能有效避免管汇在低频外界激励作用下产生的共振。
3 结论(1) 相对空管模态,考虑流固耦合,压裂液的作用与管汇振动相互叠加,使压裂管汇的各阶固有频率升高,对应振幅增加11%~28%,各阶振型基本相似。
(2) 激振频率为40、52、72、96、168及176 Hz时,管汇响应出现极值,极值点频率基本与空管前6阶模态频率相对应。其中,3阶固有频率(72 Hz)激振下位移响应最大。
(3) 对危险点施加固定约束后,不仅直管与弯管的位移响应得到明显改善,管汇系统刚度得到有效提升,而且采用本文提供的约束方案,能有效避免管汇由低频外界激励作用导致的共振。
| [1] |
PAÍDOUSSIS M P, LI G X. Pipes conveying fluid:a model dynamical problem[J]. Journal of Fluids and Structures, 1993, 7(2): 137-204. DOI:10.1006/jfls.1993.1011 |
| [2] |
TUBALDI E, AMABILI M, PAÍDOUSSIS M P. Fluid-structure interaction for nonlinear response of shells conveying pulsatile flow[J]. Journal of Sound and Vibration, 2016, 371: 252-276. DOI:10.1016/j.jsv.2016.01.024 |
| [3] |
GHAYESH M H. Parametric vibrations and stability of an axially accelerating string guided by a non-linear elastic foundation[J]. International Journal of Non-Linear Mechanics, 2010, 45(4): 382-394. DOI:10.1016/j.ijnonlinmec.2009.12.011 |
| [4] |
祝效华, 曾云义, 陈波, 等. 考虑流固耦合的双弯头压裂管汇的振动特性[J]. 天然气工业, 2018, 38(1): 95-101. ZHU X H, ZENG Y Y, CHEN B, et al. Vibration characteristics of double-elbow fracturing manifold considering fluid-solid interaction[J]. Natural Gas Industry, 2018, 38(1): 95-101. |
| [5] |
李芳, 凌道盛. 工程结构优化设计发展综述[J]. 工程设计学报, 2002, 9(5): 229-235. LI F, LING D S. Survey of the development in engineering structural optimization design[J]. Journal of Engineering Design, 2002, 9(5): 229-235. DOI:10.3785/j.issn.1006-754X.2002.05.001 |
| [6] |
欧阳峰. 大功率压裂车振动特性分析与减振方法研究[J]. 内燃机与配件, 2017(7): 31-34. OUYANG F. Stucly on vibration characteristics and reduction method of fracturing truck[J]. Internal Combustion Engine & Parts, 2017(7): 31-34. DOI:10.3969/j.issn.1674-957X.2017.07.012 |
| [7] |
康国政, 阚前华, 张娟. 大型有限元程序的原理、结构与使用[M]. 成都: 西南交通大学出版社, 2008. KANG G Z, KAN Q H, ZHANG J. The principle, structure and use of large-scale finite element program[M]. Chengdu: Southwest Jiaotong University Press, 2008. |
| [8] |
凌桂龙, 丁金滨, 温正. ANSYS Workbench 13.0从入门到精通[M]. 北京: 清华大学出版社, 2012: 59-163. LING G L, DING J B, WEN Z. ANSYS Workbench 13.0 from entry to proficiency[M]. Beijing: Tsinghua University Press, 2012: 59-163. |
| [9] |
冯会民.力反馈磁悬浮控制系统的传感器性能研究[D].济南: 济南大学, 2012. FENG H M. Research on performances of sensor applied for force feedback magnetic levitation control system[D]. Jinan: University of Jinan, 2012. |
| [10] |
吴晓金, 王家序, 肖科, 等. 水润滑轴承的动态仿真分析[J]. 系统仿真学报, 2009, 21(13): 4167-4170. WU X J, WANG J X, XIAO K, et al. Dynamic simulation of water lubricated bearing[J]. Journal of System Simulation, 2009, 21(13): 4167-4170. |
| [11] |
杨明亚, 杨颖洁. 高速电主轴箱体的动态性能分析[J]. CAD/CAM与制造业信息化, 2009(5): 68-69. YANG M Y, YANG Y J. Dynamic performance analysis of high speed motorized spindle box[J]. CAD/CAM and Manufacturing Informationization, 2009(5): 68-69. |


