0 引言
冲蚀磨损通常指的是流体携带固体颗粒以一定速度冲击构件表面而发生材料损耗的现象[1]。在天然气输送过程中,高速流动的天然气携带固体砂粒冲击天然气管道弯头,随着油田开采时间的延长,出砂量增多,冲蚀累积效应越来越明显,最后可能导致管道冲蚀磨损破坏[2]。冲蚀是天然气管道弯头失效的主要原因[3-4],因此,研究天然气管道弯头在颗粒和管道结构因素影响下的冲蚀规律以及固体颗粒在管道中的运动规律意义重大[5]。
国内外不少学者已经对气固两相流弯管冲蚀开展了大量的研究工作。其中美国Tulsa大学的A.T.J.BOURGOYNE[6]通过试验研究了气体携带砂粒冲击靶材及标准弯头的侵蚀结果,并通过安装在材料表面的敏感电阻探针来测量侵蚀结果。英国石油公司研究了高压天然气携带砂粒冲击下不同材料弯管的最大冲蚀率[7]。崔钺等[8]进行了气固冲蚀和CO2腐蚀共同作用下弯管失效分析。王思邈等[9]使用4种冲蚀预测模型模拟弯管在气固两相流下的冲蚀,并与试验数据对比分析了不同冲蚀模型的适用性。彭文山等[10]开展了气固两相流下弯管内固体颗粒轨迹分析。黄勇等[11]对气固两相流冲蚀弯管结构进行了优化分析。以上弯管冲蚀研究多为特定工况下的定量冲蚀研究,对于固体颗粒参数变化和弯管结构参数变化条件下的弯管冲蚀规律及最大冲蚀位置的研究还不完善。
为此,笔者基于CFD软件Fluent,对弯管进行网格无关性分析和入口直管段长度分析来确定最佳分析模型,经过分析选用Oka冲蚀预测模型和Forder壁面恢复模型来计算弯管冲蚀,同时分析了颗粒参数和管道结构参数对弯管冲蚀的影响,研究了颗粒直径和管径比对弯管最大冲蚀位置的影响。所得结果对管道设计和工程实际安全运营具有一定的指导意义。
1 理论模型及控制方程 1.1 连续相模型流体在流动过程中遵循质量守恒定律、动量守恒定律及能量守恒定律。计算流场采用N-S方程,连续性方程和动量方程表示如下:
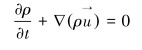
|
(1) |
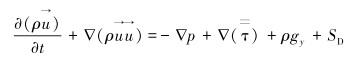
|
(2) |
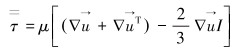
|
(3) |
式中: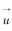

笔者使用标准的k-ε湍流模型,表征流体速度波动变化的湍流动能k方程和湍流动能耗散率ε方程表示为:
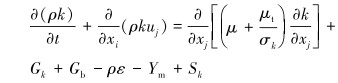
|
(4) |
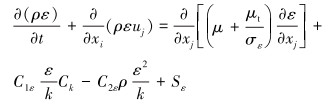
|
(5) |
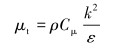
|
(6) |
式中:k为湍流动能,J;μt为湍流黏度,Pa·s;σk为湍动能对应的普朗特数,取为1.0;Gb为浮力影响引起的湍动能,J;Gk为平均速度引起的湍动能,J;Ym为湍流脉动对耗散率的作用;ε为湍流耗散率,W/m3;σε为湍动能耗散率对应的普朗特数,取为1.3;C1ε和C2ε为经验常数,取值分别1.44和1.92;Cμ为经验系数,取为0.09;Sk和Sε为用户定义源项。
1.2 离散相模型离散相颗粒在流体中的运动通过牛顿第二定律来确定。拉格朗日坐标系下粒子的运动受力方程表示如下:
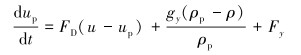
|
(7) |
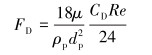
|
(8) |
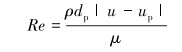
|
(9) |
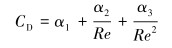
|
(10) |
式中:up为砂粒速度,m/s;ρp为砂粒密度,kg/m3;Fy为其他方向的作用力,N;CD为拖曳力系数。
式(10)中的常数α1、α2和α3取值见参考文献[12]。
1.3 冲蚀磨损模型国内外已经有大量学者基于试验给出冲蚀的经验、半经验模型。Y.I.OKA等[13]在2005年提出的冲蚀预测模型将材料塑性变形效应积累和颗粒对材料微切削效应积累考虑在内,模型充分考虑了碰撞角度、速度、粒径及材料硬度等的影响,因此具有较高的可信度。笔者将使用该模型进行冲蚀预测,模型表示如下:
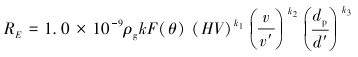
|
(11) |
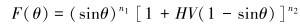
|
(12) |
式中:RE为冲蚀速率,kg/(m2·s);ρg为弯管的密度,kg/m3;HV为弯管的维式硬度;v为颗粒速度,m/s;dp为颗粒粒径,μm;θ为颗粒对管壁的冲击角,rad;f(θ)为冲击角函数;v′为参考冲蚀速率,m/s;d′为参考冲蚀深度,μm;k、k1、k2、k3、n1、n2为常数。
1.4 颗粒壁面碰撞模型颗粒与管道壁面发生碰撞后速度大小和方向都会发生改变。使用壁面恢复系数来表示颗粒碰撞后速度方向的变化。常用模型有Forder模型[14]和Tabakoff[15]模型,Tabakoff模型的冲击材料为高硬度铝,不适用于本文分析。Forder颗粒壁面碰撞模型表示如下:
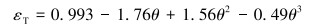
|
(13) |
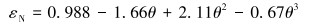
|
(14) |
式中:εT代表切向方向的恢复系数,εN代表法向方向的恢复系数。
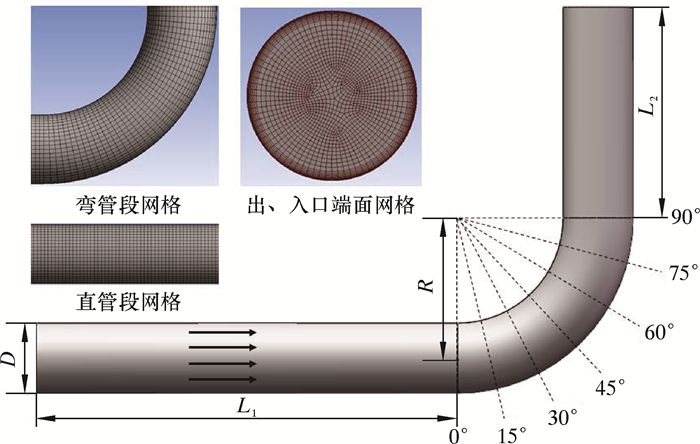
2 仿真模型 2.1 物理模型和网格划分选取天然气输气管道中含直管入口段-弯曲段-直管出口段的部分进行分析,采用扫略方式划分网格。为考虑管壁处黏性底层的影响,使用inflation将边界层细化10层,设置生长因子为1.2。弯曲管道几何模型和网格模型如图 1所示。图 1中,L1为入口直管段长度,L2为出口直管段长度,管道内径为D,弯管半径为R。
|
| 图 1 弯曲管道几何模型和网格模型 Fig.1 Geometry model and mesh model of the bend pipe |
2.2 边界条件
气相为连续相,砂粒为离散相。对连续相而言,采用标准k-ε湍流模型,近壁区域采用标准壁面函数处理。入口采用速度入口边界,出口采用自由出流边界,壁面采用标准壁面边界。离散相通过injection注射,粒子喷射性质选为表面surface喷射,设置入射面为inlet,粒子类型设置为尺寸均匀的石英石(密度为2 650 kg/m3)。分别设置粒子的注入速度、颗粒直径和质量流量,其中粒子的注射速度与连续相的流入速度相同。在DPM选项卡中设置入口和出口采用escape模型,固体颗粒与壁面碰撞时采用reflect壁面反弹模型。
动量和湍动能采用二阶迎风离散格式,求解器选用常用的半隐式SIMPLE算法,该算法在求解湍流问题时可以得到较好的收敛计算结果。初始化选择标准初始化方法,并设置为从入口初始化。
2.3 网格适应性分析网格形式和质量直接影响计算精度和计算量大小,进行网格适应性分析能够在有效减小计算量的情况下获得较高的计算精度。这里分析入口速度为10 m/s,质量流量为0.01 kg/s,颗粒直径为0.1 mm,入口直管段L1长度为6D,出口直管段L2长度为3D时。不同网格密度下弯管的冲蚀模拟结果如表 1所示。
| 网格尺寸/mm | 网格数量 | 网格变化/% | 冲蚀率/ (kg·m-2·s-1) | 冲蚀率变化/% |
| 8 | 93 642 | — | 2.84×10-6 | — |
| 7 | 125 760 | 34.2 | 2.56×10-6 | 9.800 |
| 6 | 192 324 | 52.9 | 2.51×10-6 | 1.150 |
| 5 | 311 202 | 61.8 | 2.50×10-6 | 0.398 |
从表 1可以看出,随着网格的加密,最大冲蚀速率不断变化,但是基本在2.84×10-6~2.50×10-6 kg/(m2·s)之间。从网格单元变化来看,网格每细化1 mm,网格数量逐渐增大,计算量逐渐增加,当网格尺寸从8 mm依次变到5 mm时,最大冲蚀速率依次为2.84×10-6、2.56×10-6、2.51×10-6、2.50×10-6 kg/(m2·s-1),变化量依次为9.800%、1.150%及0.398%。当网格尺寸从6 mm变为5 mm时,网格数量增加了61.8%,最大冲蚀速率误差为0.398%。为减小计算量,选用网格尺寸为6 mm进行分析可以在保证计算精度的情况下有效减小计算量。
2.4 出、入口直管段长度确定为使流入弯管内的流动充分发展为稳定流,笔者对比了网格尺寸为6 mm时,入口直管段L1长度分别为4D、5D、6D及7D时弯管的冲蚀情况,结果如表 2所示。
| L1 | L2 | 网格数量 | 网格变化/% | 冲蚀率/ (kg·m-2·s-1) | 冲蚀变化/% |
| 4D | 2.0D | 143 752 | — | 2.99×10-6 | — |
| 5D | 2.5D | 173 595 | 20.7 | 2.60×10-6 | 13.1 |
| 6D | 3.0D | 192 324 | 10.8 | 2.51×10-6 | 3.4 |
| 7D | 3.5D | 195 510 | 1.6 | 2.49×10-6 | 0.7 |
从表 2可以看出,随着出、入口直管段长度变化,弯管最大冲蚀速率也不断变化,但是基本在2.99×10-6~2.49×10-6 kg/(m2·s)之间。直管段长度增加会导致网格数量增多进而增加计算量,当直管段长度L1从4D依次变到7D时,最大冲蚀速率依次为2.99×10-6、2.60×10-6、2.51×10-6及2.49×10-6 kg/(m2·s),变化量依次为13.1%、3.4%和0.7%。当直管段长度L1超过6D后,网格数量和冲蚀速率变化较小,可以认为选用直管段长度L1为6D进行分析能够在保证计算精度的情况下有效减小计算量。
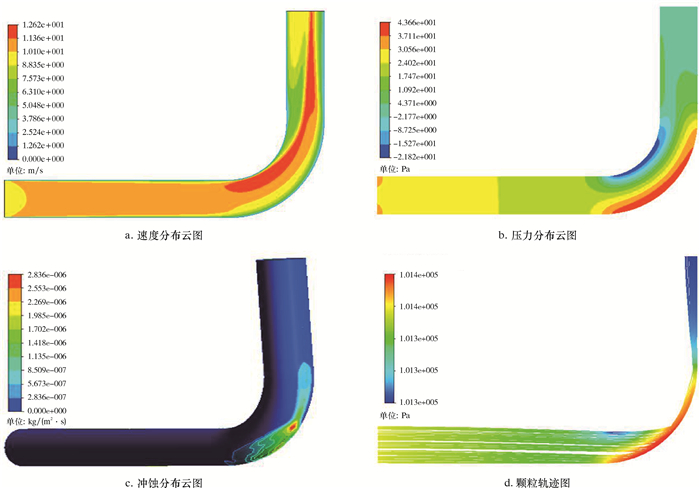
3 冲蚀参数化分析及结果讨论 3.1 仿真结果分析图 2是气固两相流速度为10 m/s、颗粒直径为100 μm、颗粒质量流量为0.005 kg/s、网格尺寸为8 mm、L1为6D、L2为3D时的仿真结果图。
|
| 图 2 弯曲管道冲蚀仿真结果 Fig.2 Erosion simulation results of the bend pipe |
从图 2a和图 2b可以看出,弯管段有最大速度和最高压力,弯管段外侧速度较小而压力较高,内侧速度较大而压力较低。这是因为流体流经弯管时流体沿弯管方向产生离心力,进而对弯管外侧产生较大挤压。离心力对弯管内侧壁的牵引作用会使流体对管壁的压力减小,使弯管内侧的比压能转化为流体动能,增大了流体的速度。从图 2c可以看出,最大冲蚀位置发生在弯管外侧壁面上,原因是从水平直管段流过的颗粒直接冲击弯管外侧壁面。从图 2d可以看出,粒子在与弯管外侧壁面发生碰撞后,固体颗粒被高速流体携带着沿流线方向运动,颗粒不易穿过流线与竖直管段发生第二次碰撞,颗粒沿着弯管外侧和竖直管道壁面滑移,因此竖直管段内侧壁面没有发生冲蚀,而外侧壁面则因为颗粒的滑移磨损而有较小的冲蚀。
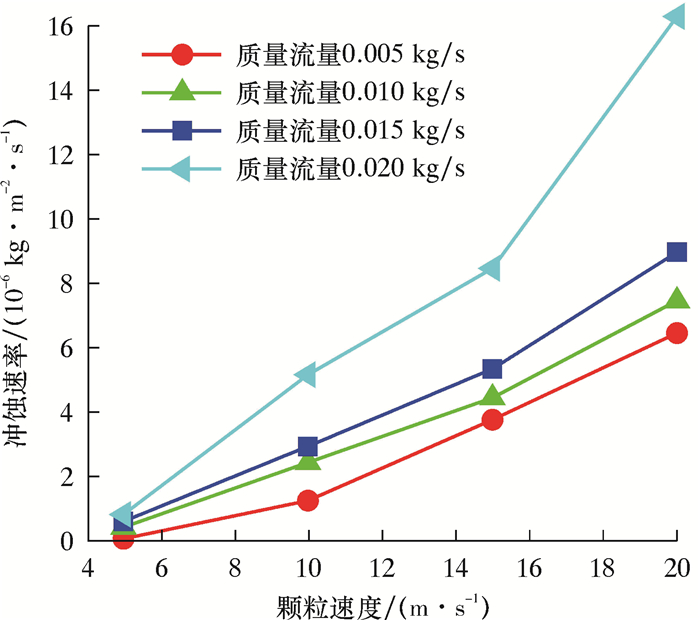
3.2 固体颗粒参数化分析为得到固体颗粒参数对冲蚀的影响,笔者分析了固体颗粒直径、速度及质量流量等参数对弯管冲蚀的影响。图 3是气固两相流颗粒直径为100 μm,颗粒速度为5、10、15及20 m/s,颗粒质量流量为0.005、0.010、0.015及0.020 kg/s时的冲蚀速率规律图。
|
| 图 3 不同质量流量下颗粒速度-冲蚀速率关系图 Fig.3 Relationship between particle velocity and erosion rate under different mass flow rates |
从图 3可以看出:最大冲蚀速率随颗粒速度的增大而呈指数增大,质量流量为0.010 kg/s时,冲蚀速率从颗粒速度为5 m/s时的5.18×10-6 kg/(m2·s)增加到20 m/s时的6.50×10-6 kg/(m2·s);冲蚀速率随质量流量的增大而增大,颗粒速度为10 m/s时,冲蚀速率从颗粒质量流量为0.005 kg/s时的1.34×10-6 kg/(m2·s)增加到0.020 kg/s时的5.22×10-6 kg/(m2·s)。速度对冲蚀率的影响较大,主要是因为速度越大,将有更多的动能转化为对管壁的比压能,同时会产生更大的管壁剪切应力,剥离内壁层加重冲蚀[16]。
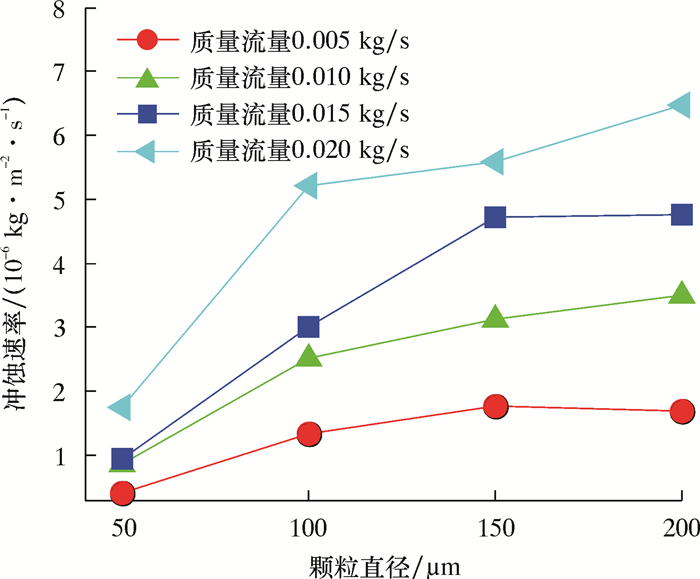
图 4是气固两相流速度为10 m/s,颗粒直径为50、100、150和200 μm,颗粒质量流量为0.005、0.010、0.015及0.020 kg/s时的冲蚀速率规律图。
|
| 图 4 不同质量流量下颗粒直径-冲蚀速率关系图 Fig.4 Relationship between particle diameter and erosion rate under different mass flow rates |
从图 4可以看出:冲蚀速率随着颗粒直径的增大而增大,颗粒质量流量为0.010 kg/s时,冲蚀速率从颗粒直径为50 μm时的8.55×10-6 kg/(m2·s)增加到200 μm时的3.51×10-6 kg/(m2·s);冲蚀速率随质量流量的增大而增大,颗粒直径为100 μm时,冲蚀速率从颗粒质量流量为0.005 kg/s时的1.34×10-6 kg/(m2·s)增加到0.020 kg/s时的5.22×10-6 kg/(m2·s);当颗粒直径达到150 μm后,冲蚀速率增加较慢,主要是由于颗粒增大到一定大小后,颗粒与流体之间的相互耦合作用使得最后的冲蚀速率趋于平稳。
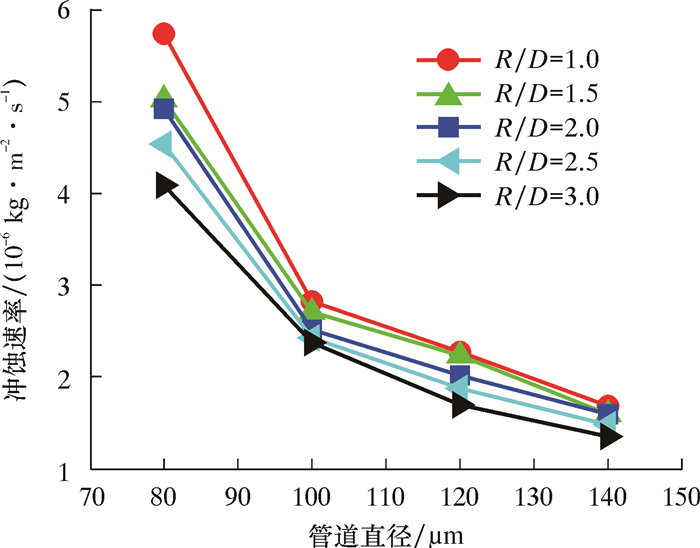
3.3 弯管结构参数化分析图 5是气固两相流速度为10 m/s,质量流量为0.010 kg/s,颗粒直径为100 μm,管道直径为80、100、120及140 mm,管径比为1.0、1.5、2.0、2.5及3.0时的弯管冲蚀速率规律图。
|
| 图 5 不同管径比下管道直径-冲蚀速率关系图 Fig.5 Relationship between pipe diameter and erosion rate under different pipe diameter ratios |
由图 5可以看出:冲蚀速率随着管道直径的增大而减小,管径比为2.0时,冲蚀速率从管道直径为80 mm时的4.92×10-6 kg/(m2·s)减小到140 mm时的1.47×10-6 kg/(m2·s),原因是大管径的弯管具有较大内壁面积,单位面积上受到离散颗粒的碰撞冲击数量减小,导致冲蚀速率减小;管道冲蚀速率随管径比的增大而不断减小,管道直径为100 mm时,冲蚀速率从管径比为1.0时的2.82×10-6 kg/(m2·s)减小到管径比为3.0时的2.38×10-6 kg/(m2·s),主要原因是随着管径比增大,弯管内流动趋于平缓,固体颗粒对管壁的冲击减弱,因而冲蚀速率降低。
4 弯管最大冲蚀位置分析S.M.EIBEHERY等[17]研究发现,管径比是影响弯管最大冲蚀位置重要的因素。彭文山等[10]的研究表明,固体颗粒直径在100~150 μm时冲蚀规律明显不同,可能存在最大冲蚀位置。笔者主要分析这两种因素对最大冲蚀位置的影响。
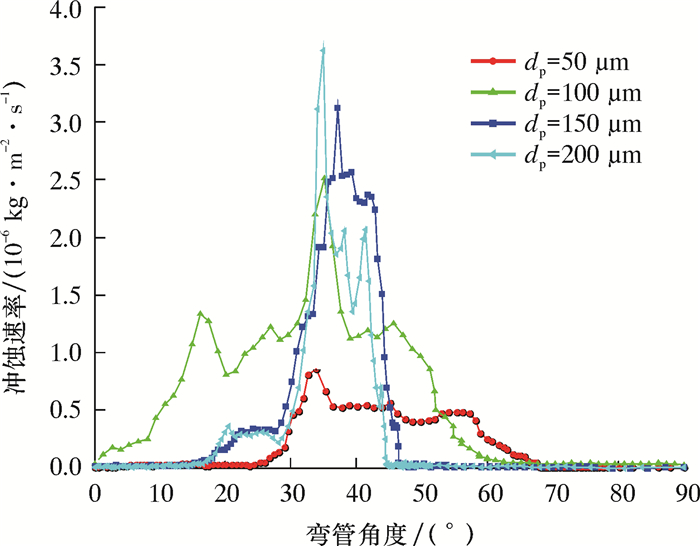
4.1 颗粒直径对最大冲蚀角度的影响图 6是气固两相流速度为10 m/s,质量流量为0.010 kg/s,管径比为2.0,颗粒直径为50、100、150及200 μm时,弯管外侧与中心对称XOY面交线上不同角度的冲蚀速率图。由图 6可以看出,随着颗粒直径变大,最大冲蚀速率不断增大,但是颗粒直径大小对最大冲蚀位置几乎无影响,颗粒直径为50、100、150及200 μm时,最大冲蚀角度均在32°~35°之间。
|
| 图 6 不同颗粒直径下弯管外侧壁面与XOY平面交线上不同角度的冲蚀速率图 Fig.6 Erosion ratio of the long side bend pipe surface crossing the XOY plane under different angles and different particle diameters |
4.2 管径比对对最大冲蚀角度的影响
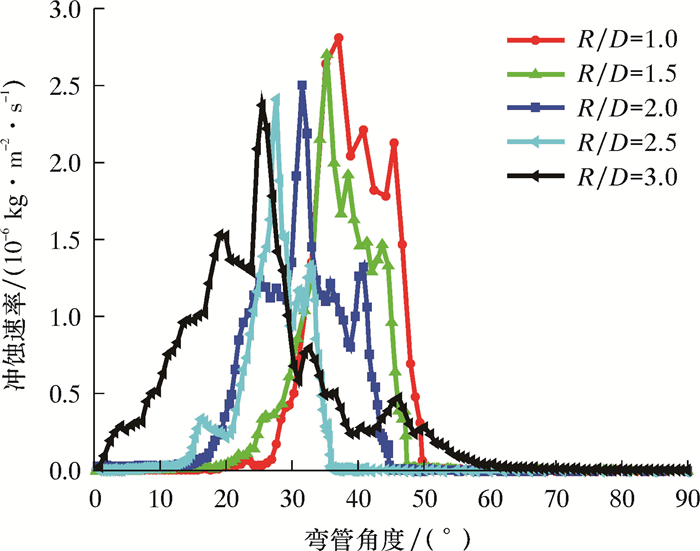
图 7是气固两相流速度为10 m/s,质量流量为0.010 kg/s,颗粒直径为100 μm,管道直径为100 mm,管径比为1.0、1.5、2.0、2.5及3.0时,弯管外侧与中心对称XOY面上不同角度的冲蚀速率图。
|
| 图 7 不同管径比下弯管外侧壁面与XOY平面交线上不同角度的冲蚀速率图 Fig.7 Erosion ratio of the long side bend pipe surface crossing the XOY plane under different angles and pipe diameter ratios |
由图 7可知,随着管径比的增大,冲蚀速率不断减小,最大冲蚀角不断减小。当管道直径为100 mm时,管径比为1.0、1.5、2.0、2.5及3.0时的最大冲蚀角分别为36°、34°、32°、26°及24°,角度变化较大,主要原因是随着管径比增大,弯管的弯曲长度增大,从水平直管段流入冲击到弯管外侧壁面的夹角减小。
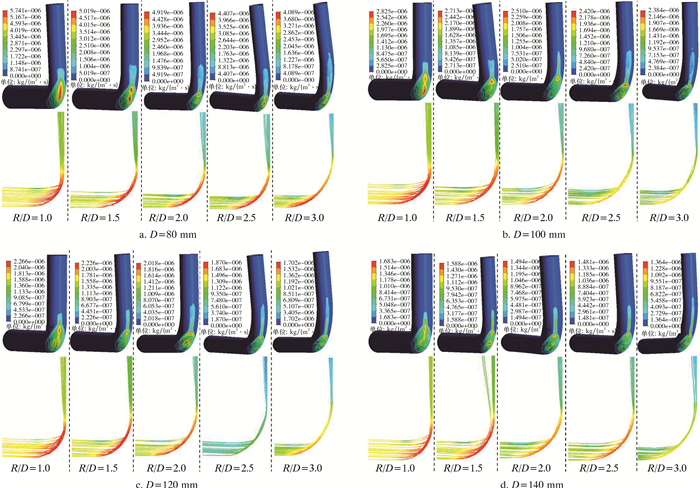
4.3 不同管径比下最大冲蚀位置与颗粒轨迹从以上分析可以看出,管径比是影响弯管最大冲蚀位置显著的因素。为深入研究管径比影响最大冲蚀位置的深层原因,这里采用Lagrangian跟踪法获取不同管径比下颗粒的轨迹。图 8是不同管道直径和不同管径比下弯管的冲蚀速率云图和粒子轨迹图。
|
| 图 8 不同管径比下弯管冲蚀云图和粒子轨迹图 Fig.8 Erosion distribution and particle trajectories of bend pipe under different pipe diameter ratios |
由图 8可以看出:不同直径和管径比弯管的最大冲蚀位置均发生在弯管外侧;当弯管直径相同时,随着管径比的增大,弯管外侧最大冲蚀速率和最大冲蚀速率面积区域逐渐减小;冲蚀最严重区域逐渐由弯管中心外侧向水平直管段和弯管连接处外侧转移;当管径比相同时,随着管道直径的增大,弯管外侧最大冲蚀速率和最大冲蚀速率面积区域逐渐减小;不同管道直径和管径比下,固体颗粒均没有与竖直管段发生第二次碰撞,而是沿着弯管外侧和竖直管道壁面滑移到竖直直管段出口。
从粒子轨迹图可以看出,随着管径比不断增大,弯管壁上直接冲击区域和滑移冲击区域不断下移,这就解释了最大冲蚀角度随着管径比增大而减小的现象。
5 结论(1) 通过网格无关性分析和出入口直管段长度分析,发现网格大小为6 mm、入口直管段长度为6D时能够在有效减小仿真计算量的情况下保证计算精度。
(2) 对颗粒速度、质量流量及直径对弯管冲蚀速率的影响进行了参数化分析,发现3种参数的增大均会加大管道冲蚀速率。颗粒速度对冲蚀速率的影响较大,二者呈指数关系,冲蚀速率随质量流量的增加比较均匀,当颗粒直径达到一定大小后,冲蚀速率增加较慢。
(3) 对管道直径、管径比对弯管冲蚀速率的影响进行了参数化分析,发现两种参数的增大均会减小管道冲蚀速率,其中管径比对冲蚀速率的影响较大,二者呈指数关系。
(4) 分析了管道直径及管径比对弯管最大冲蚀速率位置的影响,发现颗粒直径基本不影响最大冲蚀位置,而最大冲蚀角度随着管径比的增大而减小。
(5) 可以根据工况实际需求,改变管道入口流体参数,控制砂粒直径和质量流量以有效减轻天然气管道冲蚀。
| [1] |
郑玉贵, 姚治铭, 柯伟. 流体力学因素对冲刷腐蚀的影响机制[J]. 腐蚀科学与防护技术, 2000, 12(1): 36-40. ZHENG Y G, YAO Z M, KE W. Review on the effects of hydrodynamic factors on erosion corrosion[J]. Corrosion Science and Protection Technology, 2000, 12(1): 36-40. DOI:10.3969/j.issn.1002-6495.2000.01.010 |
| [2] |
韩宝坤, 蒋相广, 刘泽坤, 等. 中低压天然气管道弯头处泄漏流场和声场模拟仿真[J]. 油气储运, 2018, 37(11): 1259-1265. HAN B K, JIANG X G, LIU Z K, et al. Analog simulation on flow field and sound field of leakage at the elbows of middle and low pressure natural gas pipelines[J]. Oil&Gas Storage and Transportation, 2018, 37(11): 1259-1265. |
| [3] |
曹学文, 李星標, 樊茵, 等. 固体颗粒冲蚀理论与试验研究进展[J]. 油气储运, 2018, 37(11): 1259-1265. CAO X W, LI X B, FAN Y, et al. Progress of theory and test studies on the erosion of solid particles[J]. Oil&Gas Storage and Transportation, 2018, 37(11): 1259-1265. |
| [4] |
李铁山. 输气管道弯头开裂的原因探讨和预防[J]. 石油工程建设, 1998(6): 51-54. LI T S. Cause discussion and precaution of elbow bend cracking in gas transportation pipeline[J]. Petroleum Engineering Construction, 1998(6): 51-54. |
| [5] |
祝效华, 曾云义, 陈波, 等. 考虑流固耦合的双弯头压裂管汇的振动特性[J]. 天然气工业, 2018, 38(1): 95-101. ZHU X H, ZENG Y Y, CHEN B, et al. Vibration characteristics of double-elbow fracturing manifold considering fluid-solid interaction[J]. Natural Gas Industry, 2018, 38(1): 95-101. |
| [6] |
BOURGOYNE A T J. Experimental study of erosion in diverter systems due to sand production[C]. SPE/AIDC Drilling Conference.[S.l.]: Society of Petroleum Engineers, 1989.
|
| [7] |
CHEN X H, MCLAURY B S, SHIRAZI S A. Application and experimental validation of a computational fluid dynamics (CFD)-based erosion prediction model in elbows and plugged tees[J]. Computer and Fluids, 2004, 33(10): 1251-1272. DOI:10.1016/j.compfluid.2004.02.003 |
| [8] |
崔钺, 兰惠清, 何仁洋, 等. 冲蚀作用下CO2分压对集输气管线内腐蚀的影响规律:以大庆油田徐深6集气站集输管线为例[J]. 天然气工业, 2013, 33(2): 128-132. CUI Y, LAN H Q, HE R Y, et al. Effect of CO2 partial pressure on the corrosion in flow and transport lines under the erosion action:a case study from the Xushen-6 Gas Station in the Daqing Oil Field[J]. Natural Gas Industry, 2013, 33(2): 128-132. |
| [9] |
王思邈, 刘海笑, 张日, 等. 海底管道沙粒侵蚀的数值模拟及侵蚀公式评价[J]. 海洋工程, 2014, 32(1): 49-59. WANG S M, LIU H X, ZHANG R, et al. Numerical simulations of sand erosion in pipelines and evaluations of solid particle erosion equations[J]. The Ocean Engineering, 2014, 32(1): 49-59. DOI:10.3969/j.issn.1005-9865.2014.01.007 |
| [10] |
彭文山, 曹学文. 基于气-固双向耦合的输气管道最大冲蚀角度预测[J]. 天然气工业, 2016, 36(2): 110-118. PENG W S, CAO X W. Prediction on the maximum erosion angle of gas pipelines based on the gas-solid bidirectional coupling[J]. Natural Gas Industry, 2016, 36(2): 110-118. |
| [11] |
黄勇, 王雪东, 王京印, 等. 基于CFD的排屑管路弯头局部冲蚀磨损研究[J]. 石油机械, 2014, 42(2): 6-9. HUANG Y, WANG X D, WANG J Y, et al. CFD-based research on the local erosion and abrasion of cutting conveying pipeline elbow[J]. China Petroleum Machinery, 2014, 42(2): 6-9. DOI:10.3969/j.issn.1001-4578.2014.02.002 |
| [12] |
MORSI S A, ALEXANDER A J. An investigation of particle trajectories in two-phase flow systems[J]. Journal of Fluid Mechanics Digital Archive, 1972, 55(2): 193-208. |
| [13] |
OKA Y I, OKAMURA K, YOSHIDA T. Practical estimation of erosion damage caused by solid particle impact. Part 1:effects of impact parameters on a predictive equation[J]. Wear, 2005, 259(1/2/3/4/5/6): 95-101. |
| [14] |
FORDER A, THEW M, HARRISON D. A numerical investigation of solid particle erosion experienced within oilfield control valves[J]. Wear, 1998, 216(2): 184-193. DOI:10.1016/S0043-1648(97)00217-2 |
| [15] |
GRANT G, TABAKOFF W. Erosion prediction in turbomachinery resulting from environmental solid particles[J]. Journal of Aircraft, 1975, 12(5): 471-478. DOI:10.2514/3.59826 |
| [16] |
李洋, 曾祥国, 肖雨果, 等. 气液两相流在油气弯管处冲刷腐蚀的数值模拟[J]. 石油机械, 2015, 43(12): 104-108. LI Y, ZENG X G, XIAO Y G, et al. Numerical simulation of oil and gas elbow erosion corrosion under gas-liquid two-phase flow[J]. China Petroleum Machinery, 2015, 43(12): 104-108. |
| [17] |
EIBEHERY S M, HAMED M H, IBRAHIM K A, et al. CFD evaluation of solid particles erosion in curved ducts[J]. Journal of Fluids Engineering, 2010, 132(7): 071303. DOI:10.1115/1.4001968 |



