0 引言
由于原油管道内的蜡沉积物强度较大,所以常用传统机械清管器对其进行清理[1-5]。传统机械清管器主要由皮碗和骨架组成,按照驱动方式和清蜡方式可以分为直板皮碗清管器和碟形皮碗清管器[6]。皮碗作为传统机械清管器重要的清蜡部件,其与管壁的接触应力决定皮碗清管器的清蜡效果。随着智能清管器的不断发展,碟形皮碗在密封和驱动方面发挥的作用越来越大,要求在满足密封与驱动的条件下尽可能地减小皮碗与管壁之间的摩擦力。
前人利用ABAQUS有限元分析软件对直板皮碗和碟形皮碗的接触性能进行了研究[7-8],得出了皮碗过盈量、厚度与皮碗接触应力的关系。但是关于碟形皮碗唇部弯曲角度对接触应力的影响却鲜有研究。为此,本文利用ABAQUS对不同唇部弯曲角度碟形皮碗的接触应力进行分析,探究皮碗过盈量、厚度和所受压差对接触应力的影响,以期为清管器密封皮碗和驱动皮碗的选择提供理论指导。
1 力学分析为了保证清管器在管道中的密封性,皮碗相对管道内径会有一定的过盈量。皮碗材料通常采用聚氨酯橡胶,该橡胶具有一定的弹性,当皮碗与管壁过盈接触时会发生弹性变形。但聚氨酯橡胶是一种非线性材料,因此对其进行定量分析有一定的难度。
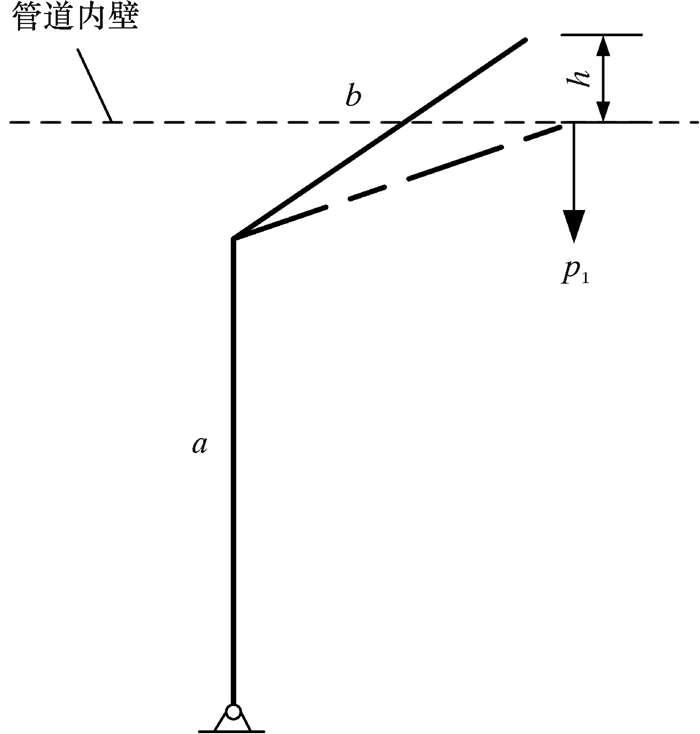
为了方便对皮碗的受力进行描述,将未受压差作用的皮碗简化为图 1所示模型。图 1中的a部分为皮碗的基座。由于皮碗通过法兰连接安装在清管器骨架上,可以认为a部分不会发生变形。图 1中的b部分为皮碗的唇部。由于皮碗与管道内壁为过盈接触,皮碗的唇部会发生压缩变形,压缩量如图 1中h所示。压缩后,皮碗的唇部位置位于图 1中虚线处,管壁对皮碗唇部的作用力如图 1中p1所示。定义a、b之间的夹角为唇部弯曲角度。
|
| 图 1 未受压差作用时皮碗受力模型 Fig.1 The force model of the cup when the pressure difference is not applied |
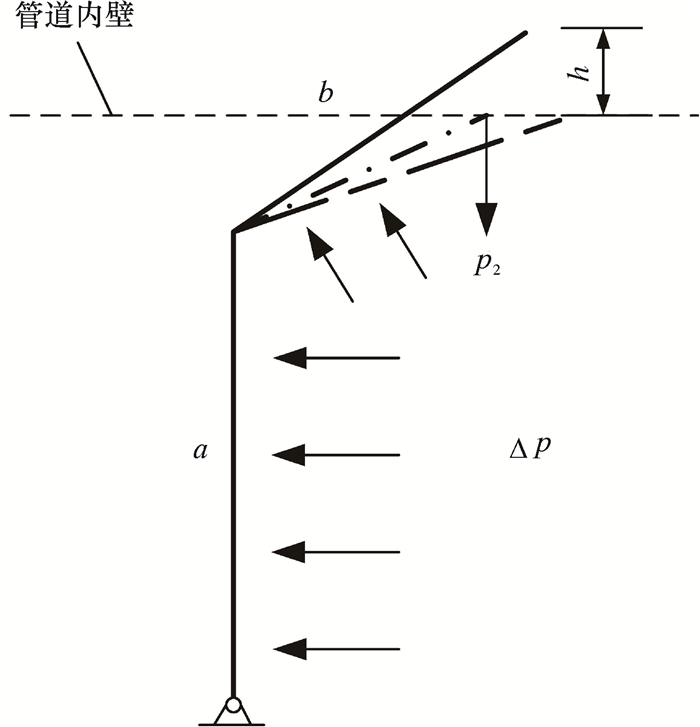
图 2为受压差作用时皮碗的受力模型。在压差作用下,皮碗唇部发生进一步的变形,受到的管壁挤压力变为p2。
|
| 图 2 受压差作用时皮碗受力模型 Fig.2 The force model of the cup when the pressure difference is applied |
为了对皮碗进行力学分析,需要对其受力做进一步简化,简化后皮碗受力如图 3所示。
|
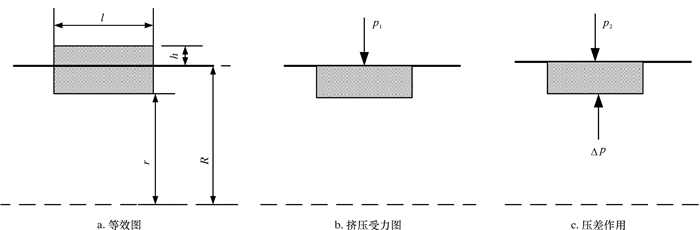
| 图 3 皮碗受力简图 Fig.3 Forces on the cup |
图 3a为皮碗受力等效图,图 3b为皮碗被管道内壁挤压受力图,图 3c为压差作用在皮碗上的受力图。假设皮碗处于弹性变形范围内,且变形较小,这样就可以利用弹性力学公式进行计算。
管道刚度远大于皮碗刚度,因此可以将管道看成刚体,皮碗可以看作一个圆筒,则由弹性力学公式可得:
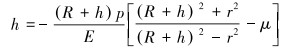
|
(1) |
式中:h为皮碗压缩量,mm;R为管道内径,mm;E为皮碗弹性模量,Pa;p为管壁对皮碗的挤压力,Pa;r为皮碗内径,mm;μ为皮碗泊松比。
由式(1)可得p1的表达式为:
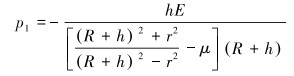
|
(2) |
当压差作用在皮碗上时,可得p2的表达式为:
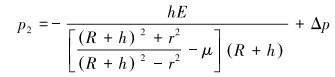
|
(3) |
在压差作用下,单个皮碗所受到的摩擦力可由下式表示:
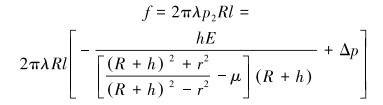
|
(4) |
式中:f为皮碗受到的摩擦阻力,N;l为皮碗与管道内壁的接触长度,mm;λ为皮碗与管道内壁之间的摩擦因数;Δp为压差,Pa。
综上所述,清管器皮碗与管壁间的摩擦力与皮碗厚度、过盈量、接触长度、所受压差以及摩擦因数有关。
2 有限元模型虽然之前已经有许多研究人员利用有限元法对以橡胶为材料的结构进行了有限元计算[9-13],但均无法对皮碗进行定量计算,因此笔者使用有限元分析软件ABAQUS分析唇部弯曲角度对接触应力的影响。
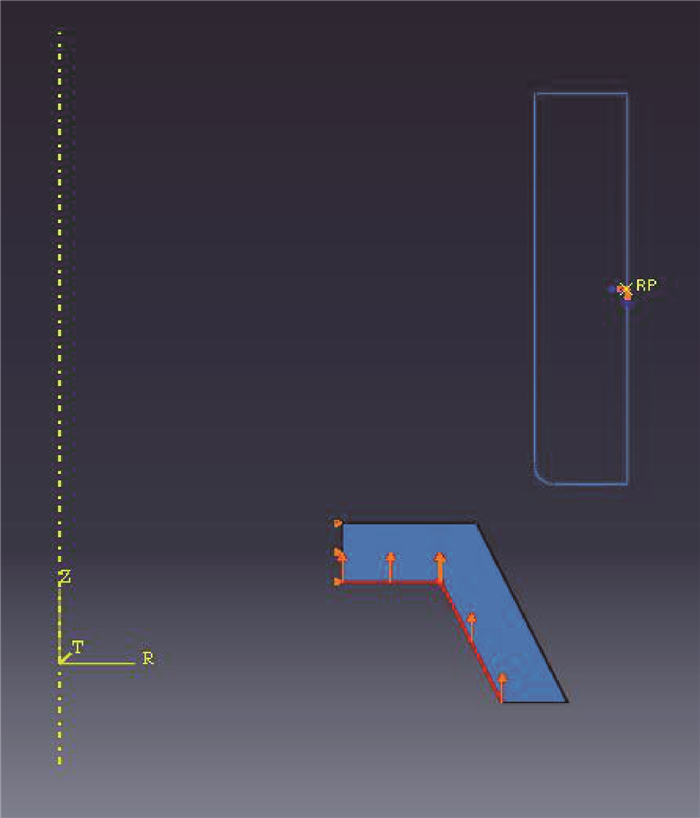
将皮碗与管道简化为二维轴对称模型[14](见图 4)。以DN508管道为例,设置唇部弯曲角度α的范围为105°~120°,间隔3°。将管道设置为轴对称解析刚体,皮碗设置为轴对称可变形体,采用CAX4H杂交单元,皮碗与管道内壁的摩擦采用库伦模型,摩擦因数设置为0.12。对管道进行全约束,约束皮碗X方向的位移,分两步对皮碗施加Y方向的位移,使其逐渐与管壁接触。将皮碗与管壁接触的初始位置圆角化,有利于皮碗与管道内壁接触,使计算收敛。由于橡胶的非线性,使用两参数的Mooney-Rivlin本构模型[15]。
|
| 图 4 有限元模型 Fig.4 Finite element model |
3 计算结果分析 3.1 不同过盈量时接触应力分析
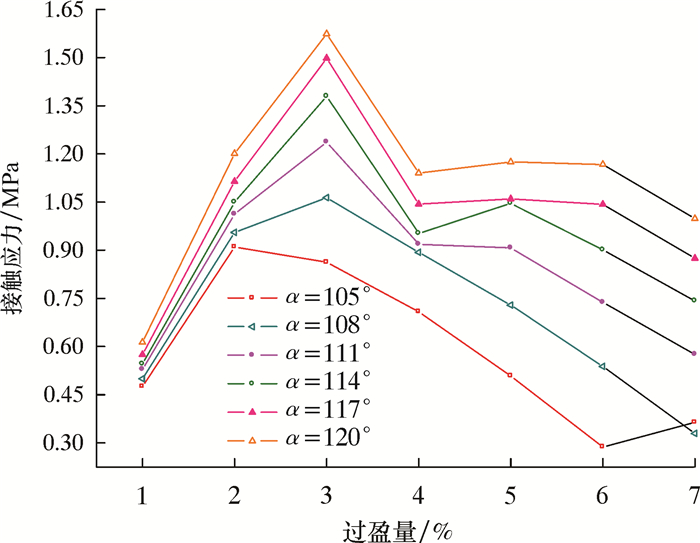
固定皮碗厚度为30 mm,分析不同弯曲角度的皮碗在过盈量为1%~7%时的接触应力,结果如图 5所示。
|
| 图 5 不同过盈量时的最大接触应力 Fig.5 The maximum contact stress under different interferences |
从图 5可以看出:当过盈量相同时,唇部弯曲角度越大,皮碗与管壁的接触应力越大;除弯曲角度为105°的皮碗外,其余各皮碗的接触应力变化趋势基本一致,均呈现出随过盈量的增大,接触应力先增后减的现象;在过盈量为3%时,接触应力达到最大值,说明过盈量在1%~3%范围内,皮碗压缩量对接触应力的大小起主导作用;当过盈量超过3%时,接触应力逐渐减小,说明在这个阶段内,皮碗与管壁的接触面积迅速增大,压缩量对接触应力的作用小于接触面积的作用。对于弯曲角度为105°的皮碗,2%的过盈量即为压缩量与接触面积作用大小的临界点,当过盈量在6%~7%范围内,接触应力有小幅增大。其原因可能是皮碗唇部弯曲角度较小,过盈量较大,使得碟形皮碗与管壁的接触近似于直板皮碗与管壁接触,其接触应力随过盈量的增大而增大。
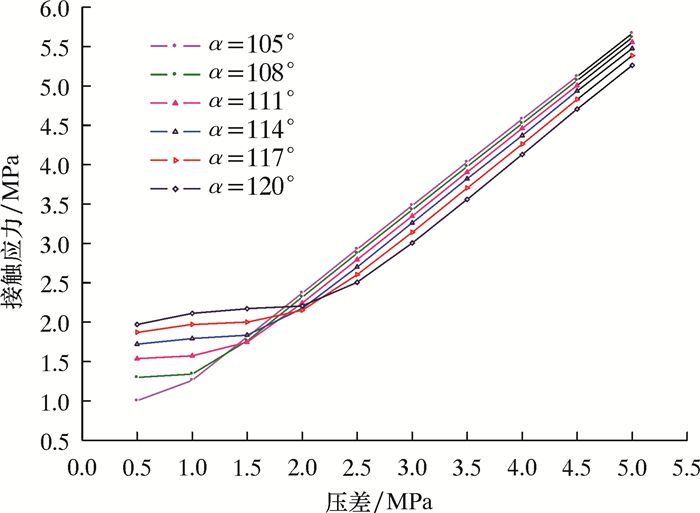
3.2 不同压差时接触应力分析固定皮碗厚度为30 mm,过盈量为4%,压差设置为0.5~5.0 MPa,间隔0.5 MPa,分析压差对皮碗接触应力的影响,结果如图 6所示。
|
| 图 6 不同压差时最大接触应力 Fig.6 The maximum contact stress under different pressure differentials |
从图 6可见:皮碗与管壁的接触应力均随压差的增大而增大,这是因为当压差增大时,作用在皮碗上的挤压力增大,进而导致接触应力增大,这与之前的理论分析一致;唇部弯曲角度越大,皮碗与管壁的接触应力增幅越小,说明压差在皮碗唇部产生的力的一部分会使皮碗唇部弯曲变形,而唇部弯曲角度越大,使皮碗唇部弯曲变形的力就越大,进而导致皮碗与管壁的接触应力减小;当压差在0.5~1.5 MPa的范围内时,在相同压差作用下,唇部弯曲角度越大,接触应力也越大,说明在此阶段接触面积对接触应力的影响占主导地位,唇部弯曲角度越大,皮碗与管壁的接触面积越小,从而导致相同压差下,接触应力越大。
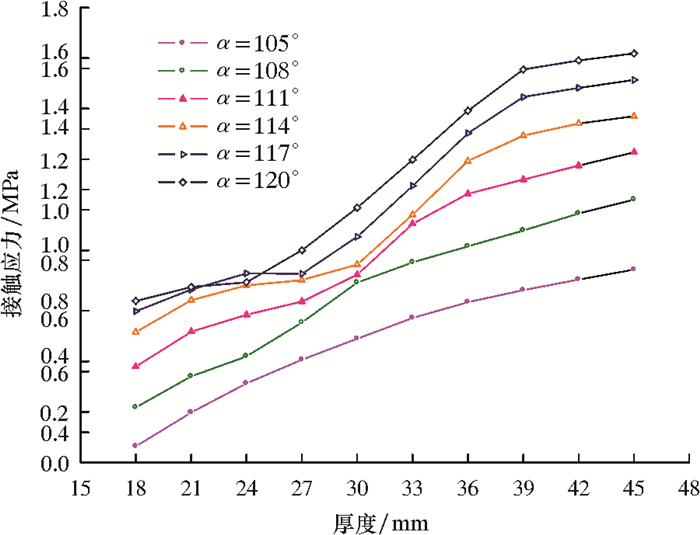
3.3 不同厚度时接触应力分析固定皮碗过盈量为4%,皮碗厚度设置为18~45 mm,间隔3 mm,分析皮碗厚度对接触应力的影响,结果如图 7所示。
|
| 图 7 不同厚度时的最大接触应力 Fig.7 The maximum contact stress under different thicknesses |
从图 7可见:各弯曲角度的皮碗与管壁的接触应力均随皮碗厚度的增大而增大,这是因为随皮碗厚度的增大,皮碗的刚度增大,压缩皮碗变形所需要的力也会增大,进而导致皮碗与管壁的接触应力变大;在相同皮碗厚度下,皮碗唇部弯曲角度越大,接触应力越大;过盈量不变时,接触应力的增幅随唇部弯曲角度的增大而增大,这说明皮碗唇部弯曲角度越大,压缩变形所需要的力越大。
4 结论(1) 通过对皮碗进行定性分析,得出皮碗与管壁间的摩擦阻力与皮碗的厚度、过盈量、所受压差和接触长度有关,通过调整各个结构参数可以优化清管器皮碗受到的摩擦力。
(2) 在相同过盈量下,皮碗唇部弯曲角度越大,皮碗的接触应力越大,当过盈量大于3%时,皮碗接触应力均减小;当压差在0.5~1.5 MPa范围内时,在相同压差作用下,唇部弯曲角度越大,接触应力也越大;在压差逐渐增大时,皮碗的接触应力增幅随唇部弯曲角度的增大而减小;在相同皮碗厚度下,皮碗唇部弯曲角度越大,接触应力越大;当厚度逐渐增大时,接触应力的增幅随唇部弯曲角度的增大而增大。
(3) 当皮碗被用作密封皮碗时,应该重点考虑其密封性,由于不受压差作用,可以只考虑皮碗自身的力学特性。通过研究得到,当皮碗唇部弯曲角度为105°、过盈量为2%~5%、厚度为30 mm时,可以在满足其密封性的基础上产生较小的接触应力;当皮碗用作驱动皮碗时,由于需要承受压差,要求皮碗对压差的敏感度低,皮碗唇部弯曲角度为120°、过盈量为4%、厚度为24~30 mm时,可以在满足驱动功能的基础上产生较小的接触应力。
| [1] |
DAVIDSON R. An introduction to pipeline pigging[C]. Proceedings of the Pigging Products and Services Association Seminar. Aberdeen: [s.n.], 2002.
|
| [2] |
TIRATSOO J. Pipeline pigging and integrity technology[M]. 4th ed. London: Clarion Technical Publishers, 2013.
|
| [3] |
WANG Q, SARICA C, VOLK M. An experimental study on wax removal in pipes with oil flow[J]. Journal of Energy Resources Technology, 2008(130): 11-15. |
| [4] |
BLUNK J A. Composition for paraffin removal from oilfield equipment: 6176243B1[P]. 2001.
|
| [5] |
RONNINGSEN H P. Production of waxy oils on the Norwegian Continental Shelf:experiences, challenges, and practices[J]. Energy & Fuels, 2012, 26(7): 4124-4136. |
| [6] |
中国石油天然气集团公司天然气与管道专业标准化技术委员会.机械清管器技术条件: Q/SY 1262-2010[S].北京: 石油工业出版社, 2010. CNPC Technical Committee for the Professional Standardization of Natural Gas and Pipeline. Mechanical pipeline pig technical specification: Q/SY 1262-2010[S]. Beijing: Petroleum Industry Press, 2010. |
| [7] |
张行, 王焱, 张仕民, 等. 清管器密封皮碗力学特性的有限元分析[J]. 油气储运, 2015, 34(11): 1225-1230. ZHANG H, WANG Y, ZHANG S M, et al. Finite-element analysis on mechanical properties of sealing disc for pig[J]. Oil & Gas Storage and Transportation, 2015, 34(11): 1225-1230. |
| [8] |
陈浩, 刘小明. 清管器皮碗在不同过盈量下的接触应力分析[J]. 管道技术与设备, 2015(6): 43-46. CHEN H, LIU X M. Analysis on contact stress of pig's cup under different interference[J]. Pipeline Technique and Equipment, 2015(6): 43-46. DOI:10.3969/j.issn.1004-9614.2015.06.015 |
| [9] |
秦柏, 邵俊鹏, 张艳芹, 等. 环形橡胶径向刚度特性仿真分析[J]. 哈尔滨理工大学学报, 2009, 14(3): 51-55. QIN B, SHAO J P, ZHANG Y Q, et al. Radial stiffness characteristics simulation analysis of annular rubber[J]. Journal of Harbin University of Science and Technology, 2009, 14(3): 51-55. DOI:10.3969/j.issn.1007-2683.2009.03.013 |
| [10] |
尹素仙.橡胶球铰的刚度与疲劳寿命分析[D].湘潭: 湘潭大学, 2010. YIN S X. Studies on stiffness and fatigue life of rubber bushing[D]. Xiangtan: Xiangtan University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10530-1011028970.htm |
| [11] |
赵存生, 朱石坚. 橡胶金属环静刚度特性研究[J]. 中国机械工程, 2004, 15(11): 962-964. ZHAO C S, ZHU S J. Study on the static stiffness characteristics of rubber-mental ring[J]. China Mechanical Engineering, 2004, 15(11): 962-964. DOI:10.3321/j.issn:1004-132X.2004.11.007 |
| [12] |
石琴, 陈无畏, 洪洋, 等. 基于有限元理论的轮胎刚度特性的仿真研究[J]. 系统仿真学报, 2006, 18(6): 1445-1449. SHI Q, CHEN W W, HONG Y, et al. The simulation of tire's stiffness characteristics using finite element model[J]. Journal of System Simulation, 2006, 18(6): 1445-1449. DOI:10.3969/j.issn.1004-731X.2006.06.009 |
| [13] |
孙伟, 李以农, 刘万里, 等. 橡胶隔振器非线性动态特性建模及实验研究[J]. 振动与冲击, 2012, 31(23): 71-76. SUN W, LI Y N, LIU W L, et al. Dynamic modeling and test for a nonlinear rubber damper[J]. Journal of Vibration and Shock, 2012, 31(23): 71-76. DOI:10.3969/j.issn.1000-3835.2012.23.013 |
| [14] |
高剑虹, 陈佳彬. 管状橡胶支座径向刚度的非线性有限元分析[J]. 山西建筑, 2010, 36(22): 68-69. GAO J H, CHEN J B. On nonlinear finite element analysis of radial stiffness of pipe rubber bearing[J]. Shanxi Architecture, 2010, 36(22): 68-69. DOI:10.3969/j.issn.1009-6825.2010.22.043 |
| [15] |
刘萌, 王青春, 王国权. 橡胶Mooney-Rivlin模型中材料常数的确定[J]. 橡胶工业, 2011, 58(4): 241-245. LIU M, WANG Q C, WANG G Q. Determination for material constants of rubber Mooney-Rivlin model[J]. China Rubber Industry, 2011, 58(4): 241-245. DOI:10.3969/j.issn.1000-890X.2011.04.009 |



