2. 湖北省油气钻完井工具工程技术研究中心;
3. 非常规油气湖北省协同创新中心;
4. 长庆油田分公司油气工艺研究院
2. Oil and Gas Drilling and Well Completion Tools Research Center of Hubei Province;
3. Hubei Cooperative Innovation Center of Unconventional Oil and Gas;
4. Oil & Gas Technology Research Institute of Petro China Changqing Oilfield Company
0 引言
目前,随着非常规油气田的开发,水平井和大位移井等钻井技术不断发展并被广泛应用,但技术发展的同时,管柱下入难问题日益突出。管柱在下入过程中,通过造斜段和水平段时会与井筒接触产生摩擦阻力,同时在整个井筒中,管柱受黏滞阻力和流体摩阻力的影响。若下入管柱的轴向分力大于其产生的综合摩阻力,即管柱能产生一个向下的轴向作用力,则认为管柱可以下入。其中钩载为轴向作用力的平衡力,因此管柱下入能力主要取决于摩阻和钩载。
针对下入管柱载荷的研究,国外学者最先开始建立了“软杆”和“刚杆”模型来研究油管在井眼中的受力情况[1-2]。随后C.A.JOHANCSIK提出了软索模型[3]。文献[4]在扭矩损失的计算中引入转动摩擦因数,在Johancsik模型的基础上进行了完善。文献[5]建立了能够用于对轴向拉力和扭矩分析的平面和空间数学模型。文献[6]利用间隙微元法描述了钻柱与井壁的接触情况。
在国内,许多学者对定向井和水平井中的载荷问题提出了各自的分析方法。文献[7]提出了有限元分析方法,文献[8]提出了有限差分和牛顿迭代法,文献[9]提出了油管力学解析法。目前大部分油田修井作业采用管柱组合两种线重油管的方式来提高管柱下入能力,其原理是通过增大垂直段和造斜段部分组合管柱的重力来增大管柱向下的轴向作用力,但是针对组合管柱的载荷计算问题尚无基础研究。
基于此,结合油田现状,笔者充分考虑井眼轨迹、环空流体摩阻力、流体黏滞阻力、组合管柱在各井段受力特点以及井眼尺寸等因素的影响,建立了组合管柱在修井作业下入过程中与流体相互作用情况下在水平井垂直段、造斜段及水平段的载荷计算模型。相比于其他水平井管柱的载荷计算模型,该模型更加符合水垂比较高,水平段较长的组合管柱修井工况。利用该模型,通过软件求解对现场实际井况进行了计算分析。分析结果表明,该模型计算精度较高,可为现场实践应用提供技术参考。
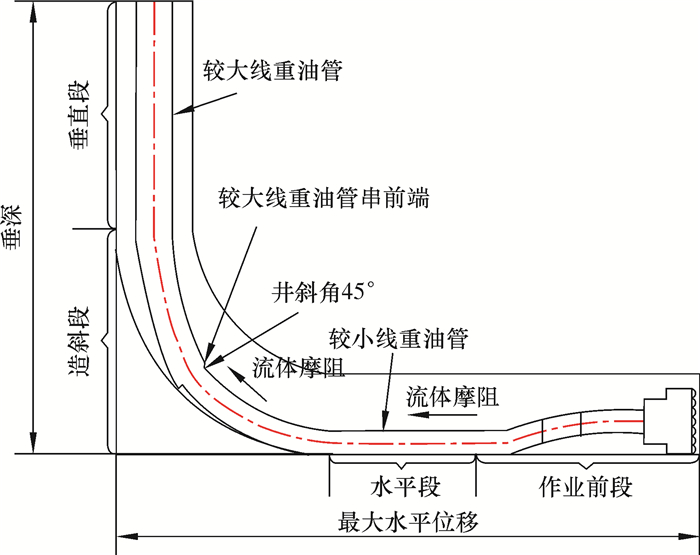
1 计算模型的建立选取水平井从井口到井底整个部分为研究对象,将组合管柱沿井眼轴向阶段划分为垂直段、造斜段、水平段和作业前端四段(见图 1),井筒中的组合管柱主要由前端修井工具串连接两种线重油管组合,由于受到井眼轨迹、黏滞阻力、环空流体摩阻力和流体相互作用机理等因素的影响,不同井段管柱受力方式和受力情况不同[10]。因此,研究不同井段管柱受力方式和受力情况,是计算管柱下入载荷最根本的部分。其中作业前端是指组合管柱前段的修井工具串,并分螺杆前、后段两部分考虑。把两个井眼轨迹测点之间的部分看作是一个连续微元段,则垂直段、造斜段及水平段管柱可以离散成n-1个微元段。
|
| 图 1 组合管柱结构 Fig.1 Structure of the combined string |
在建模之前做如下基本假设:①工具串的长度远小于管柱的长度,因此工具串后端水平段油管视为与井筒连续性接触;②管柱的轴线与井眼轨迹的轴线一致;③磨鞋工具直径最大,比后端管柱先与井筒接触,因此工具串前端可以简化成悬臂梁模型;④管柱在各井段与井筒的接触摩擦因数取平均值。采用摩擦因数拟合法计算出摩擦因数为0.3。
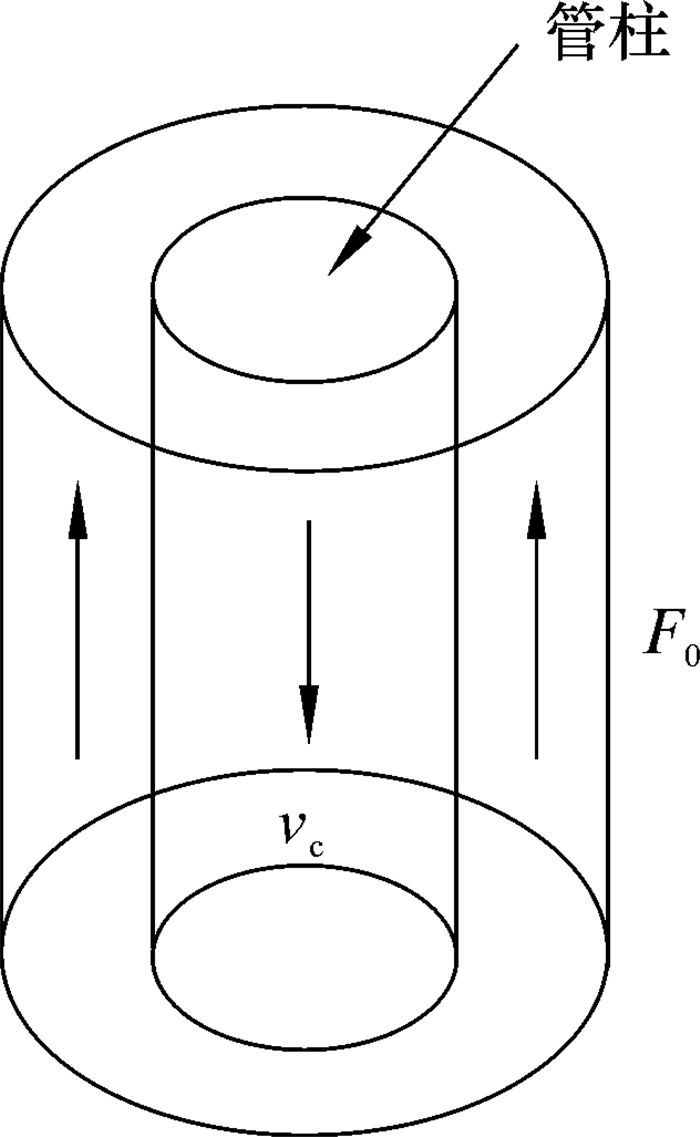
1.1 综合流体摩阻力在实际修井作业中,当组合管柱下入或循环修井液时,管柱与环空流体存在相对运动[11],在管壁必将产生环空流体摩阻力F0,如图 2所示。同时由流体黏性引起的黏滞阻力为Fb,其管柱微元段的综合流体摩阻力Fi为:
|
| 图 2 管柱受环空流体摩阻 Fig.2 The fluid friction of string subjected to annulus flow |
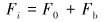
|
(1) |
直井段环空流体摩阻力为:
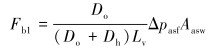
|
(2) |
造斜段和水平段环空流体摩阻力为:
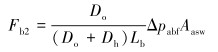
|
(3) |
管柱变径处流体摩阻力为:
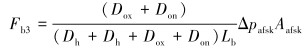
|
(4) |
其中:
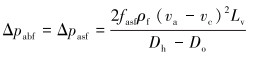
|
(5) |
黏滞阻力为:
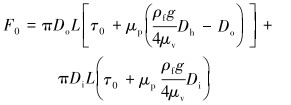
|
(6) |
式中:Do为管柱外径,m;Di为管柱内径,m;Dh为井筒内径,m;L为管柱下入深度,m;τ0为流体动切力,Pa;μp为流体黏度,mPa·s;μv为流体表观黏度,Pa·s;Δpasf为直井段内流体压降MPa;Δpabf为造斜段和水平段内流体压降,MPa;Lv为管柱直井段下入深度,m;ρf为流体密度,kg/m3;vc为管柱下入速度,m/s;va为环空流体速度,m/s;Aasw为环空面积,m2;Lb为管柱造斜段或水平段下入深度,m;Dox为大管柱外径,m;Don为小管柱外径;Δpafsk为环空缩扩结构压降,MPa;Aafsk为变径环空面积;fasf为流体摩阻系数。
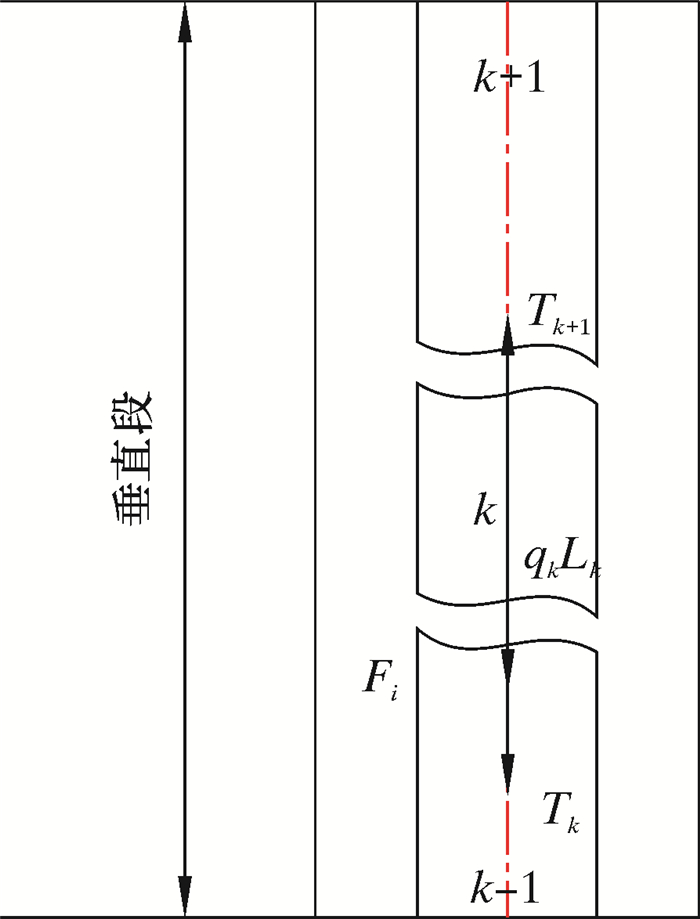
1.2 垂直井段管柱受力分析在垂直段,组合管柱与井筒接触较少,因此可以不考虑井筒对管柱的力学影响,只需要考虑管柱自重、环空流体摩阻力及黏滞阻力。取垂直井段的管柱微元段进行受力分析,如图 3所示。
|
| 图 3 垂直井段的管柱受力 Fig.3 The force on the string in the vertical section |
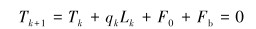
|
(7) |
式中:Nk为考虑浮力后的井筒对管柱的支撑力,N;Tk+1、Tk分别为管柱微元段上、下面所受到的轴向力,N;qk为管柱在流体中的线重,N/m;Lk为管柱微元段长度,m。
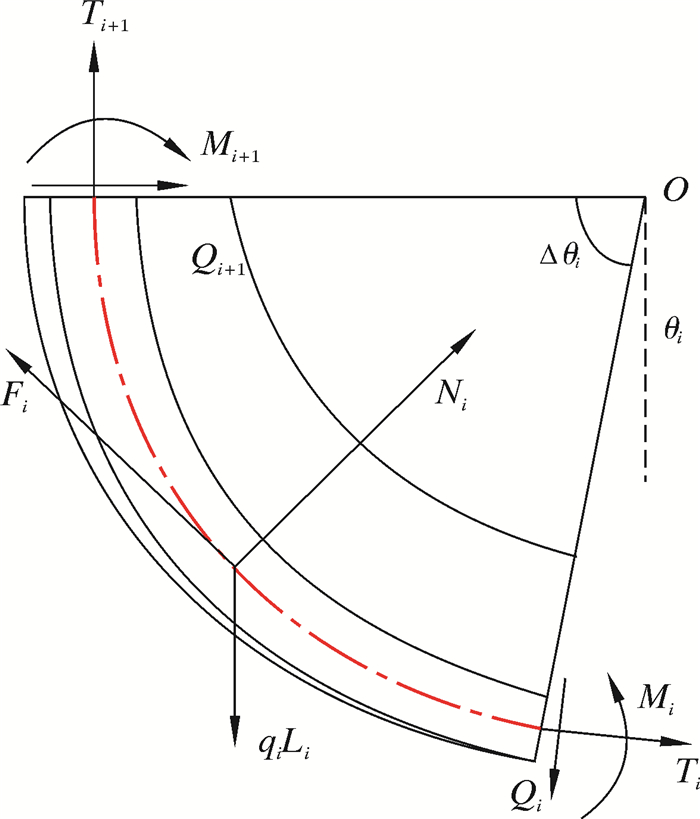
1.3 造斜井段的管柱受力分析当组合管柱到达造斜段时,由于井眼轨迹的弯曲,井筒为刚性,假设造斜段井眼轨迹中心轴线为一铅垂平面上的曲线。同时,管柱与井筒大面积接触,使得管柱受到较大的摩阻力。随着井眼的弯曲,管柱也产生弯曲,从而与直井段的受力特点不一样。基于流体与管柱的相互作用机理,考虑管柱与井筒接触产生的摩阻力和流体对管柱产生的环空流体摩阻力与黏滞阻力,取造斜井段的管柱微元段进行受力分析,如图 4所示。
|
| 图 4 造斜井段的管柱受力 Fig.4 The force on the string in the inclined section |
此时管柱造斜段的力学平衡方程及弯矩平衡方程为:

|
(8) |

|
(9) |
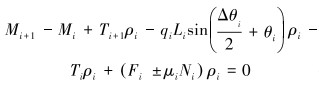
|
(10) |
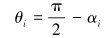
|
(11) |
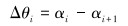
|
(12) |

|
(13) |
式中:Ni为考虑浮力后的井筒对管柱的支撑力,N;Ni≥0时取“+”,Ni<0时取“-”;Ti+1、Ti分别为管柱微元段上、下截面所受到的轴向力,N;qi为管柱在流体中的线重,N/m;Li为管柱微元段长度,m;αi、αi+1为管柱微元段截面上的井斜角,(°);μi为管柱与井筒的接触摩擦因数;Qi、Qi+1为管柱两截面的剪切力,N;Mi、Mi+1为管柱微元段截面上的弯矩,N·m;ρi为弯曲段曲率半径,m。
1.4 作业前端及水平段管柱受力分析基于钻磨工况下,组合管柱作业前端是指管柱前端的修井工具串,分两部分考虑,在螺杆前端考虑管柱做周向转动和轴向运动,与井筒和磨铣物产生摩阻扭矩,为复合运动段;后端管柱考虑做轴向运动,与井筒连续性接触产生摩擦力,为轴向运动段;其中井眼轴线并不水平,井斜角并不一定为90°,如图 5所示。其中磨鞋工具直径最大,比后端管柱先与井筒接触,产生弯曲变形,因此螺杆前端l长度的管柱可以简化为悬臂梁模型。梁的一端固定约束,另一端受后端管柱施加的集中力Fc,如图 6所示。

|
| 图 5 水平段处作业前端管柱受力 Fig.5 The force on the front string at the horizontal section |

|
| 图 6 水平段处作业前端管柱受力模型 Fig.6 The force model on the front string at the horizontal section |
建立挠曲线方程和端面转角方程:
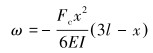
|
(14) |
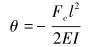
|
(15) |
复合运动段的管柱受力方程如下,轴向运动段管柱的受力与水平段管柱的受力相同,相比较复合运动段管柱忽略扭矩的影响。其中组合管柱前端轴向力的边界条件为井底钻压[12-13]。

|
(16) |

|
(17) |
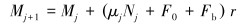
|
(18) |
式中:Mj+1、Mj为管柱截面上的扭矩,N·m;αj为井斜角,(°);r为管柱微元段半径,m;ω为挠度,m;θ为转角,(°);E为弹性模量,Pa;I为管柱截面惯性矩,m4;x为梁的任一横截面;Nj为考虑浮力后的井筒对管柱的支撑力,N;Tj+1、Tj分别为管柱微元段上、下截面所受到的轴向力,N;qj为管柱在流体中的线重,N/m;Lj为管柱微元段长度,m;αj为管柱微元段上的井斜角,(°);μj为管柱与井筒的接触摩擦因数;l为管柱弯曲变形长度,m。
组合管柱在下入修井过程中具有轴向运动与周向转动,根据这两个运动的速度大小比例把螺杆前端管柱的摩擦因数μ利用速度分解法分解为轴向摩擦因数分量μz和切向摩擦因数分量μt[14]。

|
(19) |
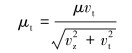
|
(20) |
式中:vz、vt分别为管柱轴向速度和周向速度,m/s。
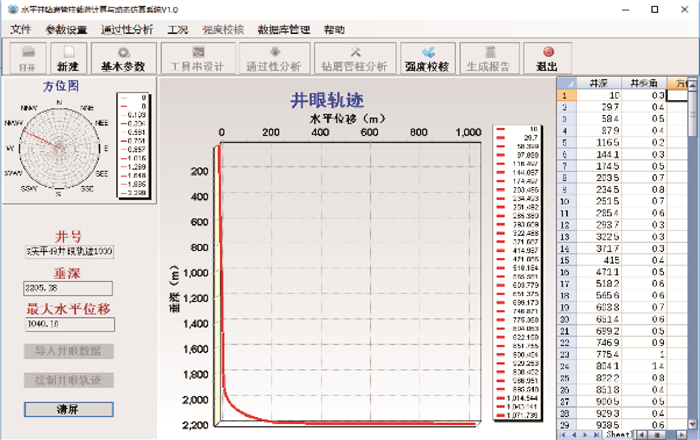
2 模型求解基于C#语言环境,笔者编写了针对修井作业组合管柱在水平井各段下入过程中载荷计算软件,进而分析管柱的下入能力。针对组合管柱的载荷求解,首先在软件参数输入界面对组合管柱的基本参数进行设置,并在管柱组合设计界面中按照管柱下入顺序选择工具并设置其下入深度,最后再对两种线重油管的下入深度进行设置。软件在求解方程时首先对各井段管柱依次判别油管组合,再采用插值法和迭代法对管柱受力模型进行求解计算,其软件求解流程如图 7所示。软件界面输入组合管柱相关参数后载入分析计算,井眼轨迹界面和参数输入界面分别如图 8和图 9所示。

|
| 图 7 软件求解流程 Fig.7 Software solution process |
|
| 图 8 井眼轨迹界面 Fig.8 Well trajectory interface |

|
| 图 9 组合管柱参数输入界面 Fig.9 Parameter input interface of the combined string |
3 应用实例
已知阳平A、安平B、安平C、川平D和川平E水平井井眼轨迹,在钻磨工况下,管柱工具串组合:ø118 mm平底磨鞋×0.23 m+接头×0.16 m+水平井螺杆钻×3.72 m+变径×0.19 m+短节×1.50 m+ø73.0 mm油管。修井参数为:钻压12 MPa,井口压力4 MPa,工作泵压8 MPa,修井液排量700 L/min,修井液密度1 000 kg/m3,螺杆功率40 kW,额定扭矩1 490 N·m。
软件计算结果如表 1所示。钩载与现场数据对比的最大误差为11.7%,平均误差为7.25%;摩阻的最大误差为14.7%,平均误差为9.5%。这说明模型误差较小,完全满足工程需要。
| 井号 | 井深/m | 实际钩载/kN | 实际摩阻/kN | 模拟钩载/kN | 模拟摩阻/kN |
| 阳平A | 3 725 | 160.0 | 20.4 | 144.6 | 23.4 |
| 安平B | 3 198 | 180.0 | 24.5 | 155.6 | 24.7 |
| 安平C | 3 027 | 162.0 | 20.3 | 159.0 | 21.5 |
| 川平D | 3 123 | 160.0 | 15.2 | 172.0 | 13.1 |
| 川平E | 3 189 | 152.0 | 16.3 | 167.0 | 14.3 |
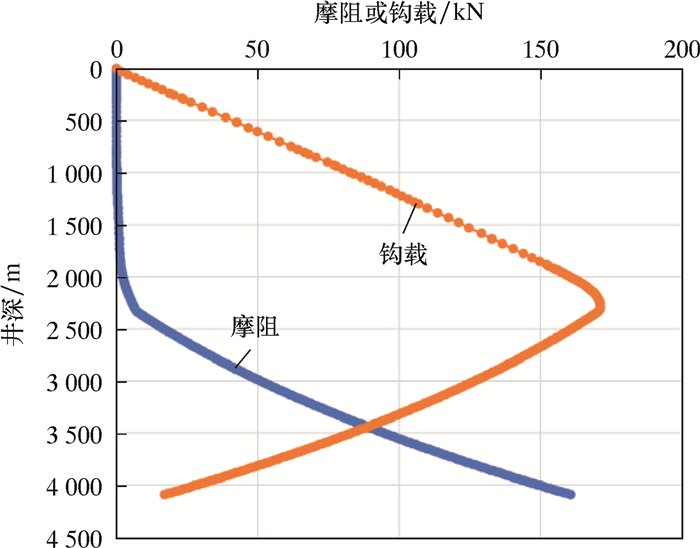
以庆平F水平井为例,朝一个方向延长水平段距离,增大水垂比,井深为4 090.00 m,垂深为2 211.97 m,最大水平位移为2 030.36 m。选取与上述相同的工具串和修井参数,其中管柱采用组合单一ø73.0 mm油管。如图 10所示,管柱达到井底时钩载为17.2 kN,摩阻为160.5 kN。
|
| 图 10 ø73.0 mm油管管柱的摩阻或钩载 Fig.10 Drag/hook load of the ø73.07 mm tubing string |
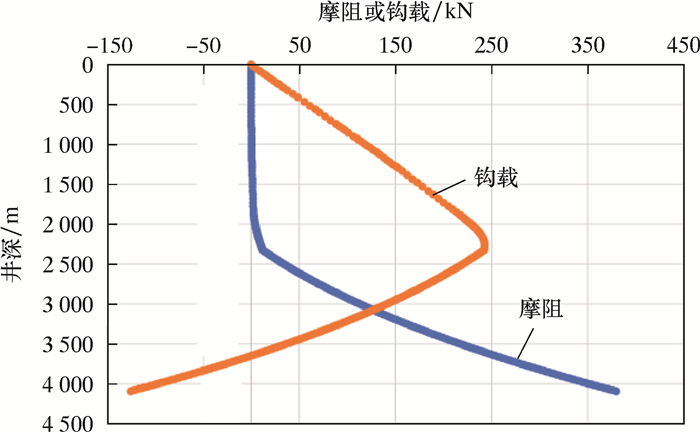
管柱改用组合单一ø88.9 mm油管,结果如图 11所示。由图 11可知,管柱下到井深3 648.65 m处,钩载为0.074 kN,此时管柱无法下入。
|
| 图 11 ø88.9 mm油管管柱的摩阻或钩载 Fig.11 Drag/hook load of the ø88.9 mm tubing string |
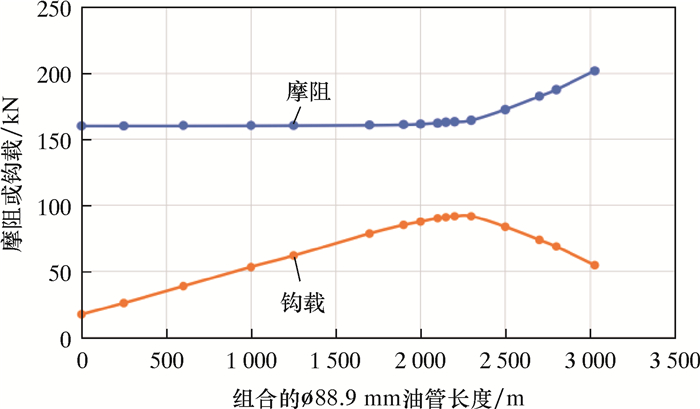
管柱改用组合ø73.0和ø88.9 mm两种线重组合油管,摩阻和钩载计算结果如图 12所示。由图 12可知:两种线重油管不同比例的组合管柱可以下入到井底,当整个管柱长度不变时,随着ø88.9 mm油管所占长度增大,整个管柱下入到井底位置时的摩阻和钩载相应增大;当ø88.9 mm油管的比例长度可以下入到造斜段井深一定值时,摩阻的增长率开始增大,钩载减小,此时发现随ø88.9 mm油管所占长度的增加对组合管柱的下入产生了阻碍,因此管柱最优组合比例的临界条件在造斜段。
|
| 图 12 ø88.9 mm油管占比长度变化的摩阻或钩载 Fig.12 Drag/hook load of the ø88.9 mm tubing string under different tubing length ratio |
针对组合管柱中ø88.9 mm油管下入到造斜段不同井斜角深度时进行模拟分析,结果如图 13所示。由图 13可知,当ø88.9 mm油管所占长度可以下入到井斜角45°左右井深时,组合管柱下入到井底时的钩载最大,此时管柱组合比例最优,管柱具有最强的下入能力。

|
| 图 13 ø88.9 mm油管前端下入到造斜段不同位置的井底钩载 Fig.13 The hook load with the ø88.9 mm front tubing string run into different depths of the inclined section |
为了研究ø88.9 mm油管下入深度位于井斜角45°左右的井深时,最优比例组合管柱与单一油管管柱相比它的下入能力是否最强,利用载荷计算软件进行了模拟计算,计算结果如图 14所示。由图 14可以看出,当管柱下入到井底时,钩载为88.1 kN,摩阻为166.7 kN。

|
| 图 14 ø73.0 mm油管管柱最大下入深度 Fig.14 Maximum running depth of the ø73.0 mm tubing string |
由上述分析可知,采用组合管柱下入作业,其中ø88.9 mm油管前端下入到井斜角45°左右井深时,相较于单一油管管柱,虽然下入到井底时摩阻有所增加,但钩载增加较大,下入能力最强。
4 结论(1) 充分考虑井眼轨迹、环空流体摩阻、流体黏滞力、管柱在各井段受力特点以及井眼尺寸等因素的影响,分析了组合管柱与井筒内壁之间的摩阻和钩载与管柱下入能力之间的关系,将水平井分为4段,建立了组合管柱在水平井各段下入过程中与流体相互作用情况下载荷的计算模型。
(2) 运用插值法和迭代法开发了相应软件,实现了水平井修井作业组合管柱的载荷模型求解;对比软件计算结果与实测数据,钩载和摩阻的平均误差分别为7.25%和9.5%,这说明模型具有较高的准确性。
(3) 通过计算组合管柱与单一油管管柱的摩阻和钩载,发现组合管柱中线重较大油管下入到井斜角45°左右的井深时,管柱组合比例最优,相较于单一油管管柱和不同比例管柱组合,此时管柱下入能力最强。
| [1] |
刘格宏.水平井多级压裂管柱力学分析及软件开发[D].成都: 西南石油大学, 2017. LIU G H. Mechanical analysis and software development of multistage fracturing string in horizontal well[D]. Chengdu: Southwest Petroleum University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10615-1017256592.htm |
| [2] |
刘修善. 井眼轨迹的平均井眼曲率计算[J]. 石油钻采工艺, 2005, 27(5): 11-15. LIU X S. Average borehole curvature calculation of hole trajectory[J]. Oil Drilling & Production Technology, 2005, 27(5): 11-15. DOI:10.3969/j.issn.1000-7393.2005.05.003 |
| [3] |
GAO G H. Effects of boundary conditions and friction on static buckling of pipe in a horizontal well[R]. SPE 111511, 2008.
|
| [4] |
MIRHAJ A, KAARSTAD E, AADNOY B S. Minimizing friction in shallow horizontal wells[R].SPE 135812, 2010.
|
| [5] |
CARPENTER C. Friction-load redistribution for exten-ded-reach and horizontal-well completions[J]. Journal of Petroleum Technology, 2016, 68(11): 65-66. DOI:10.2118/1116-0065-JPT |
| [6] |
MCSPADDEN A R, TREVISAN R. Friction load redi-stribution for robust and cost efficient design of extended reach and horizontal well completions[R].SPE 178905, 2016.
|
| [7] |
郭凤超, 陶亮, 贾晓斌. 水平井钻井管柱力学模型与软件开发[J]. 石油机械, 2013, 41(7): 28-32. GUO F C, TAO L, JIA X B. Mechanical model of horizontal drilling string and software development[J]. China Petroleum Machinery, 2013, 41(7): 28-32. DOI:10.3969/j.issn.1001-4578.2013.07.008 |
| [8] |
刘朕, 练章华, 王磊, 等. 定向井全井段钻柱下放过程应力及接触力分析[J]. 石油机械, 2012, 40(6): 13-16. LIU Z, LIAN Z H, WANG L, et al. Stress and contact force analysis of whole hole drill sting rungning in directional well[J]. China Petroleum Machinery, 2012, 40(6): 13-16. |
| [9] |
张杨.水平井套管摩阻计算与可下入性分析[D].成都: 西南石油大学, 2015. ZHANG Y. Calculation and analysis of casing friction in horizontal well[D]. Chengdu: Southwest Petroleum University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10615-1015599074.htm |
| [10] |
冯定, 施雷, 夏成宇, 等. 定向井的多层分注管柱串通过性分析[J]. 西南石油大学学报(自然科学版), 2016, 38(3): 162-169. FENG D, SHI L, XAI C Y, et al. The pass-through capacity analysis for multi-layer injectionstrings in directional wells[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2016, 38(3): 162-169. |
| [11] |
冯定, 鄢标, 夏成宇, 等. 井眼轨迹控制工具主轴力学行为分析[J]. 科学技术与工程, 2016, 16(4): 173-177. FENG D, YAN B, XIA C Y, et al. The mechanical behavior analyse of spindle in wellboretrack control tool[J]. Science Technology and Engineering, 2016, 16(4): 173-177. DOI:10.3969/j.issn.1671-1815.2016.04.032 |
| [12] |
陈勇, 蒋祖军, 练章华, 等. 水平井钻井摩阻影响因素分析及减摩技术[J]. 石油机械, 2013, 41(9): 29-32. CHEN Y, JIANG Z J, LIAN Z H, et al. Analysis of influencing factors of horizontal drilling friction and antifriction technology[J]. China Petroleum Machinery, 2013, 41(9): 29-32. DOI:10.3969/j.issn.1001-4578.2013.09.007 |
| [13] |
孙巧雷, 冯定, 杨行, 等. 轴向载荷波动下海上测试管柱动力响应与安全系数分析[J]. 中国安全生产科学技术, 2018, 14(11): 19-25. SUN Q L, FENG D, YANG H, et al. Analysison dynamic response and safety coefficient of offshore testing string under axial load fluctuation[J]. Journal of Safety and Technology, 2018, 14(11): 19-25. |
| [14] |
祝效华, 李柯, 安家伟. 水平井钻柱动态摩阻扭矩计算与分析[J]. 天然气工业, 2018, 38(8): 75-82. ZHU X H, LI K, AN J W. Calculation and analysis of dynamic drag and torque of horizontal well strings[J]. Natural Gas Industry, 2018, 38(8): 75-82. |



