0 引言
近年来,随着辽河油田勘探开发进入中后期,对浅井的开发已不能满足生产需求,对深井和超深井的开发已迫在眉睫。然而辽河油田深部地层的岩石较硬,耐磨极值较高,在深井和超深井钻井作业中,由于地层岩石抗压强度和抗剪强度较大,从而导致PDC钻头急剧磨损,容易发生断裂事故,造成PDC钻头失效。旋冲工具能为PDC钻头提供一个周向上的高频振动切削力,在轴向上提供一个高频脉冲冲击力,这样就可以很好地解决钻柱黏滑和钻头磨损的难题。
目前,国内已经尝试了很多种旋冲工具的研发和现场应用,其工作原理都是由钻井液通过装置内的过流流道驱动动力机构来使锤座产生周向高频冲击力。由于旋冲工具流道结构复杂,高速高压钻井液流经旋冲工具工作元件时,对工作元件冲蚀磨损十分严重,影响着工作元件寿命,严重制约了旋冲工具的推广应用。为此,笔者通过CAD三维建模软件对工具内部典型流道进行建模,并通过FLUENT软件分析旋冲工具内部典型流道不同直径和不同角度工艺孔对液流压力和速度的影响。所得结果可为旋冲工具工作元件的优化设计及寿命延长提供参考。
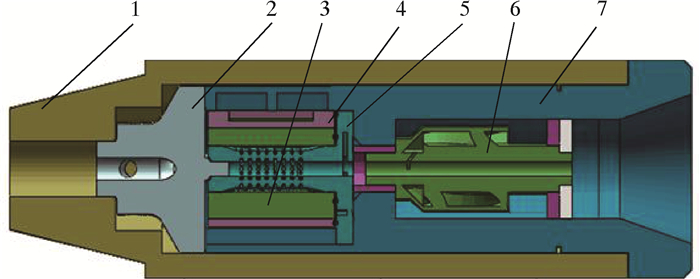
1 旋冲工具工作元件磨损形式探讨旋冲工具由悬挂外筒和悬挂内筒组成,结构如图 1所示。悬挂内筒包括上分流压盖、液动扭转冲击发生器和液力脉冲发生器。液动扭转冲击发生器由内分流座、启动换向器、液动主锤和液动副锤组成,其作用是提供高频的周向冲击扭矩。然而上分流压盖、内分流座以及启动换向器、液动主锤和液动副锤之间的流道都易受到高速高压钻井液的冲刷而磨损,故探讨旋冲工具工作元件的磨损机制对延长工具的寿命具有重要意义。
|
| 1—悬挂外筒;2—上分流压盖;3—启动换向器;4—液动冲击锤;5—内分流座;6—液动旋流器;7—悬挂内筒。 图 1 旋冲工具结构示意图 Fig.1 Structural schematic of the rotary impact tool |
通过对寿命较短的旋冲工具拆卸发现,旋冲工具的上分流压盖和内分流座工艺孔入口处冲蚀磨损较为严重,启动换向器和液动主副锤的工艺孔入口处冲蚀磨损次之。现以内分流座冲蚀磨损(见图 2)为例加以说明。

|
| 图 2 旋冲工具工作元件磨损图 Fig.2 Working element wear diagram of the rotary impact tool |
从内分流座工艺孔入口处磨损表现形式看,造成这一现象的原因是:高压钻井液携带固体颗粒在旋冲工具内各流体通道高速流动,对工作元件的内部结构产生高速磨损,从而使元件的部分结构因冲蚀磨损严重而失效。就外部表现形式看,钻井液对旋冲工具工作元件的磨损与空蚀和化学腐蚀对元件的破坏不一样。空蚀使元件表面材料形成不连续的深细小孔或洞隙,洞隙周围的金属完好无损。化学腐蚀使元件材料浅层剥落,破坏痕迹呈大面积均匀出现。钻井液磨粒磨损使元件材料破坏层相对较深,表面磨损痕迹不均匀、连续有方向性且局部出现[1-2]。
2 钻井液对旋冲工具工作元件磨损的影响在石油钻井中,由于钻井液具有密度大、黏度高、压力高、流速高以及含砂量高等特点,分析钻井液在旋冲工具工作元件内的速度和压力,得到钻井液速度和压力最优下的流道结构参数,对延长元件寿命具有重要意义。下面应用ANSYS软件中的FLUENT模块分析流道结构参数不同时,钻井液速度和压力对旋冲工具工作元件磨损的影响。
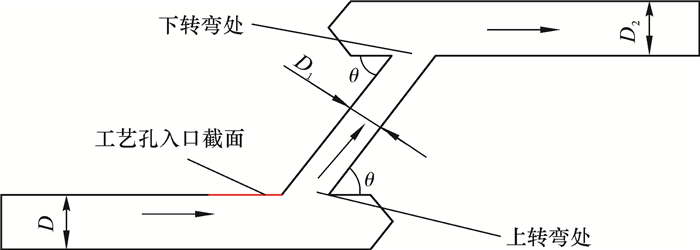
2.1 旋冲工具工作元件典型流道物理模型建立笔者采用典型“Z”形结构流道,包括进液流道、工艺孔流道和出液流道,如图 3所示。冲击器内部流体为不可压缩的黏性流体,流体密度ρ=1 150 kg/m3,动力黏度μ=0.075 kg/(m·s)。根据工况定义边界条件,设定进口速度v=20 m/s,出口压力p=0 Pa,并假定进液口液流为充分发展流,垂直于进液口液流方向上的速度为0,对所有液流流道壁面上都施加无滑移边界条件。D为进液流道直径,D1为工艺孔流道直径,D2为出液流道直径,θ为进液流道与工艺孔流道之间的夹角。
|
| 图 3 典型“Z”形结构流道示意图 Fig.3 Schematic diagram of a typical "Z" shaped flow path |
考虑到流道内会产生湍流漩涡,故选用标准壁面函数,标准的k-ε湍流模型。根据边界条件,采用二阶精度的迎风格式对参数进行离散,应用压力耦合的半隐式方法(SIMPLE)求解该封闭的离散方程组[3-5]。
2.2 数值模拟笔者采用ANSYS软件中的FLUENT模块对旋冲工具内部带工艺孔的流道流场进行数值模拟,采用Tet/Hybird对流道进行混合网格划分[6-10]。设定进液流道和出液流道长度相等,直径D=D2=20 mm,工艺孔直径D1=xD(x=0.25、0.50、0.75和1.00),工艺孔角度θ=15°、30°、45°、60°、75°、90°且θ≤90°。典型“Z”形结构工艺孔入口处模拟结果如表 1所示。
| θ/(°) | 15 | 30 | 45 | 60 | 75 | 90 | |
| D1=0.25D | p/Pa | 120 800 | 121 100 | 118 700 | 79 350 | 77 120 | 122 000 |
| v/(m·s-1) | 394.50 | 408.90 | 401.00 | 382.70 | 367.7 | 410.40 | |
| D1=0.50D | p/Pa | 6 122 | 5 764 | 4 652 | 3 790 | 6 514 | 32 870 |
| v/(m·s-1) | 97.05 | 96.59 | 95.18 | 92.54 | 94.14 | 102.50 | |
| D1=0.75D | p/Pa | 903 | 739 | 620 | 584 | 671 | 1 172 |
| v/(m·s-1) | 44.67 | 43.43 | 42.96 | 41.71 | 43.89 | 49.04 | |
| D1=1.00D | p/Pa | 334 | 275 | 331 | 389 | 425 | 711 |
| v/(m·s-1) | 23.40 | 21.01 | 23.66 | 26.43 | 29.69 | 34.09 | |
3 仿真结果与分析 3.1 不同直径、不同角度工艺孔压力分析
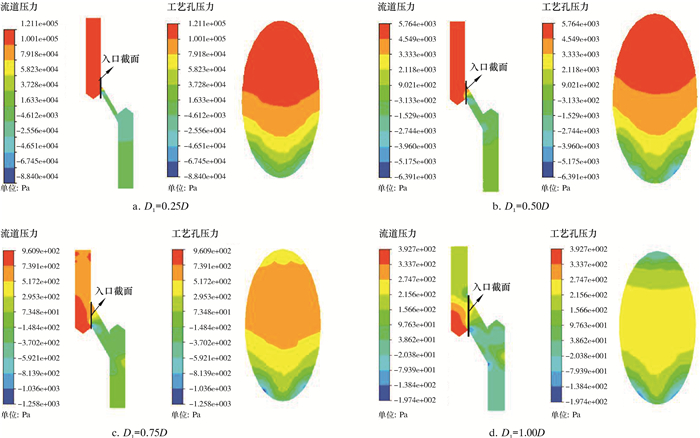
将旋冲工具的工艺孔直径设为D1=xD(x=0.25、0.50、0.75和1.00),工艺孔角度θ=15°、30°、45°、60°、75°和90°。下面针对工艺孔角度θ=30°,不同直径工艺孔的压力云图进行分析,结果如图 4所示。
|
| 图 4 θ=30°时不同工艺孔直径下的压力云图 Fig.4 Pressure distribution at different process hole diameters at θ = 30° |
从压力云图可以发现,在工艺孔角度一定时,随着工艺孔直径的不断增大,进液流道的压力在不断减小,工艺孔入口处压力也在不断减小,并且工艺孔入口处最大压力也从工艺孔上边缘区逐渐移动到工艺孔中心区,从而减小了旋冲工具工作元件受到的压力,减轻了工作元件磨损。当工艺孔直径等于进液流道直径的¼时(见图 4a),进液流道受到的压力是121 100 Pa,工艺孔入口处受到压力也是121 100 Pa。当工艺孔流道直径等于进液流道直径时(见图 4d),进液流道受到的压力是392.7 Pa,工艺孔入口处受到的压力是274.7 Pa。图 4a中工艺孔直径为图 4d中工艺孔直径的¼,而进液流道压力和工艺孔入口处受到的压力是图 4d中进液流道压力和工艺孔入口处压力的308倍和441倍。从流道压力数值模拟发现,在工艺孔直径发生变化时,通过工艺孔流道内的压力会发生巨大变化,并且工艺孔直径等于进液流道直径时最小。
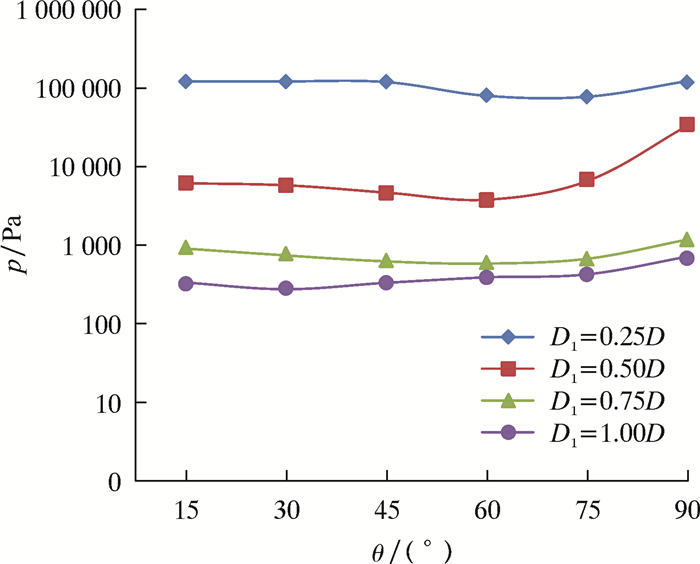
图 5为工艺孔入口压力随θ和工艺孔直径的变化曲线。
|
| 图 5 工艺孔入口压力随θ和D1的变化曲线 Fig.5 Effect of θ and D1 on the process hole inlet pressure |
由图 5可知,在同一个工艺孔角度下,工艺孔入口处压力随工艺孔直径增大而减小,并且在工艺孔直径等于进液孔直径时最小。在同一个工艺孔直径下,随工艺孔角度θ增大工艺孔入口处压力先减小再增大:D1=0.25D时,工艺孔入口处压力最小时的角度是75°;D1=0.50D时,工艺孔入口处压力最小时的角度是60°;D1=0.75D时,工艺孔入口处压力最小时的角度是60°;D1=D时,工艺孔入口处压力最小时的角度是30°。由以上分析发现,当工艺孔直径等于进液孔直径,工艺孔角度等于30°时,进液孔和工艺孔受到的液体压力最小,对工作元件的磨损也最轻。
3.2 不同直径、不同角度工艺孔速度分析取工艺孔角度等于30°,以不同直径工艺孔下的速度云图为对象来分析速度分布规律,结果如图 6所示。
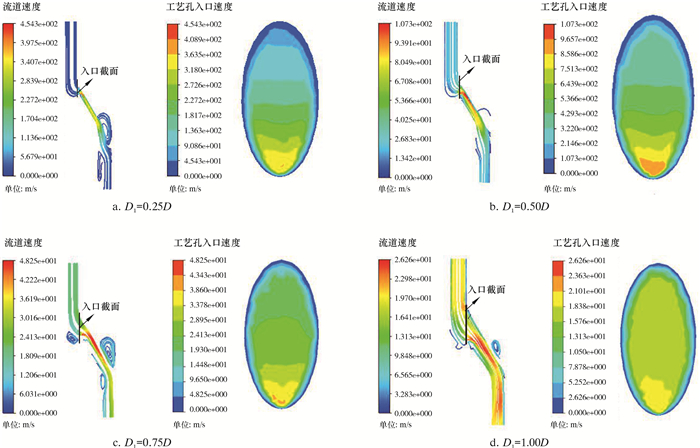
|
| 图 6 θ=30°时不同工艺孔直径下的速度云图 Fig.6 Velocity distribution at different process hole diameters at θ = 30° |
由流道速度数值模拟发现,工艺孔角度一定时,流道模型的最大速度和工艺孔入口处的最大速度随着工艺孔直径的增大而在不断减小,并且在工艺孔直径等于进液流道直径时速度最小,接近数值模拟时设置的流道入口速度。从速度云图可知,在工艺孔入口下方和出口的上方都出现了涡流,并且随着工艺孔直径的增大,涡流能量和大小都在减小,由于钻井液携带着砂石和岩粉,高速涡流会像高速旋转的砂轮对旋冲工具工作元件进行磨损,故流道速度越小,对工作元件的磨损越小;当工艺孔流道直径D1=0.25D时,流道模型的最大速度为454.3 m/s,工艺孔入口处流速是408.9 m/s。当工艺孔流道直径D1=D时,流道模型的最大速度为26.3 m/s,工艺孔入口处流速是21.0 m/s。由此可见,工艺孔流道直径D1=0.25D时,流道模型的最大速度和工艺孔入口处流速是工艺孔流道直径D1=D时的17.3倍和19.5倍,故工艺孔直径对流道流速的影响较大,最佳的工艺孔直径是旋冲工具工作元件较轻磨损的关键。
工艺孔入口速度随θ和工艺孔直径的变化曲线如图 7所示。由图 7可知:在工艺孔直径一定时,工艺孔入口处的速度随工艺孔角度的增大先减小后增大;在工艺孔角度一定时,工艺孔入口处的速度随着工艺孔直径的增大而减小,并且在工艺孔直径D1=D时工艺孔入口处的速度最小。当工艺孔直径等于进液流道直径、工艺孔角度等于30°时,工艺孔入口处的速度最小,这对优化工艺孔直径和角度以及对工艺孔入口处采取何种防磨措施有着重要的现实意义。
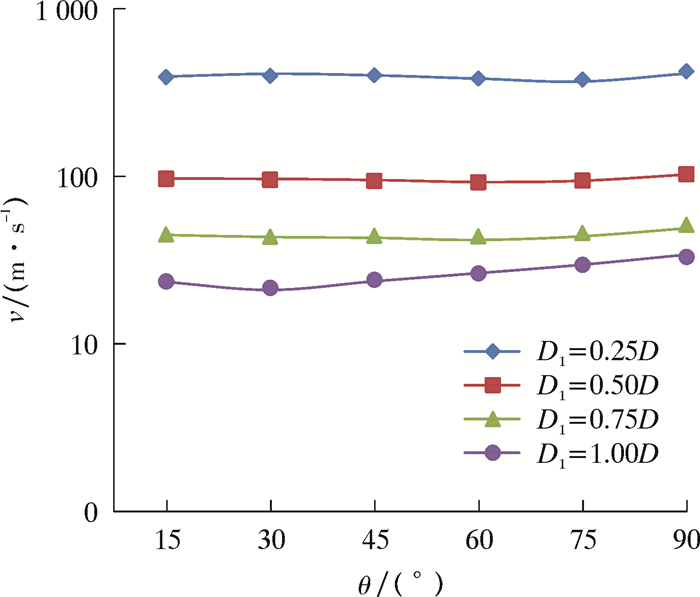
|
| 图 7 工艺孔入口速度随θ和D1的变化曲线 Fig.7 Effect of θ and D1 on the process hole inlet velocity |
4 结论
(1) 通过对旋冲工具工作元件磨损形式进行分析,得到工具工作元件磨损的破坏机理,并确定出钻井液的压力和速度是造成工作元件破坏的关键因素。
(2) 通过对旋冲工具工作元件内部流道进行建模及流场分析,得到工艺孔与进液流道之间的角度和工艺孔直径大小直接影响着流道内钻井液的压力和速度大小。工艺孔与进液流道之间的角度一定时,钻井液在流道内的压力和速度随着工艺孔直径的增大而减小。当工艺孔直径一定时,钻井液在流道内的压力和速度随着工艺孔角度的增大先减小后增大。
(3) 通过分析旋冲工具工作元件磨损机理以及对旋冲工具工作元件内部流场建模,得到最佳的工艺孔直径和工艺孔角度,即工艺孔直径等于进液流道直径、工艺孔角度为30°。这为旋冲工具流道结构优化、性能优化以及防磨措施的制定提供了参考依据。
| [1] |
段国昌. 水轮机砂粒磨损[M]. 北京: 清华大学出版社, 1981. DUAN G C. Turbine sand abrasion[M]. Beijing: Tsinghua University Press, 1981. |
| [2] |
马世兰, 刘建华, 刘天宝, 等. 水力机械泥砂磨损的试验研究[J]. 通用机械, 2005(12): 45-48. MA S L, LIU J H, LIU T B, et al. Hydraulic machinery mud sand abrasion test research[J]. General Machinery, 2005(12): 45-48. DOI:10.3969/j.issn.1671-7139.2005.12.014 |
| [3] |
王福军. 计算流体动力学分析:CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. WANG F J. Computational fluid dynamics analysis:the principle and application of CFD software[M]. Beijing: Tsinghua University Press, 2004. |
| [4] |
EL-SAYED M, SUN T, BERRY J. Shape optimization with computational fluid dynamics[J]. Advances in Engineering Software, 2005, 36(9): 607-613. DOI:10.1016/j.advengsoft.2005.03.009 |
| [5] |
ANAGNOSTOPOULOS J S, MATHIOULAKIS D S. Unsteady flow field in a square tube T-junction[J]. Physics of Fluids, 2004, 16(11): 34-36. |
| [6] |
李广国, 索忠伟, 王甲昌, 等. 射流冲击器配合PDC钻头在超深井中的应用[J]. 石油机械, 2013, 41(4): 31-34. LI G G, SUO Z W, WANG J C, et al. Application of jet hammar and PDC bit in superdeep well[J]. China Petroleum Machinery, 2013, 41(4): 31-34. DOI:10.3969/j.issn.1001-4578.2013.04.008 |
| [7] |
谢天.高频轴向液动冲击器破岩机理及试验分析[D].大庆: 东北石油大学, 2014. XIE T. High frequency axial hydraulic percussive rock fragmentation mechanism and experimental analysis[D]. Daqing: Northeast Petroleum University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10220-1014389632.htm |
| [8] |
蒋宏伟, 黄成, 王克雄, 等. 射吸式液动冲击器内部流场数值模拟研究[J]. 石油机械, 2007, 35(9): 25-28. JIANG H W, HUANG C, WANG K X, et al. Radiation absorption type hydraulic impacter internal flow field numerical simulation research[J]. China Petroleum Machinery, 2007, 35(9): 25-28. DOI:10.3969/j.issn.1001-4578.2007.09.009 |
| [9] |
杜经民, 蔡保全, 李宝仁. 某系统液压集成块流道液流特性分析[J]. 机床与液压, 2010, 38(13): 143-145. DU J M, CAI B Q, LI B R. Analysis for flowing characteristics of fluid inside hydraulic manifold block channels of a certain system[J]. Machine Tool & Hydraulics, 2010, 38(13): 143-145. DOI:10.3969/j.issn.1001-3881.2010.13.043 |
| [10] |
李美求, 曹宇, 王强军, 等. 液动周向扭矩冲击发生器动力学分析[J]. 石油机械, 2015, 43(11): 44-47. LI M Q, CAO Y, WANG Q J, et al. Dynamics of circumferential torque hydraulic shock generator[J]. China Petroleum Machinery, 2015, 43(11): 44-47. |


