0 引言
当外压超过套管所能承受的抗挤强度时,套管会发生挤毁失效,严重时甚至会造成油气田开采作业无法正常进行[1]。钻探过程中,岩性变化和钻压变化会引起井眼弯曲,套管下入水平井弯曲段时,由于井眼构型的影响会发生弯曲变形,进而影响套管的抗外挤强度[2]。目前国内外广泛采用的套管抗挤强度计算公式由API BUL 5C3标准提供[3],但该标准只适用于未发生弯曲变形的套管。为准确评估弯曲变形后套管的抗外挤强度,进而指导现场施工,国内外学者采用解析法、数值模拟和套管强度试验等方法对弯曲段套管的抗挤强度进行了探索研究[4-12]。当井眼曲率增大到一定程度时,套管的弯曲变形由弹性变形过渡到塑性流动,导致弯曲段套管截面扁化。由于扁化问题的复杂性,前期套管抗挤强度研究很少考虑扁化效应的影响,与真实情况相比不可避免存在误差。目前,扁化变形分析多集中于扁化机理及圆管类简单结构,其研究思路可为扁化套管抗挤强度分析提供借鉴。
马更生等[13]应用弹塑性原理,通过有限元软件分析了厚壁钢管截面变形挠度及截面扁化率。ZHANG L.C.等[14]分析了弹性塑料圆管受纯弯曲载荷作用时的扁化情况,推导了圆管弯曲曲率与圆管截面扁化率的关系。鄂大辛等[15-16]分析了弯曲过程中管材的弹塑性变形,推导了最小相对弯曲半径。L.G.BRAZIER[17]采用能量法分析了塑性区内圆柱壳弹性稳定性。钟华勇等[18]通过三点弯曲校直中的截面扁化分析得到锆合金薄壁管类零件扁化率计算公式。T.C.MICHAEL等[19]考察了平面弯曲时薄壁管材的弯矩与截面椭圆率的关系。T.MESHI等[20]以薄壁管材为例,采用有限元法分析了弯曲载荷作用下截面弯矩与变形位移的关系。
目前弯曲段套管抗挤强度分析多未考虑扁化效应的影响,而当井眼曲率增大到一定程度时,套管的弯曲变形由弹性变形过渡到塑性流动,导致弯曲段套管截面扁化,故传统未考虑套管扁化变形进行套管抗外挤强度计算的方法会存在一定的误差。因此,本文借鉴扁化变形在圆管类结构中的研究思路,将其拓展到套管抗挤强度分析,以期得到更切合实际的结论。
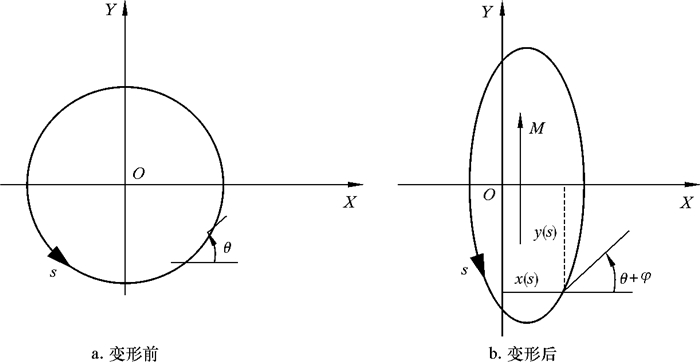
1 外载作用下套管应变分析 1.1 外载作用下套管环向应变分析套管下入水平井弯曲段时,由于井眼构型的影响会发生弯曲变形,在弯矩M及极限外载作用下套管将发生如图 1所示沿X和Y轴对称的均匀扁化变形[21]。
|
| 图 1 套管中间横截面变形示意图 Fig.1 Schematic diagram of the cross-section deformation of the casing |
变形后套管中间横截面微元段弧长ds′=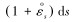
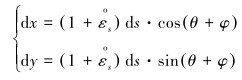
|
(1) |
式中:s为弧长,m;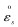
受外压和弯曲联合作用时截面发生变形后,套管截面中线周向曲率半径ρs与套管中间截面微元段弧长关系为[21]:
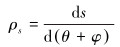
|
(2) |
套管截面变形前与变形后任意周向长度为:
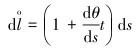
|
(3) |
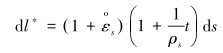
|
(4) |
式中:t为套管壁厚,m;l为变形前套管任意周向长度,m;l*为变形后套管任意周向长度,m。
变形后套管截面任一点的环向应变为:
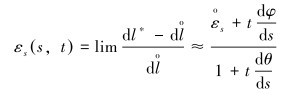
|
(5) |
发生弯曲变形后,凹入侧纵向纤维缩短,凸出侧伸长。考虑到变形的连续性,套管截面中性层线应变为0,即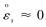
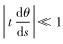
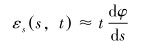
|
(6) |
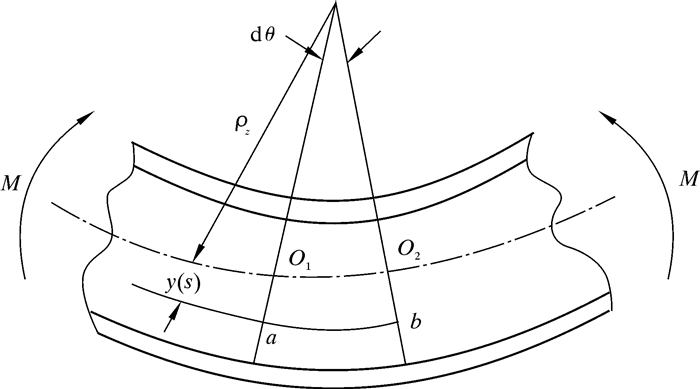
套管弯曲变形图如图 2所示。套管变形后,微段两端相对转过角度dθ,设中性层O1O2的曲率半径为ρz,则距中性层y(s)处纵向纤维ab的纵向应变为[21]:
|
| 图 2 套管弯曲变形图 Fig.2 Bending deformation diagram of casing |
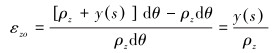
|
(7) |
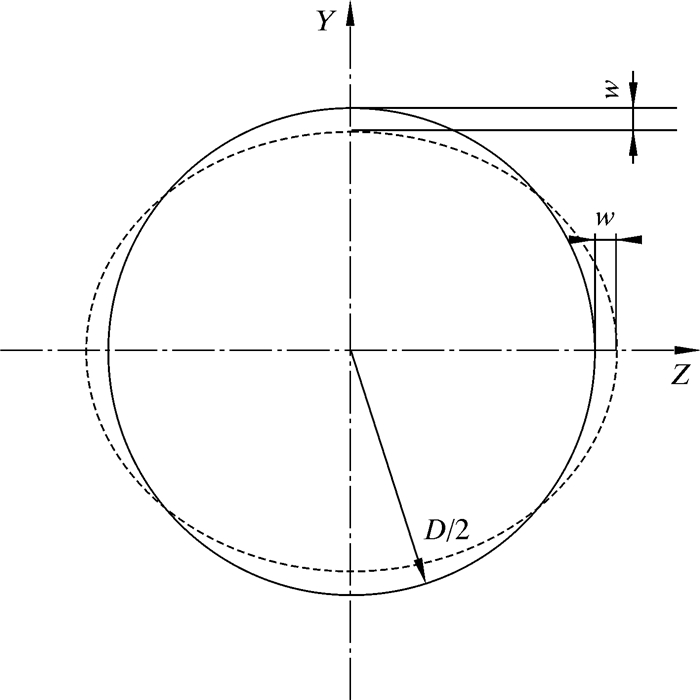
井眼曲率较小时,弯曲套管截面发生均匀扁化(见图 3),套管截面由圆形变为椭圆形[22]。假设套管的截面变形量为w,则截面扁化率ξ为:
|
| 图 3 套管截面扁化变形 Fig.3 Flattening deformation of the casing |
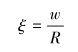
|
(8) |
式中:R为套管半径,m。
弯曲变形后,套管截面上任意一点的纵向应变为:

|
(9) |
式中:ψ为变形套管与水平方向的夹角,rad。
2 外载作用下套管应力分析通过对套管沿轴向和圆周方向发生扁化变形理论分析,得到扁化后套管截面沿轴线方向和圆周方向的应变表达式,并根据广义胡克定律,得到扁化套管截面纵向和环向应变简化公式。假设套管变形均匀且材料具有各向同性,由广义胡克定律,得到套管应力与应变之间的物理方程[23]:
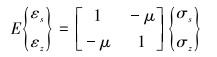
|
(10) |
式中:μ为泊松比,无量纲;E为套管材料弹性模量,Pa;σs为沿环向方向的应力;σz为沿轴向方向的应力。
化简式(10)得均布载荷作用下弯曲梁模型扁化套管截面环向和纵向应力表达式:

|
(11) |
根据最小势能原理,当截面扁化率使得套管变形能达到最小时,可得到套管截面扁化率与套管变形后弯曲曲率之间的关系。由外压作用下套管弹塑性状态下的弯曲微分方程近似解得到扁化套管任意截面产生的弯矩[24]:
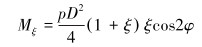
|
(12) |
式中:Mξ为横截面产生的弯矩,N·m;p为外压,Pa;D为套管外径,m。
套管所受三向应力为:
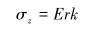
|
(13) |
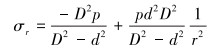
|
(14) |
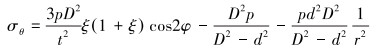
|
(15) |
扁化变形套管抗挤强度为:
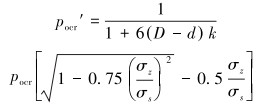
|
(16) |
式中: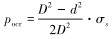
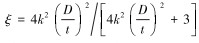
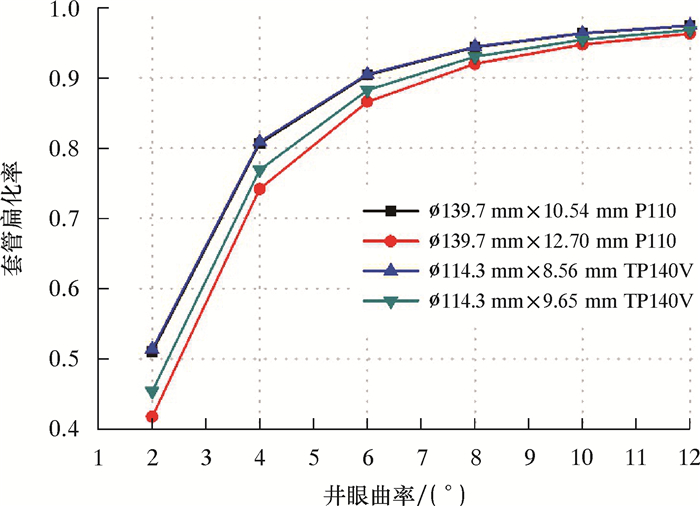
以ø139.7 mm×10.54 mm(12.7 mm)P110和ø114.3 mm×8.56 mm(9.65 mm)TP140V 4种规格套管为例,定量考察了扁化变形后套管的抗挤强度。图 4为不同井眼曲率时套管的扁化率。四种规格套管扁化率随井眼曲率变化规律一致,均为随井眼曲率的增加而非线性增加,开始时增长速率快,之后缓慢趋近于1。另外,由图 4还可以看出,薄壁套管易发生扁化变形,因此进行薄壁套管抗挤强度分析时更不能忽略扁化变形的影响。
|
| 图 4 4种规格套管扁化率随井眼曲率的变化曲线 Fig.4 Effect of the wellbore curvature on the flattening rate of the four kinds of casings |
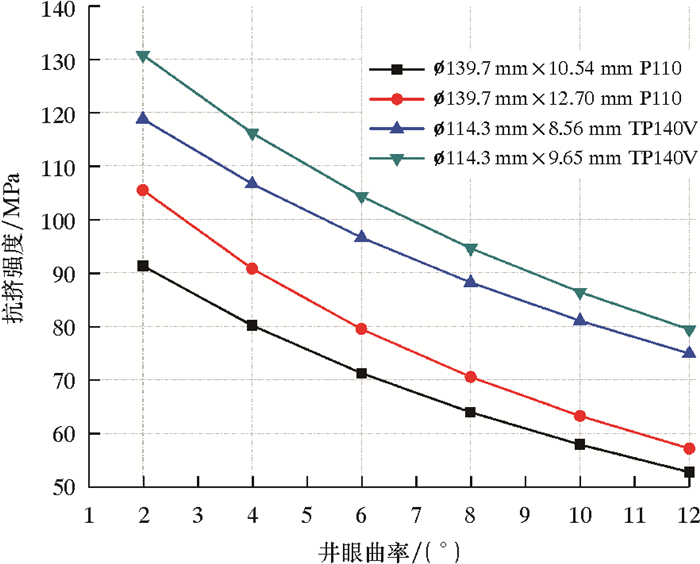
图 5和图 6分别为扁化变形后四种规格套管的抗挤强度随井眼曲率及轴向应力的变化曲线。
|
| 图 5 扁化套管的抗挤强度随井眼曲率的变化曲线 Fig.5 Effect of the wellbore curvature on the collapse strength of the flattened casing |

|
| 图 6 扁化套管的抗挤强度随轴向应力的变化曲线 Fig.6 The collapse strength of the flattened casing under different axial stresses |
由图 5和图 6可见:扁化套管的抗挤强度随井眼曲率和轴向应力的变化趋势一致,均为随其增加而非线性减小。当井眼曲率由每30 m井段2°增加到4°时,ø139.7 mm×12.7 mm P110套管抗挤强度由105.45 MPa降为90.77 MPa,降低14.68 MPa;当井眼曲率由每30 m井段8°增加到10°时,套管抗挤强度由70.51 MPa降为63.21 MPa,降低7.30 MPa。
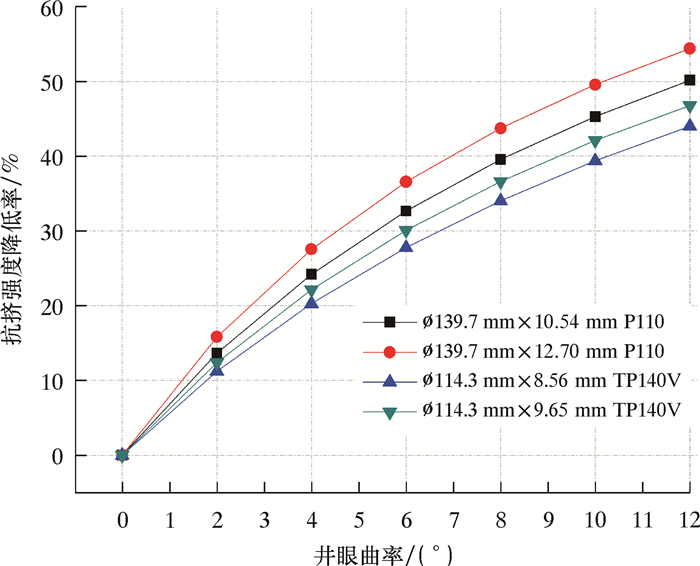
为直观地看出扁化套管抗挤强度降低率随井眼曲率的变化趋势,以未弯曲变形时套管的抗挤强度为基准值绘制曲线,结果如图 7所示。由图 7可见,扁化套管抗挤强度降低率随井眼曲率呈非线性增长,初始增速快,之后减慢。相同外径套管,厚壁套管抗挤强度的降低率较大。井眼曲率为每30 m井段6°时,ø139.7 mm×12.7 mm P110套管抗挤强度降低率为36.56%,ø139.7 mm×10.54mm套管抗挤强度降低率为32.66%;ø114.3mm×9.65mm TP140V套管抗挤强度降低率为30.08%,ø114.3 mm×8.56 mm套管抗挤强度降低率为27.75%。
|
| 图 7 扁化套管抗挤强度降低率随井眼曲率的变化曲线 Fig.7 Effect of the wellbore curvature on the reduction rate of the collapse strength of the flattened casing |
5 结论
借鉴扁化效应在圆管类结构中的分析思路,分析了4种规格套管扁化变形后抗外挤强度随井眼曲率的变化规律,得出如下结论:
(1) 套管扁化率随井眼曲率变化规律一致,均为随井眼曲率的增加而非线性增加,开始时增长速率快,之后缓慢趋近于1。
(2) 与厚壁套管相比较而言,薄壁套管易发生扁化变形。因此进行薄壁套管抗挤强度分析时不能忽略扁化变形的影响。
(3) 扁化套管的抗挤强度随井眼曲率与轴向应力的增加而非线性减小。
(4) 扁化套管抗挤强度降低率随井眼曲率呈非线性增长,初始增速快,之后减慢。相同外径套管,壁厚越大抗挤强度降低率越大。
| [1] |
窦益华, 张福祥. 高温高压深井试油井下管柱力学分析及其应用[J]. 钻采工艺, 2007, 30(5): 17-20. DOU Y H, ZHANG F X. Mechanical analysis of well testing down-hole string in deep well with HTHP and its application[J]. Drilling & Production Technology, 2007, 30(5): 17-20. DOI:10.3969/j.issn.1006-768X.2007.05.006 |
| [2] |
李子丰. 油气井杆管柱力学研究进展与争论[J]. 石油学报, 2016, 37(4): 531-556. LI Z F. Research advances and debates on tubular mechanics in oil and gas wells[J]. Acta Petrolei Sinica, 2016, 37(4): 531-556. |
| [3] |
API. Bulletin on formulas and calculations for casting, tubing, drill pipe, and line pipe properties exploration and production department: API BULLETIN 5C3[S]. Washington: API Publishing Services, 1999.
|
| [4] |
HUANG W J, GAO D L. A theoretical study of the critical external pressure for casing collapse[J]. Journal of Natural Gas Science & Engineering, 2015, 27: 290-297. |
| [5] |
徐德奎, 任虎彪, 李明飞, 等. 考虑弯矩和剪切影响的造斜段套管抗挤强度分析[J]. 石油机械, 2016, 44(9): 11-14. XU D K, REN H B, LI M F, et al. Analysis of collapsing strength of casing in buildup section considering bending moment and shear influence[J]. China Petroleum Machinery, 2016, 44(9): 11-14. |
| [6] |
申昭熙. 套管外压挤毁强度分析与计算[J]. 应用力学学报, 2011, 28(5): 547-550. SHEN Z X. Theoretic analysis and calculation of collapse strength of casing[J]. Chinese Journal of Applied Mechanics, 2011, 28(5): 547-550. |
| [7] |
贾宗文, 刘书杰, 耿亚楠, 等. 弯曲井段套管抗挤强度理论及试验研究[J]. 石油机械, 2018, 46(9): 100-105. JIA Z W, LIU S J, GENG Y N, et al. Theoretical and experimental study on the collapse strength of casing in curved well section[J]. China Petroleum Machinery, 2018, 46(9): 100-105. |
| [8] |
黄根炉, 陈忠帅, 马庆涛, 等. 弯曲井眼中套管抗挤强度计算[J]. 石油机械, 2011, 39(4): 38-40. HUANG G L, CHEN Z S, MA Q T, et al. The calculation of the casing collapse strength in bending hole[J]. China Petroleum Machinery, 2011, 39(4): 38-40. |
| [9] |
蒋官澄, 胡冬亮, 许发宾. 弯曲套管抗挤强度有限元ANSYS分析方法[J]. 断块油气田, 2009, 16(4): 134-136. JIANG G C, HU D L, XU F B. Finite element ANSYS analysis method of bending casing collapsing strength[J]. Fault-block Oil & Gas Field, 2009, 16(4): 134-136. |
| [10] |
KURIYAMA Y, TSUKANO Y, MIMAKI T, et al. Effect of wear and bending on casing collapse strength[R]. SPE 24597-MS, 1992.
|
| [11] |
董文涛, 吴萌, 张弘, 等. 体积压裂时套管弯曲应力放大计算分析[J]. 钻采工艺, 2018, 41(5): 9-11. DONG W T, WU M, ZHANG H, et al. Calculating casing bending stress amplification during SRV fracturing[J]. Drilling & Production Technology, 2018, 41(5): 9-11. DOI:10.3969/J.ISSN.1006-768X.2018.05.03 |
| [12] |
张华礼, 陈朝伟, 石林, 等. 流体通道形成机理及在四川页岩气套管变形分析中的应用[J]. 钻采工艺, 2018, 41(4): 8-11. ZHANG H L, CHEN Z W, SHI L, et al. Mechanism of how fluid passage formed and application in Sichuan shale gas casing deformation analysis[J]. Drilling & Production Technology, 2018, 41(4): 8-11. DOI:10.3969/J.ISSN.1006-768X.2018.04.03 |
| [13] |
马更生, 田雅琴, 黄庆学. 厚壁钢管压力矫直时的截面扁化计算[J]. 重型机械, 2012(2): 45-48. MA G S, TIAN Y Q, HUANG Q X. Calculation of cross section flattening for thick-walled steel pipe during pressure straightening[J]. Heavy Machinery, 2012(2): 45-48. DOI:10.3969/j.issn.1001-196X.2012.02.012 |
| [14] |
ZHANG L C, YU T X. An investigation of the brazier effect of a cylindrical tube under pure elastic-plastic bending[J]. International Journal of Pressure Vessels & Piping, 1987, 30(2): 77-86. |
| [15] |
鄂大辛, 郭学东, 宁汝新. 管材弯曲中应变中性层位移的分析[J]. 机械工程学报, 2009, 45(3): 307-310. E D X, GUO X D, NING R X. Analysis of strain neutral layer displacement in tube-bending process[J]. Journal of Mechanical Engineering, 2009, 45(3): 307-310. |
| [16] |
鄂大辛, 宁汝新, 古涛. 管材弯曲过程中的弹塑性变形分析[J]. 兵工学报, 2009, 30(10): 1353-1356. E D X, NING R X, GU T. Analysis on the elastic-plastic deformation during tube-bending process[J]. Acta Armamentarii, 2009, 30(10): 1353-1356. |
| [17] |
BRAZIER L G. On the flexure of thin cylindrical shells and other thin sections[J]. Proceedings of the Royal Society of London.Series A, Containing Papers of a Mathematical and Physical Character, 1927, 116(773): 104-114. |
| [18] |
钟华勇, 翟华, 李玉宝. 锆合金薄壁管三点弯校直中的截面扁化[J]. 塑性工程学报, 2011, 18(4): 97-100. ZHONG H Y, ZHAI H, LI Y B. The cross section flattening of zirconium alloys thin walled pipe in three points straightening[J]. Journal of Plasticity Engineering, 2011, 18(4): 97-100. DOI:10.3969/j.issn.1007-2012.2011.04.019 |
| [19] |
MICHAEL T C, VEERAPPAN A R, SHANMUGAM S. Effect of ovality and variable wall thickness on collapse loads in pipe bends subjected to in-plan bending closing moment[J]. Engineering Fracture Mechanics, 2012, 79(4): 138-148. |
| [20] |
MESHI T, ITO Y. Proposal of failure criterion applicable to finite element analysis results for wall-thinned pipes under bending load[J]. Nuclear Engineering and Design, 2012, 242: 34-42. DOI:10.1016/j.nucengdes.2011.09.032 |
| [21] |
余同希, 章亮炽. 塑性弯曲理论及其应用[M]. 北京: 科学出版社, 1992. YU T X, ZHANG L C. Plastic bending theory and its application[M]. Beijing: Science Press, 1992. |
| [22] |
薛嘉行, 姜开厚, 杨嘉陵, 等. 弹塑性圆管受纯弯载荷作用的实验研究[J]. 应用力学学报, 2000, 17(4): 50-57. XUE J X, JIANG K H, YANG J L, et al. An experimental research on elasto-plastc circular pipe under bending loads[J]. Chinese Journal of Applied Mechanics, 2000, 17(4): 50-57. DOI:10.3969/j.issn.1000-4939.2000.04.009 |
| [23] |
徐芝纶. 弹性力学简明教程[M]. 4版. 北京: 高等教育出版社, 2013. XU Z L. Concise course on elasticity[M]. 4th edition. Beijing: Higher Education Press, 2013. |
| [24] |
郝俊芳, 龚伟安. 套管强度计算与设计[M]. 北京: 石油工业出版社, 1987. HAO J F, GONG W A. Calculation and design of casing strength[M]. Beijing: Petroleum Industry Press, 1987. |



