2. 西南石油大学油气藏地质及开发工程国家重点实验室
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploration, Southwest Petroleum University
0 引言
随着环保和井场设置限制,丛式井场复杂井型越来越常见,在长裸眼井段套管下放常伴随出现不能到达预定位置、严重变形甚至断裂情况[1-4]。除了下放套管操作不够精细外,还与对复杂井型长裸眼井段套管下放动态过程产生的动力学行为认识和套管优化设计研究相对较少有直接关系。因此,急需开展下套管动态过程力学行为研究,这对规范指导现场操作非常重要。
国外学者对复杂井套管动态下放进行了相关研究。C.A.JOHANSICK[5]对全井段管柱受力进行了研究,建立了计算定向井钻柱扭矩和拉力的数学模型,为研究下套管受力情况奠定了理论基础。I.NETICHUK等[6]研究了大斜度井套管下放特征及改善井况作业措施。国内学者基于静力学理论,建立了井眼管柱二维或三维力学模型,并对实钻井眼轨迹下套管轴向力和扭矩等进行了分析[7-11]。
国内外学者在套管下放受力计算模型方面取得了一些经典的公式与理论,但是对于复杂井型套管动态下放中的动力学行为研究还是较少。因此,本文基于动力学理论,对新疆油田M井套管下放遇阻问题开展了相应的研究,分析了套管下放到不同井深时全井段套管动态变形及受力,并在此基础上对套管上提冲放过程进行了仿真模拟。研究结果为指导套管顺利下放提供了理论依据。
1 套管下放力学分析套管在动态下放过程中,除了受浮重、钻井液黏阻力以及克服非光滑井壁作用力外,还受动态下放的动载荷和井口上提冲放惯性力等附加力作用。
1.1 套管下放动载荷在下套管过程中,根据下放速度计算套管动载荷Fd的公式为[12]:
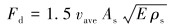
|
(1) |
式中:vave为下套管的平均速度,m/s;As为套管柱横截面积,m2;E为套管钢材的弹性模量,Pa;ρs为套管钢材的密度,kg/m3。
1.2 井口上提套管瞬间冲放惯性力当套管自由下放受阻后,现场通常采用“上提冲放”作业,被瞬间释放的套管承受井口冲放惯性力。根据作用力和反作用力关系,此时井口套管瞬间冲放惯性力等于上提力,即:

|
(2) |
式中:Fg为井口套管被瞬间冲放时的惯性力,Fs为上提作用时井口套管受到的上提力,单位均为kN。
2 套管动态下放过程研究 2.1 建立套管动态下放过程模型M井是一口典型复杂井型长裸眼水平井,实际井深5 876 m,最大井斜角为90.6°,最大狗腿度为每30 m弯曲7.5°,水平位移为2 055 m。该井从3 500 m附近造斜并扭方位,方位角从295°变到110°,水平井A靶井深约4 200 m。二开套管下到3 100 m,三开套管下到5 860 m,裸眼井段长2 760 m。三开下入套管钢级为TP125V,外径127 mm,壁厚11.1 mm。
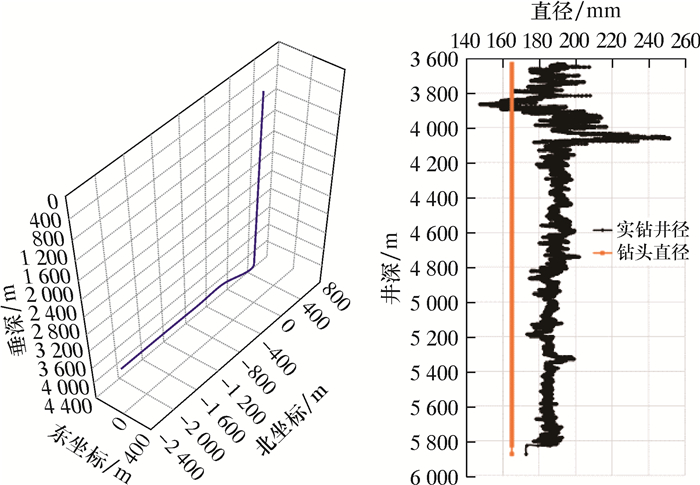
假设井眼横截面为规则圆形,井眼轨迹平滑过渡,根据如图 1所示的实际井眼轨迹、井径、井身结构和套管串结构建立三开全井段套管下放过程的三维有限元力学模型。套管与上层套管和裸眼井壁为广义接触,裸眼井段套管与岩石井壁的接触摩擦因数为0.43,二开套管与三开套管的接触摩擦因数为0.30。模型考虑套管浮重、下放动载荷、钻井液阻尼效应、套管屈曲变形及附加阻力,井口套管定速下放。
|
| 图 1 M井实钻井眼轨迹及井径曲线 Fig.1 Well trajectory and caliper curve of Well M |
2.2 套管定速下放过程动力学行为分析
套管在重力作用下顺利下放进入水平井段A靶(井深4 200 m)及水平井段,随着下放深度的增加,套管动力学变形和摩阻也不断变化。
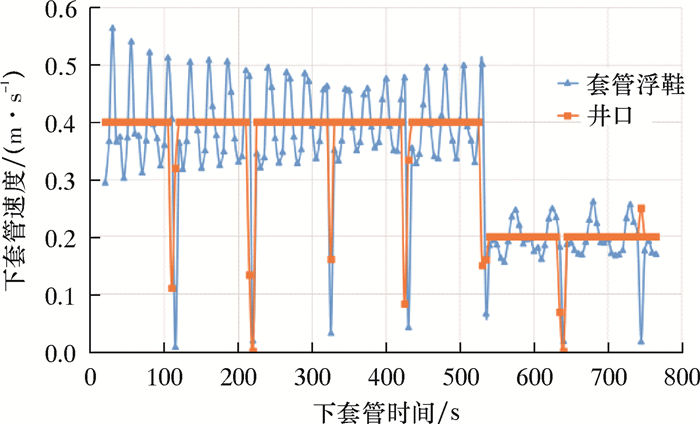
2.2.1 套管下放至5 000 m井深根据建立的全井段套管下放模型,初始设定井口套管下放速度为0.4 m/s,相当于每分钟下放2根套管。当套管串下放到5 000 m井深时,套管最末端浮鞋的移动速度在0.4 m/s上下呈现周期性波动,而且当井口套管速度设定为0.0 m/s时(类似于接套管作业停顿),套管浮鞋速度也迅速降低为0.0 m/s,如图 2所示。由图 2可知:井口套管和浮鞋位移基本同步,整个套管串下放顺畅;当把井口套管速度降低为0.2 m/s(相当于每分钟下放1根套管)时,套管浮鞋也呈现类似波动,但是波动幅度变小,说明套管更加平稳地下放移动,套管相对安全。
|
| 图 2 套管下放到5 000 m井深附近的速度 Fig.2 The casing running speed at the depth of 5 000 m |
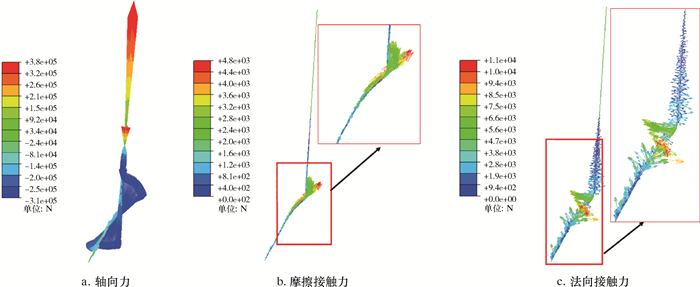
取出在0.2 m/s下放速度下某任意时刻的全井段套管柱轴向力、摩擦阻力和接触力进行分析,结果如图 3所示。造斜段至水平段套管轴向力为压缩力,全井段套管最大压缩力在斜井段处,最大拉力在井口处。由于实钻井眼轨迹和井径变化的复杂性,在造斜点以下扭方位井段处的套管柱在浮重、摩阻和下放轴向力等复杂力学环境下靠向不同方位的井壁,造成接触力。套管与井壁的法向接触力为正压力,切向接触力为套管摩擦阻力。由图 3可知,在扭方位斜井段处的套管柱摩阻力最大,同时造斜点以上部分直井段套管与井壁发生了接触,且接触方位分布复杂,充分说明了套管在动态下放过程中受力变形十分复杂,井眼轨迹和井径对套管下放的影响极大。
|
| 图 3 套管下放到5 000 m井深、下放速度为0.2 m/s时的受力分析 Fig.3 Stress analysis of the casing down to 5 000 m with the running speed of 0.2 m/s |
2.2.2 套管下放至5 400 m井深
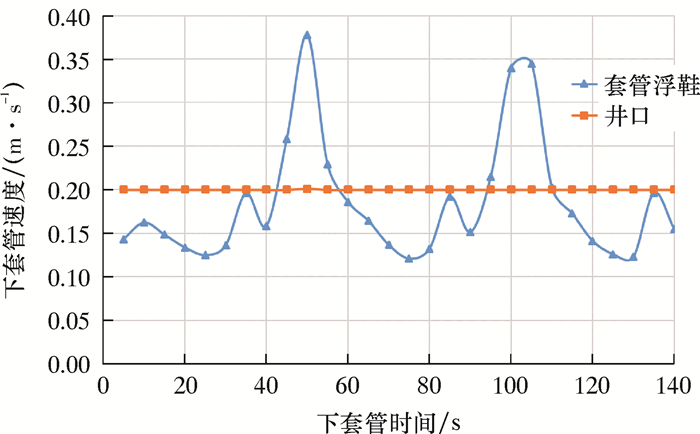
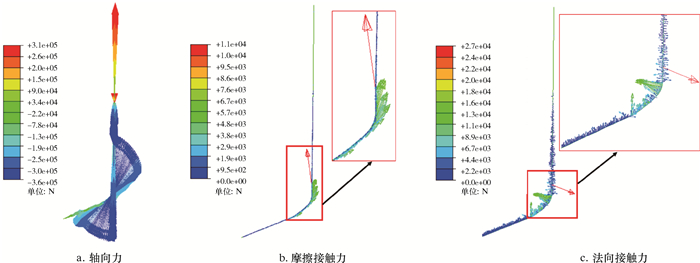
随着套管下放深度增加到5 400 m,套管浮鞋和井口位置的速度还能保持大体同步,此时,套管浮鞋处速度在0.2 m/s上下呈周期性波动,说明在井口持续稳定速度下放时,被压缩套管段经受弹性能量积累、释放和再积累的周期变化,如图 4和图 5所示。但是从图 5也可看出,套管下放到5 400 m后井口轴向拉力减小,弯曲井段轴向压缩力增加到3.6×105 N。同时,局部井段套管摩阻力和法向接触力明显增大,说明套管下放动力在不断减小。而且套管接触矢量方向指向各个方向,直井段套管发生了明显的屈曲现象,并且从轴向力的大小上可知,该段套管柱的屈曲形式包括正弦屈曲、不稳定屈曲甚至螺旋屈曲。
|
| 图 4 套管下放到5 400 m井深附近的速度 Fig.4 The casing running speed at the depth of 5 400 m |
|
| 图 5 套管下放到5 400 m井深、下放速度为0.2 m/s时的受力分析 Fig.5 Stress analysis of the casing down to 5 400 m with the running speed of 0.2 m/s |
2.2.3 套管下放至5 800 m井深
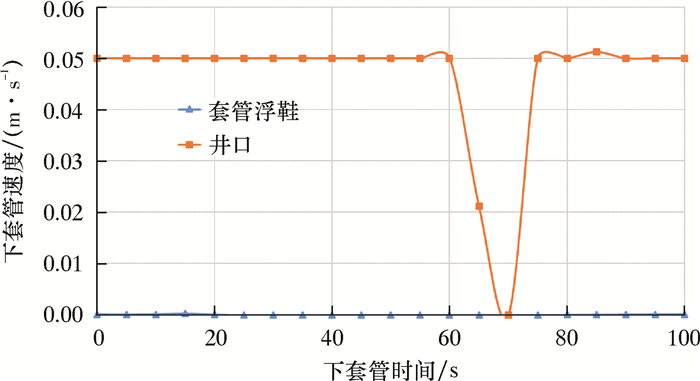
套管下放至5 800 m井深时,井口套管下放速度降低至0.05 m/s(相当于每分钟下放3 m),但套管浮鞋处速度接近0.0 m/s,即套管柱低端没有移动,如图 6所示,而且期间设定了井口暂停下放(下放速度为0.00 m/s),浮鞋套管的速度也没有受到任何影响。这说明直井段套管压缩产生的弹性能量不足以推动套管移动,同时也没有传递到套管浮鞋处。
|
| 图 6 套管下放到5 800 m井深附近的速度 Fig.6 The casing running speed at the depth of 5 800 m |
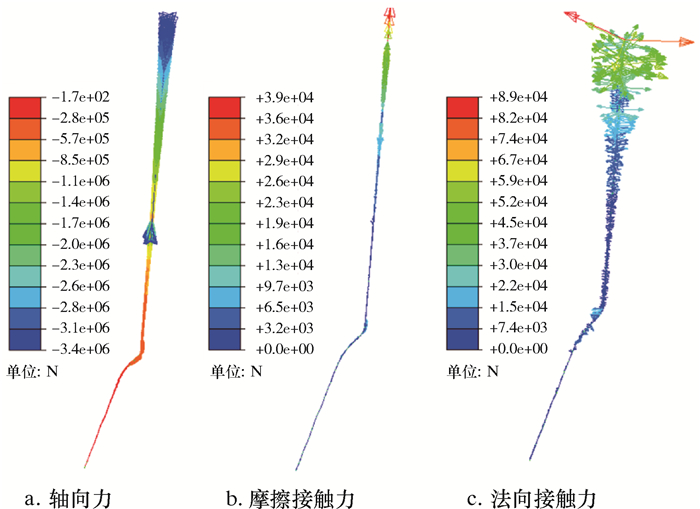
图 7为套管下放到5 800 m井深附近的受力矢量图。由图 6和图 7可知,全井段套管柱承受压缩作用的轴向力,发生了屈曲变形,而且井口持续施加的下放速度导致直井段上部套管发生严重弯曲。在该位置套管法向接触力和摩擦力矢量指向不同方向,其中发生严重螺旋屈曲的套管与井壁接触,产生了足够大摩阻力,限制了套管移动,进而发生了自锁现象。自锁段的上部套管下放动力不能将动力传递到下部井段,也不能继续推动套管柱整体下放,而井口下放作用力只持续作用到自锁点以上套管并加剧螺旋屈曲,最终导致套管下放困难。
|
| 图 7 套管下放到5 800 m井深时的受力分析 Fig.7 Stress analysis of the casing down to 5 800 m |
由此可见,套管能否顺利下放不仅取决于摩阻与重力,还取决于屈曲现象的严重程度。套管自锁通常在直井段,而且其临界点非常复杂,几乎与所有工况参数有关。
综上所述,通过对M井套管下放5 000~5 800 m过程动态行为的分析,套管柱在井深5 400 m前可以在足够大的弹性压缩能作用下下放套管,但之后随着套管摩阻的增大和直井段套管螺旋屈曲的加剧,导致无法传递足够的能量驱动套管柱继续下放,最终使得套管下放不能到达预定位置,模拟结果与现场套管下放情况一致。
2.3 冲放套管下放过程动力学行为分析当套管无法顺利下放时,现场通常采用辅助方法强迫套管下放,例如施加旋转、轴向冲击力或顶驱推力等促使套管克服摩阻,其中“上提冲放”套管是最经济的常用措施[13]。本文在M井套管柱于5 800 m处下放遇阻的基础上,对现场采取“上提冲放”的动态过程进行模拟分析。
套管的“上提冲放”是一个多次周期循环的作业过程,本文仅对其中两个周期过程建立了相应的模型,包括上提1.1×106 N作用力并快速释放,套管柱稳定后井口下压1.0×105 N并快速释放,以及再次上提1.1×106 N作用力并快速释放。整个模型相当于完整模拟了2次“上提冲放”套管和1次下压套管的过程,进而分析“上提冲放”过程对套管的受力、变形及套管柱优化的影响。
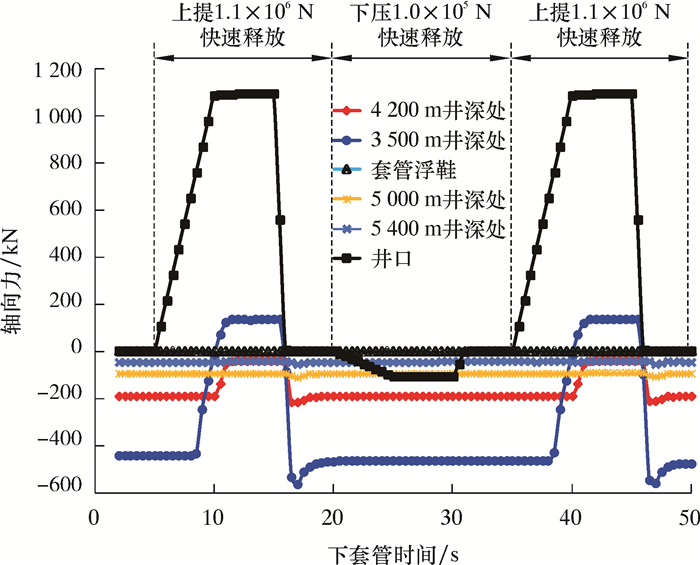
图 8为“上提冲放”过程套管轴向力的变化曲线。由图 8可知,井口套管、造斜点3 500 m处套管和4 200 m处(水平井A靶)套管在整个“上提冲放”模拟过程中影响较大,尤其是冲放瞬间对直井段和弯曲井段套管有明显影响。然而,从5 000、5 400以及5 800 m井深浮鞋处的套管轴向力来看,“上提冲放”措施基本没有引起水平井段套管轴向力的变化。因此,“上提冲放”措施对水平段套管的影响很小,而对直井段和扭方位弯曲井段套管影响较大。
|
| 图 8 “上提冲放”过程套管轴向力的变化曲线 Fig.8 The axial stress curve of the casing during "uplifting and fast running" |
分析可知,第一次“上提冲放”作业和第二次“上提冲放”作业套管的轴向力变化规律基本相同,井口下压1.0×105 N对下部套管基本没有影响,说明“上提冲放”作业对管柱本体无明显影响。
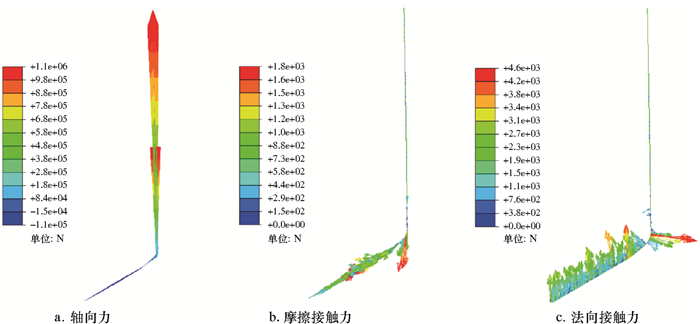
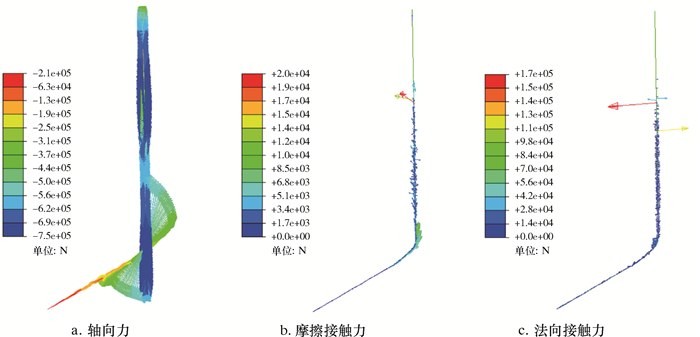
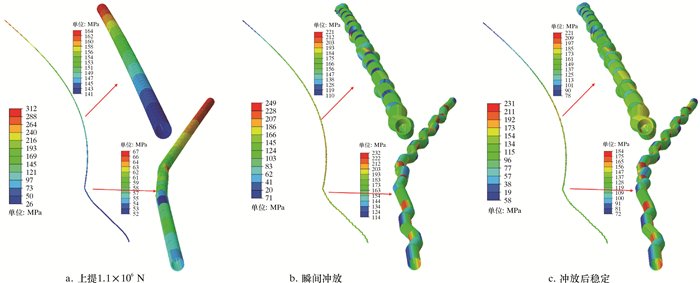
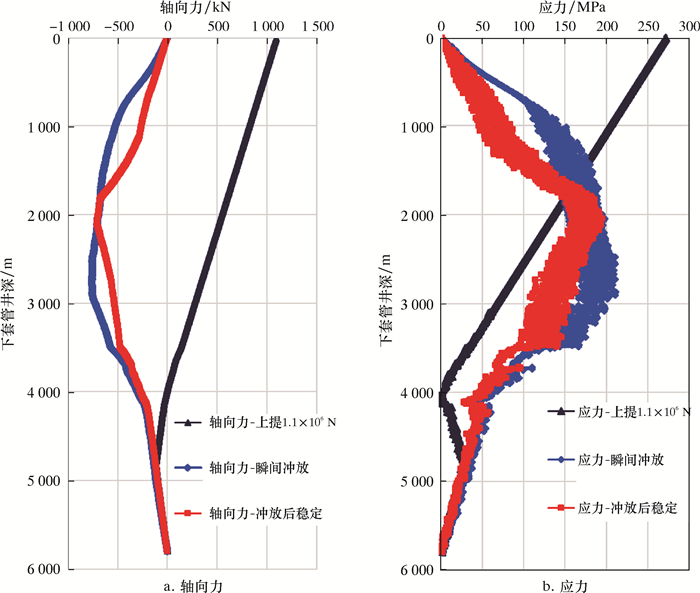
图 9~图 12为不同时刻下全井段套管的受力分布云图。由图 9~图 12可知:当套管上提1.1×106 N时,直井段和弯曲井段套管基本都承受拉力;当套管恢复为拉直状态,套管轴向力和应力表现为线性分布,全井段套管与井壁的接触点减少,接触力也随之减小,而水平井段套管则保持之前的接触和变形状态;当井口套管瞬间冲放,以1.1×106 N的瞬间冲击力作用在整个井段套管上时,套管轴向力、应力和接触力发生极大变化;瞬间冲放,套管全井段受到轴向压缩力作用,1 000 m以下套管发生明显屈曲变形,1 800 m附近井深以下套管发生螺旋屈曲与井壁接触,尤其在2 000 m井深附近套管可能发生严重螺旋屈曲自锁现象,此井段套管接触力和应力异常变化且数值最大;此外,3 500 m造斜点以下扭方位井段,套管接触和弯曲幅度较大;当瞬间冲放后,套管会恢复到稳定状态,全井段套管轴向力、应力和变形会相应减低并保持稳定,但套管总体变形屈曲状态和接触状态没有发生根本变化。
|
| 图 9 上提1.1×106 N时刻全井段套管受力矢量图 Fig.9 The full wellbore casing stress vector at the uplifting time of 1.1×106 N |
|
| 图 10 瞬间冲放时刻全井段套管受力矢量图 Fig.10 The full wellbore casing stress at instantaneous fast running time |
|
| 图 11 全井段套管应力云图 Fig.11 The full wellbore casing stress distribution |
|
| 图 12 套管沿井深受力分布图 Fig.12 Distribution of the casing stress along the wellbore |
虽然上提冲放加剧了套管的屈曲变形和应力状态,甚至出现了螺旋屈曲自锁,但是全井段套管本体最大应力为提拉套管时的270 MPa,远低于Q125钢级套管的屈服强度,套管在“上提冲放”整个过程中处于弹性变形,在下一轮“上提冲放”套管作业时又会恢复套管弹性状态。这说明理想套管在单次“上提冲放”作业下不会造成损伤和破坏。但是实际作业中,不能排除含缺陷和接头的套管,其缺陷与接头处易发生应力集中,在周期载荷作用下会出现疲劳起裂甚至断裂的现象。
综上所述,通过对M井“上提冲放”过程动态行为的分析,“上提冲放”主要对直井段套管产生较为严重的影响,且在2 000 m附近井段可能产生严重螺旋屈曲自锁,而直井段套管仍处于弹性变形,能够承受单次“上提冲放”作业作用。但是,进行多次大吨位“上提冲放”作业,可能会造成含缺陷套管和接头疲劳失效事故。
3 结论(1) 建立了全井段套管柱动态下放的有限元力学模型。通过分析M井套管动态下放过程,套管顺利下放的因素包括套管摩阻与重力的关系,也包括套管是否产生严重螺旋屈曲而自锁。
(2) 在M井套管柱于5 800 m井深处无法顺利下放的基础上,开展了“上提冲放”措施动态过程分析。研究结果表明,单次“上提冲放”作业不会对套管造成损伤和破坏,但进行多次大吨位“上提冲放”作业可能使部分套管出现缺陷和接头应力集中,进而导致疲劳开裂甚至断裂的现象。
(3) 建立的套管动态下放模型及冲放下套管动力学分析,为复杂长裸眼井段套管顺利下放提供了理论依据,对规范现场施工具有指导意义。
| [1] |
林家昱, 王志月, 冉辉, 等. 水平井下套管受力分析研究[J]. 中国石油和化工标准与质量, 2014, 34(1): 97. LIN J Y, WANG Z Y, RAN H, et al. Stress analysis of horizontal downhole casing[J]. China Petroleum and Chemical Standard and Quality, 2014, 34(1): 97. DOI:10.3969/j.issn.1673-4076.2014.01.095 |
| [2] |
卢继锋.水平井井下作业管柱受力分析及应用研究[D].北京: 中国石油大学(北京), 2014. LU J F. Research of mechanical analysis and application of downhole operation string in horizontal well[D]. Beijing: China University of Petroleum(Beijing), 2014. |
| [3] |
张映辉, 王青, 李振, 等. 委内瑞拉奥里诺科重油带水平井套管下入技术[J]. 石化技术, 2016, 23(5): 120. ZHANG Y H, WANG Q, LI Z, et al. Running casing in horizontal well in heavy oil reservoir in Venezuela[J]. Petrochemical Industry Technology, 2016, 23(5): 120. DOI:10.3969/j.issn.1006-0235.2016.05.095 |
| [4] |
李庆明. 水平井套管下入摩阻力学分析[J]. 石油工业技术监督, 2018, 34(6): 27-29. LI Q M. Friction resistance analysis of casing in horizontal well[J]. Technology Supervision in Petroleum Industry, 2018, 34(6): 27-29. DOI:10.3969/j.issn.1004-1346.2018.06.008 |
| [5] |
JOHANSICK C A. Torque and drag in direction wells prediction and measuremen[J]. Journal of Petroleum Technology, 1984, 36(6): 987-992. DOI:10.2118/11380-PA |
| [6] |
NETICHUK I, SUVOROV A, GALIMOV A. Special features of casing running and cementing in ERD wells[R]. SPE 181947, 2016.
|
| [7] |
徐苏欣, 段勇, 雒维国. 大位移井下套管受力分析和计算[J]. 西安石油大学学报(自然科学版), 2001, 16(4): 72-74. XU S X, DUAN Y, LUO W G. Analysis and calculation of the forces exerting on casing in the process of running into high angle deviated hole[J]. Journal of Xi'an Petroleum Institute (Natural Science Edition), 2001, 16(4): 72-74. DOI:10.3969/j.issn.1673-064X.2001.04.020 |
| [8] |
曲永哲, 李悦钦, 史海涛, 等. 水平井下套管计算模型及应用[J]. 机械, 2008, 35(5): 26-28. QU Y Z, LI Y Q, SHI H T, et al. Casing running physical model and its application in horizontal wells[J]. Machinery, 2008, 35(5): 26-28. |
| [9] |
赵达壮, 刘坤芳. 水平井套管的动态力学分析[J]. 力学与实践, 1997, 19(2): 38-40. ZHAO D Z, LIU K F. Dynamic mechanical analysis of horizontal well casing[J]. Mechanics and Practice, 1997, 19(2): 38-40. |
| [10] |
陈鹏举.页岩气水平井套管柱下入摩阻分析与控制技术研究[D].北京: 中国石油大学(北京), 2013. CHEN P J. Downhole drag analysis and control techniques for casing running operations in horizontal well for shale gas[D]. Beijing: China University of Petroleum(Beijing), 2013. http://cdmd.cnki.com.cn/Article/CDMD-11414-1018700502.htm |
| [11] |
张宏伟, 王希, 艾志久, 等. 深斜井注水管柱下放力学模型研究[J]. 石油机械, 2014, 42(12): 102-105, 110. ZHANG H W, WANG X, AI Z J, et al. Mechanical model of injection line setting in deep inclined well[J]. China Peroleum Machinery, 2014, 42(12): 102-105, 110. DOI:10.3969/j.issn.1001-4578.2014.12.024 |
| [12] |
龚龙祥.大位移井套管柱强度设计研究[D].成都: 西南石油大学, 2007. GONG L X. Strength design of casing string in extended-reach well[D].Chengdu: Southwest Petroleum University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10615-2008016791.htm |
| [13] |
宋执武, 陈鹏举, 高德利. "上提下冲"下套管作业方法的力学分析[J]. 石油管材与仪器, 2016(6): 45-48. SONG Z W, CHEN P J, GAO D L. Mechanics analysis of "lift and free fall" casing running method[J]. Petroleum Tubular Goods & Instruments, 2016(6): 45-48. DOI:10.3969/j.issn.1004-9134.2016.06.011 |


