2. 中国石油大学(北京)石油工程学院;
3. 北京工业大学;
4. 中海油研究总院有限责任公司;
5. 长江大学研究生院
2. College of Petroleum Engineering, China University of Petroleum(Beijing);
3. Beijing University of Technology;
4. CNOOC Research Institute Co., Ltd.;
5. Graduate School of Yangtze University
0 引言
控压钻井技术要求对钻井过程中各个环节实现精细环空压力控制[1],而建立精确的水力学模型则是控压钻井技术的基础理论。钻前工艺参数选取、钻中工艺参数调整以及压力控制方案制定都是依据井筒水力学模型[2]。但是,水力学模型只是针对真实钻井情况的简化计算,其本身存在一定的局限性,对于现场作业中常见的井径不规则、钻柱偏心情况以及高温高压下钻井液物性参数变化难以准确描述。由于井筒流动状态的高度复杂性,导致单纯依靠水力学模型来精确描述井筒流体流动难以实现,计算结果与真实值往往存在较大误差[3]。
目前已有研究[4-11]主要利用卡尔曼滤波和最小二乘法算法,结合井筒水力学模型,建立井下压力解释模型,但其核心原理均是通过对比PWD单点测量数据与模型计算数据的差异,在地面进行综合解释。但单点数据解释模型反演参数过于单一、不确定性问题突出、无法准确反映压力的变化。鉴于此,本文提出了结合无迹卡尔曼滤波技术与水力学模型的井下双测点压力实时解释模型,采用该模型可以实现复杂井筒流动下井下压力实时校正计算,并具有较高的计算精度;同时探索分析了双测点间距与反演精度之间的关系,优选了合理的双测点间距。研究结果可为井下双测点测量装置的研制与现场应用提供理论指导。
1 无迹卡尔曼滤波技术无迹卡尔曼滤波技术是非线性最优估计领域的一项重要研究成果。1997年,S.J.JULIER等[12]根据确定性采样的基本思路提出了无迹卡尔曼滤波,此后学者E.A.WAN等[13]进一步对该技术进行了完善。相比非线性估计中的另一典型代表——扩展卡尔曼滤波,无迹卡尔曼滤波采用无迹变换取代局部线性化,取消了对系统模型的限制条件,既不要求状态函数和测量函数必须连续可微,也不需要计算繁琐的雅克比矩阵,使得计算精度和速度大大提高,工程应用难度降低。
研究中,考虑如下非线性系统。
状态方程:
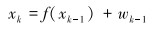
|
(1) |
测量方程:
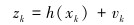
|
(2) |
式中:xk为n维的状态向量;f(·)为非线性系统状态函数;zk为测量向量;h(·)为非线性测量函数,本文中即为井筒水力学校正模型;wk、vk分别为系统的过程噪声和测量噪声,均满足零均值高斯白噪声分布wk~N{0,Qk}和vk~N{0, Rk},且两者互不相关。
假设已知状态在前一时刻的状态估计值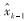
(1) 设定初始时刻的状态统计量为:
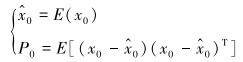
|
(3) |
式中:状态初始值x0与wk、vk彼此相互独立,且服从高斯分布。
(2) 构造Sigma点及其权值。按照UT变换中选择的比例修正对称采样策略,由前一时刻的状态估计值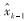
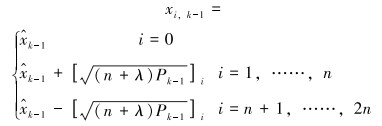
|
(4) |

|
(5) |
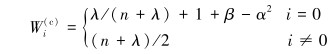
|
(6) |
式中:Wi(m)为均值加权所用的权值;Wi(c)为协方差加权所用的权值;α为扩展因子,一般取[0, 1];λ为比例因子,λ=α2(n+κ)-n;κ为可调参数,对于高斯分布,当状态向量为n维时,取κ=3-n;β为描述状态向量先验分布信息的参数,对于高斯分布,其最优值为2。
(3) 状态更新。利用状态方程传递Sigma点为xi, k/k-1,进一步预测状态均值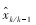

|
(7) |
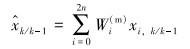
|
(8) |
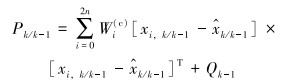
|
(9) |
(4) 测量更新。利用测量方程传递Sigma点为zi, k/k-1,用以预测测量值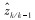
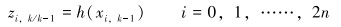
|
(10) |
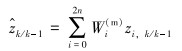
|
(11) |
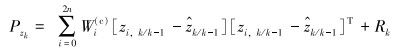
|
(12) |
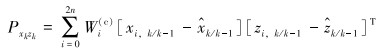
|
(13) |
计算卡尔曼增益矩阵Kk,然后基于获取的新的测量值zk,对当前时刻的状态均值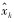
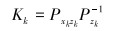
|
(14) |
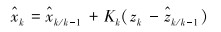
|
(15) |
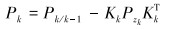
|
(16) |
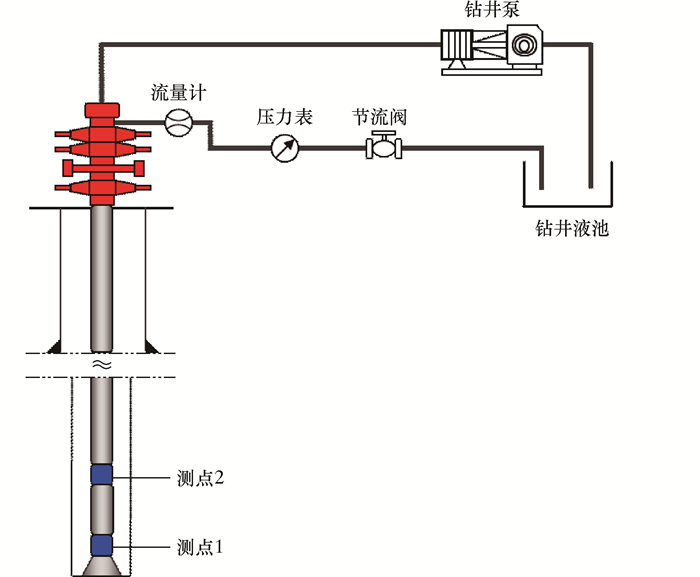
井下双测点压力测量是指在井底近钻头处钻柱的两端安装两个压力传感器,传感器之间采用有线钻杆(智能钻杆)的方式连接,这样就可以同步获取不同时间双测点的压力数据,如图 1所示。
|
| 图 1 井下双测点压力解释示意图 Fig.1 Schematic diagram of pressure interpretation with downhole dual point measurement |
正常工况下,选取井下双测点压力值作为测量数据,可表示为:
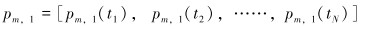
|
(17) |
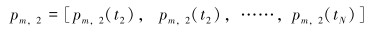
|
(18) |
式中:p表示井筒压力;t1, t2, ……, tN表示测量数据对应的N个时刻点;下标m表示测量数据,下标1和2分别表示井下的测点1和2。
在控压钻井中,由于地面节流管汇中节流阀的动作产生一定的回压值,所以井底压力实际上由静液柱压力、摩阻压力和井口回压3部分组成,如式(19)所示。
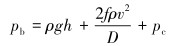
|
(19) |
式中:pb为井底压力;pc为井口回压;g为重力加速度,取9.81 m/s2;h为垂深;ρ为钻井液密度;f为摩阻系数;v为流速;D为水力直径。
从式(19)可以看出,与井底压力相关的参数包括钻井液密度、流变参数、摩阻系数、流速和水力直径等。钻井液密度和流变参数沿井筒分布不是一成不变,它们随着温度压力的变化而变化。高温高压钻井液密度和流变参数模型的建立通常由室内试验数据拟合得到相应的经验公式。然而经验公式不具备普适性,不同钻井液体系、配方甚至试验条件都会对拟合结果产生一定的影响,类似地还有以经验公式为准的紊流流态下的摩阻系数计算。
井口回压可以通过井口压力表精确测量获得,而静液柱压力和摩阻压力均与上述参数相关。为了准确描述井底压力变化,减小模型参数输入值与真实值之间的偏差,分别在静液柱压力和摩阻压力部分引入密度校正因子和摩阻校正因子。校正后的井筒水力学模型如下:
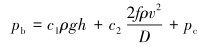
|
(20) |
式中:c1为密度校正因子,c2为摩阻校正因子。
采用非牛顿流体的广义流性指数n′研究方法进行环空压耗计算。具体为:当广义雷诺数Reg≤3 470-1 370n′时,流态为层流,f=16/Reg;当广义雷诺数Reg>3 470-1 370n′时,流态为紊流,选用考虑表面粗糙度影响的Reed-Pilehvari公式[14]求取f。
将密度校正因子和摩阻校正因子作为模型的反演参数,不同时刻的反演参数可表示为:
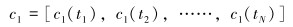
|
(21) |

|
(22) |
对于常规的单测点压力解释而言,单点压力测量只能输出一种反演参数,即密度校正因子或者摩阻校正因子,两者选其一。然而双测点压力解释可以输出水力学校正模型中两种反演参数,相比单测点压力解释而言,其反演参数更加全面,建立的井筒水力学反演模型对应的物理意义更加明确。
无迹卡尔曼滤波是一类可实时计算的递推算法,主要针对模型中的状态变量进行实时校正,状态变量即是反演参数。基于无迹卡尔曼滤波解释模型中的状态变量(x)和测量变量(z)确定如下,下标k表示k时刻。
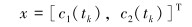
|
(23) |
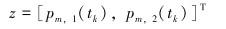
|
(24) |
基于以上分析建立井筒水力学解释模型,开展井下双测点压力实时解释数值模拟计算。首先预设1组密度校正因子和摩阻校正因子作为反演参数真实值,然后利用建立的井筒水力学模型来模拟井下双测点压力值,并将其作为测量数据。因此,本文的测量数据采用人工合成数据,然后再利用解释模型计算相关参数反演值,使得模型测量参数的计算值与测量值相吻符合。
井下双测点压力传感器分别安装在近钻头处钻柱的两端,传感器之间采用有线钻杆(智能钻杆)的方式连接,保证了双测点压力测量数据的同步传输,这样双测点距离以单一钻柱长度(10 m)为基本单位。为了分析双测点距离对反演结果的影响,将双测点距离分别设置为10、20和30 m,针对不同的双测点距离开展模型反演计算。
模拟井基础数据如下:井深3 000 m,套管下深2 200 m,钻铤长度200 m,套管直径228.5 mm,井眼直径215.9 mm,钻杆内外径108.6/127.0 mm,喷嘴面积660 mm2,排量30 L/s,钻井液密度1 180 kg/m3,稠度系数0.37 Pa·sn,流性指数0.68,动切力3.84 Pa,每100 m地温梯度2.66 ℃,井口回压1 MPa。滤波中3个关键参数的取值为:α=0.1,β=2,κ=1。另外,密度校正因子和摩阻校正因子对应的系统噪声的标准差设置为0.05,而压力测量噪声的标准差设为0.000 2。因此,校正模型中的协方差矩阵为Q=diag[0.052, 0.052],R=diag[0.000 22, 0.000 22]。
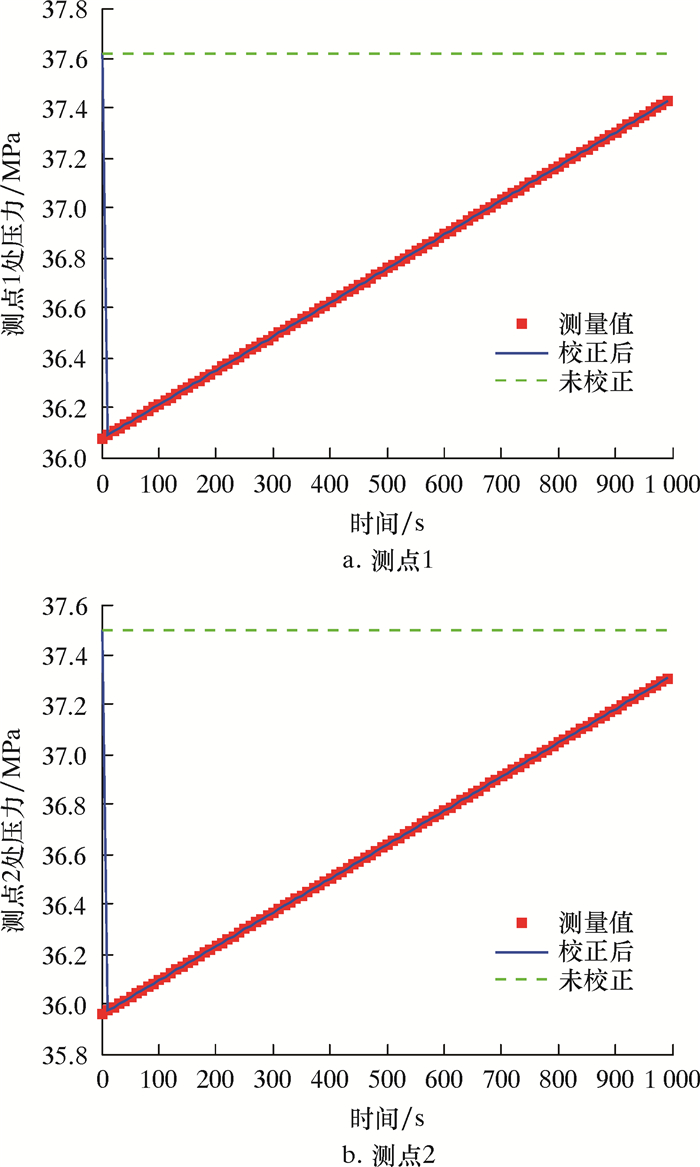
图 2给出了双测点压力计算结果和测量结果。由图 2可以明显看出,测点1和测点2处压力的校正曲线和测量曲线基本重合,说明校正值和测量值相差很小。因此,在图 2中主要以双测点距离10 m为例给出了双测点压力的变化规律。井底3 000 m(测点1)处的压力和井深2 990 m(测点2)处的压力变化基本一致,随着时间的推移,双测点压力均逐渐增加。需要说明的是,预设的井筒压力与实际钻井过程中井筒压力变化相同。这是因为在实际钻井过程中,受井筒循环温度场的影响[15],井底温度会逐渐降低,钻井液密度会相应变大,从而井底压力增加。此外,测点1和测点2处的压力初值分别为37.6和37.5 MPa,未校正情况下的双测点压力均维持为初值不变。
|
| 图 2 双测点压力计算值与测量值对比 Fig.2 Comparison of the calculated values and measured pressures with the two measuring points |
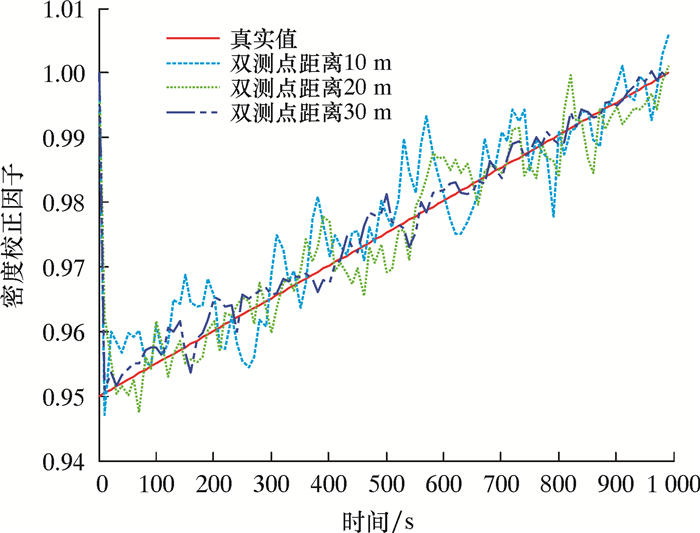
图 3和图 4分别给出了不同双测点距离的密度校正因子和摩阻校正因子反演值与真实值的对比。
|
| 图 3 不同双测点距离时密度校正因子反演值与真实值的对比 Fig.3 Comparison of the inversion value with the true value of the density correction factor under different dual measuring point distances |

|
| 图 4 不同双测点距离时摩阻校正因子反演值与真实值的对比 Fig.4 Comparison of the inversion value with the true value of the friction correction factor under different dual measuring point distances |
由图 3和图 4可知,在0~1 000 s时间内,预设的密度校正因子真实值由0.95线性增加至1.00,而预设的摩阻校正因子真实值由1.10线性降至0.90。密度校正因子和摩阻校正因子的初值均为1.00,初期校正因子变化规律与测量参数(双测点压力)基本一致,其反演值快速接近其真实值,然而之后会在真实值的附近上下波动,且不同的双测点距离对应的波动幅度不一样。双测点距离30 m的反演精度大于双测点距离20 m,而双测点20 m的反演精度大于双测点距离10 m。随着双测点距离的增加,模型的反演精度随之提高。其原因是双测点之间的距离越大,双测点的压力差值越大,两点之间可识别的差异化信息越多,从而提高了解释模型的解释精度。此外,密度校正因子的符合度明显高于摩阻校正因子,这是密度校正因子和摩阻校正因子对井底压力的贡献度不一样所导致,其中密度校正因子的贡献度较大,两者比值大约为20:1。
为了定量评价解释模型的计算精度,针对贡献度较低的摩阻校正因子开展误差统计分析,使用的统计参数有平均绝对相对误差、最大绝对相对误差、最小绝对相对误差和均方根误差。
平均绝对相对误差是反映计算结果偏离真实值的绝对相对偏差估计:
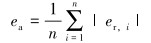
|
(25) |
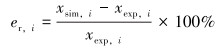
|
(26) |
最大绝对相对误差:
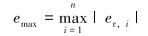
|
(27) |
最小绝对相对误差:
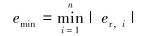
|
(28) |
均方根误差是反映一组数据的离散程度:
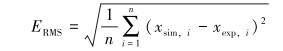
|
(29) |
不同双测点距离的误差统计分析结果如表 1所示。由表 1可知,双测点距离30 m时误差统计的各项指标明显优于双测点距离20和10 m,其平均绝对相对误差为2.87%,最大和最小绝对相对误差分别为10.02%、0.057%,均方根误差为0.036 6。但是,当双测点距离达到30 m后,随着双测点距离的继续增加,反演精度的提高很有限,同时会大大增加有线钻杆的成本,因此双测点间距不宜过大。结合工程上允许的计算误差分析[16],即平均绝对相对误差不超过5%,最大绝对相对误差不超过15%,优选合理的双测点距离为30 m,这样既可以保证较高的反演计算精度,同时还可以有效节约成本。
| 误差类型 | 双测点距离10 m | 双测点距离20 m | 双测点距离30 m |
| ea/% | 7.300 | 5.190 | 2.870 |
| emax/% | 24.370 | 18.040 | 10.020 |
| emin/% | 1.600 | 0.230 | 0.057 |
| ERMS | 0.090 0 | 0.065 2 | 0.036 6 |
4 结论
(1) 建立了结合无迹卡尔曼滤波技术与水力学模型的井下双测点压力实时解释模型。结合控压钻井工艺特点,确定了模型的反演参数为密度校正因子和摩阻校正因子,从理论上证明了双测点测量要优于单测点测量,其反演参数更加全面。
(2) 双测点压力与反演参数的计算值可以根据新获取的测量值进行实时校正,其中双测点压力校正值与测量值很接近,而反演参数的计算值在其真实值附近呈小幅上下波动。
(3) 反演参数的反演精度随着双测点距离的增加而提高,结合工程上允许的计算误差分析,优选合理的双测点距离为30 m,这样既保证了较高的反演计算精度,同时还降低了有线钻杆的使用成本。
| [1] |
HANNEGAN D, TODD R J, PRITCHARD D M, et al. MPD-uniquely applicable to methane hydrate drilling[R]. SPE 91560, 2004.
|
| [2] |
KAASA G O, ØYVIND N S, IMSLAND L, et al. Simplified hydraulics model used for intelligent estimation of downhole pressure for a managed-pressure-drilling control system[J]. SPE Drilling & Completion, 1998, 27(2): 127-138. |
| [3] |
STUNDNER M, AL-THUWAINI J S. How data-driven modeling methods like neural networks can help to integrate different types of data into reservoir management[R]. SPE 68163, 2001.
|
| [4] |
MALLARY C R, VARCO M, QUINN D. Pressure-while-drilling measurements to solve extended-reach drilling problems on Alaska's North Slope[J]. SPE Drilling & Completion, 2002, 17(2): 99-105. |
| [5] |
ROMMETVEIT R, BJøRKEVOLL K S, HALSEY G W, et al. Drilltronics: an integrated system for real-time optimization of the drilling process[R]. SPE 87124, 2004.
|
| [6] |
ROMMETVEIT R, BJøRKEVOLL K S, HALSEY G W, et al. Drilling: a system for real-time drilling simulation, 3D visualization, and control[R]. SPE 106903, 2007.
|
| [7] |
GANDELMAN R, MARTINS A L, TEIXEIRA G T, et al. A comprehensive methodology to avoid and remediate drilling problems by real time PWD data interpretation[R]. SPE 124116, 2009.
|
| [8] |
GANDELMAN R, WALDMANN A, MARTINS A L. Field implementation of a real time drilling problem diagnostic for deepwater exploratory wells[R]. OTC 20652, 2010.
|
| [9] |
LORENTZEN R J, NAEVDAL G, LAGE A C V M. Tuning of parameters in a two-phase flow model using an ensemble Kalman filter[J]. International Journal of Multiphase Flow, 2003, 29(8): 1283-1309. DOI:10.1016/S0301-9322(03)00088-0 |
| [10] |
GRAVDAL J E, LORENTZEN R J, FJELDE K K, et al. Tuning of computer model parameters in managed-pressure drilling applications using an unscented-Kalman-filter technique[J]. SPE Journal, 2010, 15(3): 856-866. DOI:10.2118/97028-PA |
| [11] |
郗凤亮, 徐朝阳, 马金山, 等. 控压钻井自动分流管汇系统设计与数值模拟研究[J]. 石油钻探技术, 2017, 45(5): 23-29. XI F L, XU C Y, MA J S, et al. Design and numerical simulation of an automatic diverter manifold in managed pressure drilling[J]. Petroleum Drilling Techniques, 2017, 45(5): 23-29. |
| [12] |
JULIER S J, UHLMANN J K. A new extension of the Kalman filter to nonlinear systems[C].Proceedings of the SPIE.[S.l.]: SPIE, 1997.
|
| [13] |
WAN E A, VAN D M R.The unscented Kalman filter for nonlinear estimation[C].Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000.[S.l.]: IEEE, 2000. https://ieeexplore.ieee.org/document/882463
|
| [14] |
REED T D, PILEHVARI A A. A new model for laminar, tansitional, and turbulent flow of drilling muds[R]. SPE 25456, 1993.
|
| [15] |
KARSTAD E. Analysis of ballooning effects during drilling of high pressure high temperature wells[R]. SPE 52066, 1998.
|
| [16] |
何淼.控压钻井溢流实时解释理论与控制方法研究[D].北京: 中国石油大学(北京), 2016. HE M. Influx real time interpretation theory and control method in managed pressure drilling[D]. Beijing: China University of Petroleum(Beijing), 2016. |



