0 引言
目前国内油田共有机械采油井近20万口,其中有杆抽油机井占比80%,在采油工程中依然占主导地位[1]。抽油机杆柱系统作为有杆抽油系统的组成部分,起着传递动力和承受井下载荷的重要作用,而抽油机井因杆柱失效而修井的次数约占总修井次数的60%[2]。杆柱失效主要由偏磨引起,包括光杆与盘根盒的偏磨、抽油杆与油管的偏磨、柱塞与泵筒的偏磨。光杆与盘根盒的偏磨会造成井口跑油、跑水,污染环境;抽油杆的偏磨会使接箍磨损严重,导致接箍处脱扣,杆柱脱落,造成巨大经济损失;柱塞与泵筒的偏磨会造成泵的漏失,磨损严重时,柱塞会偏心失效[3]。
油田现有的杆柱系统防偏磨方法是在抽油杆上安装防偏磨装置,以该装置的磨损代替抽油杆柱的磨损[4]。此方法需要运用复杂的杆柱力学并结合井下工况计算其安装位置,不能实现精确计算,导致其防偏磨效果有限。此外,此方法也不能够解决光杆以及柱塞的偏磨问题。因此,研制新型杆柱系统防偏磨装置具有重要的工程实践意义。
基于以上问题,笔者提出了“抽油机井杆柱系统防偏磨装置”的设计方案,基于CAD软件SolidWorks建模平台进行了结构设计,利用CAE动力学分析软件ADAMS并结合油井工况对其进行了仿真分析,同时对关键部件进行了优化设计。抽油机井杆柱系统防偏磨装置可以将杆柱系统的偏磨变成周向均匀磨损,从而延长修井周期,节约开采与维护成本。
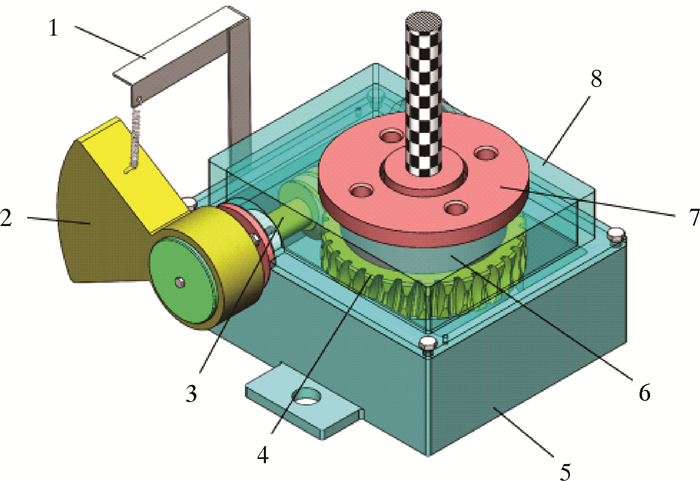
1 光杆防偏磨装置结构设计 1.1 结构抽油机井杆柱系统防偏磨装置由箱体总成、传动机构总成以及重锤总成等组成。箱体总成包括下箱体、上箱体、推力球轴承、碟形弹簧、弹簧压盖以及箱体压盖等。传动机构总成包括蜗轮、蜗杆、第一深沟球轴承组和第二深沟球轴承组以及超越离合器总成等部件。重锤总成包括重锤、弹簧、侧板和弹簧支架等。抽油机井杆柱系统防偏磨装置三维结构图如图 1所示。
|
| 1—拉力弹簧支架;2—重锤;3—蜗杆;4—蜗轮;5—下箱体;6—碟形弹簧;7—弹簧压盖;8—上箱体。 图 1 抽油机井杆柱系统防偏磨装置三维结构图 Fig.1 Three-dimensional structural schematic of the anti-eccentric device for rod string system in pumping wells |
1.2 工作原理
在上、下冲程过程中,悬点加速度服从三角函数分布,即在每个冲程中,悬点加速度都有方向向上和方向向下两个阶段。
上冲程第一阶段,从下死点到冲程中点,这一段悬点加速度方向向上。重锤受重力和弹簧拉力,相对于悬点加速度产生一个向下的力。在下死点位置时,重锤重力与弹簧弹力平衡,重锤不动;当装置随悬点向上运动时,重锤受力为重力与加速度产生的力之和,重锤向下摆动,弹簧继续拉长直至弹簧拉力与重锤受到向下的力相平衡,此时重锤位于装置最下端。
上冲程第二阶段,从冲程中点到上死点,这一段悬点加速度方向向下。装置向上运动,重锤受重力和弹簧拉力,相对于悬点加速度产生一个向上的力。此时弹簧拉力与加速度产生的力之和大于重力,重锤会受到一个向上的合力,合力克服阻力矩做功,向上摆动,直至重锤合力提供的力矩小于阻力矩做功,重锤回落到下端。
下冲程第一阶段,从上死点到冲程中点,这一段悬点加速度方向向下。重锤受重力和弹簧拉力,相对于悬点加速度产生一个向上的力。在上死点位置时,重锤处于装置最下端;当装置随悬点向下运动时,重锤受到的弹簧拉力与加速度产生的力之和大于重力,重锤会受到一个向上的合力,合力克服阻力矩做功,向上摆动,直至重锤合力提供的力矩小于阻力矩做功,重锤回落到装置下端。
下冲程第二阶段,从冲程中点到下死点,这一段悬点加速度方向向上。重锤受重力和弹簧拉力,相对于悬点加速度产生一个向下的力。在下死点位置时,重锤重力与弹簧弹力平衡,重锤不动;当装置随悬点向上运动,重锤受到的重力与加速度产生的力之和大于弹簧拉力,重锤向下摆动,弹簧继续拉长直至弹簧拉力与重锤受到向下的力相平衡,此时重锤位于装置最下端。
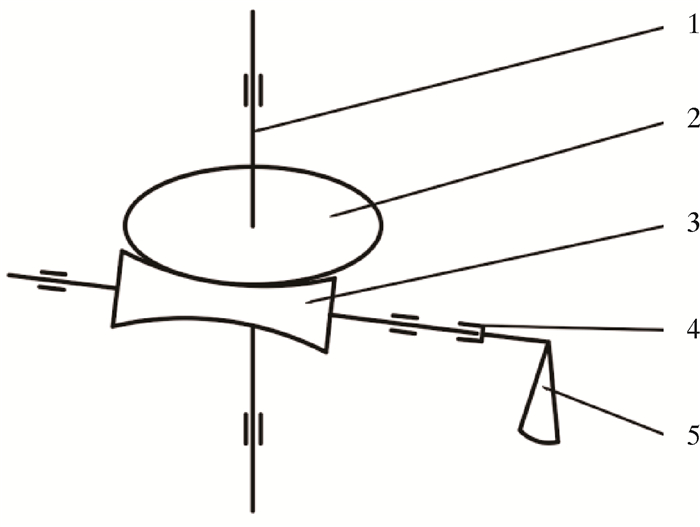
整个运动过程由于超越离合器的作用,重锤只有自下而上摆动时,重锤才能带动蜗杆转动。抽油机井杆柱系统防偏磨装置工作原理简图如图 2所示。
|
| 1—光杆;2—蜗轮;3—蜗杆;4—超越离合器;5—重锤。 图 2 抽油机井杆柱系统防偏磨装置原理简图 Fig.2 Schematic diagram of the anti-eccentric device for rod string system in pumping wells |
装置输出的动力具有间歇性,输出的能量存储为抽油杆的扭转弹性变形能,在抽油杆上下行程过程中有效地传下去,一方面可以避免或减少抽油杆与油管壁的偏磨,另一方面还可以防止脱扣和松扣现象的发生。另外,由于本装置的输出转速很低,带动杆柱系统旋转角度很小且是间歇旋转,所以装置的工作稳定性比较好,不会因转速过大带来的巨大摩擦而导致装置失效。
2 抽油机井杆柱系统扭转力矩及重锤旋转角度的计算使抽油杆旋转需要克服的摩擦阻力矩有抽油杆与井内液体之间的摩擦阻力矩M1、抽油杆下部滚动轴承的摩擦阻力矩M2、抽油泵柱塞与泵筒之间的摩擦阻力矩M3以及抽油杆接头与油管之间的摩擦阻力矩M4。
由于抽油杆转速非常低,故其与井内液体之间的摩擦阻力矩很小,可忽略不计。
抽油杆下部滚动轴承的摩擦阻力矩M2计算公式为:
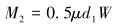
|
(1) |
式中:d1为轴承内径;μ为轴承摩擦阻力因数,取0.001;W为轴承承受的最大轴向载荷,即油管柱重力和液柱重力。
抽油泵柱塞与泵筒之间的摩擦阻力矩M3计算公式为:
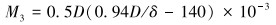
|
(2) |
式中:D为泵筒内径;δ为在柱塞衬套副半径上的间隙,取0.1 mm。
M4时大时小,这个力矩的大小主要取决于抽油杆弯曲变形的程度,但这两个量及井斜的程度很难定量描述。考虑到抽油杆旋转系统的通用性,引入杆管接触程度影响系数K1=4,则抽油杆接头与油管之间的摩擦阻力矩M4计算公式为:
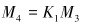
|
(3) |
转动抽油杆所需克服的总摩擦阻力矩Mz计算公式为:
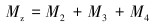
|
(4) |
若要使抽油杆转动,则重锤应提供的力矩Mc计算公式为:
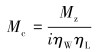
|
(5) |
式中:Mz为抽油杆转动需要在蜗轮上加的驱动力矩;ηW为蜗轮蜗杆传动效率,取ηW=0.75;ηL为超越离合器传动效率,取ηL=0.7;i为传动比。
抽油机运动时,曲柄的角速度ω计算公式为:
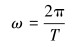
|
(6) |
式中:T为周期。
悬点加速度a计算公式为:
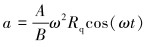
|
(7) |
式中:A为游梁的前臂长度;B为游梁的后臂长度;Rq为曲柄半径;t为时间。
当重锤向上摆动时,重锤带动蜗轮蜗杆转动所需的加速度a1计算公式为:
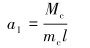
|
(8) |
式中:mc为重锤质量;l为摆动位移,取l=0.2 m。
由重锤的运动特性可知,重锤摆动角度α计算公式为:
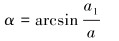
|
(9) |
经计算,转动抽油杆所需克服的总摩擦阻力矩Mz为9 199 N·mm,重锤应提供的力矩Mc为565 N·mm,重锤在上冲程第二阶段和下冲程第一阶段的摆动角度和为30°,蜗轮转动角度为0.968°。
3 虚拟样机建立及仿真 3.1 建立仿真模型ADAMS软件具有很强的机械系统运动分析仿真功能,但实体建模能力较弱,而三维设计软件如SolidWorks具有强大的建模功能。因此,笔者结合两者优点,先在Solidworks软件中进行抽油机光杆防偏磨装置的建模,再将建好的模型保存成parasolid(*.x_t)格式[5],进入ADAMS界面后将装置各部分依次导入,完成模型创建。
根据抽油机光杆防偏磨装置的实际工作情况,将其各个机构用相应的旋转副和移动副等连接起来,并定义重力加速度大小和各部件的材料属性。
3.2 选取ADAMS动力碰撞参数在蜗轮与蜗杆之间定义动力碰撞接触力,可以使虚拟样机模型更加符合物理样机模型。本文采用Impact法[6],其函数定义为:

|
(10) |
式中:STEP是阶跃函数,q0是两物体之间的初始距离,q是两物体发生碰撞过程中的实际距离,q0-q表示碰撞过程中的变形量,e为碰撞指数,c为阻尼系数,d为变形距离。
当q≥q0时,两物体不发生碰撞,即F_Impact=0;当q < q0时,两物体发生碰撞,碰撞力的大小与刚度系数K、变形量q0-q、碰撞指数e、阻尼系数c和阻尼完全作用时变形距离d有关[7-8]。
刚度系数K取决于两物体的材料和结构,根据Hertz碰撞理论[9-10],可由下式计算得到:
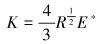
|
(11) |
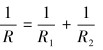
|
(12) |
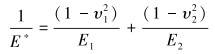
|
(13) |
式中:R为接触点的当量曲率半径;R1和R2分别是蜗轮蜗杆接触点的当量半径;E1和E2分别是蜗轮和蜗杆材料的弹性模量,E1=105 GPa,E2=209 GPa;υ1和υ2分别是蜗轮和蜗杆的材料泊松比,υ1=0.25,υ2=0.27。
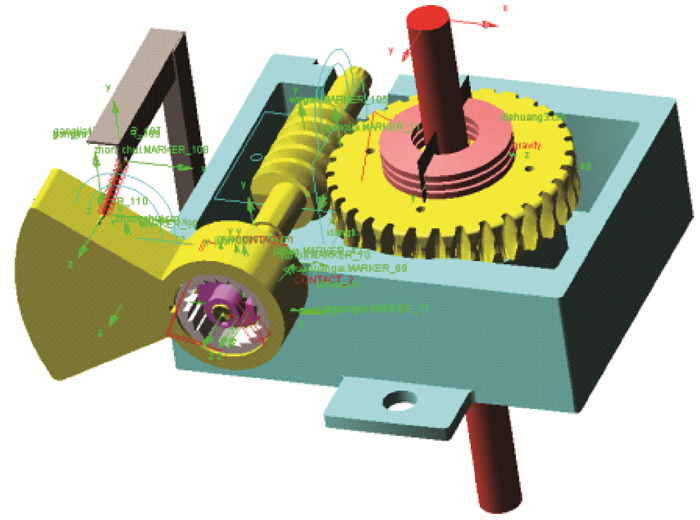
根据式(11)可得蜗轮蜗杆碰撞刚度系数为K=652 N/mm。对蜗轮和蜗杆之间进行脂润滑处理,动摩擦因数取0.05,静摩擦因数取0.08。虚拟样机模型如图 3所示。
|
| 图 3 虚拟样机模型 Fig.3 Virtual prototype model |
3.3 仿真结果分析
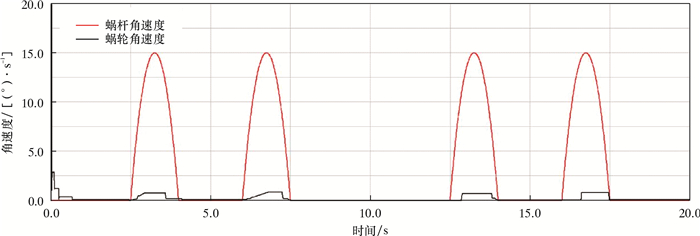
根据抽油机悬点运动规律,在箱体移动副上施加移动驱动,并在抽油杆柱上添加已计算出的静态载荷T=9 199 N·mm,得到蜗轮蜗杆的转速曲线如图 4所示,重锤转矩如图 5所示。
|
| 图 4 蜗轮蜗杆转速曲线 Fig.4 RPM of the worm and gear |
|
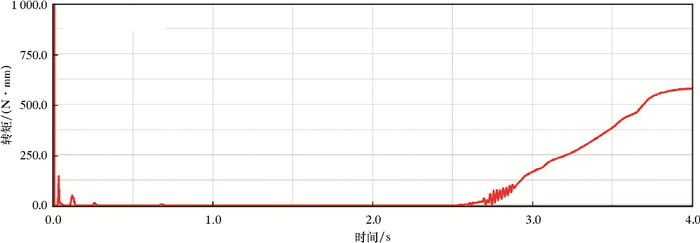
| 图 5 重锤转矩曲线 Fig.5 Heavy hammer torque curve |
从图 4可以看到,蜗轮转速在刚开始仿真时出现了小幅度的波动,这是因为蜗轮蜗杆在建模(初始)时未处于平衡位置,之后蜗轮自行调整恢复角速度为零的初始状态。在运动仿真的过程中,蜗杆转速呈周期性变化,转速平均值稳定在9.95 (°)/s,蜗轮转速平均值稳定在0.327 (°)/s,由传动比i=31可知,蜗轮的理论转速为0.322 (°)/s。仿真值与理论值相对误差为1.52%。从图 5可以看到,重锤转矩的最大值为576.95 N·mm,与理论值565 N·mm的相对误差为2.00%,验证了虚拟样机的正确性。
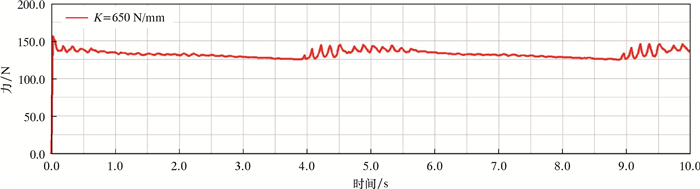
图 6为蜗轮蜗杆啮合力曲线。由图 6可知:在0.00~0.18 s内啮合力没有变化,说明此时蜗轮蜗杆尚未接触;当蜗轮蜗杆开始接触时,啮合力瞬间达到77.3 N;随后,蜗轮在蜗杆的驱动下开始啮合,啮合力迅速稳定在132 N左右,这是材料本身的惯性作用导致的滞后现象。之后蜗轮蜗杆在传动过程中的啮合力随着加载的稳定逐渐趋于稳定均值的状态并伴随着小幅度的波动,其中出现的波动主要是蜗轮蜗杆啮合过程中产生的碰撞引起的。从图 6可以发现,蜗轮蜗杆啮合过程中的碰撞冲击是周期性的,这种周期性的波动容易造成蜗轮蜗杆传动机构的疲劳破坏,也会破坏齿轮的承载平稳性,降低齿轮传动效率,最终导致其工作寿命缩短。因此,降低啮合力的波动幅值和缩短波动时长可以有效地延长蜗杆传动机构的工作寿命并提高其工作精度。
|
| 图 6 蜗轮蜗杆啮合力曲线 Fig.6 Meshing force of the worm and gear |
3.3.1 刚度系数对啮合力的影响
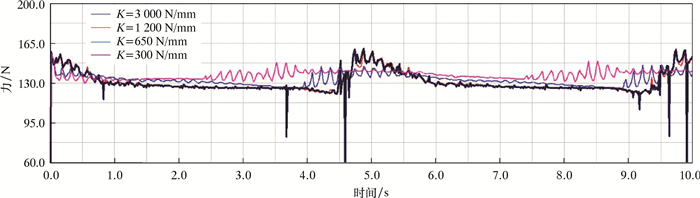
为了研究刚度系数对蜗杆传动机构啮合力的影响,在输入速度和外载荷等都相同的情况下,分别取刚度系数300、650、1 200和3 000 N/mm。其仿真结果如图 7所示。
|
| 图 7 不同刚度系数下蜗轮蜗杆啮合力变化曲线 Fig.7 Variation of worm and gear meshing force under different stiffness coefficients |
从图 7可以看出:当K=300 N/mm时,啮合力均值为137.150 N,最大值为156.125 N;当K=650 N/mm时,啮合力均值为132.830 N,最大值为158.237 N;当K=1 200 N/mm时,啮合力均值为131.090 N,最大值为159.805 N;当K=3 000 N/mm时,啮合力均值为130.240 N,最大值为160.237 N。当刚度系数为300、650和1 200 N/mm时,啮合过程中没有发生力的突变,说明蜗轮蜗杆传动良好,无较大碰撞冲击。当刚度系数为3 000 N/mm时曲线出现了尖点,说明啮合过程中发生了较大的碰撞冲击。由以上数据可以得出以下结论:
(1) 在不同刚度系数下,蜗轮蜗杆啮合力都呈周期性变化,不会发生啮合力的周期紊乱现象;
(2) 蜗轮蜗杆传动机构有其适用的刚度系数范围,刚度系数过大会导致啮合出现较大冲击;
(3) 随着刚度系数的增大,蜗轮蜗杆传动机构啮合力均值逐渐下降,波动幅度逐渐加大,波动时长逐渐缩短。
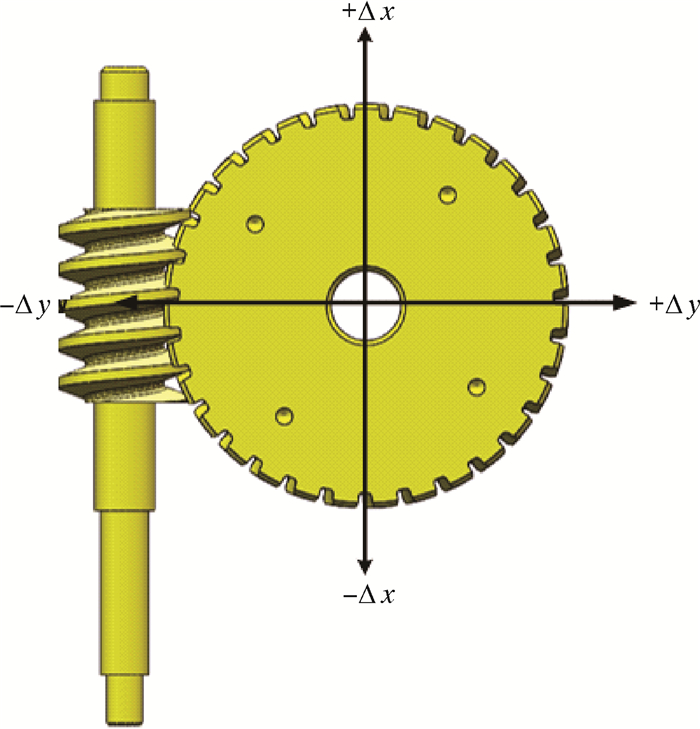
3.3.2 安装误差对啮合力的影响由于蜗轮蜗杆安装时不可能出现彼此嵌入的情形,所以在虚拟装配时出现面干涉时,就要特别注意负值的选定不能过大。为了研究安装误差对啮合力的影响,在输入速度和外载荷相同的情况下,设定刚度为上文已得出的较为合适的刚度650 N/mm,对其不同径向位移误差和切向位移误差进行仿真研究。安装误差方向的选择如图 8所示。图 8中Δx表示蜗轮的径向位移误差,Δy表示蜗轮的切向位移误差。
|
| 图 8 安装误差径向和切向方向示意图 Fig.8 Schematic diagram of installation error at radial and tangential directions |
Δx与Δy对蜗轮蜗杆的切向啮合力和轴向啮合力影响不明显,对蜗轮蜗杆的径向啮合力影响较为明显。
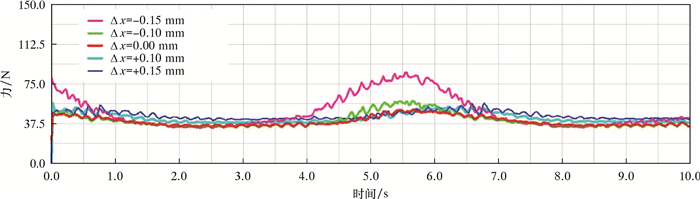
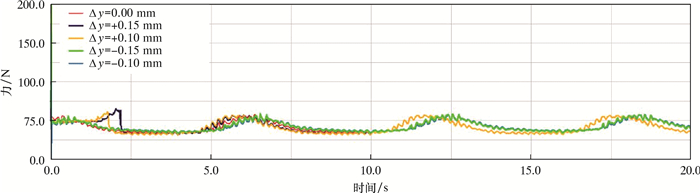
仿真得到安装误差Δx影响下径向啮合力曲线如图 9所示,安装误差Δy影响下径向啮合力曲线如图 10所示。
|
| 图 9 不同径向位移安装误差下蜗轮蜗杆径向啮合力变化曲线 Fig.9 Radial meshing force of the worm and gear under different radial displacement installation errors |
|
| 图 10 不同切向位移安装误差下蜗轮蜗杆径向啮合力变化曲线 Fig.10 Radial meshing force of the worm and gear under different tangential displacement installation errors |
从图 9可以看出:Δx为0.00 mm时,径向啮合力均值为39.68 N,最大值为50.74 N;Δx为0.10 mm时,径向啮合力均值为42.90 N,最大值为56.70 N;Δx为0.15 mm时,径向啮合力均值为45.16 N,最大值为56.93 N;Δx为-0.10 mm时,径向啮合力均值为40.31 N,最大值为59.19 N;Δx为-0.15 mm时,径向啮合力均值为48.13 N,最大值为58.91 N。当径向位移误差正向增大时,啮合力呈上升趋势,增加较为平缓,波动幅度变化不大;当径向位移误差反向增大时,啮合力快速上升,波动幅度较大。由此可见,在安装存在径向位移误差的情况下,曲线波动非常不平稳,随着径向位移误差的不断变大,蜗轮蜗杆径向啮合力曲线波动加强。
从图 10可以看出:Δy为0.00 mm时,径向啮合力均值为39.68 N,最大值为50.74 N;Δy为0.10 mm时,径向啮合力均值为41.62 N,最大值为61.63 N;Δy为0.15 mm时,径向啮合力均值为41.61 N,最大值为111.47 N;Δy为-0.10 mm时,径向啮合力均值为42.53 N,最大值为58.18 N;Δy为-0.15 mm时,径向啮合力均值为42.87 N,最大值为215.37 N。当切向位移误差在0.10 mm时,啮合力小幅增加,接触前期出现不规律波动,之后曲线与啮合良好的曲线波形基本一致;当切向位移误差在-0.10 mm时,径向啮合力均值也变动不大,但其波动延迟出现;当切向位移误差的绝对值大于0.10 mm时,蜗轮蜗杆接触瞬间啮合力急剧上升,说明蜗轮蜗杆发生强烈碰撞。
由以上数据可知,蜗轮蜗杆的径向位移误差控制在±0.10 mm较为合理,蜗轮蜗杆的切向位移误差控制在0.00~0.10 mm较为合理,这时蜗轮蜗杆的啮合力受影响较小,啮合曲线波形与正常波形基本一致,波动幅度变化不大。因此,蜗轮蜗杆安装允许存在一定的误差范围,但是又必须严格控制安装误差。
4 结论(1) 通过对抽油机井杆柱系统防偏磨装置的建模和仿真,得到了重锤的转矩曲线和蜗轮蜗杆啮合力变化曲线,为其性能优化提供了参考依据。
(2) 利用重锤的摆动产生动力,无需外加动力源,合理利用了能量,同时简化了机械结构,增强了装置的可靠性。
(3) 装置每个冲程带动杆柱系统转动0.968°,杆柱系统转动缓慢均匀。装置使杆柱系统的偏磨变成了周向均匀磨损,延长了修井周期,降低了采油成本。
(4) 在蜗轮蜗杆适用的刚度系数范围内,随着刚度系数的增加,蜗轮蜗杆传动机构啮合力均值逐渐下降,波动幅度逐渐加大,波动时长逐渐缩短。
(5) 蜗轮蜗杆的径向位移误差控制在±0.1 mm,蜗轮蜗杆的切向位移误差控制在0.00~0.10 mm较为合理,此时蜗轮蜗杆的啮合力受影响较小,啮合曲线波形与正常波形基本一致,波动幅度变化不大。
| [1] |
杨海滨. 抽油井杆管防偏磨理论研究与技术实践[M]. 北京: 中国石化出版社, 2012: 27-31. YANG H B. Theoretical research and technical practice on anti-eccentric wear of sucker rod and tubing in pumping wells[M]. Beijing: China Petrochemical Press, 2012: 27-31. |
| [2] |
陈斌.抽油杆旋转抗磨减载装置: 200520030187.6[P].2006-07-05. CHEN B. Rotary Anti-wear and load reduction device for sucker rod: 200520030187.6[P].2006-07-05. |
| [3] |
张新强, 齐长智, 李继原. 抽油井偏磨的原因及防治对策[J]. 内蒙古石油化工, 2006(5): 194-195. ZHANG X Q, QI C Z, LI J Y. Causes of eccentric wear in pumping wells and preventive measures[J]. Inner Mongolia Petrochemical Industry, 2006(5): 194-195. DOI:10.3969/j.issn.1006-7981.2006.05.113 |
| [4] |
贾德有. 油井杆管偏磨原因分析及防治方法研究[J]. 内蒙古石油化工, 2011(10): 21-22. JIA D Y. Cause analysis and prevention method of eccentric wear of rod and tube in oil well[J]. Inner Mongolia Petrochemical Industry, 2011(10): 21-22. DOI:10.3969/j.issn.1006-7981.2011.10.008 |
| [5] |
余波, 王家序, 黄春美, 等. 基于ADAMS的孔销式少齿行星减速器的设计与仿真分析[J]. 机械设计与研究, 2013, 29(3): 23-27. YU B, WANG J X, HUANG C M, et al. The design and simulation analysis of hole-pin type few teeth difference planet-gear speed reducer based on ADAMS[J]. Machine Design & Research, 2013, 29(3): 23-27. DOI:10.3969/j.issn.1006-2343.2013.03.006 |
| [6] |
李新华, 刘洋, 陈泽宇. 汽车座椅电机蜗轮蜗杆传动机构的仿真分析[J]. 制造业自动化, 2014(5): 81-83. LI X H, LIU Y, CHEN Z Y. The simulation analysis of automotive seat motor's worm wheel transmission mechanism[J]. Manufacturing Automation, 2014(5): 81-83. |
| [7] |
李长群, 贾长治, 武彩岗. 基于虚拟样机技术的齿轮啮合力动力学仿真研究[J]. 系统仿真学报, 2007, 19(4): 203-206. LI C Q, JIA C Z, WU C G. Dynamic simulation study of gear meshing based on virtual prototyping technology[J]. Journal of System Simulation, 2007, 19(4): 203-206. |
| [8] |
龙凯, 程颖. 齿轮啮合力仿真计算的参数选取研究[J]. 计算机仿真, 2002, 19(6): 87-88. LONG K, CHENG Y. The research of parameters by the simulation of exciting force in gears[J]. Computer Simulation, 2002, 19(6): 87-88. DOI:10.3969/j.issn.1006-9348.2002.06.028 |
| [9] |
HUANG Z P, MA J S, WU D L. Simulation study on contact stress of gear tooth[J]. Journal of Mechanical Transmission, 2007, 31(2): 26-28. |
| [10] |
王雁. 基于ADAMS的变速箱齿轮的运动学和动力学仿真[J]. 制造业自动化, 2011(5): 111-112. WANG Y. Kinematics and dynamics simulation of transmission gear based on ADAMS[J]. Manufacturing Automation, 2011(5): 111-112. DOI:10.3969/j.issn.1009-0134.2011.3a.39 |



