2. 中海油深圳分公司
2. CNOOC Shenzhen Company
0 引言
随着全球油气总量的不断降低以及人们勘探钻采技术水平的提高,海洋油气田开发不断从浅水向深水区域迈进,深水环境下海洋油田开发技术是石油行业的主要革新点[1],张力腿平台(Tension Leg Platform, TLP)以其优良的性能和较强的抗恶劣环境能力等优点被广泛应用于深水油气田开发[2-3]。在TLP平台所采用的顶张紧式立管系统中,将底部弯曲的抑制结构称为锥形应力节(TSJ)。TSJ在作业过程中主要承受来自立管的轴向应力和弯矩作用,通过改变自身壁厚来抑制立管系统底部结构的弯曲应力集中程度,减轻立管系统底部弯矩对井口的作用,这种特殊作业装备往往是容易导致系统损伤失效的关键所在[4-5]。在实际钻井过程中,由于水下井口不太可能绝对垂直下入,于是当回接连接器与井口对接后导致TSJ处于倾斜状态。为此,开展实际作业工况下的锥形应力节结构强度及其可靠性研究,并提出相应的可靠性设计准则,对于立管系统结构设计和作业安全具有重要意义。
结构可靠性研究从20世纪50年代发展起来,1947年A.M. FREUDENTHAL[6]提出将应力-强度干涉模型用于研究结构的应力强度。D.KARUNAKARAN等[7]首次将可靠性分析方法应用到极限状态下的立管系统中,极限状态函数的求解采用一阶二次矩法、二阶二次矩法和响应面法。B.J.LERIA等[8]开展了不同作业工况下深水立管结构研究,包括生产、钻完井和修井3种工况,并对立管断裂和可靠性方面的研究现状进行总结。戴伟[9]采用响应面法对立管极限风暴载荷下和涡激振动下的可靠性进行了研究,并与Monte-Carlo法的计算结果进行了对比。V.BAUGUS等[10]针对计算载荷情况下的锥形应力节参数进行研究,根据应力节的优点制定了选择设计参数的基本原则。N.CUNLIFFE等[11]在锥形应力节满足设计要求的情况下对其进行了设计优化。L.C.M.MENICONI等[12]分析计算得到了锥形应力节轴向力和弯矩沿长度方向的变化规律,并确定了应力节壁厚的选择原则。郑文青等[13]针对锥形应力节这种承受复杂海洋环境载荷和腐蚀下的结构提出了多轴疲劳分析理论,研究结果表明,多轴疲劳分析能够准确地反映结构的疲劳状态。张日曦[14]提出了锥形应力节的设计理论,并进行了验证。尽管上述文献在锥形应力节的结构强度与设计方面开展了大量研究,但是关于不同随机变量对锥形应力节强度可靠性的影响研究仍处于空白。
笔者提出一种基于Kriging模型的可靠度计算方法,以深水TLP平台立管系统中的锥形应力节在实际作业工况下的响应为基础,考虑环境因素、作业因素及结构因素的随机性,以海流、张力比、材料及尺寸参数作为随机变量,建立不同井口倾斜角度下锥形应力节的极限状态方程,分析井口倾斜角度与锥形应力节强度及可靠性之间的关系,研究环境及作业参数对可靠度计算结果的影响,并最终形成锥形应力节强度可靠性设计准则。研究结果可为TLP特殊钻完井作业装备的设计和安全作业提供技术支持和保障。
1 基于Kriging模型的锥形应力节可靠性分析方法 1.1 Kriging模型简介Kriging法是一种半参数化的模拟方法,所需参数少、计算量小,而且模型简单,通过少量样本试验即可确定估计模型。这种方法可以最大程度地利用现有的有限元分析软件,提高了计算效率,保证了可靠度结果的精度。S.LOPHAVEN和H.NIELSEN等基于Matlab数学计算软件编写了用于建立、估计及预测Kriging模型的DACE工具箱,大大提高了Kriging模型的使用效率。Kriging作为一种改进的线性回归分析技术,包括线性回归部分和非参数部分[15],其中非参数部分用来表现参数的随机分布特征。常采用的Kriging模型形式为[16]:
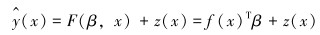
|
(1) |
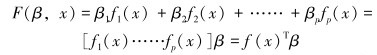
|
(2) |
式中:β为线性回归系数;f(x)为变量X的多项式函数,其具体形式可为多项式函数或固定常数;z(x)用来模拟局部近似,即y(x)的局部变化。
DACE工具箱包含3种回归模型[17]。
(1) 常数,P=1:
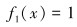
|
(3) |
(2) 线性,P=n+1:
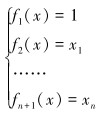
|
(4) |
(3) 二次,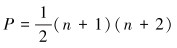
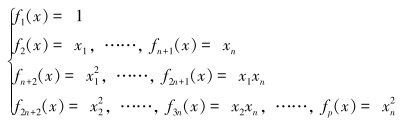
|
(5) |
常数形式的回归模型适用于非线性程度不高的结构,但是对于非线性程度较高的结构,应采用线性或者二次形式的回归模型。文中计算柔性管系统和锥形应力节这类复杂结构时,采用线性函数作为回归函数模型。
建立Kriging模型后,可以通过试验设计法选取取样点来验证模型的精度,以确保后期可靠度计算的准确性。笔者选择高斯函数作为核函数,为保证模型的精确度,需要对参数θ进行优化[18]。一般通过优化问题来求解θ,笔者利用极大拟然估计法。
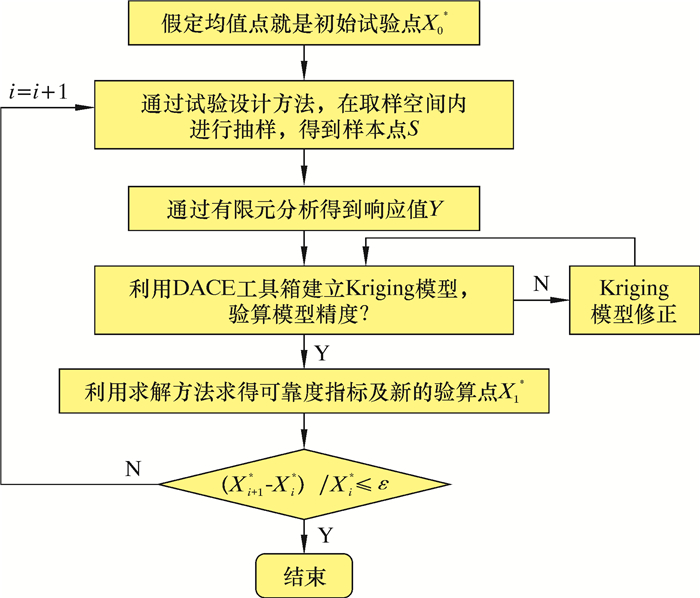
1.2 基于Kriging模型的可靠度计算流程笔者提出一种通过建立Kriging模型与拉丁超立方抽样技术相结合的可靠性分析方法,利用Kriging模型模拟精度及拉丁超立方抽样技术在抽样效率上的优势,确定了一种针对隐式功能函数的高效高精度计算方法。该方法通过试验设计得到一系列的输入随机变量,对输入参数进行确定性分析,包括有限元分析和试验分析,进而可得到相对应的输出。然后采用MATLAB软件DACE工具箱中的dacefit函数建立Kriging模型,并对其中关键参数θ进行优化,得到输入与输出的关系。通过predictor函数可对已建立的Kriging模型进行待测点预测,验证模型的精度是否满足可靠度计算要求。具体流程如图 1所示。
|
| 图 1 基于Kriging模型的可靠性分析流程 Fig.1 Reliability analysis procedure based on Kriging model |
2 井口倾斜下锥形应力节的局部响应分析 2.1 局部分析模型
TLP平台深水作业通常采用的是喷射钻井的作业方式,喷射下入过程中不可避免地会出现导管不是完全垂直下入的现象。导管的倾斜势必会导致井口及井口回接装置的倾斜,立管与锥形应力节连接处受到井口回接装置倾斜和顶部张紧力的影响[19],会产生一定的弯曲,连接处即为俗称的“狗腿”位置。在“狗腿”位置往往会出现较为复杂的应力情况,根据钻井作业标准,在现场实际作业过程中通常设置井口倾斜角度的预警值为1.5°。
依据圣维南原理,为保证模型的计算精度,全面考虑边界条件的影响,锥形应力节模型主体由锥形应力节部分及附带考虑的一段立管这两部分构成。采用ABAQUS有限元仿真软件建立锥形应力节的局部有限元分析模型,锥形应力节和附带立管采用实体单元进行模拟,模型整体用规则的六面体网格进行划分。由于锥形应力节与立管连接处的截面尺寸发生突变,假定此处为应力突变的位置,对连接处的网格进行细化,以提高求解精度。划分的有限元分析模型如图 2所示。在边界条件的设定方面,根据井口倾斜角度的不同将模型绕x轴进行旋转。在施加轴向力和弯矩之前,在模型顶端即附带立管顶部施加z方向的位移作为位移边界条件,并以此作为一个分析步。该分析步用来模拟模型在实际结构中立管系统受到顶部张紧力后拉回竖直方向的过程。模型下端与井口回接装置相连,可视为固定端,模型顶部立管承受轴向载荷。

|
| 图 2 锥形应力节有限元分析模型 Fig.2 Finite element analysis model of tapered stress joint |
2.2 基本参数
以南海某海域为目标油田,水深340 m。生产立管系统配置见表 1。
| 部件名称 | 数量/个 | 长度/m | 湿重/N |
| 采油树 | 1 | 2.4 | 46 744.4 |
| 张力短节 | 1 | 16.2 | 1 476.0 |
| 生产立管 | 20 | 17.1 | 804.2 |
| 锥形应力短节 | 1 | 13.4 | 4 672.5 |
| 回接连接器 | 1 | 0.9 | 12 240.9 |
| 井口 | 1 | 2.7 | 23 118.9 |
生产立管外径为273.05 mm,壁厚为10 mm,生产立管内压为3.579 MPa。本次分析中,进行100 a一遇海况下立管系统力学特性分析。张紧器正常工作时生产立管张力比(张力比=顶张力/湿重)为2.3,平台偏移为30 m。
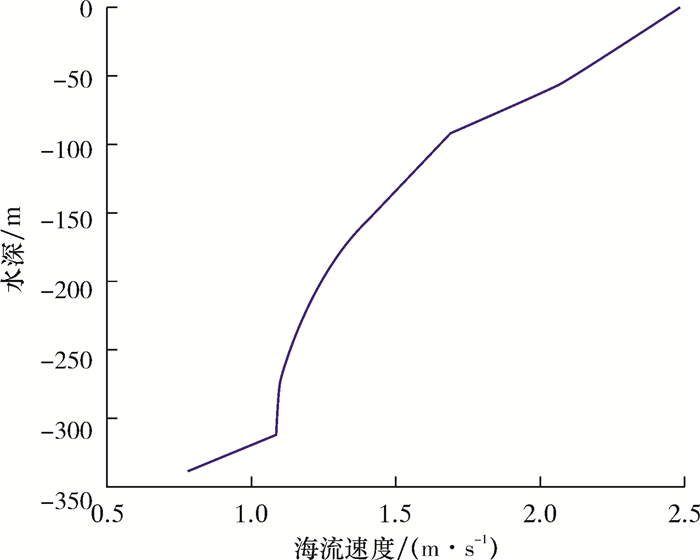
台风100 a一遇海况下流剖面如图 3所示。
|
| 图 3 台风100 a一遇下流剖面 Fig.3 Flow profile under the 100-year typhoon |
锥形应力节基本数据为附带立管长度5 m,外径273.05 mm,内径253.00 mm,锥形应力节长度13.4 mm,顶端外径273.05 mm,底端外径344.00 mm,内径253.00 mm。
2.3 不同井口倾斜角度下锥形应力节的响应由于井口倾斜角度对施加在锥形应力节模型顶端的位移和载荷都有较大的影响,所以分别建立100 a一遇井口倾斜1.2°、1.3°、1.4°、1.5°和1.6°工况下的张力腿平台TTR立管系统整体分析模型,提取立管整体分析中模型顶部位置的轴向应力和弯矩施加到锥形应力节分析模型中,作为局部分析的边界载荷。以井口倾斜1.5°为例,施加顶部位移后的锥形应力节应力云图如图 4所示。继续施加边界载荷后锥形应力节应力云图如图 5所示。

|
| 图 4 井口倾斜1.5°时顶部张紧后锥形应力节应力云图 Fig.4 Stress distribution of the tapered stress joint after top tensioning when the wellhead is inclined by 1.5° |
|
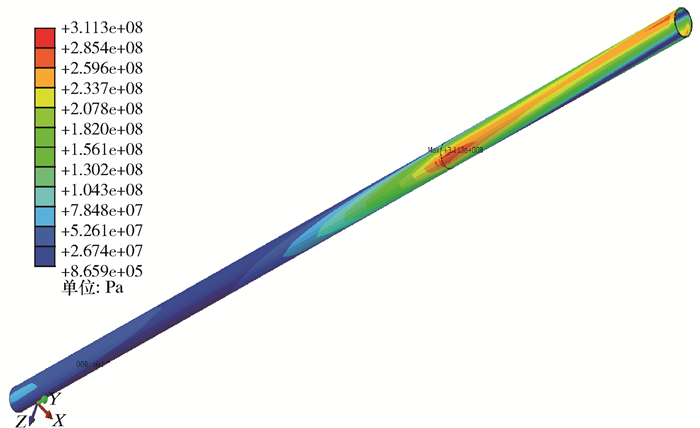
| 图 5 井口倾斜1.5°时锥形应力节应力云图(施加边界载荷) Fig.5 Stress distribution of the tapered stress joint when the wellhead is inclined by 1.5° (applying boundary loads) |
由图 4和图 5可以看出:模型中附带立管与锥形应力节接触的位置发生了明显的应力集中现象,在施加顶端位移后最大等效应力约为277.7 MPa;继续施加边界载荷后,模型最大等效应力增大,约为311.3 MPa,应力集中现象更加明显。其中锥形应力节部分的应力整体小于附带立管部分,同时由于受到轴向张力、弯矩及顶端位移的影响,导致模型应力分布不规律。
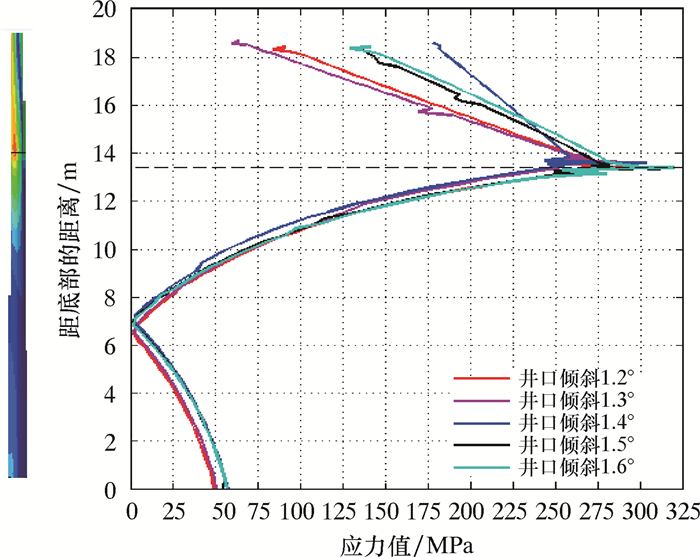
不同倾斜角度下锥形应力节沿长度方向的应力分布情况如图 6所示,具体分析结果如表 2所示。
|
| 图 6 不同倾斜角度下锥形应力节沿长度方向应力分布曲线 Fig.6 Stress distribution curve along the tapered stress joint at different inclination angles |
| 井口倾斜角/(°) | 顶端位移/m | 附带立管处载荷 | 顶端位移造成的集中应力/MPa | 危险位置最大应力/MPa | |
| 轴向力/MN | 扭矩/(N·m) | ||||
| 1.2 | 0.104 7 | 1.609 | 140 319 | 265.4 | 294.1 |
| 1.3 | 0.113 5 | 1.693 | 141 547 | 269.3 | 297.2 |
| 1.4 | 0.122 2 | 1.751 | 143 018 | 273.6 | 303.3 |
| 1.5 | 0.130 9 | 1.877 | 144 457 | 277.7 | 311.3 |
| 1.6 | 0.139 7 | 1.901 | 146 011 | 281.8 | 319.4 |
由图 6可以看出,在不同倾斜角度下锥形应力节整体应力变化规律基本相同,都在锥形应力节和附带立管接触位置发生明显的应力突变。由表 2可知,随着井口倾斜角度的增大,锥形应力节模型危险位置处的最大应力不断增大。根据笔者的计算结果,在井口倾斜1.2°时最大应力为294.1 MPa,1.6°时为319.4 MPa。这说明井口的倾斜角度对锥形应力节和立管连接位置造成较大的影响,需要对井口倾斜工况进行更深层次的分析和讨论。
3 锥形应力节结构可靠性影响因素分析 3.1 极限状态方程的建立本章以第2章所采用的基本参数作为计算数据。由于井口倾斜角不断增大,导致锥形应力节危险位置处的应力集中现象越来越明显,所以准确和科学地研究不同井口倾斜角度下结构的承载能力对其可靠性分析具有重要意义。锥形应力节在结构尺寸、材料属性、作业参数以及所处海洋环境载荷方面具有随机性,应首先确定各随机变量的概率特性。笔者考虑的随机参数包括环境参数(海流v)、作业参数(张力比)、结构参数(材料最小屈服强度)、直径d及长度l。各随机变量的概率分布特性见表 3[20-21]。
| 项目 | 张力比 | 海流 | 屈服强度 | 直径 | 长度 |
| 分布特性 | 正态 | 威布尔 | 对数正态 | 正态 | 正态 |
| 变异系数/% | 0.1 | 10.0 | 8.0 | 0.1 | 0.1 |
根据屈服强度,建立应力节的极限状态方程:
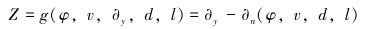
|
(6) |
式中:∂y为屈服强度,φ为张力比,∂n为通过仿真软件进行应力节结构响应分析后得到的最大应力。
3.2 不同井口倾斜角度下的锥形应力节可靠性分析在确定随机变量概率分布特性的基础上,以各随机参数均值(张力比均值2.3,海流均值2.49 m/s,屈服强度均值552 MPa,直径均值0.344 m,长度均值13.4 m)为初始采样点,利用拉丁超立方抽样技术,依据3σ准则抽取50个采样点[22]。以随机变量的向量组合作为自变量Xi(i=1, 2, ……, 50),将求得的Z(xi)(i=1, 2, ……, 50)作为相应的变量,组成一一对应的关系,进行Kriging模型拟合。分别计算不考虑环境和作业因素、考虑环境和作业因素、不考虑环境因素、不考虑作业因素4种情况下的可靠度指标,计算结果见表 4。
| 序号 | 类别 | 井口倾斜角/(°) | 可靠度指标 | 失效概率 |
| 0.0 | 4.137 9 | 1.752 5×10-5 | ||
| 1.2 | 3.912 1 | 4.574 8×10-5 | ||
| 1 | 不考虑环境和作业因素 | 1.3 | 3.809 4 | 6.965 2×10-5 |
| 1.4 | 3.737 7 | 9.285 5×10-5 | ||
| 1.5 | 3.645 1 | 1.336 4×10-4 | ||
| 1.6 | 3.501 1 | 2.316 7×10-4 | ||
| 0.0 | 3.081 9 | 0.001 028 | ||
| 1.2 | 2.906 7 | 0.001 826 | ||
| 2 | 考虑环境和作业因素 | 1.3 | 2.799 9 | 0.002 556 |
| 1.4 | 2.711 4 | 0.003 350 | ||
| 1.5 | 2.656 9 | 0.003 943 | ||
| 1.6 | 2.600 4 | 0.004 735 | ||
| 0.0 | 3.891 1 | 4.989 5×10-5 | ||
| 1.2 | 3.694 5 | 1.101 6×10-4 | ||
| 3 | 不考虑环境因素 | 1.3 | 3.601 1 | 1.584 4×10-4 |
| 1.4 | 3.520 1 | 2.156 9×10-4 | ||
| 1.5 | 3.444 9 | 2.856 4×10-4 | ||
| 1.6 | 3.301 6 | 4.806 8×10-4 | ||
| 0.0 | 3.339 4 | 4.198 0×10-4 | ||
| 1.2 | 3.143 7 | 8.341 3×10-4 | ||
| 4 | 不考虑作业因素 | 1.3 | 3.077 7 | 1.043 0×10-3 |
| 1.4 | 2.989 9 | 1.395 3×10-3 | ||
| 1.5 | 2.911 4 | 1.799 1×10-3 | ||
| 1.6 | 2.818 7 | 2.410 9×10-3 |
在4种情况下,锥形应力节可靠度指标都随着井口倾斜角的增大而不断减小,失效概率不断增大。这是因为在井口倾斜的过程中,立管系统整体应力变大,施加在锥形应力节模型顶端的载荷变大,进而导致失效概率变大。通过对比第一种情况与第二种情况可以看出,在不同井口倾斜角下,同时考虑环境和作业因素得到的可靠度计算结果明显偏低,在井口不倾斜的情况下可靠度指标降低了约25.5%,在井口倾斜1.6°的情况下可靠度指标降低了约25.7%。在第三种和第四种情况下,锥形应力节可靠度指标与第一种情况相比均有一定程度的降低,但在同一倾斜角下,环境因素会造成可靠度评估结果降低19%左右,作业因素只有6%左右。考虑不同随机变量情况下,锥形应力节可靠度指标随井口倾斜角的变化规律如图 7所示。
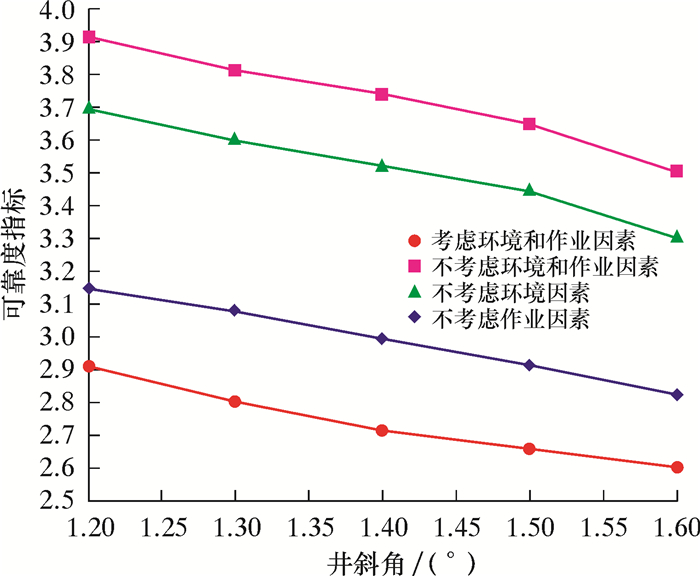
|
| 图 7 锥形应力节可靠度指标随井口倾斜角的变化曲线 Fig.7 The effect of wellhead inclination angle on the reliability index of the tapered stress joint |
结合表 4和图 7可知,在不考虑环境和作业因素对锥形应力节进行可靠性分析会导致可靠度计算结果偏高,造成结构评估的不准确,这会对结构的安全性造成影响。因此,在锥形应力节可靠度设计时应重点考虑环境因素和作业因素对结构的影响,其中环境因素对锥形应力节的可靠度指标影响相对较大。同时由图 7可以看出,在井口倾斜1.5°时,锥形应力节可靠性指标为2.656 9,根据船舶行业钢结构的可靠度安全值(3~4)可知,锥形应力节在极限井口倾斜角下作业偏于危险,应当控制井口倾斜角度,以提高锥形应力节的可靠性。
4 结论(1) 建立了井口倾斜1.5°时锥形应力节有限元分析模型,研究了不同井口倾斜角下锥形应力节的应力响应。计算结果表明,随着井口倾斜角的不断增大,结构应力最大值不断增大,但均未超出结构材料的屈服强度;结构的应力分布规律基本一致,最大值均出现在附带立管与锥形应力节连接位置,且在此处发生了明显的应力集中现象。
(2) 考虑作业因素、环境因素和结构因素的随机性,采用Kriging模型法建立了可靠性分析模型,开展了不同井口倾斜角下的可靠度指标计算。结果表明,随着井口倾斜角的增大,结构的失效概率不断增大,因此在作业过程中应控制井口的倾斜角度。
(3) 研究了环境和作业因素对锥形应力节可靠度计算结果的影响,确定了锥形应力节可靠性设计准则。在不考虑环境和作业因素随机性的情况下进行锥形应力节可靠度评估会造成失效概率明显降低,环境因素对可靠性结果的影响相对更大。在锥形应力节可靠性设计时,应全面考虑环境因素和作业因素的影响,以保证可靠度计算结果的准确性。
| [1] |
李清平. 我国海洋深水油气开发面临的挑战[J]. 中国海上油气(工程), 2006, 18(2): 130-133. LI Q P. The situation and challenges for deepwater oil and gas exploration and exploitation in China[J]. China Offshore Oil and Gas, 2006, 18(2): 130-133. |
| [2] |
阎岩, 张崎, 黄一. 基于张力腿平台的顶张紧式立管碰撞分析[J]. 上海船舶运输科学研究所学报, 2012, 35(1): 1-6. YAN Y, ZHANG Q, HUANG Y. Analysis of collisions between top tension risers on a tension leg platform[J]. Journal of Shanghai Ship and Shipping Research Institute, 2012, 35(1): 1-6. |
| [3] |
畅元江, 张伟国, 韩彬彬, 等. 张力腿平台丛式立管安装作业窗口分析[J]. 中国海上油气, 2017, 29(5): 126-133. CHANG Y J, ZHANG W G, HAN B B, et al. Envelopes for the installation operation of TLP cluster risers[J]. China Offshore Oil and Gas, 2017, 29(5): 126-133. |
| [4] |
LIM F K, MANNING B V G, ALFSTAD O. Snorre field TLP rigid riser system: an overview[R]. SPE 23086-MS, 1991.
|
| [5] |
MYERS R J, DELGADO J H. Jolliet TLWP well system[R]. OTC, 6401-MS, 1990.
|
| [6] |
FREUDENTHAL A M. Safety of structures[M]. [S.l.]: ASCE, 1947: 125-180.
|
| [7] |
KARUNAKARAN D, OLUFSEN A. Reliability analysis of a deep-water flexible riser system[C]//Proceedings of the 5th 1995 International Offshore and Polar Engineering Conference. Hague, Netherlands: International Society of Offshore and Polar Engineering, 1995: 365-372.
|
| [8] |
LERIA B J, TORHAUG R, KIRKVIK R H, et al. Reliability aspects of deep-water riser design[C]//Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering. OMAE, 1997: 315-325.
|
| [9] |
戴伟.基于响应面方法的立管结构可靠性研究[D].哈尔滨: 哈尔滨工程大学, 2012. DAI W. Research on riser structrual reliability based on response surface method[D]. Harbin: Harbin Engineering University, 2012. |
| [10] |
BAUGUS V, BAXTER C, TRIM A. Use of titanium taper joints in risers: the Neptune field and future designs[C]//17th International Conference on Offshore Mechanics and Arctic Engineering. USA: American Society of Mechanical Engineers, 1998.
|
| [11] |
CUNLIFFE N, MCCARTHY T J, TRIM A. Optimisation of tapered stress joints for offshore catenary risers[J]. Structural Engineer, 2003, 81(20): 35-40. |
| [12] |
MENICONI L C M, REID S R, SODEN P D. Preliminary design of composite riser stress joints[J]. Composites Part A:Applied Science and Manufacturing, 2001, 32(5): 597-605. DOI:10.1016/S1359-835X(00)00165-2 |
| [13] |
郑文青, 杨和振. 深海钢悬链立管应力接头的多轴疲劳分析[J]. 哈尔滨工程大学学报, 2011, 32(11): 1422-1427. ZHENG W Q, YANG H Z. Multiaxial fatigue analysis of the stress joint for a deepwater steel catenary riser[J]. Journal of Harbin Engineering University, 2011, 32(11): 1422-1427. |
| [14] |
张日曦.深水钢质立管弯曲抑制装置的关键技术研究[D].大连: 大连理工大学, 2013. ZHANG R X. The anti-bending technology of deep-water steel risers[D]. Dalian: Dalian University of Technology, 2013. |
| [15] |
JIANG S H, LI D Q, PHOON K K. A comparative study of response surface method and stochastic response surface method for structural reliability analysis[J]. Engineering Journal of Wuhan University, 2012, 45(1): 46-53. |
| [16] |
LOPHAVEN S, NIELSEN H, SONDERGAARD J. DACE-A MATLAB kriging toolbox[M]. [S.l.]: Caroline, 1998.
|
| [17] |
SAKATA S, ASHIDA F, ZAKO M. An efficient algorithm for Kriging approximation and optimization with large scale sampling data[J]. Computer Methods in Applied Mechanics and Engineering, 2004, 193(3/4/5): 385-404. |
| [18] |
GIUNTA A A, BALABANOV V, HAIM D, et al. Multidisciplinary optimization of a supersonic transport using design of experiments theory and response surface modeling[J]. Aeronautical Journal, 1997, 101(1008): 347-356. |
| [19] |
畅元江, 宋强, 张浩, 等. 台风条件下TLP串行立管系统碰撞分析[J]. 船舶力学, 2017, 21(5): 633-641. CHANG Y J, SONG Q, ZHANG H, et al. Collision analysis of risers in tandem for TLP under typhoon[J]. Journal of Ship Mechanics, 2017, 21(5): 633-641. |
| [20] |
TEIXEIRA A P, SOARES C G, NETTO T A, et al. Reliability of pipelines with corrosion defects[J]. International Journal of Pressure Vessels and Piping, 2008, 85(4): 228-237. DOI:10.1016/j.ijpvp.2007.09.002 |
| [21] |
畅元江, 王康, 张伟国, 等. 台风下TLP立管系统可靠性评估[J]. 海洋工程, 2017, 35(4): 1-7. CHANG Y J, WANG K, ZHANG W G, et al. Reliability assessment of TLP riser system under typhoon[J]. The Ocean Engineering, 2017, 35(4): 1-7. |
| [22] |
WANG G G, SHAN S. Review of metamodeling techniques in supports of engineering design optimization[J]. Journal of Mechanical Design, 2007, 129(4): 370-380. DOI:10.1115/1.2429697 |



