2. 中国石化集团国际石油勘探开发有限公司;
3. 中国石油大学(北京)油气资源与探测国家重点实验室
2. Sinopec International Petroleum Exploration and Production Corporation;
3. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum(Beijing
0 引言
高温射流是一种适用于深部硬地层油气开采的新型钻井技术[1],其结合了水射流钻井和高温热裂解破岩两者的优势。在实际钻井过程中,将燃料和氧气经过连续管注入井底反应腔,在深部井底高温高压(温度>650 K,压力>22 MPa)条件下,反应腔内发生超临界氧化反应,在反应过程中,燃料、氧化剂和水混为一相,能够消除潜在的界面质量传输阻力,使氧化过程快速进行[2-3]。反应主要产物水和二氧化碳处于超临界状态,利用高温和射流冲击力双重效应对井底岩石进行破碎[1]。
J.SIERRA-PALLARES等[4]对水射流中超临界与亚临界的过渡区进行了数值模拟研究,研究结果表明,当压力远高于临界点时,超临界区域内流体的流动特征更接近亚临界状态。M.J.SCHULER等[5-6]确定了临界压力附近模拟射流流场较为合适的普朗特数。在高温射流方面,文献[7]已对高温射流常压下的高温射流生成燃烧模型进行了优化。文献[8-9]对不同条件下(单孔、多孔喷嘴等)的流场进行了初步研究。但大多数针对高温射流流场的模拟研究都仅考虑了超临界水相,忽略了同时存在的少量二氧化碳和井底固相岩屑。文献[10]对高温射流三相井底流场进行了稳态分析。本文进一步对不同相态、多物质条件下的井底流场进行瞬态分析,并考虑不同地层岩屑直径大小对井底流场的影响,模拟条件更加符合实际钻井井底状况。
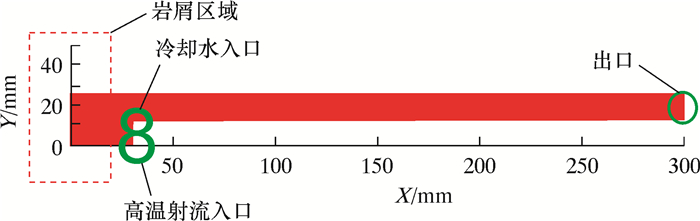
1 模型建立 1.1 几何模型为了缩短模拟时间、降低计算成本,采用二维中心截面代表真实的三维情况,流场几何模型如图 1所示。高温射流(超临界水和超临界二氧化碳混合物)从井下中心喷嘴射出,并设置为速度入口边界,其值为100 m/s,温度为700 K。根据甲烷与氧气化学反应系数,超临界水体积分数为70%,超临界二氧化碳体积分数为30%。冷却水从中心喷嘴两侧喷出对环空进行冷却,设置为速度入口边界,其值为20 m/s,温度为300 K。环空出口设置为流出边界。所模拟井段为井深3 000 m区域,设置操作压力为30 MPa,井底可以根据模拟条件是否设置岩屑区域,并采用Gambit软件生成结构化网格。
模型长度300 mm,井筒直径50.8 mm,连续管直径25.4 mm,射流喷嘴直径10 mm,冷却水入口直径10 mm。
1.2 热物理性质参数与求解在本文模拟条件下,存在两相超临界流体(超临界水和超临界二氧化碳)及高压低温液态的冷却水。因此,模拟流场为多相不同相态的流动传热过程。
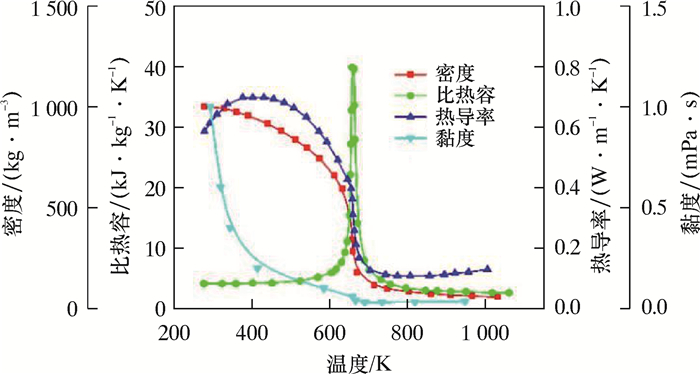
假设井底为恒压力条件(30 MPa),对于水在不同温度下的热物理性质变化,采用NIST提供的标准数据,如图 2所示[10]。对于二氧化碳在不同温度下的热物理性质,采用被广泛应用的Peng-Robinson模型来模拟。该模型可以相对准确地预测非极性流体和微极性流体的蒸汽压、密度和其他热力学性质[11-14]。由于水在超临界条件下更接近非极性,而其他物质(氧气和二氧化碳)也是非极性,所以采用Peng-Robinson状态方程进行模拟。
|
| 图 2 30 MPa下水的热物理性质变化 Fig.2 Thermophysical properties of water at 30 MPa |

|
(1) |
式中:p为绝对压力,Pa;V为比摩尔体积,L/mol;T为温度,K;R为通用气体常数,J/(mol·K);系数α1、b、c、δ和τ是临界温度Tc、临界压力pc、离心因子ζ和临界体积Vc的函数。
引力系数α1为:
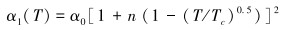
|
(2) |
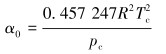
|
(3) |
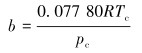
|
(4) |
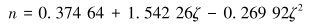
|
(5) |
此外,δ=2b,τ=-b2,c=0。
为了求解模拟的多相态井下流场,基于FLUENT软件[15],采用Realizable k-ε湍流模型、Eulerian多相流模型、连续性方程和能量方程等模型,利用Coupled算法求解,松弛因子为默认值,收敛精度设置为10-4,并进行了网格的无关性检验。
2 结果分析 2.1 稳定井下流场分析在持续钻井过程中,井下流场处于稳定状态。稳态条件下井下水(超临界水和冷却水)体积分数、温度和速度分布云图如图 3所示。井下水包含超临界水和冷却水,两者在接触面进行剧烈的能量和动量交换。从图 3可以看出:在整个研究区域内,水所占比例较大,冷却水完全覆盖入口附近,并贴紧钻井管柱上返,从而有效地对管柱进行降温保护,防止高温失效破裂;中心高温射流作用在井底之后沿着井壁上返,体积分数基本保持不变,但在中心射流两侧的涡流区域体积分数较高;超临界水与冷却水之间的温度变化与过渡可以被模拟出来,两者之间存在一个很薄的过渡层,大约保持在550 K;在速度场中,中心射流的速度最大,为100 m/s,到达井底附近速度逐渐减小,在中心井底两侧的漫流速度较高,至井壁处上返。

|
| 图 3 稳态条件下井下水(超临界水和冷却水)体积分数、温度和速度分布云图 Fig.3 Volume fraction, temperature and velocity distribution of downhole water (supercritical water, cooling water) under steady-state conditions |
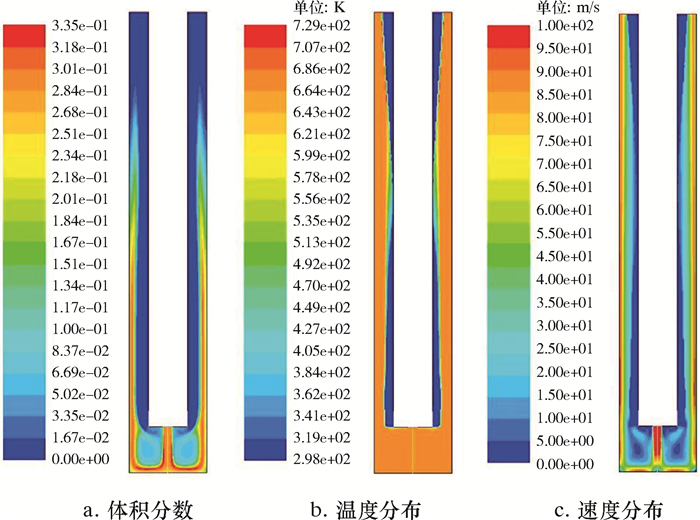
图 4为稳态条件下井下二氧化碳的体积分数、温度和速度分布云图。此处的二氧化碳同样经过了从超临界态到亚临界态的变化。二氧化碳的体积分数在整个流线中基本保持不变。此外,由于水相的体积分数包含了高温射流中的水和注入的冷却水,所以二氧化碳的分布可以较好地表示出射流流体的流动变化。从图 4可以看出:二氧化碳相的温度基本保持不变,这是由于在数值模拟过程中,所采用模型并未能较好地考虑二氧化碳相与冷却水相的热量交换,仅仅对同相(超临界水与冷却水)之间进行了较好地模拟,同时考虑单相和不同相之间的热量交换仍需进一步研究;二氧化碳的速度分布与水相基本相同。
|
| 图 4 稳态条件下井下二氧化碳体积分数、温度和速度分布云图 Fig.4 Volume fraction, temperature and velocity distribution of downhole carbon dioxide under steady state conditions |
2.2 瞬态井下流场分析
通过对瞬时条件下的流场进行分析,可以较好地展示流体热物理性质在不同时间的分布和变化。
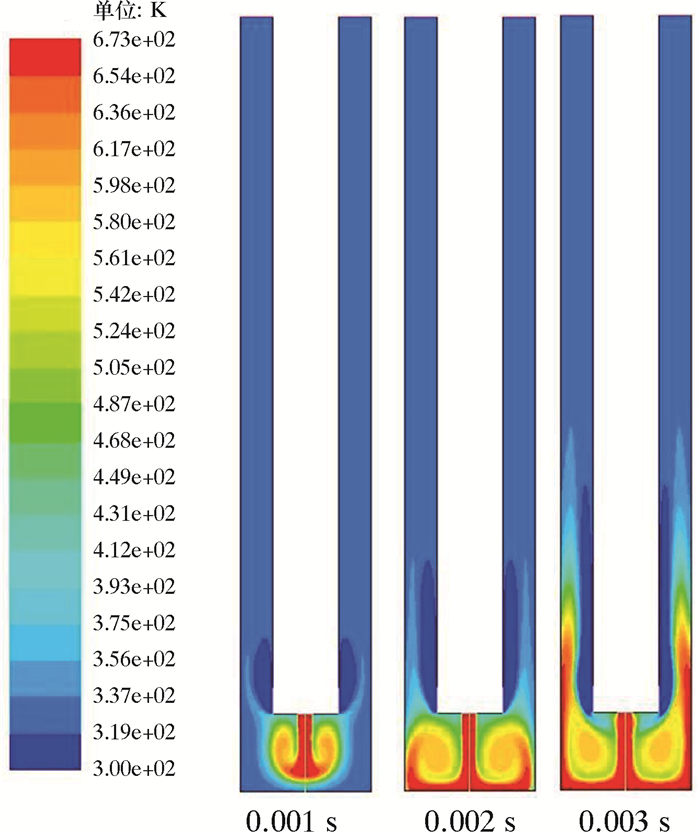
图 5表示射流初始过程0.001、0.002和0.003 s时的水相温度分布云图。井下初始条件为井筒内充满温度333 K的地层流体。从图 5可以看出:在0.001 s时,高温射流和冷却水刚刚进入井下,高温流体仍未到达井底,井内初始地层流体造成高温射流进行分散回流,同时两侧冷却水受上返高温流体和地层流体的影响而具有向上流动的趋势;在0.002 s时,高温射流到达井底,高温流体覆盖整个井底并开始上返,冷却水区域增加并沿钻井管柱上返;0.003 s时,井底高温、低温和过渡流场区域基本形成,流体继续上返。
|
| 图 5 瞬时条件下水相温度分布云图 Fig.5 Temperature distribution of water under transient conditions |
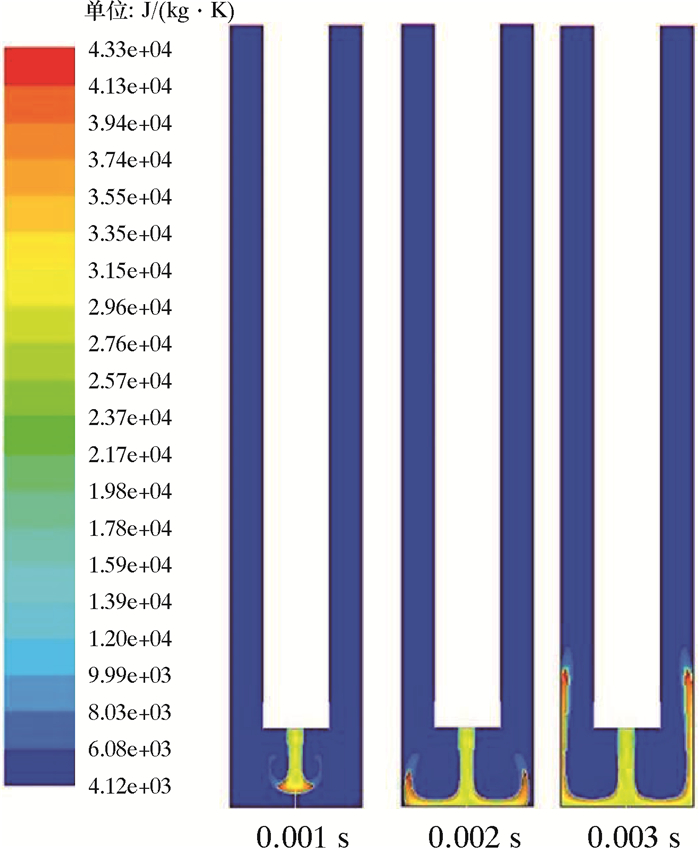
由于水的比热容在超临界态和亚临界态存在一个临界点,所以可以将水的比热容作为超临界水与亚临界水的边界。图 6为瞬时条件下水相比热容分布云图。
|
| 图 6 瞬时条件下水相比热容分布云图 Fig.6 Specific heat distribution of water under transient conditions |
从图 6可以看出:在0.001 s时,最大比热容出现在高温流体前缘,并形成完整的边界,同时处于超临界状态下的流体具有较高的比热容;在0.002和0.003 s时,最大比热容均处在超临界流体边界,可以很好地捕捉超临界水和亚临界水的分布。
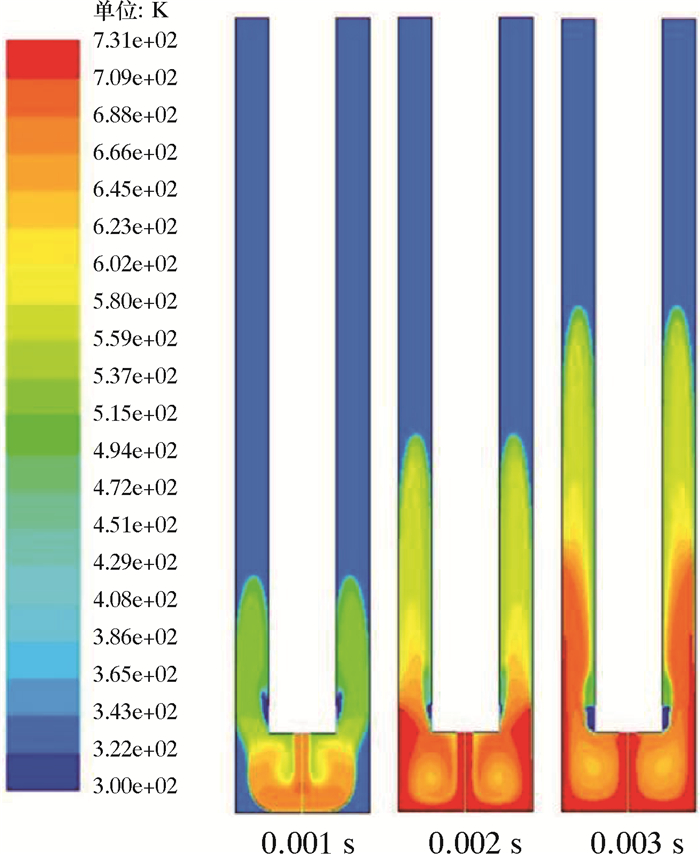
图 7为射流初始过程0.001、0.002和0.003 s时二氧化碳相温度分布。图 8为0.001 s时二氧化碳热物理性质分布云图。从图 8可以看出,大部分二氧化碳集中在高温射流出口附近,但是由于量程范围较大,其他区域的二氧化碳并不能很好地被表示出来,所以通过瞬时条件下的二氧化碳相温度分布(见图 7),可以更加准确地捕捉所有二氧化碳的分布。
|
| 图 7 瞬时条件下二氧化碳相温度分布云图 Fig.7 Temperature distribution of carbon dioxide under transient conditions |

|
| 图 8 0.001 s时二氧化碳热物理性质分布云图 Fig.8 Thermophysical properties distribution of carbon dioxide at 0.001 s |
将图 7中二氧化碳的温度分布与图 8中密度和比热容对应,可以看到在不同温度位置,对应的二氧化碳密度和比热容较为准确,这说明所采用的Peng-Robinson状态方程可以较为准确地对二氧化碳性质进行模拟。
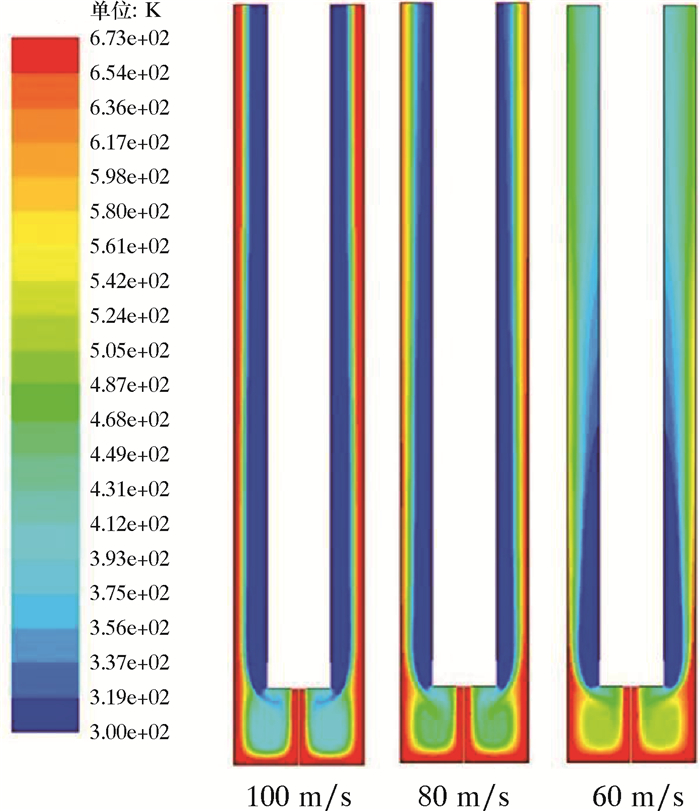
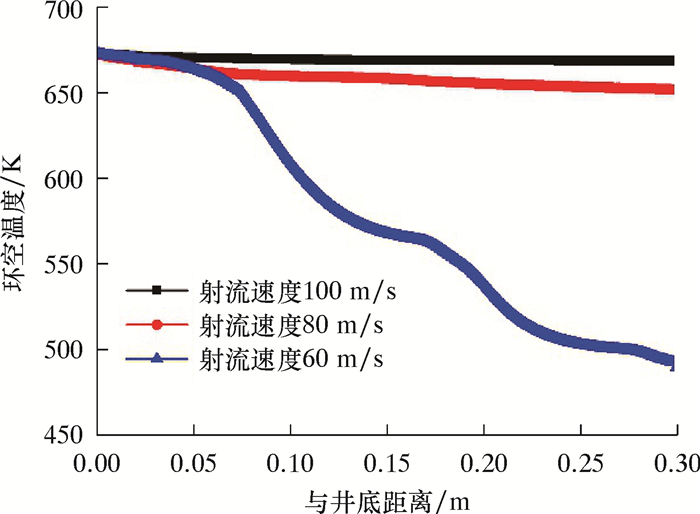
2.3 不同高温射流速度环空冷却分析如图 9所示,当保持冷却水注入速度恒定时,逐渐减小高温射流速度,环空温度将逐渐降低,高温与低温流体边界逐渐模糊,钻井管柱下部区域温度升高。选取环空中心线代表环空总体温度,如图 10所示,在不同射流速度下,井底部分(冷却水入口以下)温度基本保持不变。当射流速度从100 m/s降到80 m/s时,环空温度从673 K降到约650 K,降温幅度较小。当射流速度从80 m/s降低到60 m/s时,环空温度从650 K降到约500 K,降温幅度较大。在实际钻井过程中,可以通过控制高温射流与冷却水的注入比例来调节环空温度,从而防止出现高温井壁坍塌等事故。
|
| 图 9 不同射流速度时温度分布云图 Fig.9 Temperature distribution under different jet velocities |
|
| 图 10 不同射流速度时环空温度对比 Fig.10 Comparison of annulus temperatures under different jet velocities |
2.4 不同岩屑直径瞬态模拟分析
钻井过程中,高温射流在不同地层所产生的岩屑形状、大小可能不同。假设岩屑均为球形颗粒,仅考虑岩屑直径大小对射流流场的影响,并将岩屑放在井底区域模拟高温射流清岩过程。
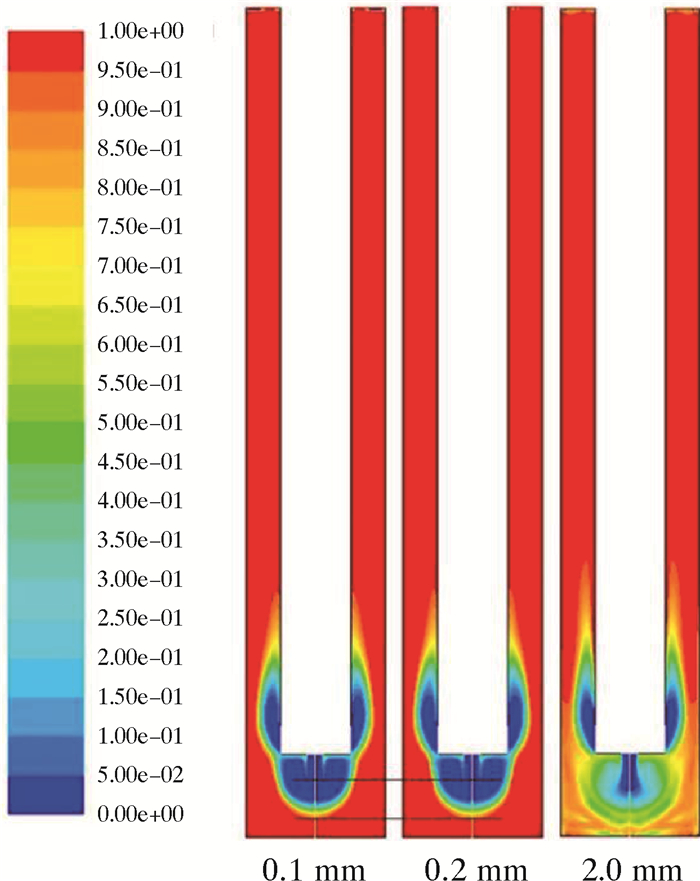
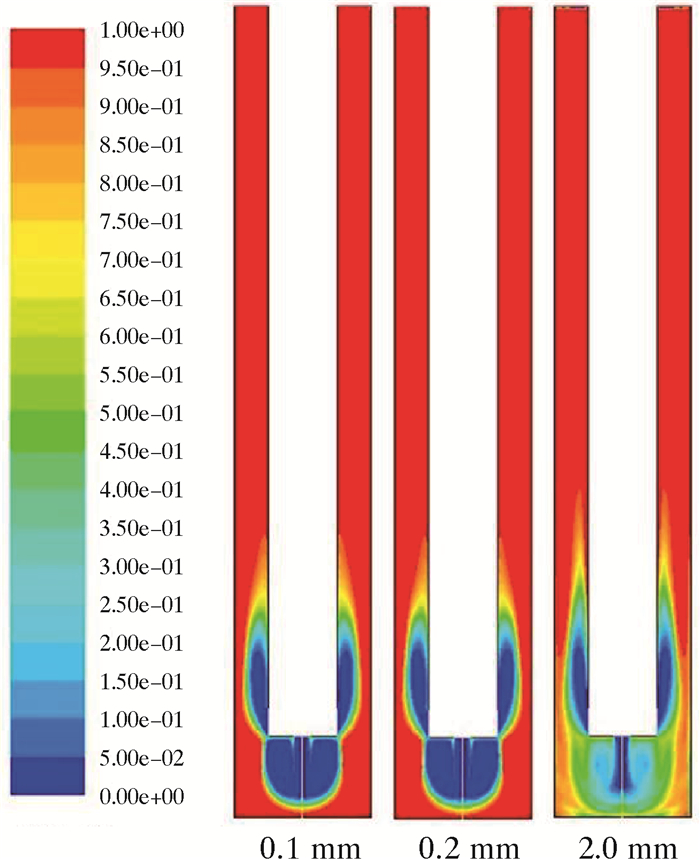
图 11和图 12分别为模拟0.001 0和0.001 5 s时不同岩屑直径的冲击流场。从图 11和图 12可以看出:在相同时间内,不同岩屑直径的冲击流场不同;岩屑直径越大,高温射流作用的区域越大;当岩屑直径从0.1 mm增加至0.2 mm时,冲击流场变化较小,冲击前缘稍向前;但是当岩屑直径从0.2 mm增加至2.0 mm时,冲击流场变化明显,清岩效果较好。这是因为井底空间有限,当岩屑直径增大后,岩屑总量减少,堆积疏松,这样在相同射流作用下更加易于清理。
|
| 图 11 0.001 0 s时不同直径岩屑体积分数 Fig.11 Volume fraction of cuttings with different diameters at 0.001 0 s |
|
| 图 12 0.001 5 s时不同直径岩屑体积分数 Fig.12 Volume fraction of cuttings with different diameters at 0.001 5 s |
3 结论
笔者对不同相态、多物质条件下高温射流钻井井底流场进行了瞬态分析,并考虑不同地层的岩屑直径大小对井底流场的影响,得到如下结论。
(1) 注入的冷却水贴紧钻井管柱上返,可以有效地对管柱进行降温保护,防止管柱高温失效破裂;超临界水与冷却水之间的温度变化与过渡可以被模拟出来,两者之间存在一个很薄的过渡层,最大比热容值均处在超临界流体边界,可以很好地捕捉超临界水和亚临界水的分布。
(2) 采用Peng-Robinson状态方程可以较为准确地对二氧化碳的热物理性质进行模拟,在实际钻井过程中,可以通过控制高温射流与冷却水的注入比例来调节环空温度,从而防止出现高温井壁坍塌等事故。
(3) 岩屑直径越大,高温射流作用的区域越大,更加易于清理。
(4) 研究结果可以为高温射流钻井提供理论依据。
| [1] |
崔柳, 汪海阁, 纪国栋, 等. 高温射流井底流场与参数影响分析[J]. 石油机械, 2017, 45(5): 1-9. CUI L, WANG H G, JI G D, et al. Analysis of downhole flow field and parameter effect in hydrothermal jet drilling[J]. China Petroleum Machinery, 2017, 45(5): 1-9. |
| [2] |
YAN Q H, HOU Y W, LUO J R, et al. The exergy release mechanism and exergy analysis for coal oxidation in supercritical water atmosphere and a power generation system based on the new technology[J]. Energy Conversion and Management, 2016, 129: 122-130. DOI:10.1016/j.enconman.2016.09.091 |
| [3] |
XU D H, HUANG C B, WANG S Z, et al. Characteristics analysis of water film in transpiring wall reactor[J]. International Journal of Heat and Mass Transfer, 2016, 100: 559-565. DOI:10.1016/j.ijheatmasstransfer.2016.04.090 |
| [4] |
SIERRA-PALLARES J, SANTIAGO-CASADO P, CASTRO F. Numerical modelling of supercritical submerged water jets in a subcritical co-flow[J]. The Journal of Supercritical Fluids, 2012, 65: 45-53. DOI:10.1016/j.supflu.2012.02.028 |
| [5] |
SCHULER M J, ROTHENFLUH T, ROHR P R V. Simulation of the thermal field of submerged supercritical water jets at near-critical pressures[J]. The Journal of Supercritical Fluids, 2013, 75: 128-137. DOI:10.1016/j.supflu.2012.12.023 |
| [6] |
SCHULER M J, ROTHENFLUH T, ROHR P R V. Numerical analysis of penetration lengths in submerged supercritical water jets[J]. The Journal of Supercritical Fluids, 2013, 82: 213-220. DOI:10.1016/j.supflu.2013.07.017 |
| [7] |
LYU Z H, LI G S, SONG X Z, et al. Comparative numerical analysis and optimization in downhole combustion chamber of thermal spallation drilling[J]. Applied Thermal Engineering, 2017, 119: 481-489. DOI:10.1016/j.applthermaleng.2017.03.070 |
| [8] |
SONG X Z, LYU Z H, LI G S, et al. Numerical analysis of the impact flow field of multi-orifice nozzle hydrothermal jet combined with cooling water[J]. International Journal of Heat and Mass Transfer, 2017, 114: 578-589. DOI:10.1016/j.ijheatmasstransfer.2017.06.106 |
| [9] |
SONG X Z, LYU Z H, LI G S, et al. Numerical analysis of characteristics of multi-orifice nozzle hydrothermal jet impact flow field and heat transfer[J]. Journal of Natural Gas Science and Engineering, 2016, 35: 79-88. DOI:10.1016/j.jngse.2016.08.013 |
| [10] |
SONG X Z, LYU Z H, WANG H Z, et al. Numerical analysis of the three-material downhole flow field in hydrothermal jet drilling[C]//WJTA-IMCA Conference and Expo, October 25-27, 2017.
|
| [11] |
NEGRO S, BIANCHI G M. Superheated fuel injection modeling:an engineering approach[J]. International Journal of Thermal Sciences, 2011, 50(8): 1460-1471. DOI:10.1016/j.ijthermalsci.2011.03.028 |
| [12] |
LANDUCCI G, D'AULISA A, TUGNOLI A, et al. Modeling heat transfer and pressure build-up in LPG vessels exposed to fires[J]. International Journal of Thermal Sciences, 2016, 104: 228-244. DOI:10.1016/j.ijthermalsci.2016.01.002 |
| [13] |
PENG D Y, ROBINSON D B. A new two-constant equation of state[J]. Industrial and Engineering Chemistry Fundamentals, 1976, 15(1): 59-64. DOI:10.1021/i160057a011 |
| [14] |
陈霖. CO2管道介质泄漏体积分数分布及危险区域实验[J]. 油气储运, 2017, 36(10): 1162-1167. CHEN L. Experiment on the medium volume fraction distribution and hazardous area in the case of CO2 pipeline leakage[J]. Oil & Gas Storage and Transportation, 2017, 36(10): 1162-1167. |
| [15] |
ANON.ANSYS FLUENT theory guide[Z].[S.l.]: ANSYS InC. 2011.
|