2. 冀东油田公司机械公司钻采设备分公司
2. Petroleum Machinery Company of PetroChina Jidong Oilfield Company
0 引言
目前,随钻测量(MWD)技术广泛应用于各种钻井过程中。钻井液压力波是传输井下信号最为经济可靠的方式,国际上普遍采用钻井液正脉冲信号发生器传输数据。但是,随着所需传输的参数越来越多,钻井液正脉冲传输方式已经不能满足钻井过程中数据传输的要求。采用钻井液压力多进制相移键控(MPSK)方式进行数据调制,是进一步提高井下数据信息传输速率的有效方法。国外基本采用连续压力波发生器结合钻井液压力正交相移键控(QPSK)调制技术以频带方式进行井下数据传输,信息传输速率可达16 bit/s[1]。
笔者通过对旋转阀式连续压力波信号发生器的控制逻辑进行分析,提出了一种双周期钻井液压力波信号QPSK调制方案。该方案对于后续深入研究连续波钻井液脉冲数据传输系统的信号解调方法,高速有效地实现井下数据上传具有重要意义。
1 国内外研究现状有关钻井液连续压力波无线随钻测量系统,Schlumberger和BakerHughes等公司已对该项技术掌握得相当成熟[2-3]。Schlumberger公司采用的信号编码方式有CPFSK(连续频移键控)和QPSK等方式。BakerHughes公司推出的信号发生器采用的编码方式不仅包括相位调制(PSK)或频率调制(FSK),还包括振幅调制(ASK)以及ASK与FSK调制相结合。目前根据Schlumberger公司PowerPluse旋转阀相关文献[4],钻井液连续压力波QPSK信号的码元周期由4个载波周期组成,并且在第1个载波周期内完成相位的调制,其他3个载波周期传送3个标准载波。沈跃等[5]研究的QPSK或者MPSK都采取4个载波周期,信息传输速率为载波频率的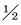
为了进一步加快传输速率,笔者设计了钻井液连续压力波双周期QPSK信号。该信号传输速率等于载波频率,传输速率提高一倍,带宽利用率提高一倍,为连续波无线随钻测量系统的研制提供了理论指导。
2 双周期QPSK信号的调制方案钻井液连续压力波双周期QPSK信号调制方案设计原理是:通过基带数据形成的可变幅度脉冲序列对载波相位进行调制产生QPSK信号。脉冲序列中每个脉冲的幅度对应QPSK信号在第1个载波周期内的相位。由于脉冲序列可分解为多个不同延时出现的单脉冲,则脉冲序列对载波相位的调制过程可以看作是多个单脉冲共同对载波进行调制的过程。
钻井液连续压力波双周期QPSK信号的调制方案包括基带信号控制规则、数学建模、调整波控制规则和解调规则4部分。
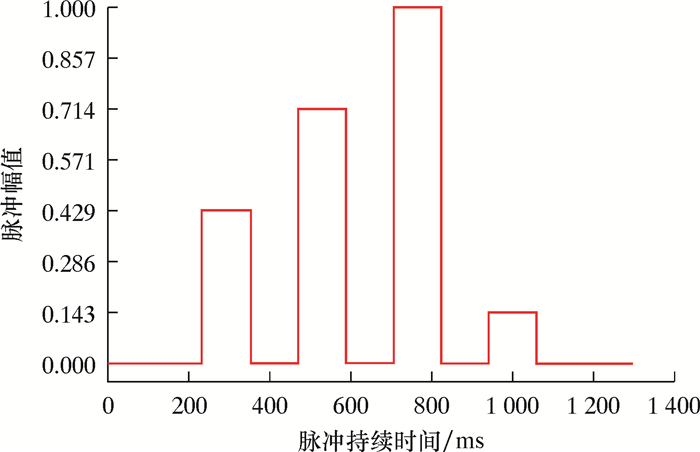
2.1 双周期QPSK基带信号控制规则变幅度矩形脉冲序列如图 1所示。四进制编码“00”、“01”、“10”和“11”对应的变幅矩形脉冲有4种,分别为1/7、3/7、5/7和1。
|
| 图 1 变幅度矩形脉冲序列 Fig.1 Amplitude variable rectangular pulse sequence |
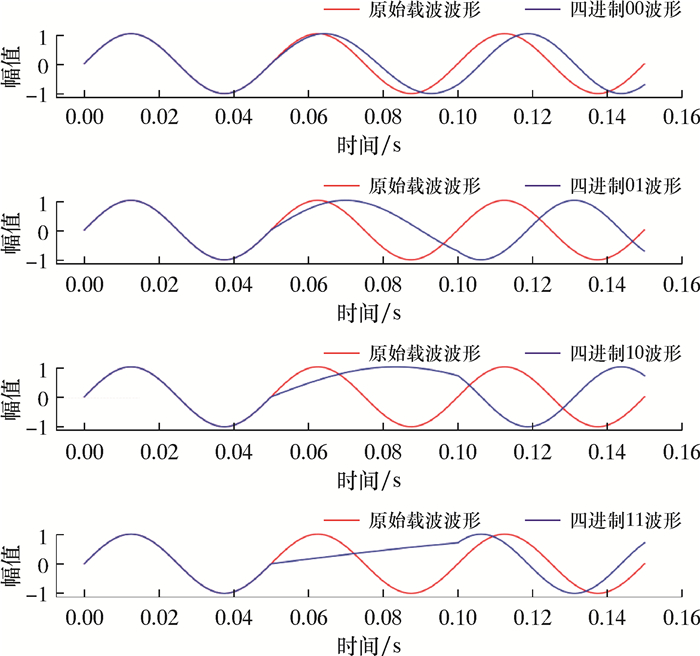
基带信号控制下产生的钻井液连续压力波双周期QPSK信号如图 2所示。其控制过程为:正常双周期载波,旋转阀角速度为ω;当四进制数字为“00”时,调制脉冲幅度为1/7,旋转阀以角速度7ω/8转动一个载波周期,然后以角速度ω转一个载波周期,相位差为π/4;当四进制数字为“01”时,调制脉冲幅度为3/7,旋转阀以角速度5ω/8转动一个载波周期,然后以角速度ω转一个载波周期,相位差为3π/4;当四进制数字为“10”时,调制脉冲幅度为5/7,旋转阀以角速度3ω/8转动一个载波周期,然后以角速度ω转动一个载波周期,相位差为5π/4;当四进制数字为“11”时,调制脉冲幅度为1,旋转阀以角速度ω/8转动一个周期,然后以角速度ω转动一个载波周期,相位差为7π/4。
|
| 图 2 四进制波形 Fig.2 Quaternary waveform |
2.2 双周期QPSK信号数学建模
根据上述工作原理,钻井液连续压力波双周期QPSK输出信号可以表示为[9-10]:
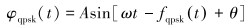
|
(1) |
式中:A为压力载波幅度,Pa;fqpsk(t)为相移函数;ω=2πfc为载波角角频率,rad/s,fc为载波频率,Hz;T=1/fc为载波周期,s;θ为载波初始相位,(°)。
脉冲序列由多个单脉冲组成。设MWD系统以10位二进制数作为一个数据传送单元,即C=C10C9C8C7C6C5C4C3C2C1,其中C为0或者1,每相邻两位二进制码元dm=bmCm组合成四进制码元,则MWD系统数据编码可以表示为C= b5c5b4c4b3c3b2c2b1c1 =d5d4d3d2d1。
根据上述调制过程,调制的逻辑脉冲序列函数L(t)表示为:
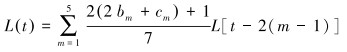
|
(2) |
根据调制规则,L(t)和钻井液连续压力波双周期QPSK信号为比例积分关系,得出t时刻相移量函数为:
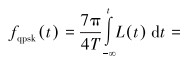
|
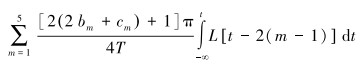
|
(3) |
将式(3)带入式(1),得出连续波QPSK信号数学模型为:
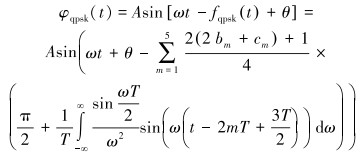
|
(4) |
钻井液连续压力波双周期QPSK调整波逻辑控制分为基带信号调整波的逻辑控制和结束调整波的逻辑控制。基带信号调整波针对每一位四进制基带信号的第二载波周期进行调整,满足基带信号控制规则。结束调整波针对一个数据传送单元传送完后的相位进行调整,满足最终相位差为2kπ,k为正整数。
根据钻井液连续压力波双周期QPSK信号控制规则[10],基带信号第二载波周期中,调整波的相位由前一位四进制码元产生的相位差以及本身相位差共同决定(见表 1)。θn-1为前一位四进制码元产生的相位差,单位为rad。
| 旋转阀角速度/(rad·s-1) | ω/8 | 3ω/8 | 5ω/8 | 7ω/8 | ω |
| 信号延时相位/rad | 7π/4 | 5π/4 | 3π/4 | π/4 | 2π |
| 调整波相位/rad | θn-1-7π/4 | θn-1-5π/4 | θn-1-3π/4 | θn-1-π/4 | θn-1-2π |
结束调整波由调整波1和调整波2组成。其调制相位由前5位四进制码元所产生的相位差的和以及最后一位四进制码元产生的相位共同决定。
中间10位随机产生的二进制数字调制后所得的相位总和由式(5)和式(6)决定:
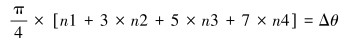
|
(5) |
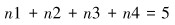
|
(6) |
式中:n1为“00”产生的相位差;n2为“01”产生的相位差;n3为“10”产生的相位差;n4为“11”产生的相位差;Δθ为“10”位随机二进制数相位差的和。
根据旋转阀控制逻辑分析,10位随机数字一共产生210=1 024种组合,根据对1 024种组合的统计分析,Δθ产生的相位差总的取值为离散固定值,为2kπ±π/4、2kπ±3π/4、2kπ±5π/4和2kπ±7π/4。
结束调整波逻辑,根据前10位二进制数字调制得出的最终相位差进行调整[11],调整结果如表 2所示。
| 总相位差/rad | 调整波1信号角速度/(rad·s-1) | 调整波2信号角速度/(rad·s-1) |
| 2kπ+π/4 | 7ω/8 | ω |
| 2kπ+3π/4 | 5ω/8 | ω |
| 2kπ+5π/4 | 3ω/8 | ω |
| 2kπ+7π/4 | ω/8 | ω |
| 2kπ-π/4 | ω/8 | ω |
| 2kπ-3π/4 | 3ω/8 | ω |
| 2kπ-5π/4 | 5ω/8 | ω |
| 2kπ-7π/4 | 7ω/8 | ω |
2.4 双周期QPSK信号的解调规则
根据三种聚类识别算法和模糊矩阵识别算法分别对实测波形进行预测分类,然后通过多数表决机对预测结果进行最终识别[12]。
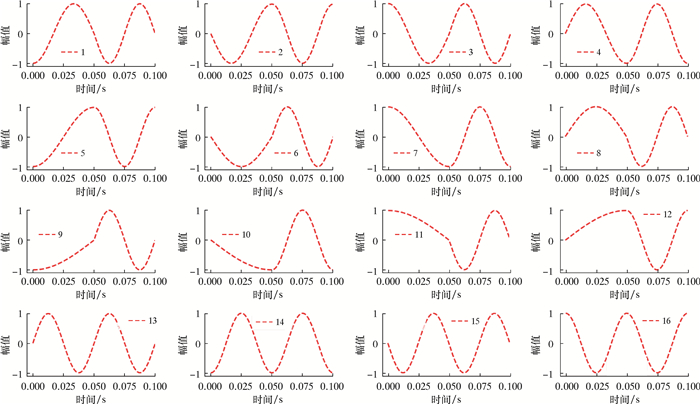
首先对钻井液连续压力波双周期QPSK信号进行十六类型分类,结果如图 3所示。
|
| 图 3 双周期QPSK信号分类 Fig.3 Two-cycle QPSK signal classification |
2.4.1 双周期QPSK信号的聚类识别算法
对实测的双周期QPSK信号和参考双周期QPSK信号进行离散化,提取数量为n的特征向量。参考模型特征向量Xref=(x1,x2,……,x16)T、经过噪声处理和基值调整后的实时采样钻井液脉冲特征向量Yreal=(y1,y2,……,y16)T。采用欧式距离、特征值夹角余弦和具有二值特征Tanimoto方法来计算两类数据的相似度。
欧式距离D为[13]:
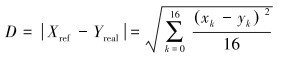
|
(7) |
首先对样本xk、yk进行归一化处理,采用极值归一法,将归一化数据压缩在(0,1)的区间内,则有:
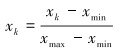
|
(8) |
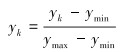
|
(9) |
式中:xk、yk为采样数据,xmin、ymin为采样数据中的最小值,xmax、ymax为采样数据中的最大值。
特征值夹角余弦S为[14]:
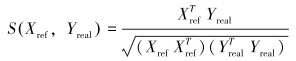
|
(10) |
具有二值特征Tanimoto测度为[15]:
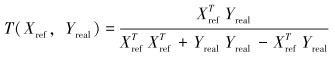
|
(11) |
采用聚类识别算法对实际信号进行处理时,窗口的滑动是以双周期内的滑动来进行依次识别,D越小,S和T值越大,表示两类数据之间的波形越相似。
2.4.2 双周期QPSK信号的模糊识别算法计算参考模型特征向量Xref和实时采样钻井液脉冲特征向量Yreal的斜方差矩阵,16种参考模型特征向量之间的协方差矩阵,然后将斜方差值按(Y,X1,X2,……,X16)顺序,写入模糊关系矩阵R[16],R=rij(i、j=1,2,3,……,16),其中rij= rji。
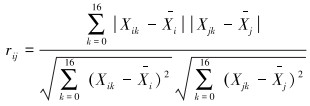
|
(12) |
式中:k为参考模型序号,Xik、Xjk为采样数据,Xi和Xj分别为第i行、第j行采样数据中的平均值。
识别样本模型和对应的四进制数据如表 3所示。根据计算的模糊关系矩阵值,设定阈值0.91,模糊系数大于给定阈值设置为1,小于阈值设置为0,得到阈值聚类的模糊矩阵对照表。将等价矩阵中每行为1的系数所对应的列归为同一类,输出聚类结果。然后根据多数表决机对结果进行表决。
| 样本模型 | 四进制数据(相位差) |
| 模型0 | 01(π/4) |
| 模型1 | 01(3π/4) |
| 模型2 | 01(5π/4) |
| 模型3 | 01(7π/4) |
| 模型4 | 10(π/4) |
| 模型5 | 10(3π/4) |
| 模型6 | 10(5π/4) |
| 模型7 | 10(7π/4) |
| 模型8 | 10(π/4) |
| 模型9 | 10(3π/4) |
| 模型10 | 10(5π/4) |
| 模型11 | 10(7π/4) |
| 模型12 | 11(π/4) |
| 模型13 | 11(3π/4) |
| 模型14 | 11(5π/4) |
| 模型15 | 11(7π/4) |
3 双周期QPSK仿真应用 3.1 双周期QPSK仿真过程
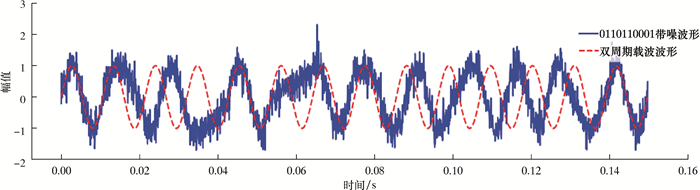
钻井液连续压力波双周期QPSK信号数据传送单元由启动波、数据波和结束调整波组成[17]。启动波形是频率为fc、相位与载波相差2kπ的一个周期的连续波;数据波是根据钻井液连续压力波双周期QPSK信号的基带信号控制规则、调整波控制逻辑所产生的10个周期的连续波;结束调整波是根据调整波控制逻辑所产生的2个载波周期的连续波,其中0110110001时域信号如图 4所示。
|
| 图 4 调制QPSK编码波形 Fig.4 Modulated QPSK coding waveform |
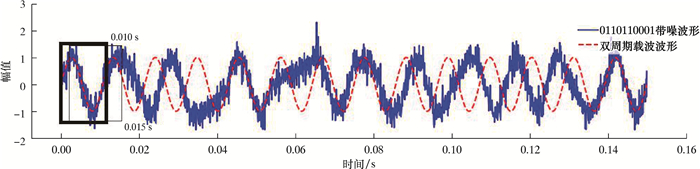
钻井液连续压力波双周期QPSK信号的解调采用聚类算法,其检测窗口如图 5所示。设载波频率fc=20 Hz,采样频率设定为4 000 Hz,一个载波周期的采样点数为200,选取扫描窗口宽度为202[18]。检测窗口以0 s时间开始一直到0.16 s,然后以0.005 bit/s的速度向右移动。
|
| 图 5 双周期QPSK编码检测窗口 Fig.5 Dual-cycle QPSK coding detection window |
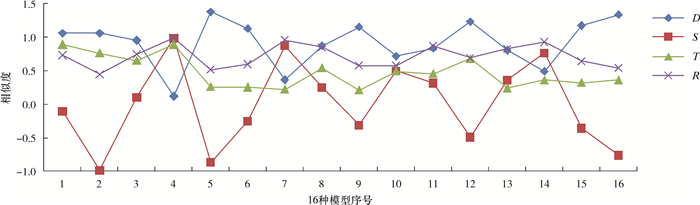
采样该时间段的数据点和标准波形模型进行匹配,聚类算法对信号进行解调,结果如图 6所示。第4种模型聚类识别中,D=0.119 935,S=0.985 909,T=0.89。
|
| 图 6 聚类算法分类结果 Fig.6 Clustering algorithm classification results |
根据式(12),模糊关系矩阵第5行为(0.985 532,-0.064 31,-0.488 74,-0.064 31),根据阈值分析其系数为(1,0,0,0),表明第4种模型和采样信号最为接近,判断为四进制数“10”(π/4)。
多数表机表明该段波形为四进制“10”。然后窗口继续移动到0.005~0.015 s进行下一个波形的判断。最终整个波形的判断0110110001,与仿真结果相符。
3.2 双周期QPSK仿真频谱分析钻井液连续压力波双周期QPSK信号以钻井液作为信道,传输过程中必将会受到噪声影响,由于是频带传输,所以频带内的噪声会严重影响信号在地面的准确检测。为了能把信号准确传输至地面,必须对钻井液连续压力波双周期QPSK信号进行频域特性分析,确定信号的频带宽度,从而在信号传输过程最大限度地避免同频噪声的影响[19]。
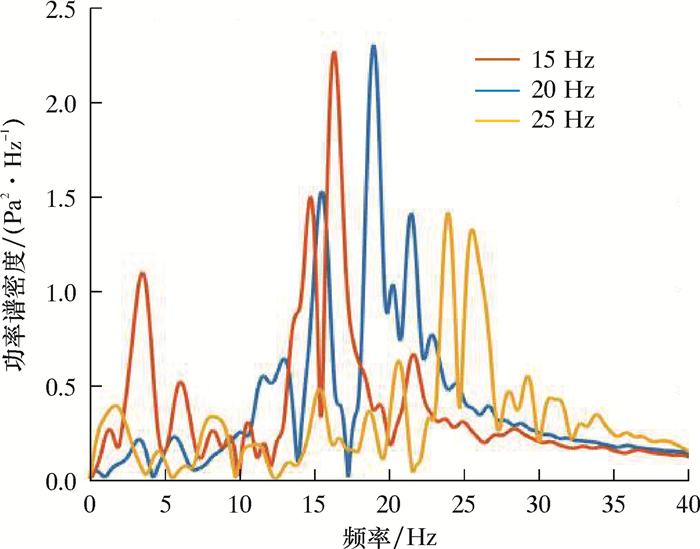
由式(3)可以看出,fqpsk(t)是由若干不同频率的正弦波组成,分析结果如图 7所示。由图 7可以看出,信号频谱主要集中在载频附近。通过Matlab数值计算可知,频带在15~25 Hz内信号功率占总功率的93%,频带内信号的频谱随载频移动。双周期QPSK要求两个载波周期传递2位二进制码元,即码元周期等于载波周期。因此,双周期QPSK信号码元传输速率Rb为0.5fc,信息传输速率为:
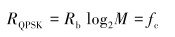
|
(13) |
|
| 图 7 双周期QPSK信号功率谱密度 Fig.7 Dual-cycle QPSK signal power spectral density |
Matlab数值计算结果如表 4所示。由表 4可知,信号的带宽虽然随着载波频率的改变而改变,但是带宽内能量基本不变,QPSK信号在带宽内的能量约为信号总能量的80.3%。双周期QPSK信号在频域内能量主要集中在载波频率附近,且信号存在明显的主瓣,副主瓣的能量远低于主瓣能量,能够满足频带传输要求[20]。信号的有效带宽也随着载波频率的变化而发生变化,载波频率越大,带宽越宽。当带宽减小时,频谱密度的幅度增加。
| 载波频率/Hz | 中心频率/Hz | 带宽/Hz | 带宽内能量比 | 传输速率/(bit·s-1) | 功率90%内有效带宽/Hz |
| 15 | 9.56 | 7.5 | 80.23 | 15 | 5.50~14.63 |
| 20 | 19.63 | 9.8 | 80.36 | 20 | 4.63~25.69 |
| 25 | 24.68 | 11.8 | 80.26 | 25 | 8.62~31.63 |
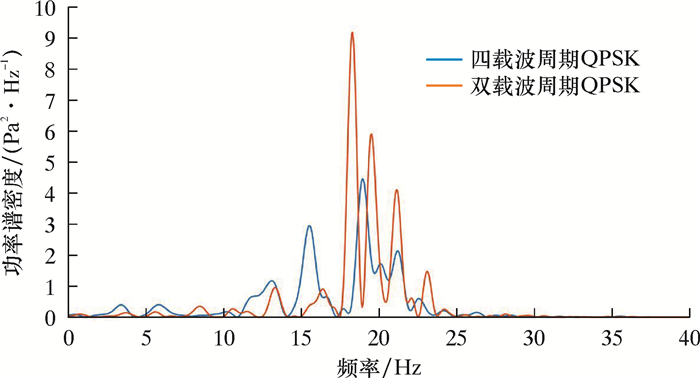
四载波周期QPSK与双载波周期QPSK功率谱密度比较图如图 8所示。
|
| 图 8 四载波周期QPSK与双载波周期QPSK功率谱密度比较 Fig.8 Comparison of power density of four carrier cycle QPSK and dual carrier cycle QPSK |
由图 8可知,双载波周期QPSK信号相对于四载波周期QPSK信号在带宽内的能量要集中,双载波周期QPSK信号幅度更高,检测效果更好,解调更容易。
Matlab数值计算如表 5所示。由表 5可知,相比四载波周期QPSK信号,双载波周期QPSK信号传输速度是四载波周期QPSK的2倍,频带利用率是四载波周期QPSK的2倍[21]。
| QPSK类型 | 载波频率/Hz | 传输速率/(bit·s-1) | 频带利用率/(bit·Hz-1·s-1) | 功率90%内有效带宽/Hz |
| 四载波周期 | 20 | 10 | 1/2 | 8.62~31.63 |
| 双载波周期 | 20 | 20 | 1 | 9.60~28.30 |
4 结论
(1) 通过变幅度数字基带信号控制旋转阀转速,可以实现钻井液压力双周期QPSK的调制。相对于钻井液连续压力波四周期QPSK调制,钻井液压力双周期QPSK调制在相同的带宽下,信息传输速率和频带利用率均提高一倍。
(2) 钻井液连续压力波双周期QPSK调制中,启动和结束波形的相位与载波同时刻的相位一致,有效地防止了前、后两个10位码元相位相互干扰。
(3) 设计钻井液连续压力波双周期QPSK的整体处理方案,建立了井口连续波信号的数学模型。基于该数学模型,仿真得出了不同频率下双周期QPSK信号调制的频谱特性。
(4) 对钻井液连续压力波四周期和双周期QPSK调制信号进行了频域分析,得出双周期QPSK钻井液压力调制的信息传输速率和频谱主瓣带宽内信号的相对能量较高,适用于井下数据的传输。
| [1] |
WANG H, SWEATMAN R, ENGELMAN B, et al. Best practice in understanding and managing lost circulation challenges[J]. SPE Drilling & Completion, 2008, 2(2): 168-175. |
| [2] |
沈跃, 张亨, 张令坦, 等. 基于自适应滤波的钻井液连续压力波信号噪声抑制[J]. 石油学报, 2014, 35(2): 353-358. SHEN Y, ZHANG H, ZHANG L T, et al. Eliminating noise of the drilling fluid continuous pressure wave signals based on the self-adaptive filtering method[J]. Acta Petrolei Sinica, 2014, 35(2): 353-358. |
| [3] |
李翠, 高德利, 沈跃. 钻井液压力脉宽及脉位多进制相移键控信号分析[J]. 石油学报, 2013, 34(1): 178-183. LI C, GAO D L, SHEN Y. Analysis of drilling fluid pressure MPSK signals for PWM and PPM[J]. Acta Petrolei Sinica, 2013, 34(1): 178-183. |
| [4] |
MARTIN C A, PHILO R M, DECKER D P, et al. Innovative advances in MWD[R].SPE 27516, 1994.
|
| [5] |
沈跃, 朱军, 苏义脑, 等. 钻井液压力正交相移键控信号沿定向井筒的传输特性[J]. 石油学报, 2011, 32(2): 152-156. SHEN Y, ZHU J, SU Y N, et al. Transmission characteristics of the drilling fluid pressure quadrature phase shiftkeying signal along a directional wellbore[J]. Acta Petrolei Sinica, 2011, 32(2): 152-156. |
| [6] |
刘新平.DSP控制连续波信号发生器机理与风洞模拟试验研究[D].东营: 中国石油大学(华东), 2009. LIU X P. Research on mechanism of continuous wave signal generator controlled by DSP and the wind tunnel simulation test[D]. Dongying: China University of Petroleum(Huadong), 2009. |
| [7] |
吴金勇.石油钻井中钻井液连续波信号处理方法研究[D].哈尔滨: 哈尔滨工业大学, 2012. WU J Y. Research on signal processing method of drilling fluid continuous wave in oil drilling[D]. Harbin: Harbin Institute of Technology, 2012. |
| [8] |
涂兵.MWD中泥浆脉冲信号辨识及地面适配技术研究[D].北京: 北京工业大学, 2013. TU B. MWD mud pulse signal identification and ground adaptation technology research[D]. Beijing: Beijing Industry University, 2013. |
| [9] |
刘修善, 苏义脑. 泥浆脉冲信号的传输速度研究[J]. 石油钻探技术, 2000, 28(5): 24-26. LIU X S, SU Y N. Study on transmission velocity of mud-pulsesignal[J]. Petroleum Drilling Techniques, 2000, 28(5): 24-26. |
| [10] |
WANG H, SOLIMAN M Y, TOWLER B F. Investigation of factors for strengthening a wellbore by propping fractures[J]. SPE Drilling & Completion, 2009, 24(3): 441-451. |
| [11] |
沈跃, 李翠, 朱军, 等. 钻井液压力多进制相移键控信号的数值建模及特性分析[J]. 中国石油大学学报(自然科学版), 2010, 34(5): 77-83. SHEN Y, LI C, ZHU J, et al. Numerical modeling and characteristics analysis of drilling fluid pressure MPSK signals[J]. Journal of China University of Petroleum(Edition of Natural Science), 2010, 34(5): 77-83. |
| [12] |
沈跃, 张令坦, 崔诗利, 等. 钻井液DPSK信号解调及旋转阀控制脉冲重构[J]. 石油机械, 2014, 42(8): 7-11. SHEN Y, ZHANG L T, CUI S L, et al. Phase demodulation of drilling fluid pressure DPSK signals and rotary valve control pulse reconstitution[J]. China Petroleum Machinery, 2014, 42(8): 7-11. |
| [13] |
BRANDON T L, MINTCHEV M P, TABLERH. Adaptive compensation of the mud pump noise in a measurement while drilling system[J]. SPE Drilling & Completion, 1999, 4(2): 128-133. |
| [14] |
沈跃, 张令坦, 曹璐, 等. 基于旋转阀控制脉冲重构的钻井液QPSK信号解码及误码率分析[J]. 中国石油大学学报(自然科学版), 2016, 40(6): 91-100. SHEN Y, ZHANG L T, CAO L, et al. Decoding of drilling pressure QPSK signals based on controlpulses reconstruction of rotary valve and bit error rate analysis[J]. Journal of China University of Petroleum(Edition of Natural Science), 2016, 40(6): 91-100. |
| [15] |
汤楠, 穆向阳. 调制式旋转导向钻井工具稳定平台控制机构研究[J]. 石油钻采工艺, 2003, 25(3): 9-12. TANG N, MU X Y. Study on the platform stabilizing control mechanism of modulating rotary steerable drilling tool[J]. Oil Drilling & Production Technology, 2003, 25(3): 9-12. |
| [16] |
王秉钧, 冯玉珉, 田宝玉. 通信原理[M]. 北京: 清华大学出版社, 2006: 58-61, 201-203.
|
| [17] |
边海龙, 苏义脑, 盛利民. 连续波随钻测量信号井下传输特性分析[J]. 仪器仪表学报, 2011, 32(5): 983-989. BIAN H L, SU Y N, SHENG L M. The measurement while drilling (MWD) continue-wave signal analysis based on downhole information transmission characteristic[J]. Chinese Journal of Scientific Instrument, 2011, 32(5): 983-989. |
| [18] |
KLOTZ C, BOND P, WASSERMAN I, et al. A new mud pulse telemetry system for enhanced MWD/LWD application[R].SPE 112683, 2008.
|
| [19] |
WASSERMAN I, HAHN D, NEUYEN D H A I, et al. Mud-pulse telemetry sees step-change improvement with oscillating shear valves[J]. Oil & Gas Journal, 2008, 106(24): 39-40. |
| [20] |
WINZER P J, DORRER C, ESSIAMBRE R J, et al. Chirped return-to-zero modulation by imbalanced pulse carver driving signals[J]. Photonics Technology Letters, 2004, 16: 1379-1381. DOI:10.1109/LPT.2004.826036 |
| [21] |
SWANSON E A, LIVAS J C, BONDURANT R S. High sensitivity optically preamplified direct detection DPSK receiver with active delay-line stabilization[J]. Photonics Technology Letters, 1994(6): 263-265. |


