2. 中海油能源发展股份有限公司工程技术分公司
2. CNOOC Ener Tech-Drilling & Production Co
0 引言
PDC钻头是目前钻井工程中应用最广的钻头,其在遇到严重的扭转振动时,会出现间歇性的黏滞和高速滑动的周期性振动,称为黏滑振动。一旦PDC钻头出现黏滑振动,易出现崩齿或损坏等情况,将大幅缩短使用寿命,增加钻井成本[1-7]。
关于PDC钻头的黏滑振动,国内外已经有较为深入的研究。T.RICHARD等[6]通过建立钻柱系统轴向和扭转耦合模型,指出钻柱黏滑振动与钻柱轴向振动直接相关。B.BESSELINK等[7]通过建立无轴向刚度和阻尼的动力学模型,分析了黏滑振动极限环的参数。LIN Y.Q.等[8]采用干摩擦模型,分析了转速和阻尼对黏滑振动的影响。C.GERMAY等[9]通过有限元法分析了黏滑振动的自激属性。祝效华等[10]分析了扰动及钻柱固有频率对PDC钻头黏滑振动的影响。韩春杰等[11]分析了摩阻对钻柱动态位移的影响。
虽然目前对PDC钻头的黏滑振动分析较多,但是大部分分析是基于所钻岩石为均质的情况。而随着PDC钻头技术的提高,其使用寿命有了大幅度的延长,使得单只钻头的进尺有所提高,这就使得PDC钻头钻遇不同地层的情况越来越多。从目前PDC钻头在现场应用的情况来看,其在钻硬地层及软硬交错地层时容易出现切削齿的崩齿而提前失效。因此,分析在岩石硬度发生改变的情况下PDC钻头的黏滑振动具有重要的应用价值,而且对钻井工程参数的优选及降本增效有很好的指导意义。
本文根据实际钻井工况,建立了PDC钻头处黏滑振动模型,对模型进行求解,并分析了PDC钻头在从软地层进入硬质地层时PDC钻头处的转速波动及相位图,同时分析了不同突变率情况下其黏滑振动情况。
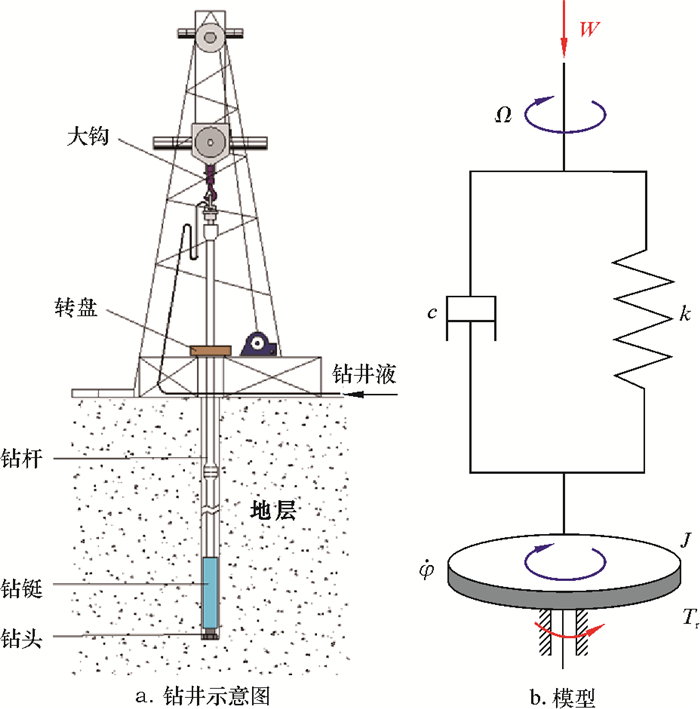
1 PDC钻头处黏滑振动模型分析在常规钻井过程中,PDC钻头接在钻铤的最下端,钻铤和钻杆通过螺纹连接并向上穿过转盘处,钻杆悬挂在大钩的下端,如图 1a所示。钻进时,电机驱动转盘转动,并带动钻杆、钻柱和PDC钻头转动来实现破碎岩石,大钩可以通过调节提拉力来调节钻头处钻压W的大小。
|
| 图 1 PDC钻头处扭转振动模型 Fig.1 Torsional vibration model of PDC bit |
整个钻杆系统主要包括钻杆和下部钻具组合(BHA)。分析钻头的黏滑振动时,将钻柱系统当作一个扭摆模型[12-16],其模型如图 1b所示。假设条件为:①直井;②钻柱和井壁之间不接触;③转盘转速恒定。将钻杆看成有一定扭转刚度的弹簧,钻井液对钻杆的转动有一定的阻尼作用,钻头和钻铤看成一个质量集中的转动盘。
此时,钻头处的扭矩平衡方程为[7]:

|
(1) |
式中:Ω为转盘转速,rad/s;Tr(t)为钻头处的阻力扭矩,N·m;c为阻尼系数;k为钻杆系统的扭转刚度,(N·m)/rad;J为钻杆系统的转动惯量,kg·m2,可由式(2)计算。
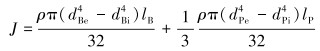
|
(2) |
式中:ρ为钻杆密度,kg/m3;dBe、dBi分别为BHA外径和内径,m;dPe、dPi分别为钻杆外径和内径,m;lB、lP分别为BHA长度和钻杆长度,m。
阻尼系数的表达式为:
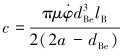
|
(3) |
式中:μ为钻头切削齿和岩石之间的摩擦因数;a为钻头直径,m。
钻杆系统的扭转刚度表达式为:
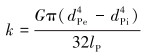
|
(4) |
式中:G为钻杆剪切模量,Pa。
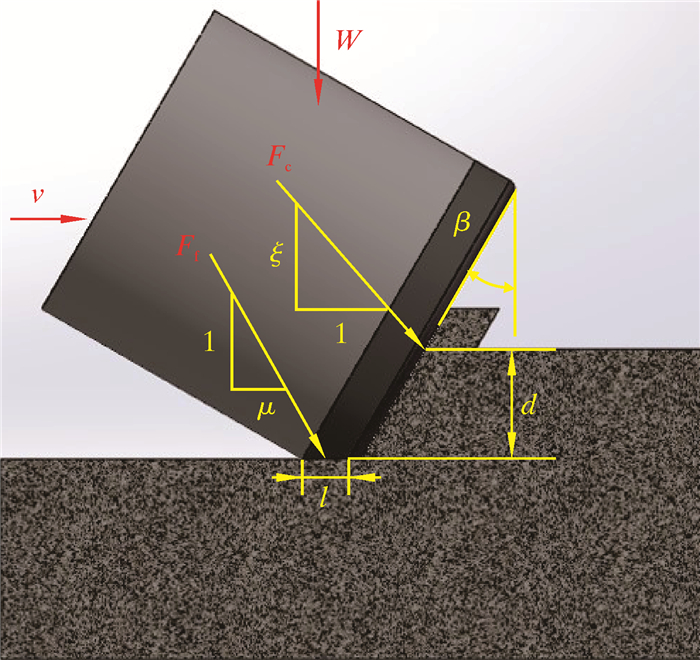
2 PDC钻头处“钻头-岩石”相互作用模型 2.1 PDC钻头处受力分析在钻进过程中,钻压施加在PDC钻头上端,使得钻头切入岩石内部,转盘的转动会带动PDC钻头切削岩石。从破岩角度分析,PDC钻头是整个钻进过程中关键的步骤,钻头和岩石之间的相互作用是造成扭转振动的主要原因。PDC单个切削齿与岩石之间相互作用示意图如图 2所示。
|
| 图 2 PDC单个切削齿与岩石之间相互作用示意图 Fig.2 Schematic diagram of interaction between single PDC cutter and rock |
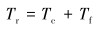
|
(5) |
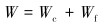
|
(6) |
其中:
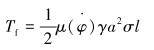
|
(7) |
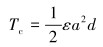
|
(8) |
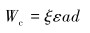
|
(9) |
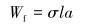
|
(10) |
式中:Tc为作用在切削方向上的力矩,N·m;Tf为作用在摩擦方向上的力矩,N·m;ξ表示切削面上钻压和扭矩之间的关系,与钻头的形状有关;σ为接触应力,MPa;l为摩擦面的长度,m;γ的取值范围为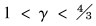
综合切削和摩擦部分,钻头处的阻力扭矩可以表示为:
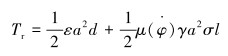
|
(11) |
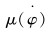
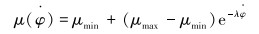
|
(12) |
式中:λ为衰减系数。
钻头和岩石之间的摩擦因数随着转速的增大而逐渐变小,在转速为0时(黏滞状态)的摩擦因数最大。
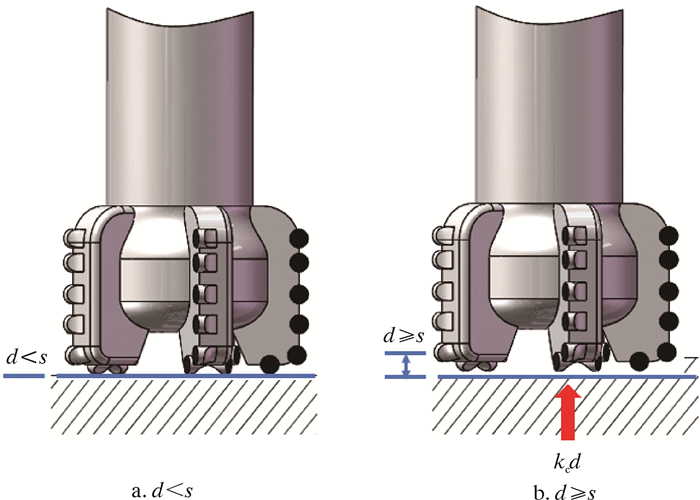
2.2 PDC钻头处钻压施加分析在钻进过程中,钻压是通过调节大钩的提拉力来控制,在PDC钻头处的钻压作用情况如图 3所示。
|
| 图 3 PDC钻头处钻压作用示意图 Fig.3 Schematic diagram of the WOB at the PDC bit |
图 3a表示的是PDC钻头刚好与井底岩石接触,为一种临界状态,此时PDC钻头没有对岩石产生压力,将此时钻杆的伸长量定义为一种临界长度s。图 3b表示的是静态平衡状态,此时PDC钻头压入岩石内部。
而实际钻进过程中,如果假定轴向没有振动,此时钻压值为:
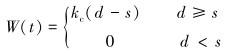
|
(13) |
式中:W(t)为钻头处的钻压,N;kc为岩石轴向刚度,N/m。
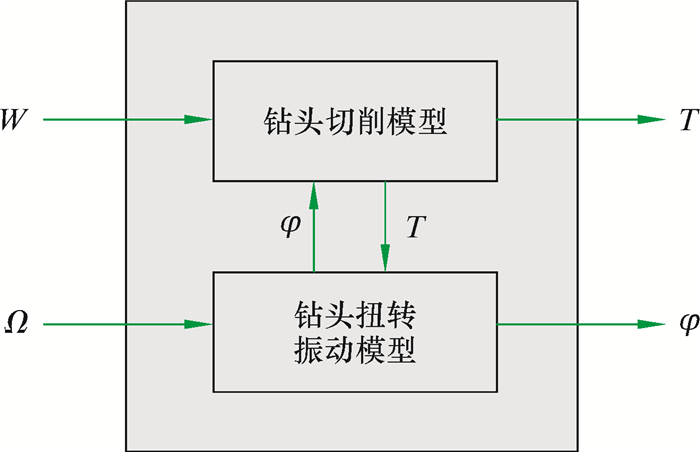
PDC钻头处钻压和扭矩之间的相互作用关系模型如图 4所示。
|
| 图 4 PDC钻头处钻压和扭矩之间的相互作用关系模型 Fig.4 Interaction relationship between WOB and torque at PDC bit |
由图 4可知,钻柱系统的输入能量来自于钻压W和转盘的转动Ω,系统的输出为钻头的转动,钻头处的切削模型和扭转振动模型相互耦合。钻头处的扭转振动模型会造成钻头转速的波动,而转速的波动会影响钻头处的受力。钻头切削岩石时钻头处扭矩的变化是造成钻头处扭转振动的主要原因,其值的变化直接影响钻头扭转振动的参数变化。
3 岩石硬度突增时PDC钻头处黏滑振动算例分析PDC钻头在钻进过程中,所受的扭矩和钻压与地层的性质直接相关。如果地层性质突变,使得公式(9)中kc的值发生改变,而大钩处的提拉力一定,钻杆的拉伸长度发生了改变,并最终改变了作用在PDC钻头处的压力,即钻压发生了改变。钻进过程中,地层由软地层突然进入硬地层,此时,kc值突然变大,岩石抵抗钻头切入的阻力增大,钻杆的拉伸长度缩短,钻头处的钻压突增,且钻头处的摩擦扭矩突增。
3.1 算例参数采用算例对模型进行求解。以一个典型的井深4 000 m的井作为算例进行分析,其参数如下:kT=743 N·m/rad,ka=0.58 MN/m,ε=50 MPa,c=4 N·s/rad,a=0.1 m,ξ=1,c1=1.35×10-8,c2=-1.9×10-4,kc=50 MN/m,F0=100 kN,μs=0.3,μd=0.35,lB=200 m,lp=3 800 m,dBe=0.228 6m,dBi=0.076 2 m,dPe=0.127 0 m,dPi=0.101 6 m,Ω=10.47 rad/s,F0=100 kN。
算例中,在前10 s所钻的地层为均质地层,在第10 s时所钻地层出现了突变,由软地层突然进入硬地层。笔者重点分析了以下两种情况,即变化后岩石性质分别为:①kc=80 MN/m;②kc=120 MN/m。
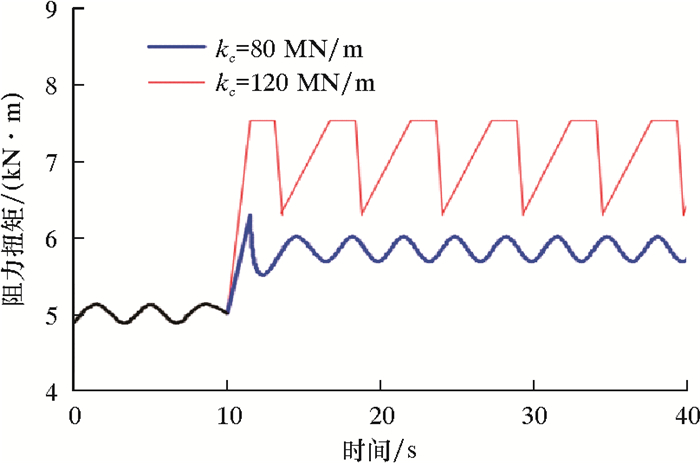
3.2 阻力扭矩和PDC钻头转速变化根据算例对以上模型进行计算,得出PDC钻头处的扭矩随时间的变化,如图 5所示。
|
| 图 5 PDC钻头处阻力扭矩随时间的变化图 Fig.5 Variation of resistant torque at PDC bit with time |
由图 5可知,PDC钻头处的扭矩在前10 s时围绕5 kN·m出现幅度为0.34 kN·m的往复波动。在情况①中,在10 s时,岩石硬度突变后,钻头处的扭矩突增并直接增大到最大值6.25 kN·m,在扭矩达到最大值后,又瞬间降低到5.67 kN·m,并最终围绕5.96 kN·m的扭矩出现幅度为0.29 kN·m的往复波动。
而在情况②中,在10 s时,钻头处的扭矩突增到7.57 kN·m,在扭矩达到最大值后,扭矩持续了1.21 s。之后,钻头处的扭矩发生了突减,瞬间降低到6.31 kN·m,在到达最小值后,又逐渐增大至7.57 kN·m。然后钻头处的扭矩依次出现往复波动。
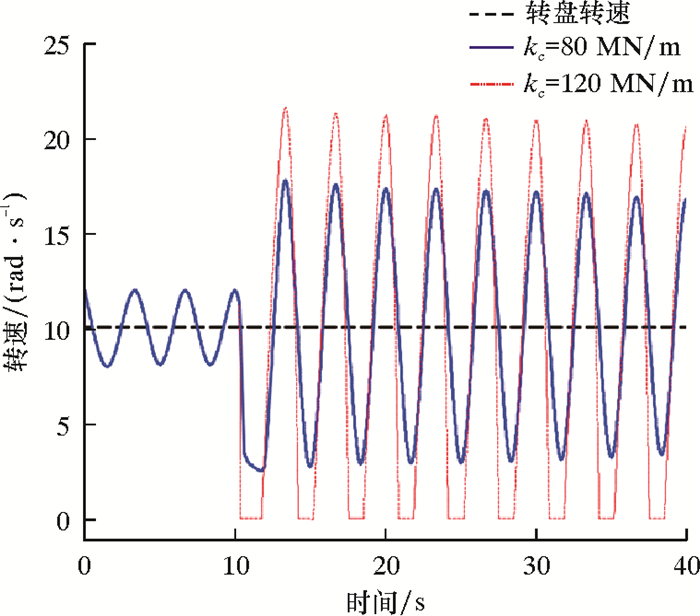
图 6为计算的以上两种情况下钻头处的转速随时间的变化曲线。由图 6可知,前10 s为钻头所钻地层的岩性没有发生改变的情况,钻头由于较小的初始扰动其转速发生了较小幅度的波动。
|
| 图 6 PDC钻头及转盘转速随时间的变化图 Fig.6 RPM of PDC bit and rotary table versus time |
图 6中红色曲线为情况①时PDC钻头的转速随时间的变化:在10 s时,钻头的转速由12.23 rad/s突然降低至2.67 rad/s,然后逐渐增大至17.21 rad/s,随后围绕10 rad/s出现往复波动,并随着时间推移振幅逐渐降低。从图 6还可以看出,钻头的转速出现了幅度较大的转速波动,但是没有出现钻头转速为0的状态,即没有出现黏滞的状态。图 6中蓝色曲线为情况②时PDC钻头的转速随时间的变化:在10 s时,钻头的转速由12.23 rad/s突然降至0 rad/s,即钻头停止转动,并持续1.21 s,随后逐渐增大至22.18 rad/s,并围绕10 rad/s出现往复波动,随着时间推移振幅逐渐降低。在情况②时,钻头出现了停止转动的状态,即出现了黏滑振动。
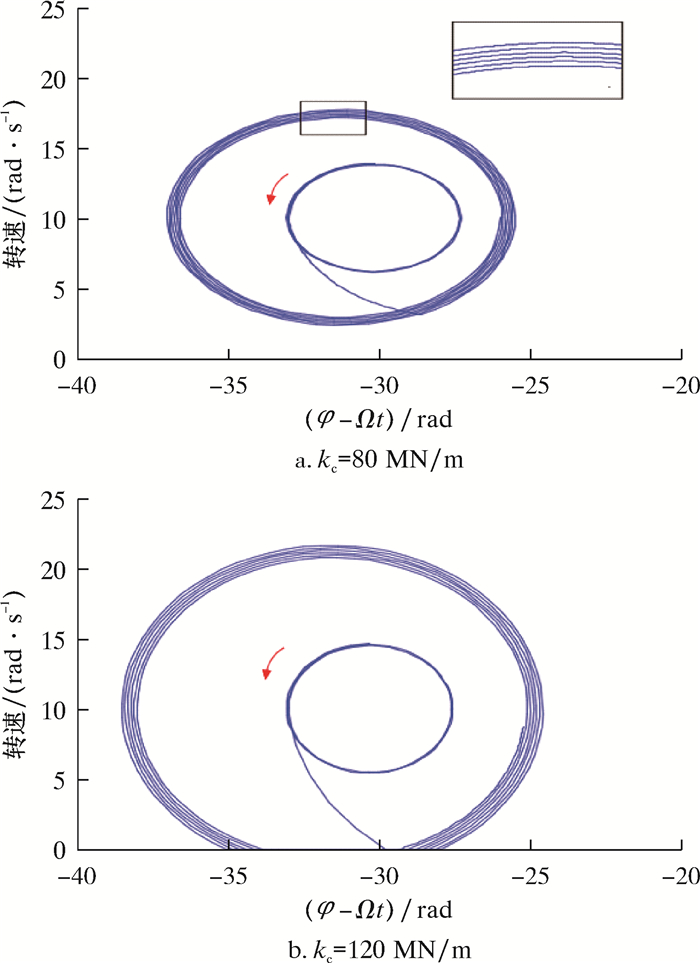
3.3 PDC钻头转速波动相位变化图 7为PDC钻头转速波动的相位图。
|
| 图 7 PDC钻头转速波动的相位图 Fig.7 Phase diagram of PDC bit RPM fluctuation |
图 7a为kc=80 MN/m时的相位图,横坐标为钻头转角与转盘转角之间的差值。由图 7可知,在开始状态时,其相位图为一个尺寸较小的椭圆。在岩性突变后,其相位图逐渐变化为一个尺寸较大的椭圆,其圆心向左发生偏移。PDC钻头和转盘处的相对角位移的最大值为-37.26 rad。
图 7b为kc=120 MN/m时的相位图。由图 7b可知,在岩性突变后,其相位图逐渐变化为一个尺寸较大的椭圆,且在下端出现转速为0的状态(图 7b中直线部分),此状态为黏滞状态。相对于最初的状态,在岩性突变后,其相位图的圆心向左发生了偏移。PDC钻头和转盘处的相对角位移的最大值为-38.85 rad。在黏滑振动过程中,钻头和转盘之间的相对角位移的最大值和最小值之间的差值约为7.5 rad。
根据仿真结果,在钻进过程中,当岩石的硬度突然增大后,作用在PDC钻头处的钻压会发生突然增大,钻头处的摩擦扭矩突然增大,钻头处阻力扭矩突增,使得钻头转速降低并出现扭转振动。钻头处扭转振动的幅值与突增后岩石硬度成正比,而一旦突增后的岩石硬度较大时,会出现钻头的黏滑振动,即钻头的转速突然降低至0,此时钻头处所受的摩擦力为静摩擦力。但是转盘依旧以一个恒定的转速转动,其传递的扭矩积累在PDC钻头处,当积聚的扭矩足以克服静摩擦扭矩,PDC钻头会以一个很大的加速度突然加速转动至最大转速,在加速过程中摩擦扭矩逐渐减小。在整个过程中,PDC钻头和岩石之间非线性的摩擦阻力不断发生改变,使得系统中耗散的总能量趋于输入的总能量,即摩擦扭矩的改变使得系统产生自激振动。
根据以上分析,在PDC钻头由软地层变化到硬地层时,当突变后的岩石硬度很大时,容易出现黏滑振动,需要采取一定的措施来抑制,例如降低钻压、提高转速和利用减振工具等方式,而且减振工具需要从钻头和岩石之间的相互作用作为出发点,即该类工具需要直接作用在PDC钻头处。
4 结论(1) 采用PDC钻头钻进时,当岩石硬度突增时,会使得PDC钻头扭转振动模型的系统参数发生改变,使得钻头处的转速发生波动,产生扭转振动;当所钻岩石岩性突变后的硬度较大,会出现PDC钻头的黏滑振动。一旦PDC钻头出现黏滑振动,其相轨迹为封闭的稳定的极限环。
(2) 岩性突变是造成PDC钻头黏滑振动的一个重要原因,而PDC钻头与岩石之间的非线性摩擦阻力是造成PDC钻头黏滑振动自激属性的根本原因。
(3) 为了延长PDC钻头的使用寿命,必须抑制地层变化过程中PDC钻头的黏滑振动。
| [1] |
FEAR M J, ABBASSIAN F, PARFITT S H I, et al. The destruction of PDC bits by severe slip-stick vibration[R]. SPE 37639-MS, 1997.
|
| [2] |
LEDGERWOOD L W, HOFFMANN O J, JAIN J R, et al. Downhole vibration measurement, monitoring and modeling reveal stick/slip as a primary cause of PDC-bit damage in today[R]. SPE 134488-MS, 2010.
|
| [3] |
田京燕, 徐玉超. 微心PDC钻头设计及现场试验[J]. 石油钻探技术, 2019, 47(1): 65-68. TIAN J Y, XU Y C. Design and field application of a micro-coring PDC bit[J]. Petroleum Drilling Techniques, 2019, 47(1): 65-68. |
| [4] |
李美求, 李嘉文, 李宁, 等. 周向冲击扭矩作用下PDC钻头的黏滑振动分析[J]. 石油钻采工艺, 2018, 40(3): 287-292. LI M Q, LI J W, LI N, et al. Analysis on the stick-slip vibration of PDC bit under the effect of circumferential torque impact[J]. Oil Drilling & Production Technology, 2018, 40(3): 287-292. |
| [5] |
HUANG G L, HAN Z Y. Mechanism analysis on torsional stick-slip vibration of drillstring in extended reach well and some ways to its suppression[J]. Petroleum Drilling Techniques, 2001, 29(2): 4-6. |
| [6] |
RICHARD T, GERMAY C, DETOUMAY E. A simplified model to explore the root cause of stick-slip vibrations in drilling systems with drag bits[J]. Journal of Sound and Vibration, 2007, 305(3): 432-456. DOI:10.1016/j.jsv.2007.04.015 |
| [7] |
BESSELINK B, VAN DE WOUW N, NIJMEIJER H. A semianalytical study of stick-slip oscillations in drilling systems[J]. Journal of Computational and Nonlinear Dynamics, 2011, 6(2): 21006-21014. DOI:10.1115/1.4002386 |
| [8] |
LIN Y Q. Stick-slip vibration of drill strings[J]. Journal of Manufacturing Science and Engineering, 1991, 113(1): 38-43. DOI:10.1115/1.2899620 |
| [9] |
GERMAY C, DENOEL V, DETOVRNAY E. Multiple mode analysis of the self-excited vibrations of rotary drilling systems[J]. Journal of Sound and Vibration, 2009, 325(1/2): 362-381. |
| [10] |
祝效华, 汤历平, 童华. 高频扭转冲击钻进的减振与提速机理研究[J]. 振动与冲击, 2012, 31(20): 75-78. ZHU X H, TANG L P, TONG H. Rock breaking mechanism of a high frequency torsional impact drilling[J]. Journal of Vibration and Shock, 2012, 31(20): 75-78. |
| [11] |
韩春杰, 阎铁. 大位移井钻柱"粘滞-滑动"规律研究[J]. 天然气工业, 2004, 24(11): 58-60. HAN C J, YAN T. Research on the "sticking-slipping" law of drillstring in extended-reach well[J]. Natural Gas Industry, 2004, 24(11): 58-60. |
| [12] |
SILVEIRA M, WIERCIGROCH M. Low dimensional models for stick-slip vibration of drill-strings[J]. Journal of Physics:Conference Series, 2009, 181(1): 12-56. |
| [13] |
付蒙, 李江红, 吴亚锋, 等. 钻柱黏滑振动特性仿真与产生机理分析[J]. 西北工业大学学报, 2016, 34(3): 467-472. FU M, LI J H, WU Y F, et al. Characteristic simulation and mechanisms analysis for drill-strings stick-slip vibration[J]. Journal of Northwestern Polytechnical University, 2016, 34(3): 467-472. |
| [14] |
JANSEN J D, VAN DEN STEEN L. Active damping of self-excited torsional vibration vibrations in oilwell drillstrings[J]. Journal of Sound and Vibration, 1995, 179(4): 647-668. DOI:10.1006/jsvi.1995.0042 |
| [15] |
YIGIT A S, CHRISTOFOROU A P. Coupled torsional and bending vibrations of actively controlled drillstrings[J]. Journal of Sound and Vibration, 2000, 234(1): 67-83. |
| [16] |
RICHARD T, DETOUMAY E, FEAR M, et al. Influence of bit-rock interaction on stick-slip vibrations of PDC bits[R]. SPE 77616, 2002.
|
| [17] |
ULF JAKOB F A, VAN DE WOUW N. Dynamics of a distributed drill string system:Characteristic parameters and stability maps[J]. Journal of Sound and Vibration, 2018, 417: 376-412. DOI:10.1016/j.jsv.2017.12.002 |
| [18] |
BAKHTIARI-NEJAD F, HOSSEINZSDEH A. Nonlinear dynamic stability analysis of the coupled axial-torsional motion of the rotary drilling considering the effect of axial rigid-body dynamics[J]. International Journal of Non-Linear Mechanics, 2017, 88: 85-96. DOI:10.1016/j.ijnonlinmec.2016.10.011 |


