2. 中国石油大学(北京)
2. China University of Petroleum(Beijing)
0 引言
套管腐蚀损坏是酸性油气田开发过程中存在的重要问题,也是影响井筒完整性的主要形式之一。一般而言,油气田在开发设计阶段会根据井下CO2/H2S的分压采用防腐材质,但在实际生产过程中,储层油气组分发生变化后经常导致腐蚀的发生,套管腐蚀后其剩余强度随之降低,严重影响油气井的生产安全。因此,开展套管腐蚀后剩余强度预测,对于评估油气井井筒完整性及后续增产改造可行性具有重要意义和实用价值。
近几年关于套管腐蚀的研究较多,李文飞等[1]采用数值方法研究了含单一圆弧形腐蚀套管的剩余强度。石晓兵等[2]应用弹塑性理论研究了点蚀后套管剩余强度的变化规律。闫相祯等[3]研究了腐蚀孔引起的应力集中对套管强度的影响。张智等[4]分析了均匀腐蚀和点蚀后温度、内压对套管等效应力的影响。许志倩等[5]研究了套管在均匀、点状和裂缝性腐蚀缺陷下的剩余强度。这些研究都未考虑套管表面腐蚀坑形状、尺寸以及多腐蚀坑对剩余强度的影响,而在实际生产过程中,套管腐蚀后其表面腐蚀坑形状各异且大多呈多点局部腐蚀[6]。
针对上述问题,本文基于对套管表面腐蚀坑形状的规则化表征,采用有限元法建立了可模拟不同形状腐蚀缺陷的套管力学分析模型,用弹塑性理论进行腐蚀后剩余抗内压和抗外挤强度求解。以直径244.5 mm、P110钢级套管为例,对圆球、椭球和矩体等3种形状、不同几何尺寸腐蚀坑的套管剩余强度进行研究,给出了套管腐蚀后剩余强度预测流程,并成功应用于海外M油田在生产井。基于该井的MIT套管腐蚀检测结果,将本文方法预测的剩余强度与个别点的试验数据进行对比,精度达到89%以上,验证了本文方法的合理性与实用性。
1 模型建立 1.1 腐蚀缺陷规则化表征套管腐蚀一般可分为均匀腐蚀和局部点蚀[7]。均匀腐蚀可视为套管壁厚随着腐蚀的发生均匀减薄,剩余强度可采用API公式计算,不作为本文研究重点。而对于局部腐蚀,由于真实的腐蚀缺陷很不规则,所以需要对其进行规则化表征。本文借鉴石油工业油气输送管道与压力容器的腐蚀形状规则化处理一般推荐做法[8],对套管局部腐蚀坑按照以下规则进行表征。
1.1.1 单个凹坑缺陷的表征(见图 1)
|
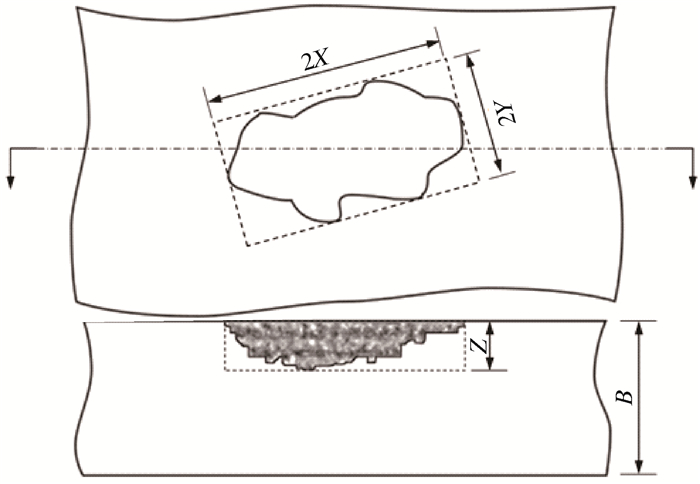
| 图 1 单个凹坑缺陷表征示意图 Fig.1 Schematic diagram of single pit characterization |
单一不规则凹坑缺陷可根据外接矩形的长宽比规则化为圆球、椭球或矩体。当长宽比λ等于1时,可表征为圆球腐蚀坑;当1<λ≤5时,可表征为椭球腐蚀坑,长轴2X即为外接矩形的长,短轴2Y为平行于长轴且与凹坑边缘相切的两条直线间的距离;当λ大于5时,可表征为矩体腐蚀坑。圆球、椭球及矩体坑的深度为腐蚀坑的最大深度Z。
1.1.2 多个凹坑缺陷的表征(见图 2)
|
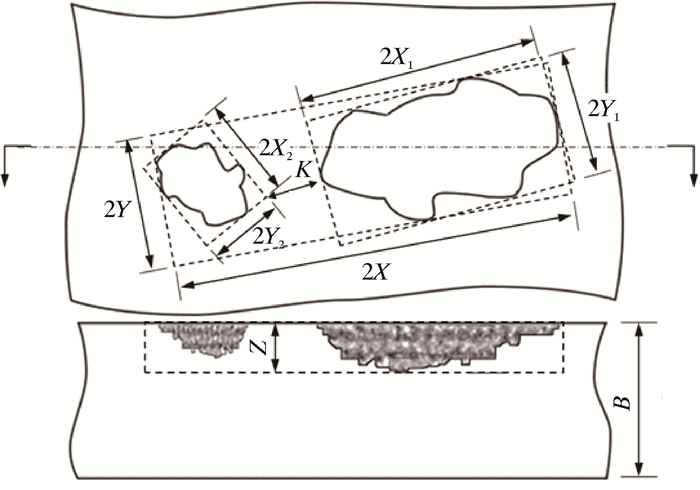
| 图 2 多个凹坑缺陷表征示意图 Fig.2 Schematic diagram of multiple pits characterization |
当存在两个以上的凹坑时,应分别按单个凹坑进行规则化并确定各自的凹坑长宽比λ。若规则化后相邻两凹坑边缘最小距离K大于较小凹坑的长边,则可将两个凹坑视为互相独立的单个凹坑分别进行评定,否则,应将两个凹坑合并为一个凹坑来进行评定。该凹坑的长为两个凹坑外侧边缘之间的最大距离,宽为平行于长轴且与两个凹坑外侧边缘相切的任意两条直线之间的最大距离,然后再按照单个凹坑缺陷来表征。
1.2 几何模型为预测局部腐蚀后套管剩余强度,需要根据井下腐蚀程度检测结果和腐蚀坑的规则化表征建立可用于数值分析的几何模型。按照1.1节中的表征规则,首先建立套管三维几何模型,再建立圆球、椭球或矩体腐蚀坑,利用摩尔减法运算,实现套管内壁腐蚀坑的模拟。腐蚀坑大小由圆球半径R、椭球长短轴、矩体长宽以及腐蚀深度比确定。腐蚀深度比r定义为:圆球、椭球或矩体与套管内壁相交后,圆球、椭球或矩体进入套管的深度与套管原始壁厚t之比。
1.3 有限元模型为研究不同腐蚀坑形状、尺寸及腐蚀坑个数对套管剩余强度的影响,采用ANSYS中的Solid45八节点三维实体单元进行单位长度腐蚀套管的实体建模。该分析单元具有塑性、蠕变、膨胀、应力强化、大变形和大应变属性,在保证精度的前提下,具有良好的收敛性,且分析结果不会受体积锁死(由塑性或其他不可压缩性引起)的影响。有限元分析套管建模采用的基本参数见表 1。
| 直径/mm | 壁厚/mm | 抗内压强度/MPa | 抗外挤强度/MPa | 屈服强度/MPa | 弹性模量/GPa | 泊松比 |
| 244.5 | 12.0 | 65.1 | 36.5 | 758.0 | 210 | 0.3 |
对于腐蚀坑的敏感性模拟,考虑以下工况。
(1) 圆球腐蚀坑:圆球半径为1~8倍套管壁厚,腐蚀深度比为0~95%,腐蚀坑1~12个沿套管内壁环向分布;
(2) 椭球腐蚀坑:长短轴比为1~10,短轴为3倍套管壁厚,腐蚀深度比为0~95%,腐蚀坑1~9个沿套管环向和轴向分布;
(3) 矩体腐蚀坑:单个矩体腐蚀坑沿套管环向的边长考虑0.5°~90.0°圆心角的不同弧形边长分布,沿套管轴向边长考虑1~50倍套管壁厚的长度分布,腐蚀深度比为0~95%。
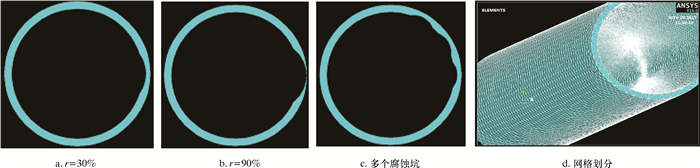
根据以上参数,建立有限元模型(以圆球形腐蚀坑为例),如图 3所示。
|
| 图 3 圆球形腐蚀坑有限元分析模型 Fig.3 Finite element analysis model of spherical corrosion pit |
1.4 套管剩余强度计算准则
当结构中任意一点的应力达到屈服强度或允许的强度极限值时,结构失效。根据第四强度理论,将Von Mises等效应力屈服准则作为套管屈服准则,等效应力σi的表达式如下:
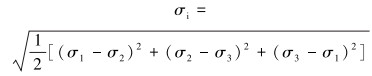
|
(1) |
式中:σ1、σ2、σ3分别表示套管3个方向的主应力,MPa。
根据弹塑性力学基本理论,当给定外径、壁厚、弹性模量和泊松比的套管受内压或外压作用时,在线弹性和小变形范围内,其最大等效应力σimax与内压或外压p之比是一个无量纲常数k,也就是:
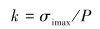
|
(2) |
因此,在套管腐蚀后剩余强度求解时,利用单位载荷先求解出结构最大等效应力及无量纲常数k,再根据套管的屈服强度σs与无量纲常数k,得到剩余强度Pr,即:
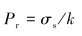
|
(3) |
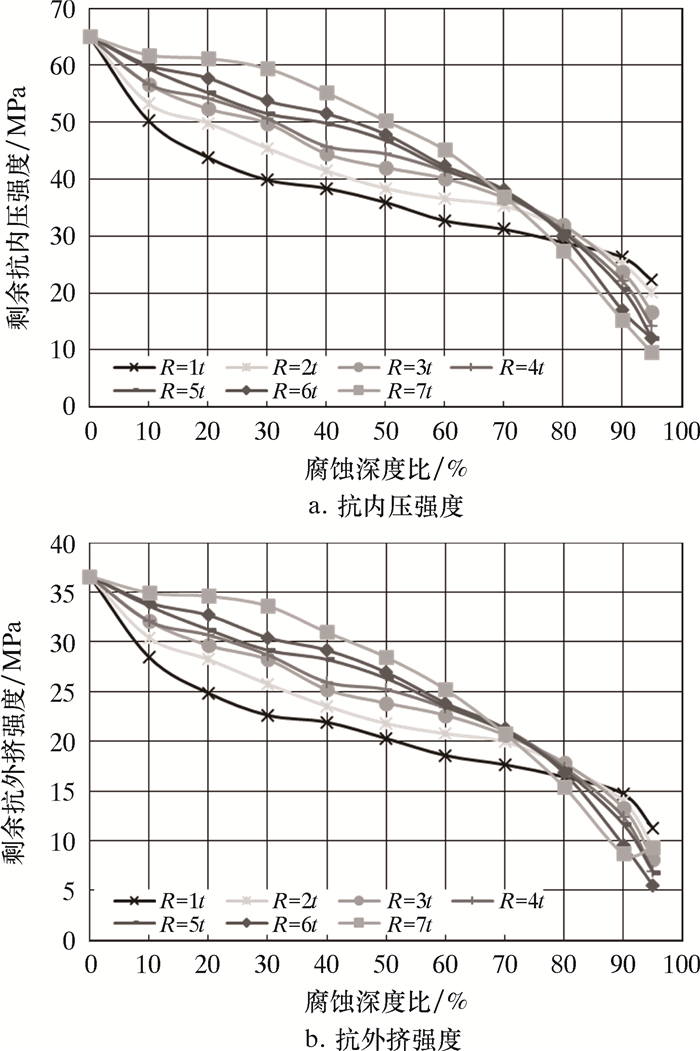
不同圆球半径及不同腐蚀深度比对套管剩余强度的影响规律如图 4所示。
|
| 图 4 不同圆球半径及不同腐蚀深度比对套管剩余强度的影响规律 Fig.4 Effect of different sphere radius and corrosion depth ratio on residual strength of casing |
由图 4可知:在单一圆球形腐蚀坑影响下,套管剩余强度随腐蚀深度比的变化规律近似呈6次多项式关系,且关系曲线中存在明显拐点,拐点值随圆球半径(即圆球大小)的增大逐渐减小;当腐蚀深度比小于拐点值时,圆球半径越小,套管剩余强度下降幅度越快,其主要原因是小圆球相对于大圆球而言,应力集中更明显,例如,当腐蚀深度比为30%时,圆球半径为1倍套管壁厚比5倍套管壁厚的剩余抗内压强度小22%;当腐蚀深度比大于拐点值时,圆球半径越小,套管剩余强度下降幅度反而变缓,其主要原因是圆球形腐蚀坑半径越大,在腐蚀深度比较大的情况下,同时处于应力强度极值的面积增大导致了其整体强度更低。
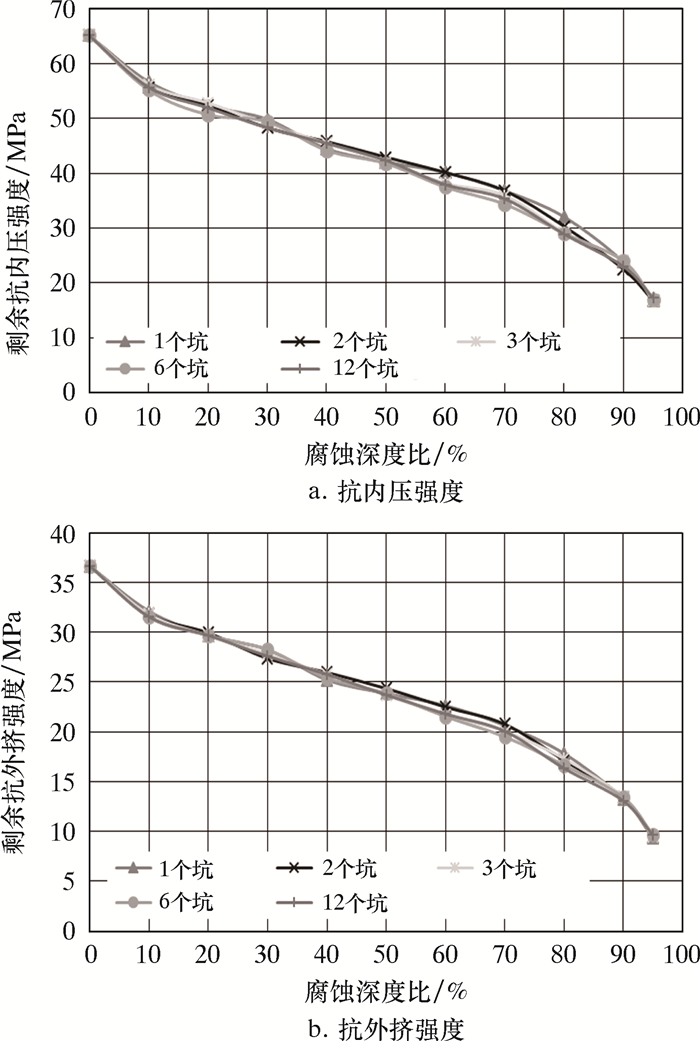
多个圆球形腐蚀坑对套管剩余强度的影响规律如图 5所示。分析发现,在套管钢材和受力状态相同的情况下,最大应力为某个腐蚀坑位置的应力,与腐蚀坑的个数无关。因此,腐蚀坑个数对套管最大应力及剩余强度的影响不明显,但同时处于最大应力的分布面积增大,并且随着腐蚀坑的增加,套管破坏受多点控制。
|
| 图 5 多个圆球形腐蚀坑对套管剩余强度的影响规律 Fig.5 Effect of multiple spherical corrosion pits on residual strength of casing |
2.2 椭球形腐蚀坑对套管剩余强度的影响
不同长/短轴及不同腐蚀深度比椭球形腐蚀坑对套管剩余强度的影响规律如图 6所示。由图 6可知:在单一椭球形腐蚀坑工况下,套管剩余强度随腐蚀坑深度比增加呈下降趋势,近似符合线性规律,转化点不明显;随着长/短轴比的增加,剩余强度降低,但相对变化不明显。

|
| 图 6 不同长/短轴及不同腐蚀深度比椭球形腐蚀坑对套管剩余强度的影响规律 Fig.6 Effect of different X/Y and different corrosion depths ratio of the single ellipsoidal corrosion pit on the residual strength of casing |
分析多个椭球形腐蚀坑对套管剩余强度的影响规律,并将分析结果与单个椭球形腐蚀坑分析结果进行对比,得出与圆球形腐蚀坑相同的结论:椭球形腐蚀坑个数对套管最大应力及剩余强度影响不明显,但随着腐蚀坑的增加,套管破坏受多点控制。
2.3 矩体形腐蚀坑对套管剩余强度的影响针对矩体形腐蚀坑,模拟了以下工况:单个矩体形腐蚀坑沿套管环向的长度考虑0.5°~90.0°圆心角的弧长分布,沿套管轴向的长度考虑1~50倍套管壁厚的长度分布,腐蚀深度比为0~95%。模拟结果表明:在单一矩体腐蚀坑工况下,套管剩余强度随腐蚀坑深度呈下降趋势,初期下降幅度明显;随矩体轴向长度增加,剩余强度降低,但变化不大;随矩体环向长度增加,剩余强度变化不大,在极小的环向长度工况下(近似裂缝形腐蚀)剩余强度急剧降低。多个矩体腐蚀坑与圆球形和椭球形腐蚀规律相同。
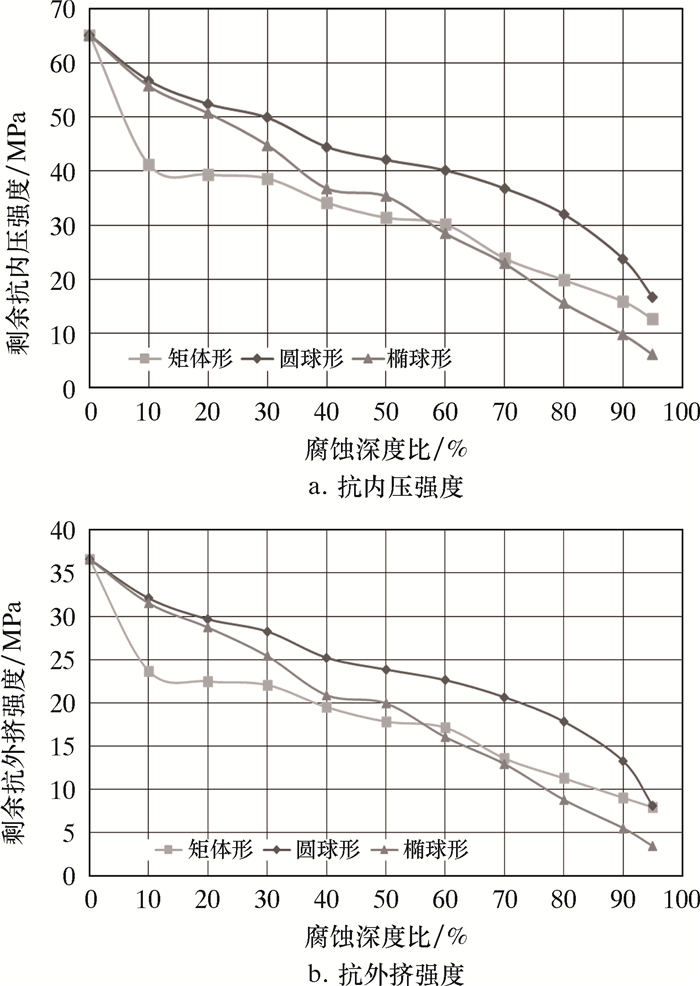
2.4 不同腐蚀坑形状影响对比通过对圆球形、椭球形及矩体形等不同腐蚀坑形状和大小、腐蚀深度比以及不同腐蚀坑个数的敏感性分析,可以得出:当腐蚀坑投影面积相同时,3种形状腐蚀坑对套管剩余强度的影响规律如图 7所示。从图 7可以看出,矩体形腐蚀对套管剩余强度的影响最严重,椭球形腐蚀影响程度次之,圆球形腐蚀影响程度最低,最大相差65%。
|
| 图 7 不同腐蚀坑形状对套管剩余强度的影响规律 Fig.7 Effect of different corrosion pit shapes on residual strength of casing |
2.5 套管剩余强度预测流程
通过对套管局部腐蚀坑的规则化表征以及不同腐蚀坑的敏感性分析,得到了含腐蚀缺陷套管剩余强度的变化规律。对于一口在生产井,其套管剩余强度预测步骤如下:①利用套管腐蚀检测测井,得到沿井深剖面的套管腐蚀坑形状成像数据;②基于腐蚀缺陷表征规则,将测得的套管内壁腐蚀坑进行规则化表征,形成沿井深剖面最危险腐蚀数据;③利用有限元对目标套管腐蚀进行敏感性分析,其敏感性分析数据应涵盖经表征后的腐蚀坑几何尺寸;④对敏感性分析结果进行回归处理,得到不同腐蚀坑形状、大小对应的套管抗内压和抗外挤强度关系式;⑤将回归结果代入步骤②,得到沿井深剖面的套管剩余强度。
3 应用实例以海外M油田的M-1井为例,该井生产套管外径168.3 mm,壁厚10.6 mm,钢级C75。生产过程中,油气组分里出现了之前未预测到的CO2,并造成了套管腐蚀。2017年实施MIT腐蚀测井,得到了沿井深剖面的腐蚀形状及程度的成像测井资料。根据套管腐蚀测井资料,利用建立的方法和流程进行套管剩余强度预测,并将预测结果与个别井深位置的套管剩余强度试验测定值进行对比,两者重合度达到89%以上,满足工程设计要求。套管剩余强度预测值与试验值部分数据见表 2。表 2中,H为井深,P1、P1s为剩余抗内压强度预测值和试验值,P2、P2s为剩余抗外挤强度预测值和试验值,δ1、δ2为剩余抗内压强度和剩余抗外挤强度预测精度。
| H/m | P1/MPa | P2/MPa | P1s/MPa | P2s/MPa | δ1/% | δ2/% |
| 3 503 | 53.75 | 52.07 | ||||
| 3 515 | 53.55 | 51.78 | ||||
| 3 527 | 54.82 | 53.30 | 57.02 | 51.31 | 96.1 | 96.3 |
| 3 539 | 53.55 | 51.77 | ||||
| 3 551 | 54.02 | 53.18 | ||||
| 3 563 | 54.37 | 53.30 | ||||
| 3 575 | 54.37 | 52.60 | ||||
| 3 588 | 54.37 | 52.71 | 58.23 | 47.24 | 93.4 | 89.6 |
| 3 599 | 53.15 | 48.56 | ||||
| 3 611 | 54.02 | 53.18 | ||||
| 3 623 | 54.82 | 53.41 | ||||
| 3 633 | 54.82 | 53.41 | 57.58 | 48.78 | 95.2 | 91.3 |
| 3 645 | 54.37 | 53.30 | ||||
| 3 657 | 54.82 | 53.41 | ||||
| 3 669 | 53.40 | 45.81 | ||||
| 3 680 | 54.37 | 52.05 |
4 结论
(1) 建立了一种基于套管腐蚀坑规则化表征的有限元法预测剩余强度方法和具体流程,结合测井可有效预测含不同腐蚀缺陷形状的套管剩余强度。
(2) 腐蚀坑深度比是影响套管剩余强度的主要因素;当腐蚀坑投影面积相同时,矩体形坑腐蚀对套管剩余强度的影响最严重,椭球形腐蚀坑次之,圆球形腐蚀坑影响程度最低;对于相同的腐蚀形状及尺寸,腐蚀坑个数对套管剩余强度极值影响较小,但套管损坏或屈服的危险点增加。
(3) 通过实例验证,本文建立的预测方法精度可达89%以上,这对于评估在生产井的套管完整性及其再利用具有重要的指导意义。
| [1] |
李文飞, 李玄烨, 夏文安. 腐蚀套管剩余强度数值模拟分析[J]. 天然气与石油, 2013, 31(6): 70-75. LI W F, LI X Y, XIA W A. Numerical simulation analysis on corroded casing residual strength[J]. Natural Gas and Oil, 2013, 31(6): 70-75. DOI:10.3969/j.issn.1006-5539.2013.06.020 |
| [2] |
石晓兵, 陈平, 徐进, 等. 油气井套管CO2点状腐蚀剩余强度分析[J]. 天然气工业, 2006, 26(2): 95-97. SHI X B, CHEN P, XU J, et al. Analysis on residual strength of CO2 tubercular corrosion for casings of oil/gas wells[J]. Natural Gas Industry, 2006, 26(2): 95-97. DOI:10.3321/j.issn:1000-0976.2006.02.029 |
| [3] |
闫相祯, 张殿锋, 杨秀娟, 等. 表面缺陷深度对套管强度影响规律数值模拟研究[J]. 石油矿场机械, 2009, 38(11): 1-4. YAN X Z, ZHANG D F, YANG X J, et al. Study on strength reduction of casing with surface defects[J]. Oil Field Equipment, 2009, 38(11): 1-4. DOI:10.3969/j.issn.1001-3482.2009.11.001 |
| [4] |
张智, 孔维伟, 刘志伟, 等. 腐蚀缺陷套管的剩余强度研究[J]. 中国科技论文, 2016, 11(21): 2467-2472. ZHANG Z, KONG W W, LIU Z W, et al. Study on residual strength of corrosion defect casing[J]. China Sciencepaper, 2016, 11(21): 2467-2472. DOI:10.3969/j.issn.2095-2783.2016.21.013 |
| [5] |
许志倩, 闫相祯, 杨秀娟, 等. 不同缺陷对套管剩余强度影响分析[J]. 机械设计, 2014, 31(8): 74-78. XU Z Q, YAN X Z, YANG X J, et al. Different defects impact analysis on casing residual strength[J]. Journal of Machine Design, 2014, 31(8): 74-78. DOI:10.3969/j.issn.2095-509X.2014.08.018 |
| [6] |
张西明, 李军, 张新发, 等. 长庆油田小套管的腐蚀与防护[J]. 腐蚀科学与防护技术, 2004, 16(1): 59-61. ZHANG X M, LI J, ZHANG X F, et al. Corrosion and protection for small-casings in Changqing Oilfield[J]. Corrosion Science and Technology Protection, 2004, 16(1): 59-61. DOI:10.3969/j.issn.1002-6495.2004.01.018 |
| [7] |
毛克伟, 史茂成. 油气井套管腐蚀原因与防腐措施[J]. 石油钻探技术, 1996, 24(1): 31-36. MAO K W, SHI M C. Cause and prevention of casing corrosion in oilwells[J]. Petroleum Drilling Techniques, 1996, 24(1): 31-36. |
| [8] |
石油管材专业标准化技术委员会.含缺陷油气输送管道剩余强度评价方法: SY/T 6477-2014[S].北京: 石油工业出版社, 2015. Petroleum Pipe Professional Standardizatrion Technical Committee. Evaluation methods of remaining strength for oil & gas transmission pipeline with flaws: SY/T 6477-2014[S]. Beijing: Petroleum Industry Press, 2015. |


