2. 中国石油大学(华东)机电工程学院
2. College of Mechanical and Electronic Engineering, China University of Petroleum(Huadong)
0 引言
传统的钢制抽油杆作业不连续,作业周期较长,且需要接箍连接,接箍的活塞效应会增加地面能耗,同时,接箍的尺寸大于抽油杆,更易与油管产生偏磨。碳纤维连续抽油杆(以下简称碳纤维抽油杆)以其强度高、密度小及抗腐蚀等优势逐渐应用到油田开采[1-2]中。美国于20世纪80年代首次应用,我国进入21世纪后才开始对碳纤维抽油杆进行研究应用[3-4]。由于碳纤维抽油杆为柔性杆,底部不能受压,一般在使用时下端接加重钢杆组成混合杆柱进行使用。对于抽油杆运动的研究,自1963年S.G.GIBBS[5]针对理想直井提出一维波动方程,对抽油杆振动的研究进入理论分析阶段,之后考虑更多因素的改进模型[6-7]随之建立。2013年刘芳超等[8]采用有限元数值模拟方法,分析了单级钢抽油杆柱在不同简化激励下柱塞的位移规律。大量学者从共振的角度出发,对柔性抽油杆的柱塞超冲程进行了定性解释。
由于碳杆弹性性能的影响,碳纤维抽油杆在使用时柱塞存在超冲程现象,即柱塞的冲程高于悬点冲程与冲程损失的差值,对碳纤维抽油杆的设计和使用产生一定的影响,然而柱塞的有效冲程与产液量和系统效率均有密切关系,从机理上分析碳纤维钢混合抽油杆柱塞的运动规律,进而得到量化结果十分必要。对此,笔者基于系统相应理论,根据系统的激励类型进行分析,将抽油杆振动的激励类别分解成两个子运动,并建立其数学模型。依据此模型,分析得到冲次对混合杆柱柱塞有效位移及不同激励下柱塞超冲程的影响规律。同时对比分析了全钢杆和混合杆柱柱塞运动规律的不同。研究结果可为现场合理设计使用碳纤维抽油杆提供理论依据。
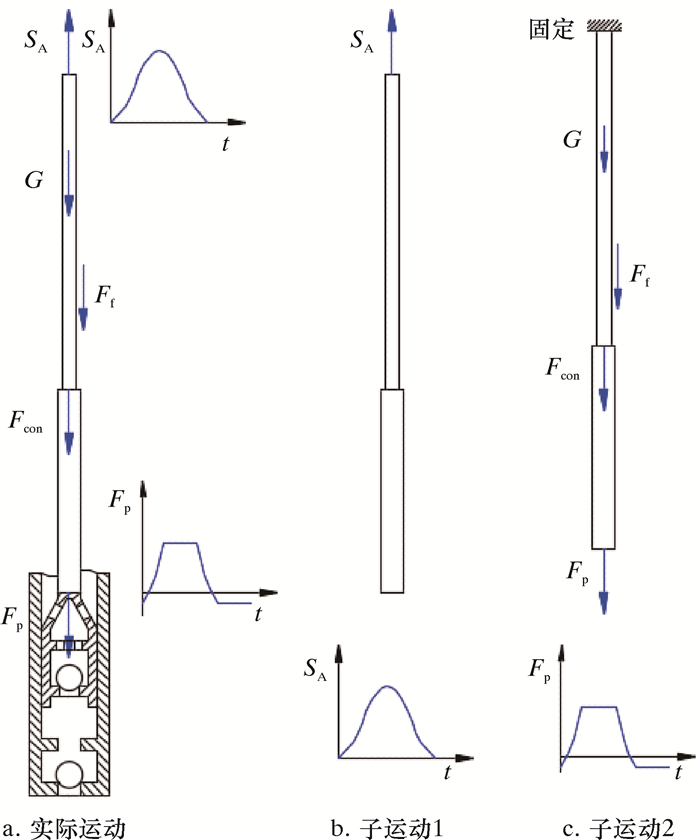
1 抽油杆柱运动分解抽油杆柱的运动分解如图 1所示。
|
| 图 1 抽油杆柱运动分解 Fig.1 Motion decomposition of sucker rod string |
抽油杆柱受力有杆柱自重G、摩阻Ff(包括杆管摩擦和杆液摩阻)、接头变截面作用力Fcon和泵载荷Fp。悬点位移激励为SA。泵载荷是变量,可作为一个新的激励。因此根据激励方式将抽油杆柱的运动分解为由悬点位移激励产生的振动和有泵载荷时变性引起的杆柱振动,前者杆柱的位移场函数为u1(s, t),后者杆柱的位移场函数为u2(s, t)。子运动1只受悬点位移激励,底端自由。子运动2杆柱顶部固定,杆柱承受G、Ff、Fcon和Fp。
2 抽油杆柱数学模型 2.1 波动方程 2.1.1 抽油杆运动方程[9]抽油杆运动方程为:
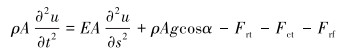
|
(1) |
式中:u为抽油杆单元节点位移,m;ρ为抽油杆材料密度,kg/m3;A为抽油杆截面面积,m2;g为重力加速度,m/s2;Frt为油管对单位长度抽油杆摩阻力,N;Fct为油管对接箍摩阻力,N;Frf 为井液对单位长度抽油杆摩阻力,N;α为井斜角,(°);t为时间,s;s为节点位置,m。
2.1.2 边界条件上边界条件为[10]:
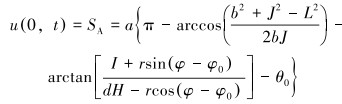
|
(2) |
式中:SA为游梁式抽油机悬点位移,m;a为抽油机游梁前臂长度,m;b为抽油机游梁后臂长度,m;L为连杆长度,m;r为曲柄长度,m;I为曲柄回转中心与游梁回转中心之间的水平距离,m;dH为曲柄回转中心与游梁回转中心之间的竖直距离,m;θ0悬点在下死点时,游梁后臂与竖直方向的夹角,(°);φ0为悬点在下死点时,曲柄与竖直方向的角,(°)。
变截面处边界条件为:
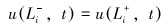
|
(3) |
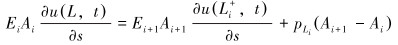
|
(4) |
式中:Ei和Ei+1分别为第i级和第i+1级抽油杆弹性模量,Pa;Ai和Ai+1分别为第i级和第i+1级抽油杆截面面积,m2;pLi为变截面处井液压力,Pa;Li为变截面处位置,m,上标“+”和“-”代表方向,分别为向下和向上。
下边界条件包括上冲程、下冲程和泵筒内压力。
上冲程:
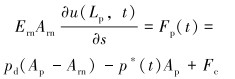
|
(5) |
式中:Ern为最后一级抽油杆弹性模量,Pa;Arn为最后一级抽油杆截面面积,m2;pd为抽油泵排出压力,Pa;p*为抽油泵泵筒内压力,Pa;Ap为柱塞截面面积,m2;Fc为泵筒与柱塞之间的摩擦力,N。
下冲程:
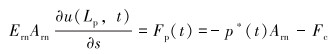
|
(6) |
泵筒内压力为:
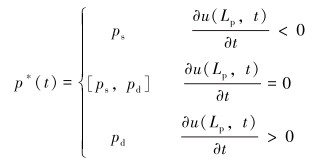
|
(7) |
式中:ps为抽油泵入口压力,Pa。
2.1.3 初始条件以下冲程结束为初始时刻,固定阀和游动阀均关闭,泵筒内压力为排出压力。初始位移为:
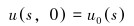
|
(8) |
式中:u0为泵筒压力等于pd时抽油杆柱的悬垂位移,m。
初始速度为:
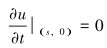
|
(9) |
抽油杆柱运动模型:
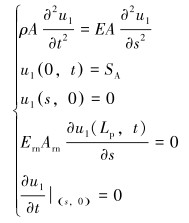
|
(10) |
式中:u1为悬点位移激励下的抽油杆柱位移,m。
变截面处边界条件如下:
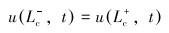
|
(11) |
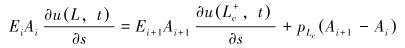
|
(12) |
式中:Lc为碳纤维抽油杆底端深度,m。
2.3 泵时变载荷激励运动数学模型抽油杆柱运动模型:
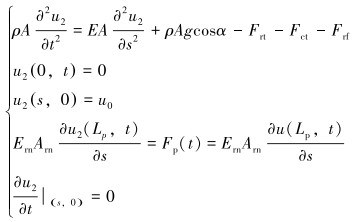
|
(13) |
式中:u2为泵时变载荷激励下的抽油杆柱位移,m。
变截面处边界条件如下:
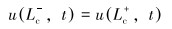
|
(14) |
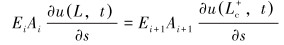
|
(15) |
波动方程采用有限差分法进行求解,可以得到抽油杆柱整体的运动位移场u(s,t)。悬点激励运动数学模型求解可得抽油杆柱分位移场u1(s,t)。泵时变载荷激励运动数学模型的底边界条件,即泵时变载荷未知,采用波动方程求解的泵载荷作为泵时变载荷激励运动数学模型的底边界条件进行求解,可得抽油杆柱分位移场u2(s,t)。
3 实例验证以临盘LP10-7井为例,对抽油杆柱的运动进行仿真分析。油井基本参数如表 1所示。
| 参数名称 | 数值 |
| 泵径/mm | 38 |
| 泵挂/m | 2 580 |
| 碳杆直径/mm | 19 |
| 碳杆密度/(kg·m-3) | 1 960 |
| 碳杆弹性模量/GPa | 95 |
| 钢杆直径/mm | 22 |
| 钢杆密度/(kg·m-3) | 7 950 |
| 钢杆弹性模量/GPa | 211 |
| 碳杆占比 | 0.49 |
| 油管内径/mm | 62 |
| 井液密度/(kg·m-3) | 900 |
| 含水体积分数/% | 80 |
| 油压/MPa | 0.2 |
| 套压/MPa | 0.3 |
| 生产油气比/(m3·m-3) | 0 |
| 井液动力黏度/(mPa·s) | 20 |
| 冲程/m | 4.8 |
| 冲次/min-1 | 2.3 |
| 沉没度/m | 150 |
| 泵间隙等级 | 3 |
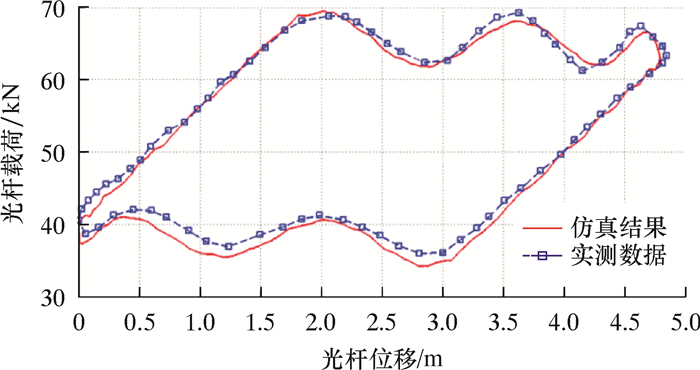
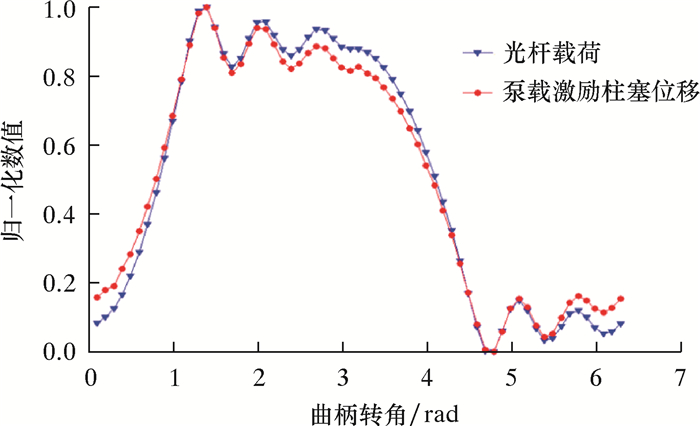
仿真计算结果如图 2和图 3所示。从图 2可以看出,悬点载荷的仿真值与现场数据之间具有良好的一致性,验证了运动分解方法的正确性。由图 3可知,由子运动2得到的柱塞运动规律与悬点载荷振动规律有很好的符合性,这说明分离出的柱塞振动位移可以反映悬点载荷的变化规律。
|
| 图 2 实测示功图与仿真结果对比 Fig.2 Comparison of measured dynamometer diagram and simulation results |
|
| 图 3 光杆载荷和时变载荷引起的柱塞位移归一化对比 Fig.3 Normalized comparison of plunger displacement caused by polished rod load and time-varying load |
4 柱塞超冲程问题分析 4.1 柱塞位移分解
由分解模型得到的结果计算柱塞位移,如式(16)~式(18)所示。
悬点位移激励引起的柱塞位移为:
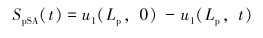
|
(16) |
泵时变载荷引起的柱塞位移为:
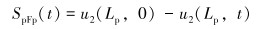
|
(17) |
柱塞瞬时位移为:
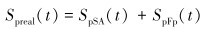
|
(18) |
假设油管锚定,静力冲程损失为:
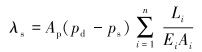
|
(19) |
式中:Ap为柱塞截面面积,Li、Ei、Ai分别为第i级杆柱的长度、弹性模量和截面面积,n为抽油杆的级数。
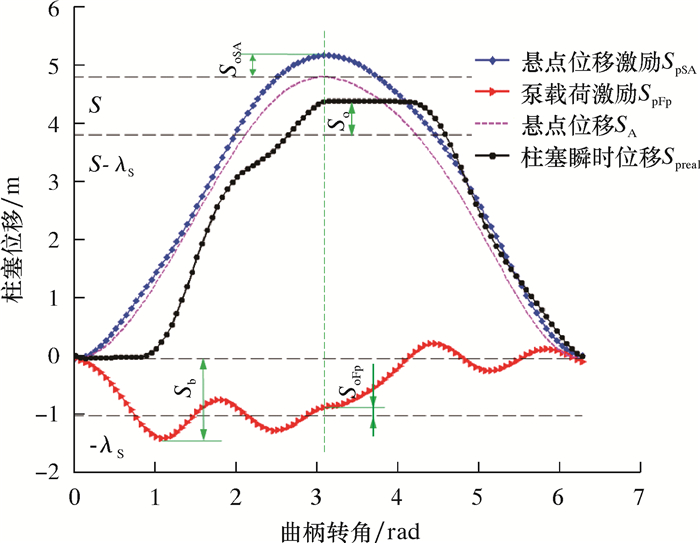
冲次为5 min-1时,以表 1为基本参数,模型仿真结果如图 4所示。从图 4可以看出,由悬点位移激励产生的柱塞最大位移大于悬点的最大位移,记差值为共振超冲程SoSA;由泵时变载荷引起的柱塞位移在柱塞上行截止时并不与静力冲程损失λs相等,记其差值为谐振超冲程SoFp;共振超冲程与谐振超冲程共同组成了柱塞的相对超冲程(柱塞实际冲程与静力冲程S-λs的差值)So;由泵时变载荷引起的柱塞位移的最大绝对值记为Sb,可反映悬点的最大载荷值。
|
| 图 4 柱塞位移分解 Fig.4 Plunger displacement decomposition |
柱塞的有效冲程为:
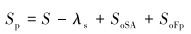
|
(20) |
式中:S为悬点最大位移,m。
从上述分析可以得出,悬点位移的激励和泵时变载荷激励共同影响着柱塞的超冲程。
4.2 冲次对柱塞超冲程的影响以典型井参数为例,分析冲次对柱塞冲程的影响。典型井基本参数如表 2所示。仿真结果如图 5和图 6所示。
| 参数名称 | 数值 |
| 泵径/mm | 38 |
| 泵挂/m | 2 000 |
| 碳杆直径/mm | 16 |
| 碳杆密度/(kg·m-3) | 1 960 |
| 碳杆弹性模量/GPa | 95 |
| 钢杆直径/mm | 25 |
| 钢杆密度/(kg·m-3) | 7 950 |
| 钢杆弹性模量/GPa | 211 |
| 碳杆占比 | 0.67 |
| 油管内径/mm | 62 |
| 井液密度/(kg·m-3) | 900 |
| 含水体积分数/% | 80 |
| 油压/MPa | 0.2 |
| 套压/MPa | 0.3 |
| 生产油气比/(m3·m-3) | 0 |
| 井液动力黏度/(mPa·s) | 20 |
| 冲程/m | 4.8 |
| 冲次/min-1 | 1~7 |
| 沉没度/m | 150 |
| 泵间隙等级 | 3 |
|
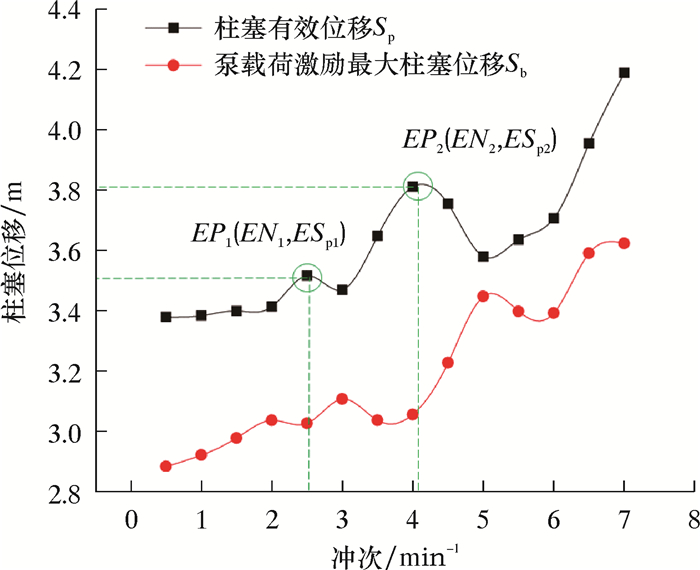
| 图 5 冲次对柱塞位移的影响 Fig.5 Effect of the stroke on the displacement of the plunger |
|
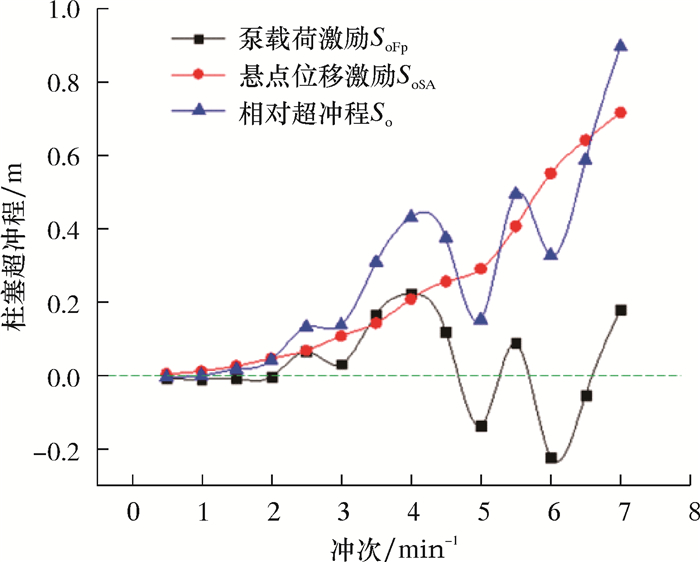
| 图 6 冲次对柱塞超冲程的影响 Fig.6 Effect of the stroke on the plunger over stroke |
从图 5可以看出,随着冲次的增加,柱塞的有效位移Sp随着冲次的增加并不是单调上升的,而是波动上升的,存在极大值点(EP1,EP2),且极大值点的个数不唯一。定义极大值点处的冲程为极值冲程ESp,冲次为极值冲次EN。泵时变载荷引起的柱塞最大位移Sb并不处于极大值处,反而处于极小值附近,表明在柱塞有效位移取得极大值时,并不会伴随极大的悬点载荷。
从图 6可以看出,悬点激励引起的超冲程随着冲次的增加而单调增加,原因是抽油装备的许用冲次小于杆柱振动的固有频率,随着冲次的增加,越靠近杆柱的固有频率,振幅也随之增加。而泵时变载荷引起的超冲程有正有负,即泵载荷的时变性既可能增加柱塞的有效冲程,也可能减小柱塞的有效冲程。这与上冲程柱塞振动结束时的振动截止相位Φ有关。当截止相位处于前半周期,即2kπ < Φ < (2k+1)π,此情况下,泵时变载荷引起的超冲程为负,此时泵载荷的时变性降低柱塞的有效冲程。当截止相位处于后半周期,即(2k+1)π < Φ < (2k+2)π,此情况下,泵时变载荷引起的超冲程为正,此时泵载荷的时变性增加柱塞的有效冲程,这也是产生极值冲程的原因。
从图 6还可以看出,极值冲程并不是微小量,以该典型井为例,在第二极大值点处,柱塞的相对超冲程为0.48 m,可使抽油泵的容积效率提高10%。极值冲次小于地面抽油设备的许用冲次,可用于工程实际。
4.3 杆柱组合对柱塞超冲程的影响全钢杆杆柱和混合杆柱的组合参数如表 3所示。其中全钢杆杆柱规格为ø19 mm×2 000 m,混合杆柱规格为ø22 mm×1 000 m碳杆+ø25 mm×1 000 m钢杆。柱塞有效冲程与冲次之间的仿真结果如图 7所示。
| 名称 | 泵径/mm | 冲程/m | 泵挂/m | 沉没度/m | 杆柱浮重/kN |
| 全钢杆 | 56 | 4.8 | 2 000 | 200 | 43.7 |
| 混合杆柱 | 56 | 4.8 | 2 000 | 200 | 36.6 |
|
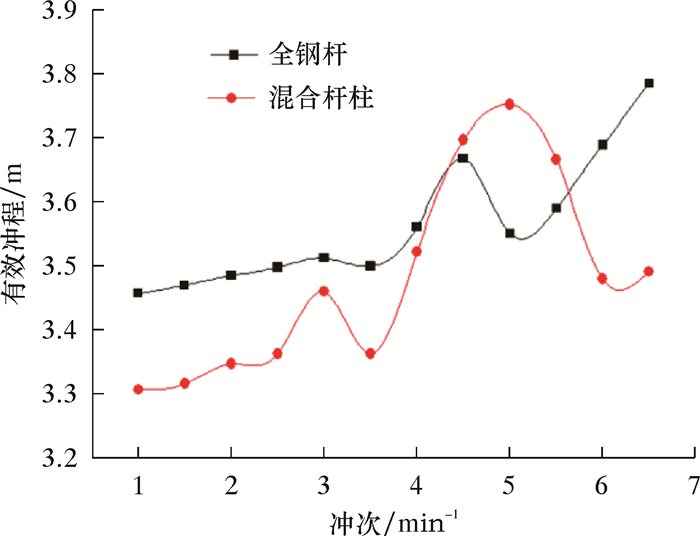
| 图 7 全钢杆与混合杆柱塞柱有效冲程 Fig.7 Effective plunger stroke of all steel rod and mixed rod string |
从图 7可看出,在冲次较低时,全钢杆的柱塞有效冲程大于混合杆柱,因为全钢杆的静力冲程损失较小。全钢杆也存在极值冲程,但在许用冲次以内,相对值较小,即泵载荷时变性对柱塞有小冲程的影响较小。在许用冲次以内,全钢杆的最大柱塞有效冲程在冲次为6 min-1时取得,为3.69 m,相对超冲程为0.23 m;混合杆柱的最大柱塞有效冲程在冲次为5 min-1取得,为3.75 m,相对超冲程为0.45 m。这表明在许用冲次内,混合杆柱取得最大柱塞有效冲程时的冲次小于全钢杆,且混合杆柱最大柱塞有效冲程的绝对值和相对超冲程均大于全钢杆。同时,由表 3可以看出混合杆柱的质量较轻,可以减小悬点载荷。当选取合适生产参数时,使用混合杆柱不仅可以提高泵效,还可以降低能量损耗。
5 结论(1) 将抽油杆柱的运动分解为由悬点位移激励和泵时变载荷激励引起的杆柱振动,建立了分解运动数学模型,经现场试验,验证了模型的准确性。
(2) 分析了冲次对柱塞超冲程的影响,结果表明悬点位移激励产生的柱塞超冲程随着冲次的增加而单调增加,泵时变载荷引起的超冲程有正有负,与上冲程柱塞振动结束时的振动截止相位有关。
(3) 提出了极值冲程和极值冲次的概念,并指出泵载荷的时变性产生了极值冲程。极值冲程不是微小量,可将泵容积效率提高10%。极值冲次小于地面采油设备的许用冲次,可用于工程实际。
(4) 分析了杆柱组合对柱塞超冲程的影响,结果表明在合适的生产参数下,混合杆柱塞有效冲程的绝对值和相对超冲程均大于全钢杆。同时,由于混合杆柱的自身质量较轻,可降低能量损耗。无论从能耗还是从泵效角度,碳纤维-钢混合杆柱均优于全钢杆。研究结果为现场合理设计使用碳纤维抽油杆提供了理论依据。
| [1] |
FOLEY W L, HENSLEY H N. Ribbon rod: improvement in sucker rod technology shows need to re-evaluate current artificial lift installation[R].SPE 35708, 1996.
|
| [2] |
吴则中, 田丰, 张海宴, 等. 碳纤维复合材料连续抽油杆的特点及应用前景[J]. 石油机械, 2002, 30(2): 53-56. WU Z Z, TIAN F, ZHANG H Y, et al. Characteristics and application prospect of carbon fiber composite continuous sucker rod[J]. China Petroleum Machinery, 2002, 30(2): 53-56. DOI:10.3969/j.issn.1001-4578.2002.02.018 |
| [3] |
朱波, 蔡华苏, 孙乃武. 碳纤维复合材料柔性连续抽油杆开发及应用[J]. 石油机械, 2003, 31(1): 29-31. ZHU B, CAI H S, SUN N W, et al. Development and application of carbon fiber reinforced plastic continuous sucker rod[J]. China Petroleum Machinery, 2003, 31(1): 29-31. DOI:10.3969/j.issn.1001-4578.2003.01.010 |
| [4] |
王志刚, 乜冠祯, 高军, 等. 碳纤维连续抽油杆在纯梁油田的应用[J]. 石油钻探技术, 2005, 33(4): 58-59. WANG Z G, NIE G Z, GAO J, et al. Applications of carbon fiber coiled rod in the Chunliang block[J]. Petroleum Drilling Techniques, 2005, 33(4): 58-59. DOI:10.3969/j.issn.1001-0890.2005.04.020 |
| [5] |
GIBBS S G. Predicting the behavior of sucker-rod pumping systems[J]. Journal of Petroleum Technology, 1963, 15(7): 769-778. DOI:10.2118/588-PA |
| [6] |
DOTY D R, SCHMIDT Z. Improved model for sucker rod pumping[J]. Soc. Pet. Eng. AIME, 1983, 23(1): 33-41. DOI:10.2118/10249-PA |
| [7] |
余国安, 邬亦炯, 王国源. 有杆泵抽油井的三维振动[J]. 石油学报, 1989, 10(2): 76-83. YU G A, WU Y J, WANG G Y. Three dimensional vibration in a sucker rod beam pumping system[J]. Acta Petrolei Sinica, 1989, 10(2): 76-83. DOI:10.3321/j.issn:0253-2697.1989.02.002 |
| [8] |
刘芳超, 王素玲, 徐广元, 等. 细长抽油杆柱振动特性数值研究[J]. 钻采工艺, 2013, 36(6): 82-85. LIU F C, WANG S L, XU G G, et al. Numerical simulation study on vibration performance of slender rod[J]. Drilling & Peoduction Technology, 2013, 36(6): 82-85. DOI:10.3969/J.ISSN.1006-768X.2013.06.24 |
| [9] |
LUAN G H, HE S L, YANG Z, et al. A prediction model for a new deep-rod pumping system[J]. Journal of Petroleum Science and Engineering, 2011, 80(1): 75-80. DOI:10.1016/j.petrol.2011.10.011 |
| [10] |
XING M. Response analysis of longitudinal vibration of sucker rod string considering rod buckling[J]. Advances in Engineering Software, 2016, 99: 49-58. DOI:10.1016/j.advengsoft.2016.05.004 |


