2. 中国石化石油工程技术研究院;
3. 中国石油大学(北京)油气资源与探测国家重点实验室;
4. 西安石油大学石油工程学院
2. Sinopec Research Institute of Petroleum Engineering;
3. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum(Beijing);
4. College of Petroleum Engineering, Xi'an Shiyou University
0 引言
非常规储层由于其低孔低渗特性,需要进行压裂才能形成具有开采价值的工业油气流[1-3]。然而,由于我国非常规油气主要富集于缺水地区,且储层内黏土含量普遍较高,常规水力压裂供水资源耗费大,所用压裂液易污染地下水,而返排液易导致地表水和土壤污染;黏土矿物水敏性强,而水敏性强的储层遇水易发生水化膨胀,压裂液残渣易堵塞渗流通道而对储层造成不可逆的伤害[4]。这些使得水力压裂在非常规储层改造中的应用受到极大限制,法国、西班牙和德国等已经明确立法禁止使用水力压裂法开采油气。CO2具有超强的吸附能力,可以置换出非常规储层内的甲烷而提高储层采收率;同时CO2兼具埋存和减缓温室效应的作用[5];CO2流体作为压裂液能够明显降低地层起裂压力,相对于常规压裂液其降低幅度超过50%,且CO2流体压裂存在多次起裂过程,更有利于复杂裂缝的形成[4, 6]。CO2的这些特点使得CO2干法压裂成为非常规储层改造的一种有效手段。
CO2干法压裂过程中,井筒压力、温度和相态的准确控制是影响裂缝起裂和延伸的关键因素,并且能够指导压裂泵车及油管选择。目前CO2干法压裂过程中井筒压力和相态控制方面缺乏研究,仅部分学者开展了关于超临界CO2压裂井筒流动传热研究(由于携砂和密封性问题,文献内未见其现场应用情况),研究重点集中在超临界态实现与控制,工艺参数对井筒流动传热影响因素分析[5, 7-8]。鉴于此,笔者在考虑压裂大排量下流体摩擦生热的情况下,采用高精度的CO2物性状态方程,建立了CO2干法压裂过程中井筒流动模型,以现场压裂施工参数为依据,分析了CO2干法压裂过程中井筒压力控制机理,并优化了对应的施工工艺参数。研究结果可为CO2干法压裂和CO2增能压裂提供理论指导和现场借鉴。
1 井筒流动与传热数学模型 1.1 基本假设压裂过程中CO2流体物性与井筒传热、流动相互耦合,且在井筒范围内CO2流体可能存在相态转变。考虑其复杂性,对模型做部分简化[9-10]:①假定其为一维流动,同一截面上流体温度压力以及CO2流体物性相同;②地层到井壁处为非稳态传热,井壁至油管内为稳态传热;③由大排量产生的摩擦热量只与摩擦压降梯度和流速相关,并且作为内热源处理;④忽略由于CO2相变引起的能量变化。
1.2 井筒流动压降模型CO2相对于常规水基压裂液具有较高的压缩性,其密度随温度和压力动态变化导致流速非恒定,其连续性方程为:
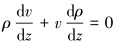
|
(1) |
式中:ρ为CO2密度,kg/m3;z为井筒所划分单元格长度,m;v为CO2流速,m/s。
结合连续性方程和动量定理,CO2干法压裂过程中油管内向下流动压降公式为:
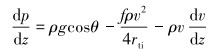
|
(2) |
式中:p为CO2流体压力,kPa;g为重力加速度,取值9.81 m/s2;θ为井斜角,(°);rti为油管内半径,m;f为油管内达西摩擦因数。
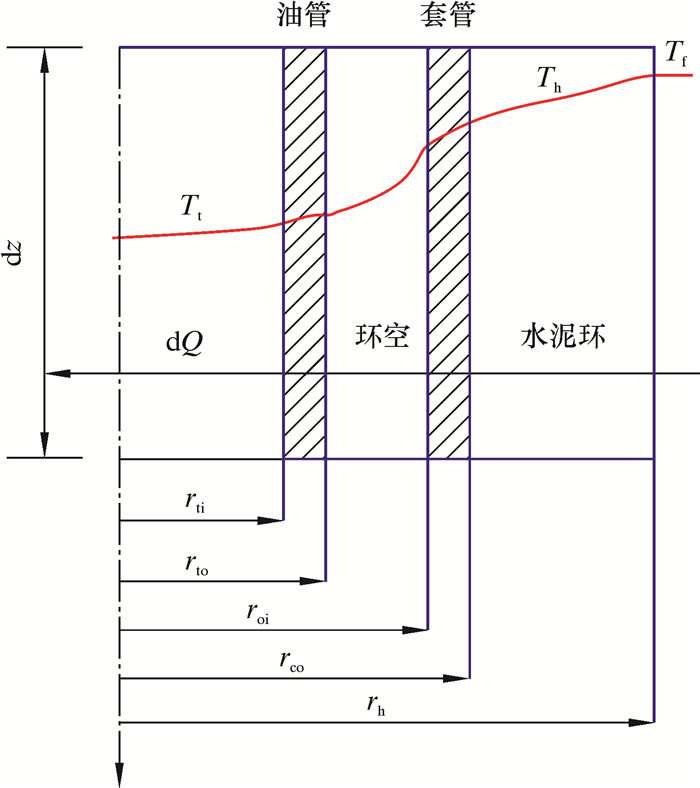
1.3 井筒传热模型假定正方向向下,沿井筒方向取dz微元(见图 1),考虑摩擦生热做功,根据C.S.KABIR和A.R.HASAN[11]提出的井筒传热模型建立其能量守恒方程。
|
| 图 1 CO2压裂井筒流动及传热模型 Fig.1 Wellbore flow and heat transfer model of CO2 fracturing |
油管内CO2流体温度计算表达式为:
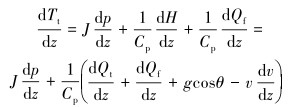
|
(3) |
式中:Tt为微元段流体温度,℃;J为焦耳-汤姆逊系数,℃/MPa;Cp为CO2流体的定压比热容,J/(kg·℃);H为CO2流体比焓,kJ/kg;Qt为井筒环空到油管内传热量,kJ;Qf为流体流动摩擦做功产生的热量,kJ。
其中:
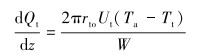
|
(4) |
式中:W为CO2流体质量流量,kg/s;rto为油管外半径,m;Ut为油管内流体与环空中流体之间的综合传热系数,W/(m2·℃);Ta为环空流体温度,℃。
联立式(3)和式(4),并考虑摩擦压降生热,可得到:
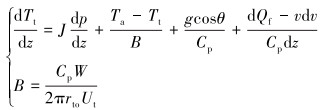
|
(5) |
式(5)中的环空流体温度Ta可通过式(6)~式(10)计算得到,摩擦生热Qf变量则可通过式(11)计算得到。
地层与水泥环外缘传热是非稳态的,其传热量dQ计算方程为:
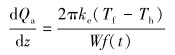
|
(6) |
式中:Tf为地层温度,℃;ke为地层导热系数,W/(m·℃);f(t)为瞬态传热函数,其详细计算公式可参考文献[12];Th为水泥环外缘温度,℃。
水泥环外缘与环空间传热量dQ计算方程为:
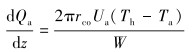
|
(7) |
式中:Ua为环空内流体与地层之间的综合传热系数,W/(m2·℃);rco为套管外半径,m。
环空内流体温度计算表达式为:
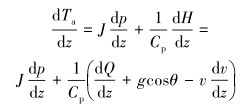
|
(8) |
环空中流体在径向上传入钻柱内流体的热量为dQp/dz,在径向上由井壁传入环空内流体的热量为dQa/dz,因此有:
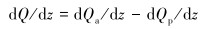
|
(9) |
联立式(6)~式(9),消去Th,可得环空流体能量守恒方程:
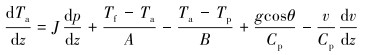
|
(10) |
其中: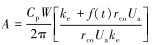
CO2流体压裂过程中排量非常大,此时摩擦力做功产生的内热源不可忽略,其计算公式为:
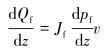
|
(11) |
式中:Jf为摩擦力做功能量转化系数,℃/(MPa·s)。
2 相关参数计算及模型求解 2.1 CO2流体密度和定压热容CO2状态方程选用Span-Wagner模型[13],其采用Helmholtz自由能计算CO2流体物性,在井筒温度范围内密度误差控制在0.05%以内,其他条件下误差控制在3.0%以内。Helmholtz自由能方法以流体密度和温度为自变量,其通用计算式为:
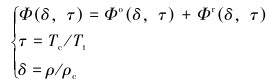
|
(12) |
式中:Φ为Helmholtz自由能;Φo为Helmholtz自由能理想部分;Φr为Helmholtz自由能残余部分;τ为对比温度倒数;δ为对比密度;Tc为临界温度,K;ρc为临界密度,kg/m3。
CO2流体密度的隐性计算式为:
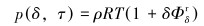
|
(13) |
式中:R表示普适气体常数,取值为8.314 5 J/(mol·℃);Φδr为Φr对δ的一次偏导。
同样,CO2流体密度定压热容表达式为:
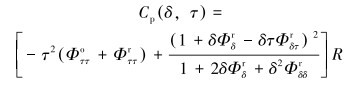
|
(14) |
式中:Φττo、Φττr、Φδτr、Φδδr是Φo或ør对δ和τ的二次偏导。
2.2 黏度和导热系数CO2流体黏度和导热系数分别采用A.FENGHOUR和V.VESOVIC等[14-15]的计算方法,常压条件下其计算误差控制在0.3%以内,高压条件下其误差控制在5%以内,能满足工程计算要求。
在油管内CO2流体与油管壁换热属于强对流,换热系数计算可采用如下公式[8]:
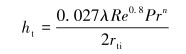
|
(15) |
式中:ht为油管内CO2流动时对流换热系数,W/(m2·℃);Re、Pr分别为雷诺数和普朗特数,无因次;n为指数系数,流体被冷却状态时取值0.3,被加热状态时取值0.4。
2.3 摩擦因数计算CO2流体干法压裂过程中摩阻非常大,因而摩擦因数选择时既要考虑雷诺数对其影响,也要考虑表面粗糙度的影响,故选用N.H.CHEN[16]提出的摩擦因数表达式。
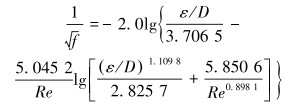
|
(16) |
式中:ε为油管内径平均表面粗糙度,m;D为油管内径,m。
2.4 模型求解从流动和传热模型可知,CO2流体压裂时油管内压力和流速变化影响CO2温度,而温度变化影响流体密度变化,进而影响流体体积和流速变化,导致井筒压力变化,因此井筒温度、压力和CO2物性相互影响,需要耦合计算求解。具体求解流程如下:①将整个井筒均等划分为N个微元段,在各个节点上进行数学离散;②采用牛顿迭代计算CO2流体压力;③采用四阶龙格-库塔方法计算温度;④通过迭代求解温度、压力和CO2流体物性参数,直到达到规定的收敛条件为止。
3 算例分析 3.1 实例参数由于缺乏CO2干法压裂过程中井筒和井底温度压力实测数据,所以参考现场实际施工作业情况。以鄂尔多斯盆地X井长7页岩储层CO2增能压裂地层、井筒和工艺参数为例进行计算与分析,具体数据见表 1。利用所建模型和X井现场数据开展井筒流动、温度、相态以及携砂能力分析。
| 参数名称 | 数值 |
| 井深/m | 2 650 |
| 油管外径/mm | 73.0 |
| 油管壁厚/mm | 5.51 |
| 油层套管外径/mm | 139.7 |
| 套管壁厚/mm | 7.72 |
| 井筒直径/mm | 215.9 |
| 注入压力/MPa | 30 |
| 注入温度/℃ | -20 |
| 地表温度/℃ | 20 |
| 地温梯度/(℃·m-1) | 0.035 |
| 注入排量/(m3·min-1) | 2.5 |
| 注入时间/min | 60 |
| 地层比热容/(J·kg-1·℃-1) | 837 |
| 地层导热系数/(W·m-1·℃-1) | 2.25 |
| 水泥石比热容/(J·kg-1·℃-1) | 2 000 |
| 水泥石导热系数/(W·m-1·℃-1) | 0.7 |
3.2 井筒CO2流体温度和压力影响因素分析 3.2.1 施工排量影响
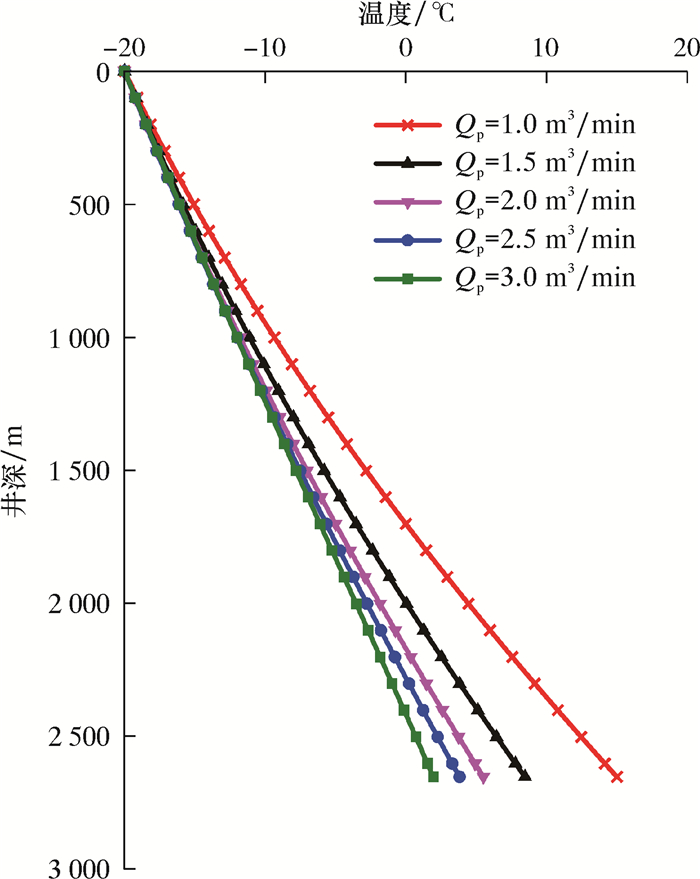
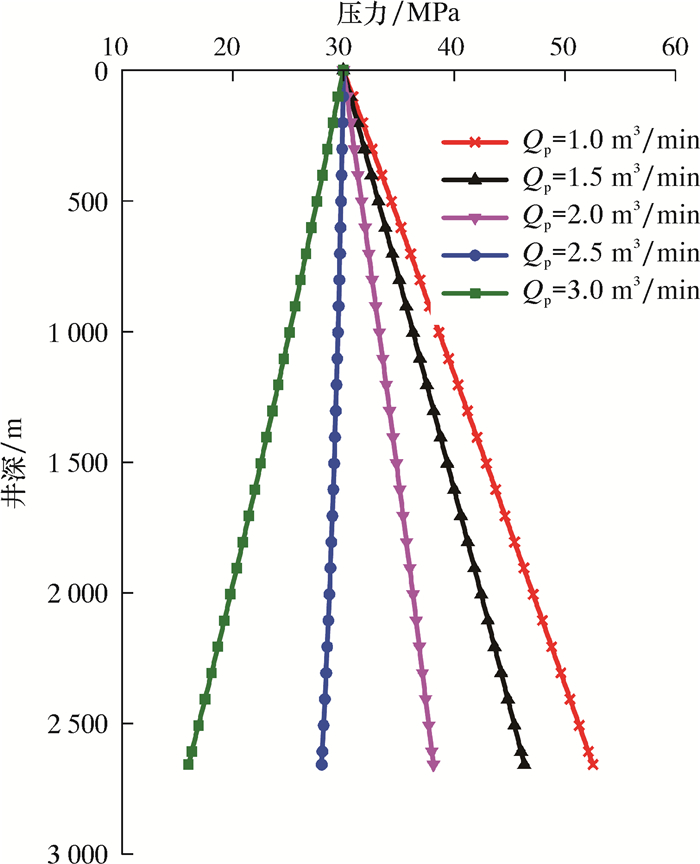
图 2和图 3分别为注入压力一定时CO2注入排量Qp由1.0 m3/min增至3.0 m3/min时井筒CO2流体温度和压力的变化规律。
|
| 图 2 不同施工排量下井筒温度剖面 Fig.2 Wellbore temperature profile under different displacements |
|
| 图 3 不同施工排量下井筒压力剖面 Fig.3 Wellbore pressure profile under different displacements |
从图 2可知:井筒内CO2流体温度随井深增加而升高,施工排量增大,井筒温度降低;随井深增加其影响程度增大。其原因是施工排量越大,在油管内CO2流体速度越大,与地层热交换时间变短,热交换量减少,导致其温度降低;整体而言,施工排量达到2.0 m3/min以上时对井底温度影响明显减小。
从图 3可知,相同井深时,随施工排量增大,井筒压力明显减小。采用常规油管(ø73.0 mm)压裂时,因施工排量较大,井筒内CO2流体摩阻非常大(排量为2.0 m3/min时,CO2流体沿程摩阻每1 000 m超过10 MPa,而同样排量下采用胍胶压裂液其沿程摩阻每1 000 m仅为4~5 MPa),使得井底压力明显降低。压裂过程中若要保持井底压力稳定,裂缝顺利延伸,则需要保持非常高的井口注入压力,这对CO2干法压裂地面设备泵注能力提出了更高要求,因而有必要研发相应的CO2流体减阻剂,降低大排量施工时沿程摩阻,提高压裂效率。
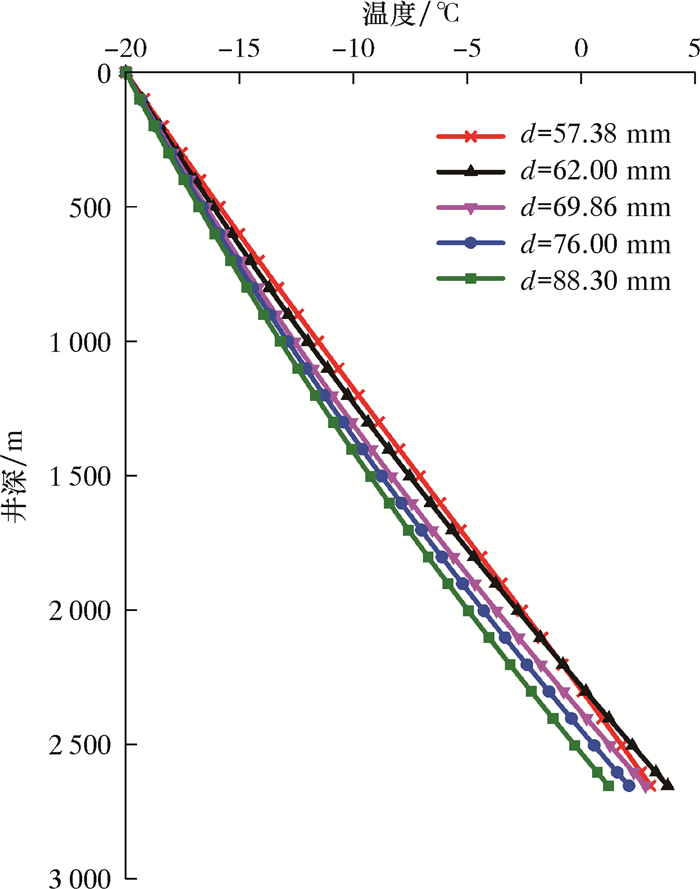
3.2.2 施工油管内径影响分析了常用的5种油管内径d(57.38、62.00、69.86、76.00和88.30 mm)对井筒温度和压力的影响。图 4为不同油管内径条件下井筒温度剖面。
|
| 图 4 不同油管内径下井筒温度剖面 Fig.4 Wellbore temperature profile under different tubing inner diameters |
从图 4可知,当施工排量一定时(2.5 m3/min),随油管内径增大,井筒内CO2流体温度逐渐降低,在上部井段影响较小,随井深增加其影响程度增大。其原因是:从图 2可知,在相同排量下油管内径增大其流速降低,热交换时间延长导致CO2流体温度略升高,但油管内径越大其单位体积流体的热交换量降低。总体而言,流体温度降低量高于其热交换时间增加的温度增量,因而随着油管内径增大,其内流体温度呈下降趋势。
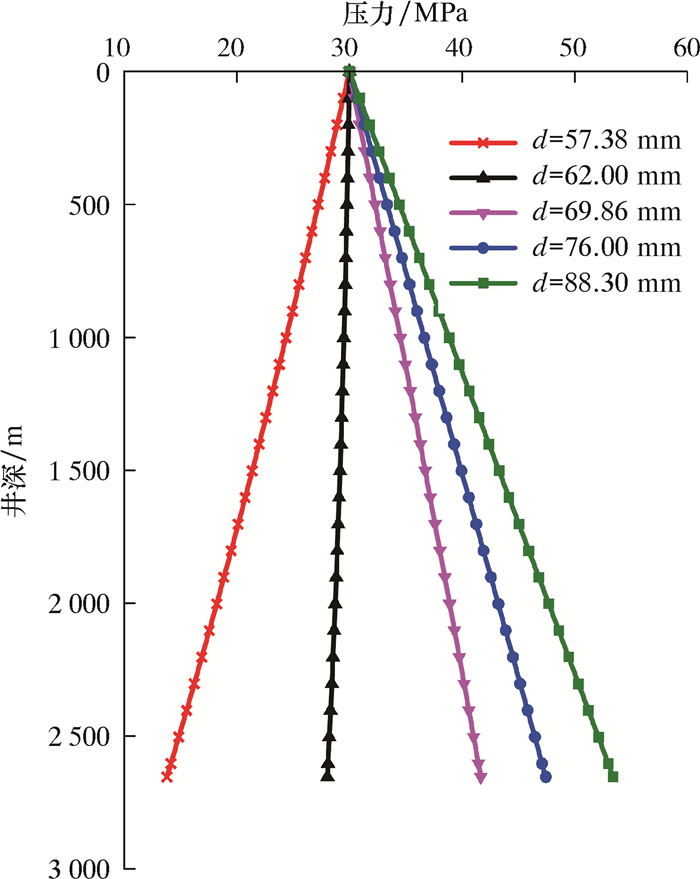
图 5为不同油管内径条件下井筒压力剖面。从图 5可知,当施工排量一定时(2.5 m3/min),随油管内径增大,井筒内CO2流体压力明显增大。其主要原因是:当排量一定时,油管内径越大,井筒内CO2流体流动过程中需要克服的摩擦阻力越小,导致井底压力明显增大。
|
| 图 5 不同油管内径下井筒压力剖面 Fig.5 Wellbore pressure profile under different tubing inner diameters |
3.2.3 注入温度影响
图 6为井筒内温度随CO2流体井口注入温度变化曲线。从图 6可知,随井口CO2流体注入温度升高,井筒内流体温度明显升高。当井口注入温度为-10 ℃时,井底温度可达13 ℃,CO2仍处于液态,井口注入温度对井底流体温度影响极大,近乎线性提高。采用CO2干法压裂时应合理控制井口注入温度,避免井筒CO2流体温度高于临界温度而发生相态转变。相态转变对于井筒压力控制和携砂都有较大影响。

|
| 图 6 不同注入温度下井筒温度剖面 Fig.6 Wellbore temperature profile at different injection temperatures |
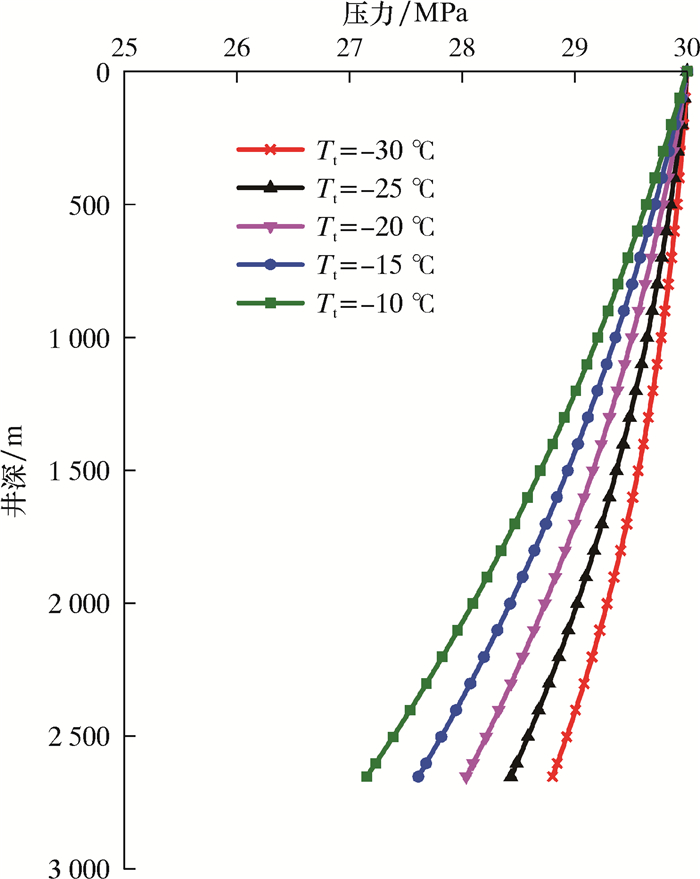
图 7为井筒压力随CO2流体井口注入温度变化曲线。从图 7可知,随注入温度升高,井筒压力减小,这主要是因为流体温度升高,其密度减小了。
|
| 图 7 不同注入温度下井筒压力剖面 Fig.7 Wellbore pressure profile at different injection temperatures |
3.3 CO2流体携砂能力分析 3.3.1 施工排量影响
图 8为不同施工排量下油管内CO2流体密度剖面。从图 8可知,当井口压力一定时,随排量增大CO2流体密度减小,CO2流体密度对温度和压力都比较敏感。不同施工排量下,从图 2可知其井筒温度变化不是很明显,但从图 3可知井筒压力变化非常大,导致CO2流体密度在不同排量下受井筒压力影响更大,其密度剖面与井筒压力剖面呈正相关。流体密度小不利于携砂,这部分抵消了由于排量增大所带来的携砂能力提高的效果。

|
| 图 8 不同注入排量下井筒密度剖面 Fig.8 Wellbore density profile under different injection displacements |
图 9为不同施工排量下油管内CO2流体黏度剖面。

|
| 图 9 不同注入排量下井筒黏度剖面 Fig.9 Wellbore viscosity profile under different injection displacements |
从图 9可知,当井口压力一定时,随施工排量增大,油管内CO2流体黏度减小。CO2流体黏度变化趋势与密度变化趋势类似,但是相对密度,黏度变化范围更大,排量对黏度的影响也更加显著。流体黏度的降低部分抵消了由于排量增加所带来的携砂能力的提高。
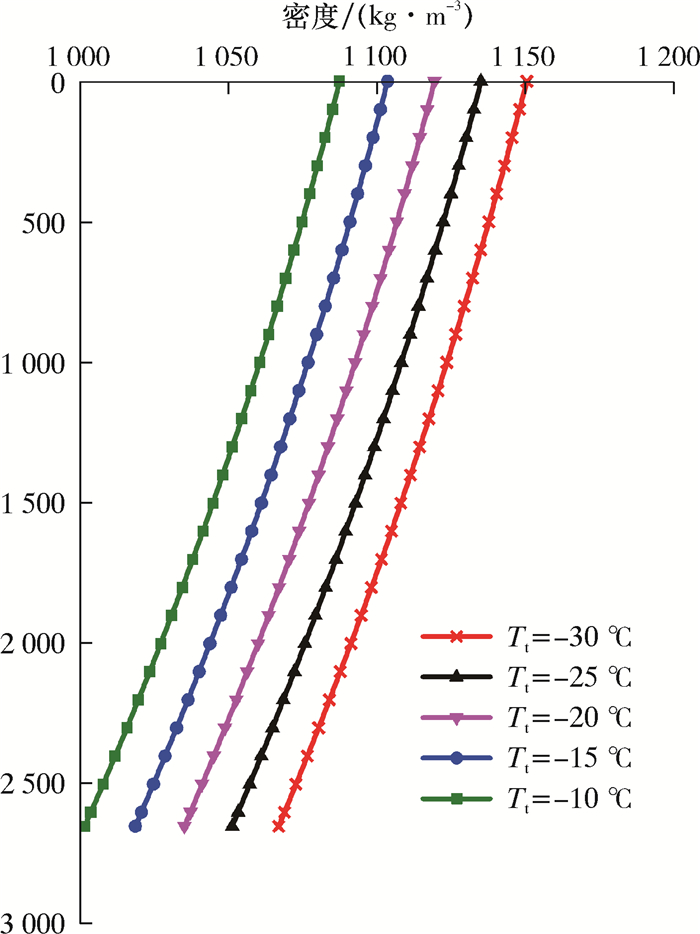
3.3.2 注入温度影响图 10为不同注入温度下油管内CO2流体密度剖面。从图 10可知,CO2流体密度随注入温度升高而减小。从图 6和图 7可知,井筒流体温度受注入温度影响明显,而压力受其影响较小。由于CO2流体密度对温度非常敏感,所以高注入温度会升高井筒温度,进而导致流体密度偏低。CO2干法压裂现场施工作业中应尽量保持较低的注入温度,这样既能避免井筒内流体发生相态转变,又能维持较高的CO2流体密度,提高流体携砂能力。
|
| 图 10 不同注入温度下井筒密度剖面 Fig.10 Wellbore density profile at different injection temperatures |
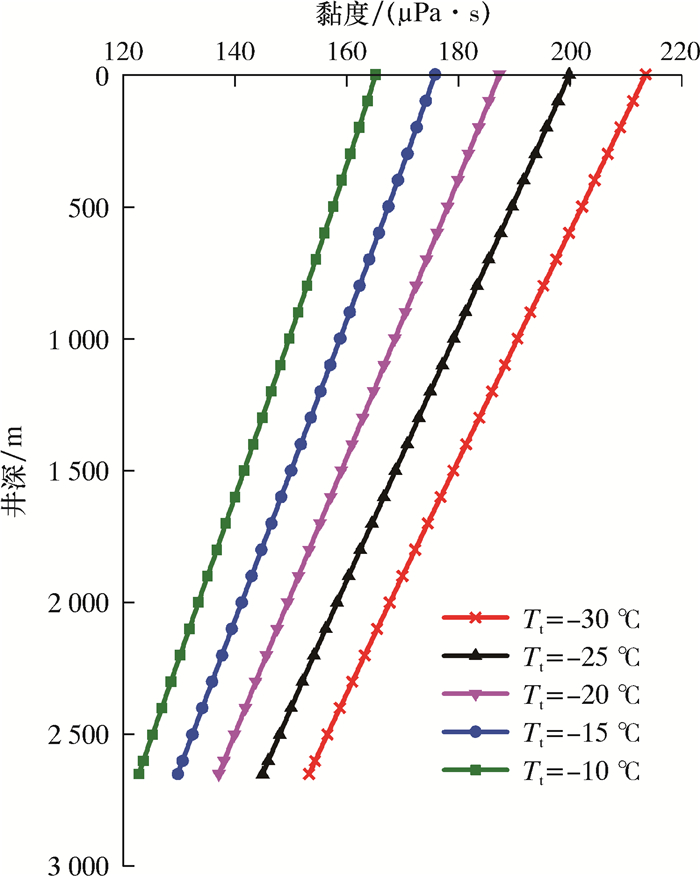
图 11为不同注入温度下油管内CO2流体黏度剖面。从图 11可知,不同注入温度条件下CO2流体黏度变化趋势与密度变化趋势类似,但是黏度相对密度受影响程度更大,其变化范围更大,且在井口处由于注入温差较大导致流体黏度差异大,随着井深增加,CO2流体黏度差异减小。注入温度越高,流体黏度越小,因此在施工时应尽量采用较低的注入温度,提高CO2流体携砂能力。
|
| 图 11 不同注入温度下井筒黏度剖面 Fig.11 Wellbore viscosity profile at different injection temperatures |
在常规CO2干法压裂施工条件下,CO2流体黏度仅为0.08~0.25 mPa·s,携砂能力差,加之进入储层后易转变为超临界态,界面张力变为零,滤失量极大,不利于裂缝扩展,易导致压裂施工失败。施工过程中可通过在限压范围内提高施工排量,加入增稠剂或增黏剂提高CO2流体黏度,以及采用超低密度支撑剂等措施来提高CO2流体携砂能力,进而提高压裂效果。
3.4 相态分析CO2临界温度是31.06 ℃,临界压力是7.38 MPa(只有当压力和温度同时超过其临界值,CO2才由液态转变为超临界态)。从图 3、图 5和图 7可知,不同施工工艺参数条件下,井筒内压力一般高于其临界压力,如果温度低于临界温度则为液态,高于其临界温度则为超临界态。因而CO2流体在井筒内是否会发生由液态(CO2流体压裂时注入流体为液态)向超临界态转变取决于流体温度是否达到其临界温度。井筒内最高温度未超过临界温度,CO2流体在全井筒范围内保持为液态,避免了由于相态变化导致的压力波动;如果采用超临界CO2压裂,则需要井底温度超过其临界温度,一般需要通过提高注入温度来实现。另外,不同地区地温梯度差异较大,同样对CO2相态转变有一定影响。因此,笔者主要以CO2流体注入温度和地温梯度分析其井筒流动过程中可能出现的相态转变。
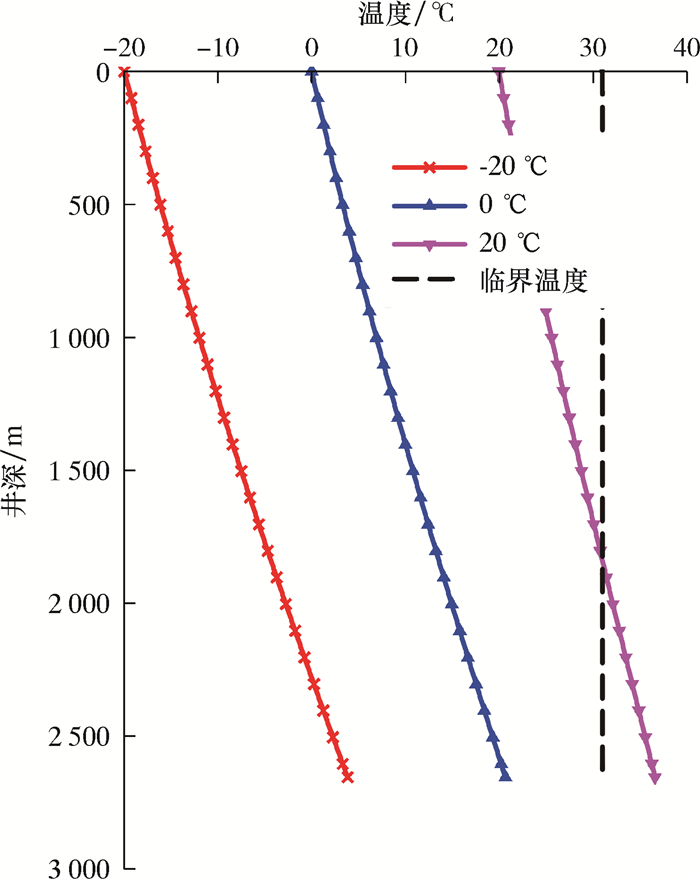
图 12为不同井口注入温度条件下井筒流体温度分布和相态图。采用CO2干法压裂时井口注入温度一般在-20 ℃,在2 650 m井底处出现最高流体温度为3.84 ℃(见图 12),即便采用1.0 m3/min排量,其井底温度也为15.05 ℃(见图 2),明显低于CO2流体临界温度31.06 ℃,因而CO2干法压裂时,采用常规的注入温度和施工排量,CO2流体在井筒范围内不会发生相态转变。但井筒注入温度较高时(如图 12中注入温度为20 ℃),可能在井底附近发生相态转变,CO2流体由液态转变为超临界态,因而CO2干法压裂和超临界CO2压裂其井口注入温度有明显差别,一般超临界CO2压裂其井口注入温度相对较高,便于CO2流体在井底附近转变为超临界态,而CO2干法压裂则要求应保持较低的注入温度,以避免出现相态转变。
|
| 图 12 不同注入温度时井筒流体温度分布及相态 Fig.12 Temperature distribution and phase state of wellbore fluid at different injection temperatures |
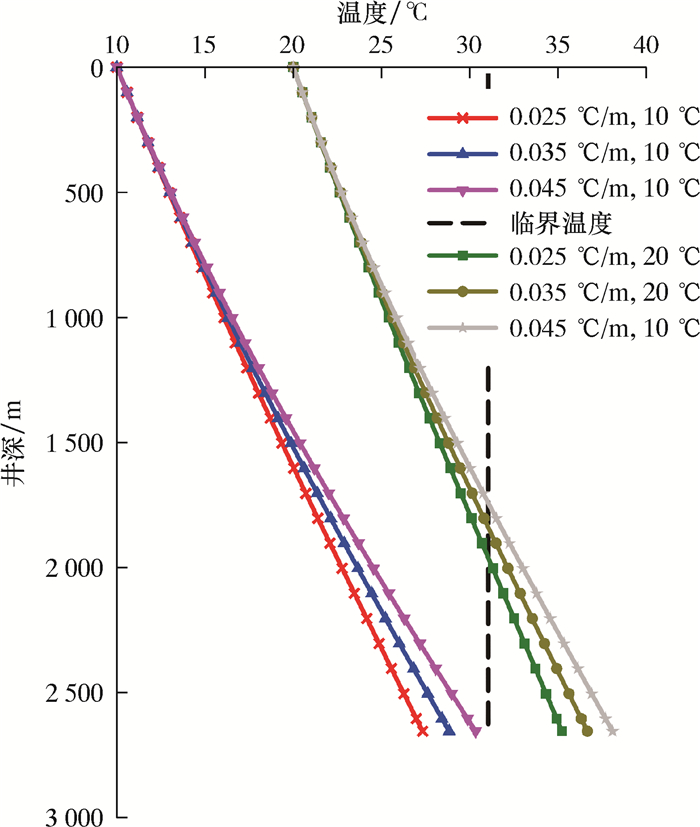
图 13为不同地温梯度时井筒流体温度分布及相态图。
|
| 图 13 不同地温梯度下井筒流体温度分布及相态 Fig.13 Temperature distribution and phase state of wellbore fluid under different geothermal gradients |
从图 13可知:当井口注入温度为10 ℃、不同地温梯度时,其井底温度均未超过临界温度;而当注入温度为20 ℃、不同地温梯度时,其井底温度均超过临界温度;井口流体注入温度的影响远大于地温梯度的影响。因而在地温较高井或较深井应用CO2干法压裂时,可通过适当控制井口注入温度,避免发生相态转变而导致的井筒压力控制不稳定以及影响其携砂能力。
4 结论及建议(1) CO2流体摩阻非常高,在ø73.0 mm油管(内径62.00 mm)排量为2 m3/min时,其沿程摩阻每1 000 m已超过10 MPa,因而有必要研发CO2流体专用减阻剂,以减小大排量施工时的流体摩阻,提高压裂效率,降低作业成本。
(2) CO2注入排量和油管内径对井底压力影响非常大,在大排量和(或)小尺寸油管注入时井筒压力甚至出现随井深增加而降低的现象,不利于裂缝起裂和延伸,因而可通过适当降低排量或选用较大管径油管实施CO2干法压裂以降低摩阻,提高井底压力稳定性,但同时要注意避免低排量或大管径带来的携砂能力降低的问题。
(3) 温度和压力对井筒内CO2流体密度和黏度均有影响,但受温度影响更大,特别是CO2流体黏度与温度成反相关。在常规施工条件下,CO2流体黏度仅为0.08~0.25 mPa·s,携砂能力差,加之进入储层后易转变为超临界态,界面张力变为零,滤失量极大,不利于压裂扩展,易导致压裂施工失败。建议研制高效增稠剂和超低密度支撑剂以提高CO2流体携砂能力。
(4) CO2干法压裂过程中是否发生相态转变取决于井底温度,而CO2干法压裂过程中井底温度受注入温度影响最大,其次为注入排量和地温梯度,几乎不受油管内径的影响;在常规干法压裂过程中,CO2流体井底温度明显低于其临界温度,在井筒范围内不会发生相态转变,但在地温梯度较高井或较深井应用CO2干法压裂时可通过适当降低井口注入温度,避免发生相态转变而导致的井筒压力控制不稳定以及影响其携砂能力。
| [1] |
贾承造, 郑民, 张永峰. 中国非常规油气资源与勘探开发前景[J]. 石油勘探与开发, 2012, 39(2): 129-136. JIA C Z, ZHENG M, ZHANG Y F. Unconventional hydrocarbon resources in China and the prospect of exploration and development[J]. Petroleum Exploration and Development, 2012, 39(2): 129-136. |
| [2] |
刘合, 王峰, 张劲, 等. 二氧化碳干法压裂技术应用现状与发展趋势[J]. 石油勘探与开发, 2014, 41(4): 466-472. LIU H, WANG F, ZHANG J, et al. Fracturing with carbon dioxide:application status and development trend[J]. Petroleum Exploration and Development, 2014, 41(4): 466-472. |
| [3] |
邹才能, 张国生, 杨智, 等. 非常规油气概念、特征、潜力及技术——兼论非常规油气地质学[J]. 石油勘探与开发, 2013, 40(4): 385-399. ZOU C N, ZHANG G S, YANG Z, et al. Geological concepts, characteristics, resource potential and key techniques of unconventional hydrocarbon:on unconventional petroleum geology[J]. Petroleum Exploration and Development, 2013, 40(4): 385-399. |
| [4] |
卢义玉, 廖引, 汤积仁, 等. 页岩超临界CO2压裂起裂压力与裂缝形态试验研究[J]. 煤炭学报, 2018, 43(1): 175-180. LU Y Y, LIAO Y, TANG J R, et al. Experimental study on fracture initiation pressure and morphology in shale using supercritical CO2 fracturing[J]. Journal of China Coal Society, 2018, 43(1): 175-180. |
| [5] |
程宇雄, 李根生, 王海柱, 等. 超临界二氧化碳喷射压裂井筒流体相态控制[J]. 石油学报, 2014, 35(6): 1182-1187. CHENG Y X, LI G S, WANG H Z, et al. Phase control of wellbore fluid during supercritical CO2 jet fracturing[J]. Acta Petrolei Sinica, 2014, 35(6): 1182-1187. |
| [6] |
陈立强, 田守嶒, 李根生, 等. 超临界CO2压裂起裂压力模型与参数敏感性研究[J]. 岩土力学, 2015, 36(增刊2): 125-131. CHEN L Q, TIAN S C, LI G S, et al. Initiation pressure models for supercritical CO2 fracturing and sensitivity analysis[J]. Rock and Soil Mechanics, 2015, 36(S2): 125-131. |
| [7] |
ISHIDA T, AOYAGI K, NIWA T, et al. Acoustic emission monitoring of hydraulic fracturing laboratory experiment with supercritical and liquid CO2[J]. Geophysical Research Letters, 2012, 39(16): 1-6. |
| [8] |
郭建春, 曾冀. 超临界二氧化碳压裂井筒非稳态温度-压力耦合模型[J]. 石油学报, 2015, 36(2): 203-209. GUO J C, ZENG J. A coupling model for wellbore transient temperature and pressure of fracturing with supercritical carbon dioxide[J]. Acta Petrolei Sinica, 2015, 36(2): 203-209. DOI:10.3969/j.issn.1001-8719.2015.02.001 |
| [9] |
窦亮彬, 李根生, 沈忠厚, 等. 注CO2井筒温度压力预测模型及影响因素研究[J]. 石油钻探技术, 2013, 41(1): 76-81. DOU L B, LI G S, SHEN Z H, et al. Wellbore pressure and temperature prediction model and its affecting factors for CO2 injection well[J]. Petroleum Drilling Techniques, 2013, 41(1): 76-81. DOI:10.3969/j.issn.1001-0890.2013.01.015 |
| [10] |
赖力, 龙伟. 超临界CO2管道泄压过程中管内动态应力分布[J]. 油气储运, 2018, 37(3): 276-280. LAI L, LONG W. Distribution of dynamic stress on the supercritical CO2 pipeline in the process of its pressure relief[J]. Oil & Gas Storage and Transportation, 2018, 37(3): 276-280. |
| [11] |
KABIR C S, HASAN A R, KOUBA G E, et al. Determining circulating fluid temperature in drilling, workover, and well control operations[R].SPE 24581, 1992.
|
| [12] |
HASAN A R, KABIR C S. Aspects of wellbore heat transfer during two-phase flow[R]. SPE 22948-P4, 1994.
|
| [13] |
SPAN R, WAGNER W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa[J]. Journal of Physical and Chemical Reference Data, 1996, 25(6): 1509-1596. DOI:10.1063/1.555991 |
| [14] |
FENGHOUR A, WAKEHAM W A, VESOVIC V. The viscosity of carbon dioxide[J]. Journal of Physical and Chemical Reference Data, 1998, 27(1): 31-43. DOI:10.1063/1.556013 |
| [15] |
VESOVIC V, WAKEHAM W, OLCHOWY G, et al. The transport properties of carbon dioxide[J]. Journal of Physical and Chemical Reference Data, 1990, 19(3): 763-808. DOI:10.1063/1.555875 |
| [16] |
CHEN N H. An explicit equation for friction factor in pipe[J]. Industrial and Engineering Chemistry Research Fundamentals, 1979, 18(3): 296-297. DOI:10.1021/i160071a019 |


