2. 北京石油机械有限公司
2. Beijing Petroleum Machinery Co., Ltd
0 引言
由于海上石油平台工况不稳定,所以传统的旋流分离设备正逐渐暴露出一些弊端,主要包括应用条件限制性大、工况环境敏感性高和出口流体排放不佳等。针对旋流分离器结构特点,相关人员在优化混合来流分离状况方面做了大量工作。K.S.LIM和A.RAOUFI等[1-2]通过试验得出,渐缩式溢流口在不影响分离效率的同时,还能有效降低压力损失。G.E.KOUBA等[3]指出,优化倾斜入口位置和倾斜角度可使气液两相分层,实现预分离。R.HREIZ等[4]认为合理设计入口喷嘴参数能改变入口流型,进而优化分离器性能。赵立新和王庆锋等[5-6]研究了旋流分离器长度、主直径、溢流管和底流管尺寸对分离性能的影响。但这些研究仅局限于分离器某一部分结构,很少从液滴和气泡粒子角度来证实影响气液两相分离的本质。因此,有必要对传统旋流分离器中的相关影响因子做适当优化,并结合剪切旋转气流驱动下液滴的破碎规律来论证优化的合理性。
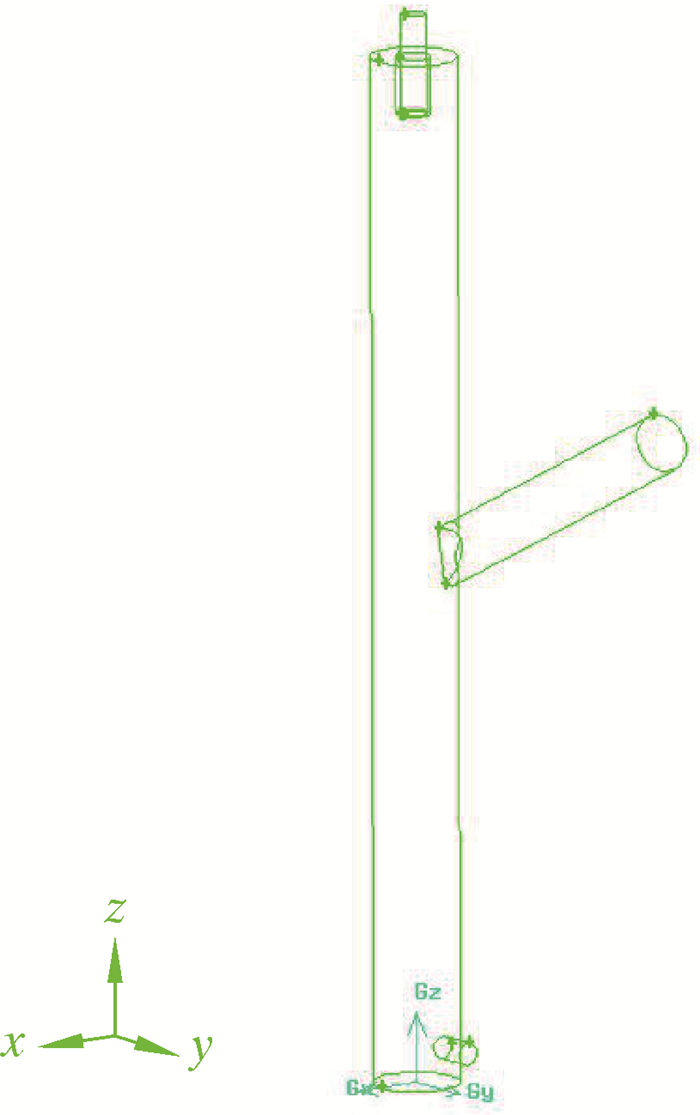
1 柱状气液旋流分离器数值模型经典式GLCC分离器是现在最常见的一类气液旋流分离器,如图 1所示。该经典模型在实践过程中常出现溢流口排气不彻底、底流口携气严重及分离效率不高等问题,因此难以胜任较苛刻的工况。
|
| 图 1 经典式GLCC分离器 Fig.1 Classic GLCC separator |
稳流式柱状旋流分离器与经典式分离器的主要区别之一在于其内部含有圆形稳流器,见图 2。圆形稳流器可稳定旋流器内部流场,克服经典式结构中向上排气能力不足及液相反出气的缺点。

|
| 图 2 稳流式GLCC分离器 Fig.2 Steady-flow GLCC separator |
1.1 初始参数及边界条件
混合来流均匀分布,且不可压缩,其中液滴黏度为0.001 5 Pa·s、密度为1 250 kg/m3,气相黏度为1.789 4×10-5 Pa·s、密度为1.225 kg/m3。气液旋流分离器初始尺寸见表 1。流体沿入口边界垂直流入分离器,入口边界设为速度入口,初始定常入口速度10 m/s,入口气相体积分数10%。溢流口和底流口边界为流动出口,流体流动按充分发展处理,固体壁面设置为无滑移边界。
| 参数名称 | 经典式 | 稳流式 |
| 筒体直径/mm | 60 | 60 |
| 筒体长度/mm | 720 | 360 |
| 溢流口直径/mm | 18 | 18 |
| 溢流口伸出长度/mm | 30 | 30 |
| 溢流口插入深度/mm | 40 | 40 |
| 底流口直径/mm | 15 | 15 |
| 入口尺寸/mm | ø40 | 15×25 |
| 入口高度/mm | 360 | 360 |
| 入口倾斜角/(°) | 27 | — |
| 稳流器直径/mm | — | 30 |
| 稳流器安装高度/mm | — | 40 |
1.2 网格划分与数值模拟方法
由于分离器局部结构的非规则性,无法整体生成结构化网格,所以为了保证网格质量,确保模型求解精度及降低计算成本,将分离器模型切分为多个部分,分别进行网格划分,即非规则结构部分采用四面体网格划分,规则结构部分采用六面体网格划分。在某些特殊部分附近加密网格,以提高计算准确性和收敛性。为在旋流器内形成兰金组合涡,反映旋流分离器在重力、离心力和其他体积力联合作用下的分离效果,在数值模拟中使用求解精度更高的RSM雷诺应力模型和Mixture模型。
2 SFS-GLCC分离器结构优化设计 2.1 经典式与稳流式GLCC分离器性能对比分离效率是衡量分离器分离性能的重要指标之一,基于质量理论将其定义如下:

|
(1) |
式中:ηm为分离效率,mg、minlet分别为溢流口和入口气相总质量,Qg、Ql、Qinlet分别为溢流口、底流口和入口混合物流量,Cg、Cl、Cinlet分别为溢流口、底流口和入口气相体积分数,F为分流比。
经典式与稳流式GLCC分离器性能对比见表 2。
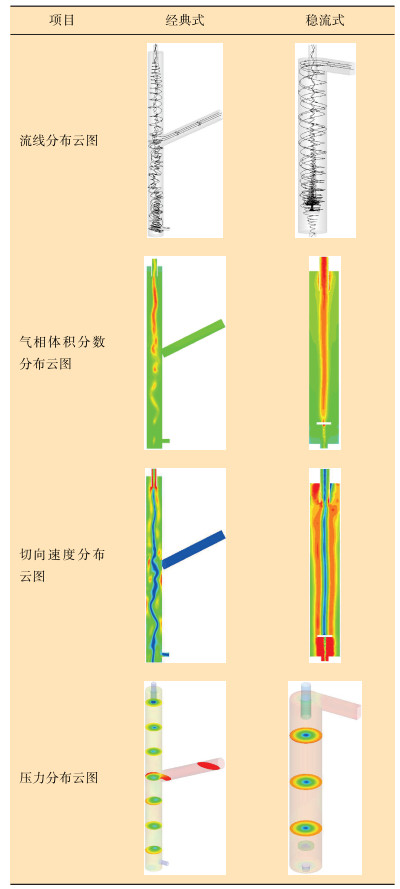
与带有圆形稳流器的稳流式柱状气液旋流分离器相比,经典式GLCC分离器明显有以下不足:①旋涡区流场较为紊乱,旋转气核与周围液相分界面不明显;②气体向轴心的运移能力不足,使空气柱的聚气能力下降,不利于空气柱中的气体向溢流口排出;③气核波动幅度大、不稳定,呈扭曲状,随着气核的旋转,气核与周围分散在液相中的气泡融合的同时也分裂出气泡释放到液相中。
对表 1的初始数据进行模拟求解,得出稳流式GLCC分离器的分离效率比经典式提高了9%。其主要原因为稳流器与入口管结构优化。
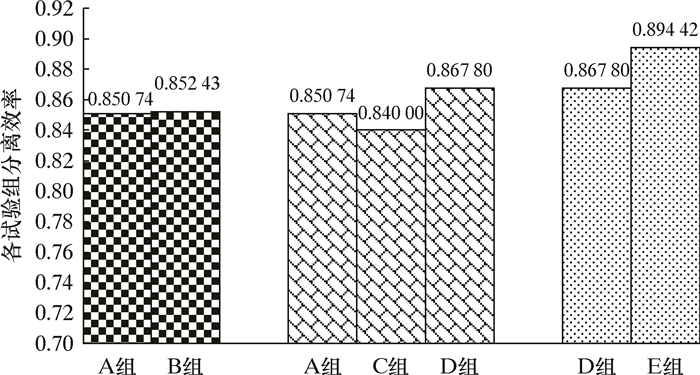
2.2 溢流管、入口和筒体形式为进一步提高分离器性能,基于附加圆形稳流器的稳流式GLCC分离器,依据溢流管形式,设置A、B对照试验组;根据入口形式,设置A、C、D试验组;依照筒体形式,设置D、E对照试验组,如表 3所示。各试验组对比见图 3。
|
| 图 3 溢流口、入口和筒体形式试验组对比 Fig.3 Comparison of test group in the form of gas outlet, inlet and cylinder |
2.2.1 溢流管形式
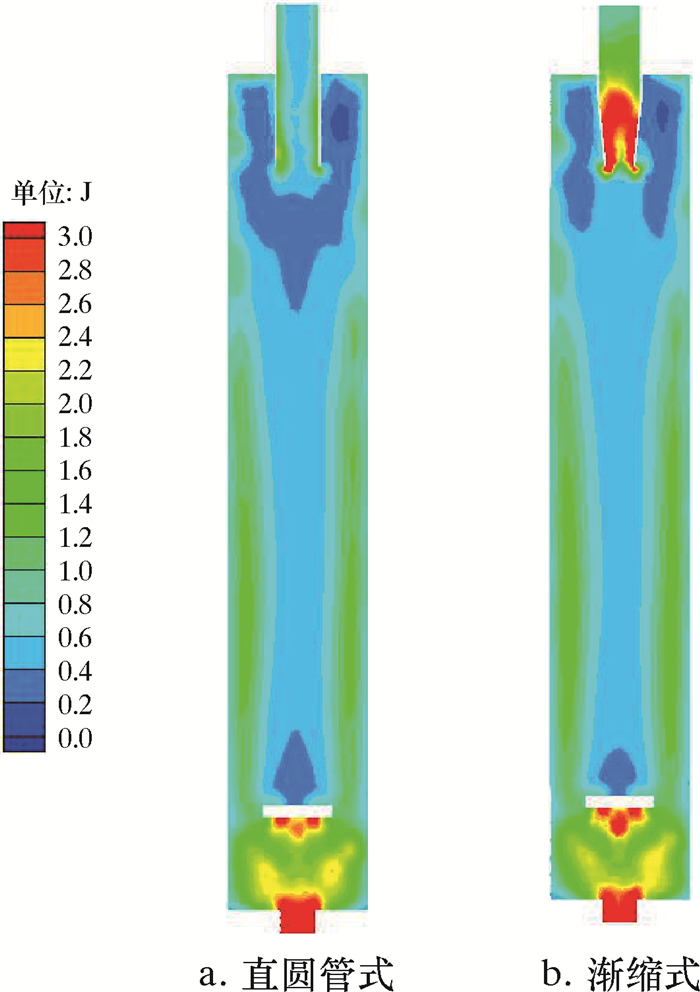
图 4为不同形式溢流管湍动能分布。由图 4可知,GLCC分离器湍动能较大区域主要集中在分离器底流口以及圆形稳流器下端。但若将溢流口形式变为渐缩式,由于锥段流体面积缩小,虽会增大轴向速度,但同时会导致溢流口湍动能急剧增大。溢流口湍动能过大会引起分离出的气相波动幅值加大,不利于气相沿溢流口逸出。
|
| 图 4 不同形式溢流管的湍动能分布 Fig.4 Turbulent kinetic energy distribution in different gas outlet forms |
相比于渐缩式溢流管,直管式溢流管在压力损失较小的情况下分离效率仅下降0.17%,两种形式溢流管对分离性能整体影响不大。综合考虑分离器制造加工难易程度与分离的实际效果,溢流管选用直管式较好。
2.2.2 入口形式入口的结构形式是混合流体在腔内实现旋转分离的关键,不同的入口形式会导致混合来流的运动形式、多相流型以及所受阻力等发生变化,以致影响气液两相的分离。本节将分别讨论切向直流、27°倾斜管流[7]和螺旋管流3类入口形式,分析它们对气液分离的影响。
G.E.KOUBA等[3]研究表明,入口流型呈现分层流将在很大程度上改善气液分离效果,扩大其应用范围。图 5为不同入口形式的入口流型。由图 5可知,当入口形式为螺旋管流时,由于离心力的作用,气液两相在入口管分层明显,有利于提高分离器的分离性能。螺旋管流式入口的分离效率比切向直管式入口的分离效率提高近2%,比倾斜管流式入口的分离效率提高近3%。因此,入口形式选用螺旋管流有助于气液两相的分离。
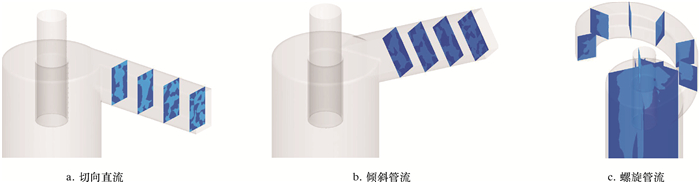
|
| 图 5 不同入口形式的入口流型 Fig.5 Inlet flow patterns for different inlet forms |
2.2.3 筒体形式
图 6为不同筒体形式GLCC分离切向速度分布。从图 6可知,锥式筒体的旋流分离器的切向速度高于直筒式旋流分离器,且腔体空间利用率较大,分离效率提高了近3%。这是因为锥式旋流分离能提高分离流体的旋转速度,达到强化离心力场的作用,质量相对较大的物质就会移至壁面,导致旋流器壁到轴心的压力逐渐递减,分离液在旋流器的停留时间就会延长,对于介质的分离起到很好的作用。
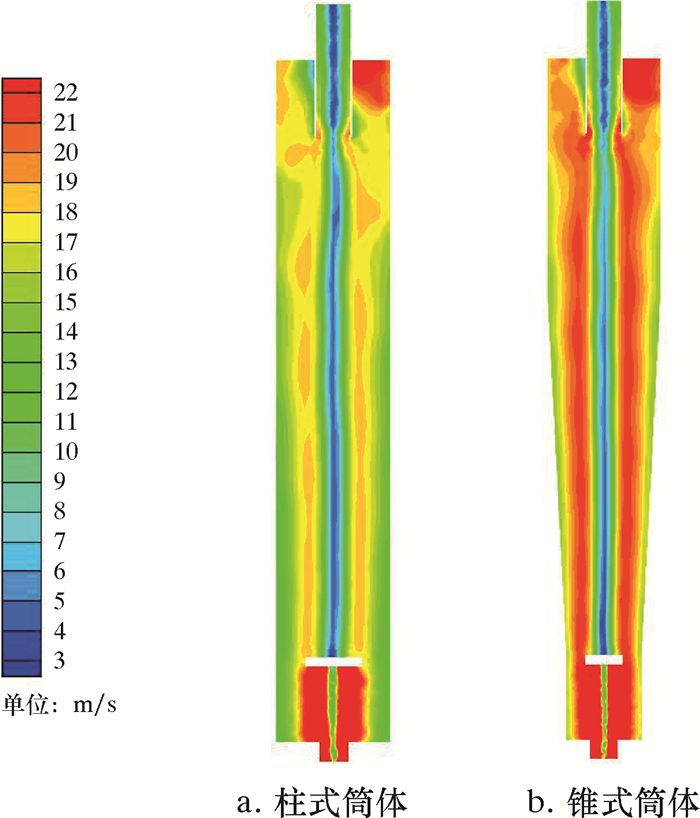
|
| 图 6 不同筒体形式GLCC分离器切向速度分布 Fig.6 Tangential velocity distribution of GLCC separators in different cylinder forms |
根据上述GLCC分离器结构形式的讨论分析,决定在分离器内部添加圆形稳流器,入口采用矩形截面、螺旋式结构形式,底流管与溢流管均使用直圆管,筒体采用渐缩式来构造一种新型GLCC分离器——稳流螺旋驱锥式气液旋流分离器,可简称为SFS-GLCC分离器,其具体结构如图 7所示。
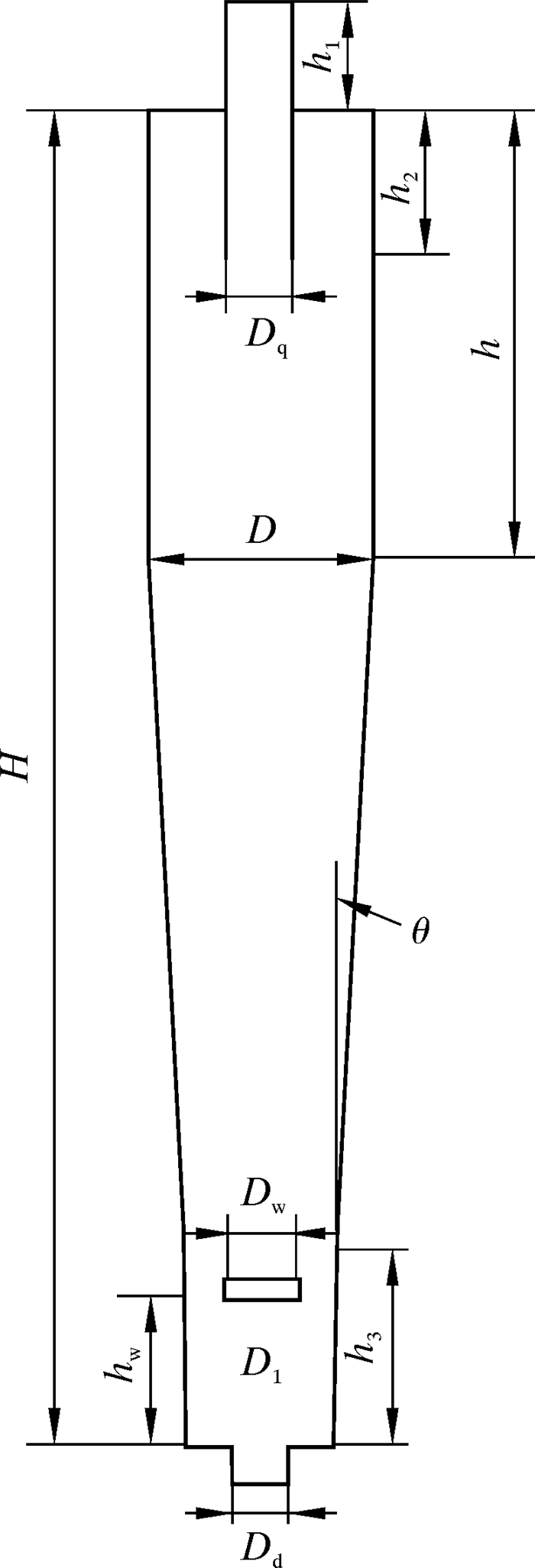
|
| 图 7 SFS-GLCC分离器结构示意图 Fig.7 SFS-GLCC separator |
2.3 SFS-GLCC分离器敏感性和适用性分析
为使SFS-GLCC分离器分离性能最优,基于内部流场特性,对该分离器各结构参数进行敏感性分析,优化后的参数见表 4。
| 参数名称 | 数值 |
| 主筒体直径D/mm | 60(D) |
| 主筒体长度h/mm | 240(4D) |
| 溢流口直径Dq/mm | 24(0.4D) |
| 溢流口伸出长度h1/mm | 30(0.5D) |
| 溢流口插入深度h2/mm | 48(0.8D) |
| 圆形稳流器直径Dw/mm | 20(0.5D1) |
| 螺旋入口公称直径DL/mm | 70(1.17D) |
| 螺旋入口螺距S/mm | 60(D) |
| 下部直筒段长度h3/mm | 50 |
| 中部渐缩段长度L/mm | 250(5D-h3) |
| 渐缩段下底直径D1/mm | 40(2D/3) |
| 分离器腔体总长度H/mm | 540(9D) |
2.3.1 入口速度v
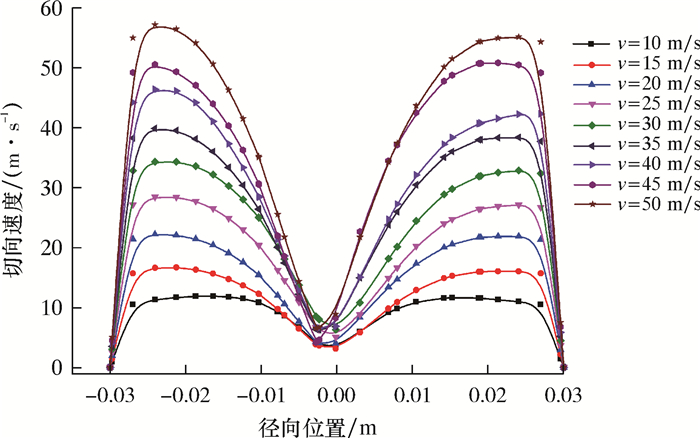
入口速度减小和增大均不利于分离效率的提高(见图 8)。因为离心分离需要一定的入口速度,若入口速度较低,混合来流在旋流腔内部无法形成足够旋转速度的涡流,使混合流体无法提供充足的动能供气液两相分离,导致分离不彻底而以混合方式从底流口流出;当入口速度过高时,气液混合相在旋流腔内部的切向速度增大(见图 9),易使液滴受到过大的剪应力作用而发生破碎,粒径变小会加大气液混合相的乳化程度,不利于分离,从而使分离效率降低。
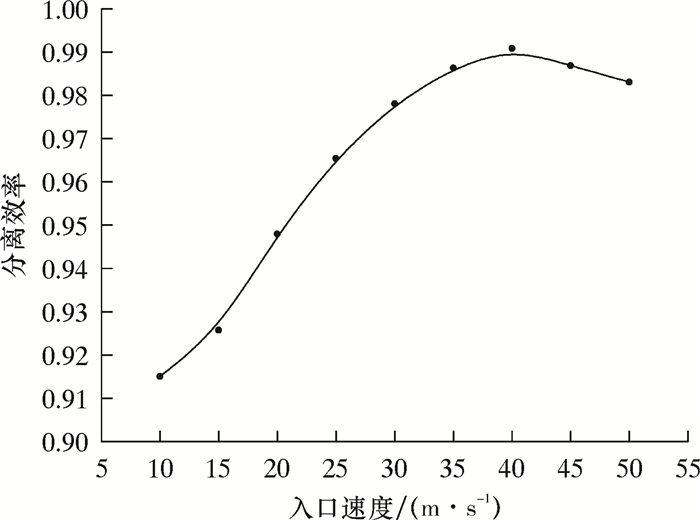
|
| 图 8 入口速度与分离效率的关系曲线 Fig.8 Effect of inlet velocity on separation efficiency |
|
| 图 9 不同入口速度下切向速度分布曲线 Fig.9 Tangential velocity distribution at different inlet velocities |
2.3.2 含气体积分数与分离器规格
为探究新型分离器在实际工程上的适用性、广泛性以及普及性,给现场工况提供参考和指导意见,本文针对不同尺寸规格、不同入口含气体积分数下的SFS-GLCC分离器进行了研究。S.WANG等[8]指出,GLCC分离器在不同应用工况下的公称直径一般在76.2~1 524.0 mm,因此所选SFS-GLCC分离器的规格应在此范围内。
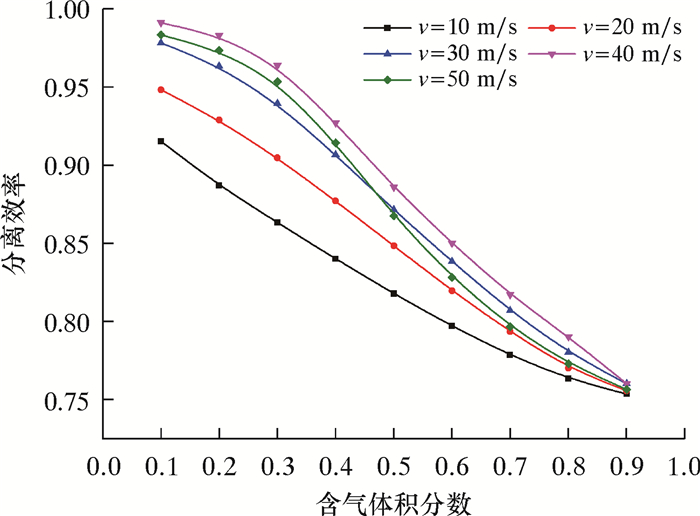
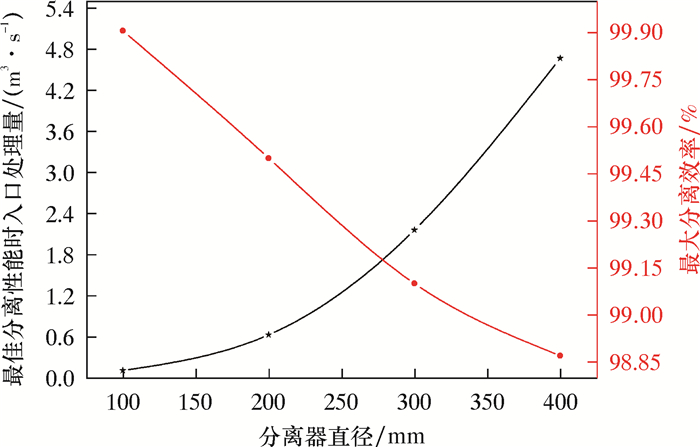
图 10显示,SFS-GLCC分离器的分离效率与入口含气体积分数呈负相关, 且在足够的入口速度下,该旋流器的分离效率可达到99.08%。结合图 11可知,SFS-GLCC分离器在不同应用工况下的适应性更强,应用范围更广,分离性能更高,能充分满足实际要求。
|
| 图 10 分离效率随含气体积分数的变化曲线 Fig.10 Effect of gas content on the separation efficiency |
|
| 图 11 不同规格SFS-GLCC分离器适用性曲线 Fig.11 Applicability curve of different specifications of SFS-GLCC separator |
3 剪切气流驱动下离心旋流场的液滴破碎
在气液旋流分离器中,液滴之间发生聚合,能显著提高分离器分离效率,但液滴破碎则不利于气液两相的分离,造成极大的资源浪费。本节以群体平衡模型分析SFS-GLCC分离器内部液滴在分离过程中的粒径分布规律为基础,结合Python建立的液滴破碎TAB判定模型,探究相应粒径的液滴在特定流场域下的形状变化和运动状态,并验证所构建的气液两相分离模型的可行性。分析过程中若无特殊说明,选用的SFS-GLCC分离器主筒体直径为60 mm,气液间的表面张力为0.02 N/m。
3.1 基于Python液滴破碎的TAB判定模型TAB模型是研究剪切气流驱动下液滴变形破碎的常用模型[9-11]。通常将TAB模型液滴表面的变形类比于弹簧振动,弹簧振动控制方程中弹簧的振动振幅ξ相当于液滴变形量,弹簧质量m等效于液滴质量,弹簧受到的外力F等效于液滴所受气动压力,弹簧阻尼力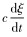
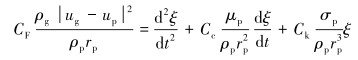
|
(2) |
令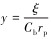
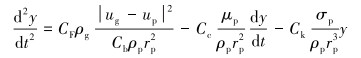
|
(3) |
式中:rp为未变形液滴的半径;Cb、CF、Cc和Ck均为无量纲常数。
由试验数据推导可知,CF=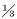
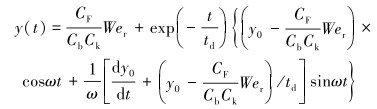
|
(4) |
式中: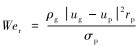
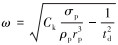
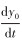
对式(2)进行简化,可推出液滴初始时刻的变形量为:
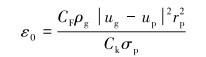
|
(5) |
则振动初始时刻液滴偏离距离如下:
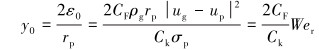
|
(6) |
故式(4)可简化为:
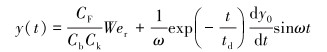
|
(7) |
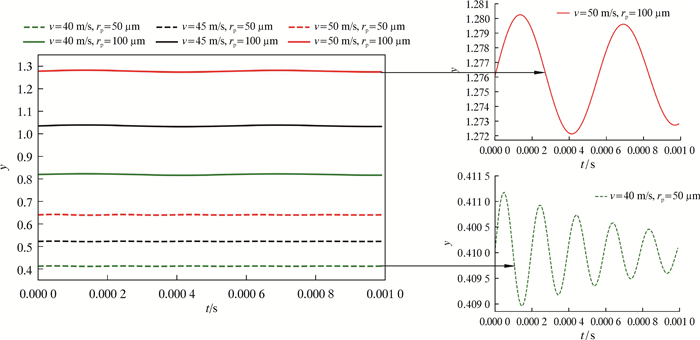
根据韦伯数、阻尼时间、振动频率计算公式及相应的特征参数,得出在不同偏离速度和粒径下,液滴偏离距离随时间的变化曲线,如图 12所示。
|
| 图 12 液滴偏离距离随时间的变化曲线 Fig.12 Droplet deviation distance versus time |
图 12主要显示了在液滴粒径100和200 μm情况下,不同偏离速度对液滴破碎变形的影响情况。当y≥1.0时,液滴破裂。
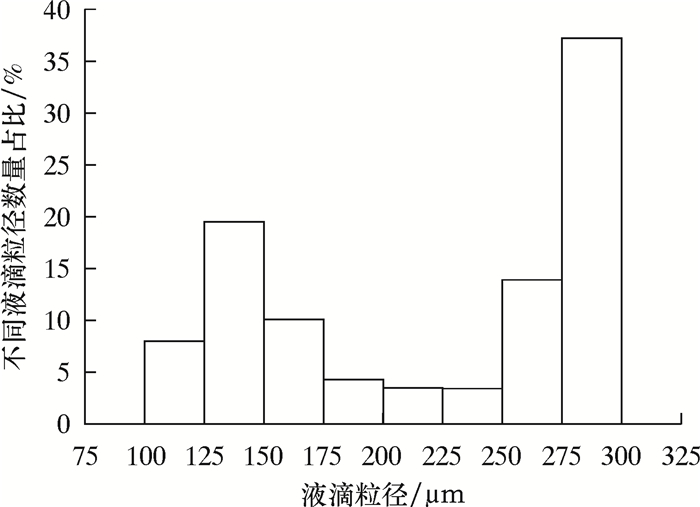
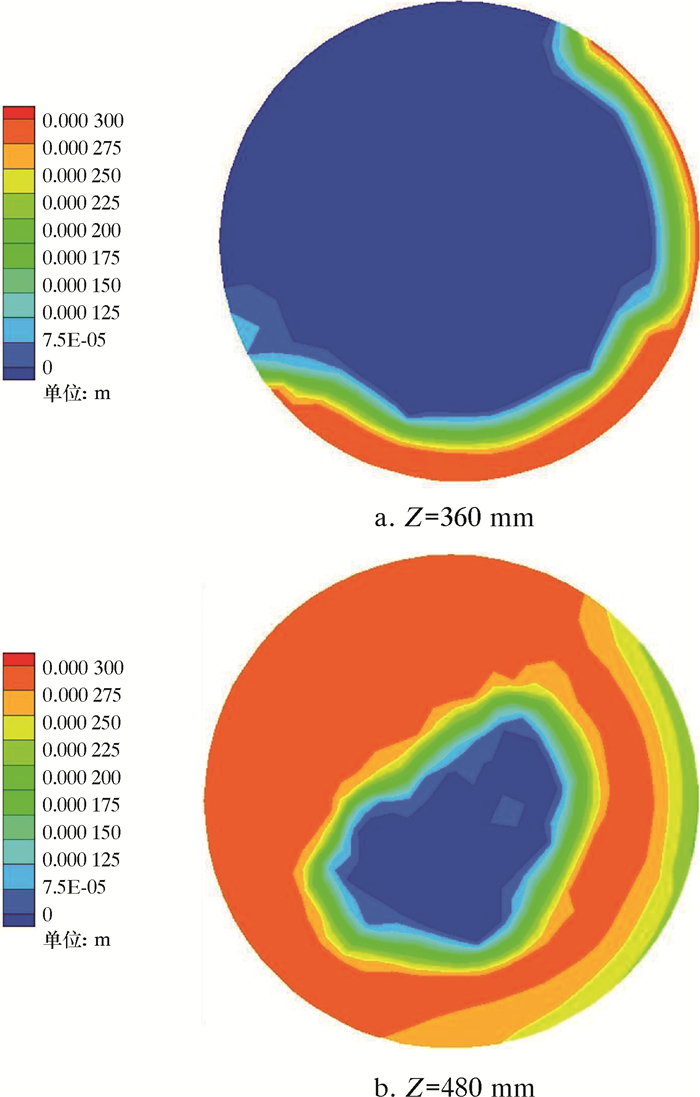
3.2 基于PBM的液滴粒径分布规律在分离过程中,采用图 8中的峰值入口流速40 m/s,定义液滴粒径范围为50~300 μm,且入口混合来流的初始液滴粒径设定为175 μm,以此来对整个SFS-GLCC分离器三维模型迭代求解。提取整个计算域空间内不同液滴粒径数量占比直方图,其分布如图 13所示。分离器Z=360、480 mm横截面上各粒径分布云图如图 14所示。
|
| 图 13 整个计算域内不同液滴粒径数量占比直方图 Fig.13 Histogram of the number of droplets with different sizes in the entire calculation domain |
|
| 图 14 分离器各横截面上的粒径分布云图 Fig.14 Particle size distribution of each cross section of the separator |
由图 14可知,在初始液滴粒径175 μm前后,均存在小粒径或大粒径液滴占比较大的情形,说明经螺旋轨迹进口流入分离器腔的液滴发生了明显的聚合和破碎现象。除此之外,分离器内的液滴粒径在75~100 μm范围内的数量占比极小,近乎为0,整个流场域内的粒径基本不会小于100 μm。
当SFS-GLCC分离器入口速度为40 m/s时,由图 9可知分离器内液滴所受的最大切向速度接近47 m/s。再结合图 12中TAB模型液滴破碎的判定规律,当分离器入口速度为40 m/s时,粒径100 μm以下的液滴不会破碎。这与PBM模型求解的分离器内液滴粒径的分布规律很接近。同理可知,当SFS-GLCC分离器入口速度为45 m/s时,粒径100 μm以下的液滴依旧不会破碎。因此,下面取粒径大于100 μm的液滴来探讨它们的形状变化和运动状态。
3.3 剪切旋转气流下液滴变形、破碎与聚结气液旋流分离器中的液滴一般包含变形、破碎和聚结等过程。由于三维旋流分离流场较为复杂,为便于模拟液滴在剪切旋转气流下的变形破碎过程并降低计算成本,选取利用UDF描述的SFS-GLCC分离器中Z=360 mm横截面上切向速度、径向速度场分布的二维模型,同时定义距离圆心水平方向5.50、11.25、17.50、23.75以及29.50 mm五个排序为①、②、③、④、⑤的液滴颗粒分布在该二维模型上,选用液滴粒径为150 μm。
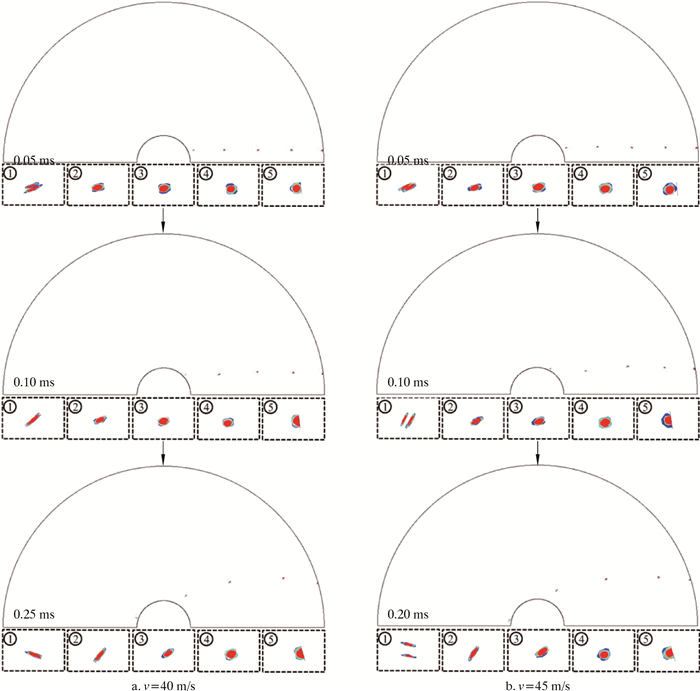
3.3.1 入口速度选取图 8中分离效率最高的拐点入口速度40 m/s,以及开始出现分离效率下行的入口速度45 m/s进行对比分析,结果如图 15所示。从图 15可见,速度40 m/s时对应的速度场液滴有破碎趋势,但并不会呈现永久破碎过程,若将入口速度增大至45 m/s,则液滴发生明显的分裂破碎。
|
| 图 15 不同入口速度下各液滴的变形、破碎过程 Fig.15 Deformation and crushing process of each droplet at different inlet velocities |
3.3.2 液滴粒径
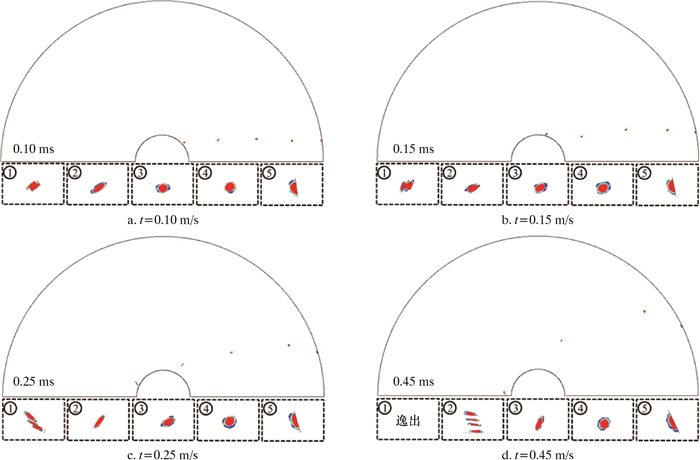
仍选择图 8中分离效率最高的拐点入口速度40 m/s,对粒径为150和200 μm的液滴进行对比分析,结果如图 15a和图 16所示。较大速度梯度和湍流强度的共同作用会增大大液滴破碎概率,部分破碎后的小液滴易随径向气流再次进入内旋流,降低分离效率。
|
| 图 16 200 μm粒径液滴的变形、破碎过程 Fig.16 Deformation and crushing process of droplets with a particle size of 200 μm |
综上所述,在旋流分离器气柱边缘和器壁附近,切向速度变化起伏大,而在其他区域沿径向分布则较为平缓。这会导致气柱和器壁周边有很高的速度梯度,混合来流处于动量迅速转换的强剪切层中会产生很大雷诺剪切应力,降低液滴稳定性。因此,SFS-GLCC分离器气柱边缘和器壁附近更易发生液滴变形和破碎。
SFS-GLCC分离器以40 m/s的入口速度进行分离时,液滴破碎的临界粒径在150~200 μm;而对于45 m/s的入口速度,液滴破碎的临界粒径在100~150 μm。因此,入口速度40 m/s时液滴稳定性更强。这不仅与TAB模型求解结果接近,也与上文所得最佳入口分离速度结论相符。
4 结论(1) SFS-GLCC分离器的螺旋式入口能促进气液两相分层,使入口流型呈现团状流;稳流器可避免底流口夹带气和溢流口排气不彻底;锥式筒体能提高流体旋转速度,延长分离液腔内停留时间。
(2) 基于Python液滴破碎的TAB判定模型和剪切气流驱动下旋流器内液滴破碎模拟,得到如下结论:SFS-GLCC分离器气柱边缘和器壁附近切向速度变化起伏大,具有很高的速度梯度,位于该区域的液滴稳定性较低,更易变形和破碎;入口速度为40 m/s时液滴稳定性更强。
(3) 剪切旋转气流下液滴的运动变形状况不仅与TAB判定模型求解结果相近,且符合SFS-GLCC分离器入口速度与分离效率之间的变化规律,说明所构建的气液两相分离模型具有可行性。
(4) 研究结果可为气液旋流分离器的优化设计提供一定的借鉴和参考。
| [1] |
LIM K S, KIM H S, LEE K W. Characterization of the collection efficiency for a cyclone with different vortex finder shapes[J]. Journal of Aersol Science, 2004, 35(6): 743-754. DOI:10.1016/j.jaerosci.2003.12.002 |
| [2] |
RAOUFI A, SHAMS M, FARZANEH M, et al. Numerical simulation and optimization of fluid flow in cyclone vortex finder[J]. Chemical Engineering and Processing:Process Intensification, 2008, 47(1): 128-137. DOI:10.1016/j.cep.2007.08.004 |
| [3] |
KOUBA G E, SHOHAM O, SHIRAZI S. Design and performance of gas-liquid cylindrical cyclone separators[C]//Proceedings of the BHR Group 7th International Meeting on Multiphase Flow, Cannes, France: [s.n.]. 1995: 307-327.
|
| [4] |
HREIZ R, LAINE R, WU J, et al. On the effect of the nozzle design on the performances of gas-liquid cylindrical cyclone separators[J]. International Journal of Multiphase Flow, 2014, 58: 15-26. DOI:10.1016/j.ijmultiphaseflow.2013.08.006 |
| [5] |
赵立新, 宋民航, 蒋明虎, 等. 柱状气液分离器长径比优选及实验研究[J]. 化工机械, 2013, 40(1): 30-33. ZHAO L X, SONG M H, JIANG M H, et al. Optimization and experimental study on gas-liquid[J]. Chemical Engineering & Machinery, 2013, 40(1): 30-33. DOI:10.3969/j.issn.0254-6094.2013.01.008 |
| [6] |
王庆锋, 李凯, 郝帅, 等. MVR系统中管柱式气液旋流分离器性能研究[J]. 化工进展, 2016, 35(增刊2): 87-91. WANG Q F, LI K, HAO S, et al. Performance study of the gas-liquid column cyclone in MVR system[J]. Chemical Industry and Engineering Progress, 2016, 35(S2): 87-91. |
| [7] |
GOMEZ L E, MOHAN R S, SHOHAM O, et al. State-of-the-art simulator for field applications of gas-liquid cylindrical cyclone separators[C]//SPE Annual Technical Conference.[s.l.]: SPE, 1999.
|
| [8] |
WANG S, MOHAN R, SHOHAM O, et al. Optimal control strategy and experimental investigation of gas/liquid compact separators[J]. SPE Journal, 2002, 7(2): 170-182. DOI:10.2118/78270-PA |
| [9] |
ZEOLI N, GU S. Numerical modelling of droplet breakup for gas atomization[J]. Computational Materials Science, 2006, 38(2): 282-292. DOI:10.1016/j.commatsci.2006.02.012 |
| [10] |
PATTERSON M A. Modeling the effects of fuel injection characteristics on diesel combustion and emissions[D]. Madison: University of Wisconsin, 1997.
|
| [11] |
TRINH H P. Modeling of turbulence effect of liquid jet atomization[D]. Huntsville: University of Alabama, 2004. http://www.researchgate.net/publication/253465489_Modeling_of_turbulence_effect_on_liquid_jet_atomization
|