2. 中国石油大学(北京)
2. China University of Petroleum(Beijing)
0 引言
近年来我国对海洋石油开采的力度在不断加大,海洋柔性管缆作为连接海上作业平台与海底装置的重要油气输送通道,其安全可靠性分析和辅助附件设计变得十分关键。由于海洋工况复杂,较长的海洋柔性管缆在海洋环境载荷下极易发生过度弯曲,进而产生应力集中导致管缆破坏。限弯器是一种由聚氨酯橡胶制成的圆筒形节式辅助性构件,由若干形状尺寸相同的限弯节组合而成,其主要作用是防止管道发生过大的弯曲变形而发生破坏,保证管道最小弯曲半径在合理范围内,一般作用在静态环境下。
目前,国内外针对限弯器研究的文献资料较少,API RP 17L2中提出了两种构型限弯器,并对其设计条件、材料选择和载荷工况等进行了说明[1]。安世居等[2]对限弯器结构设计、材料选择和计算分析进行了概述。孙元鹏[3]在只考虑重力载荷的作用下对API标准中两种构型限弯器进行分析计算并对比。王翎羽和管成飞等[4-5]分别对限弯器结构进行了优化设计。W.H.WHITEFIELD[6]提出了一种适用于不同半径管道的限弯器。T.PERSSON[7]设计了一种新型限弯器。本文考虑聚氨酯材料超弹性特性,研究了不同本构模型与不同温度作用下限弯器对柔性管缆曲率半径的影响。
1 限弯器结构设计选取美国石油协会API RP 17L2规范中提出的典型互锁式限弯器进行建模与非线性分析,其基本结构如图 1所示。限弯器设计主要依据脐带缆特征信息及工况环境,脐带缆信息及工况参数如表 1所示。

|
| 图 1 典型限弯器结构剖面图 Fig.1 Sectional view of a typical bend restrictor structure |
| 参数名称 | 数值 |
| 脐带缆外径/mm | 150±3 |
| 脐带缆拉伸刚度/(N·m) | 5.27×108 |
| 脐带缆弯曲刚度/(kN·m2) | 11.329 |
| 脐带缆最小弯曲半径/m | 3 |
| 工作弯矩/(kN·m) | 1 |
| 海水温度/℃ | 0~20 |
根据参考文献[8]计算限弯器等效厚度。限弯器的锁合半径可以根据柔性管缆的许用最小弯曲半径确定。一般情况下,取柔性管缆最小弯曲半径的1.5倍作为弯曲的极限半径。假设限弯器锁合半径为:
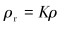
|
(1) |
式中:ρr是限弯器的锁合半径;K是安全系数,K由设计者设定,一般要求K≥1.5。
将限弯器等效为各向同性的线性材料,则材料力学公式为:
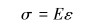
|
(2) |
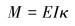
|
(3) |
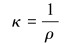
|
(4) |
式中:κ是曲率,E是弹性模量,I是横截面惯性矩,EI为弯曲刚度。
柔性管缆和限弯器的组合弯曲刚度为:
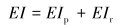
|
(5) |
式中:EIp是柔性管缆弯曲刚度,EIr是限弯器弯曲刚度。
在外力作用下,限弯器与柔性管缆组合系统的实际本构方程为:
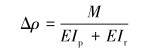
|
(6) |
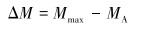
|
(7) |
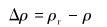
|
(8) |
式中:Mmax是柔性管缆所受到的最大弯矩,MA是限弯器与柔性管缆组合时所受到的弯矩。
限弯器横截面惯性矩可表示为:
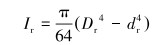
|
(9) |
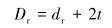
|
(10) |
式中:Ir是简化的限弯器横截面惯性矩,Dr是简化的限弯器外径,dr是简化的限弯器内径,t是限弯器的等效壁厚,联立以上方程即可求得限弯器的等效厚度t。
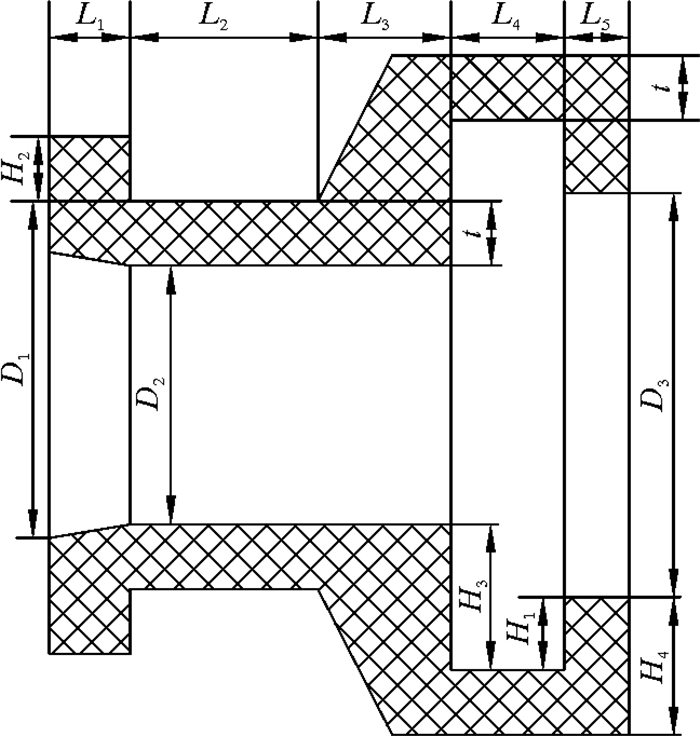
在限弯器的设计过程中,除了要考虑相邻两节子结构之间的几何适配性外,还要考虑结构的承载能力。图 2给出了限弯器需要设计的相关结构参数。为了保证限弯功能,这些几何参数之间存在一定的几何关系。限弯器自主设计变量包括图中H2、D2、L1、L2、L4、t以及D1、H1、D3、L5的设计余量δ0、δ1、δ2、δ3。限弯器壁厚根据等效壁厚t进行设计,参数之间具体几何关系见表 2。
|
| 图 2 限弯器结构参数 Fig.2 Bend restrictor structure parameters |
| 几何参数 | 计算公式 |
| D1 | D1=D2+δ0 |
| H1 | H1=H2+δ1 |
| D3 | D3+D2+2t+δ2 |
| H3 | 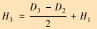 |
| L5 | L5=L2+L1-L4-δ3 |
| H4 | H4=H1+t |
2 数值模型 2.1 网格划分及边界条件设置
限弯器模型尺寸较长,加工制造成本较高,并且管缆为柔性材料,在外载荷作用下其形状会发生不规则变化。由于在变化过程中管缆发生大变形及管缆与限弯器间出现接触非线性,所以目前难以建立管缆与限弯器耦合理论模型进行求解,本文主要采用ABAQUS有限元软件对其进行数值分析。
建立如图 3所示三维完整模型。为简化计算,采用C3D8R实体单元进行网格划分。管缆与弯曲限制器接触关系设置为面面接触,采用小滑移条件,弯曲限制器之间接触关系设置为通用接触,摩擦因数均为0.2。在模拟过程中,管缆与限弯器会产生大变形情况,因此采用显示动力学方法进行分析。管缆Z轴正方向端部设置为固定约束,另一端施加沿Y轴负方向、大小为1 000 N·m的弯矩。限弯器Z轴正方向端部限制沿Z轴方向移动和沿X、Y轴方向转动,另一端设置为自由状态。

|
| 图 3 限弯器数值模型 Fig.3 Numerical model of the bend restrictor |
2.2 限弯器材料本构模型
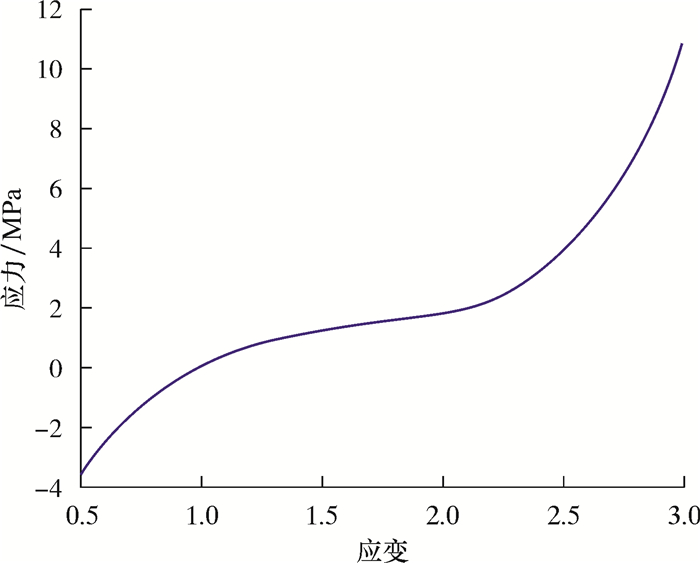
限弯器一般选用聚氨酯弹性体进行制造加工,该材料属于一种介于橡胶和塑料之间的高分子合成材料,会表现出明显的大变形非线性黏弹性力学行为。为了方便计算,在物理建模与实际应用中一般将其等效为超弹性模型进行处理。聚氨酯超弹性体具有不可压缩特性,在定义弹性模量与泊松比进行计算时仅适用于小变形范围内,在计算大变形时一般可采用应变势能函数来表示其本构关系。图 4为超弹性体在单轴应力状态下大致的应力-应变关系。从图 4可见,其应力-应变关系呈现S形趋势。
|
| 图 4 超弹性体的应力-应变关系曲线 Fig.4 Stress-strain curve of the hyperelastic body |
在连续介质力学中,假设聚氨酯材料为各向同性的超弹性材料,应变能密度函数用变形张量中3个不变量的一个或多个表示。由于近几年商业软件的快速发展,使得模拟超弹性材料三维应力及大变形成为可能。本文根据刘高冲[9]所提供的本构模型参数,选用表 3超弹性本构模型进行数值模拟。
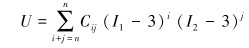
|
(11) |
| 本构模型 | 应变能密度函数表达式 |
| Mooney-Rivlin | U=C10(I1-3)+C01(I2-3) |
| Polyfit | U=C10(I1-3)+C01(I2-3)+C20(I1-3)2 |
| Ogden | 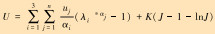 |
| Yeoh | U=C10(I1-3)+C20(I1-3)2+C30(I1-3)3 |
3 计算结果分析 3.1 本构模型及曲率半径
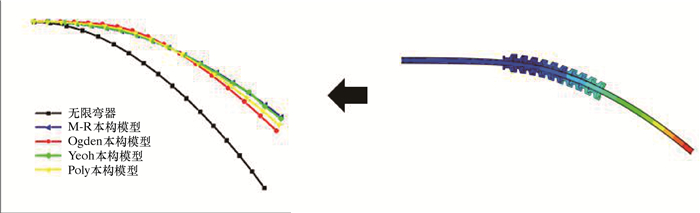
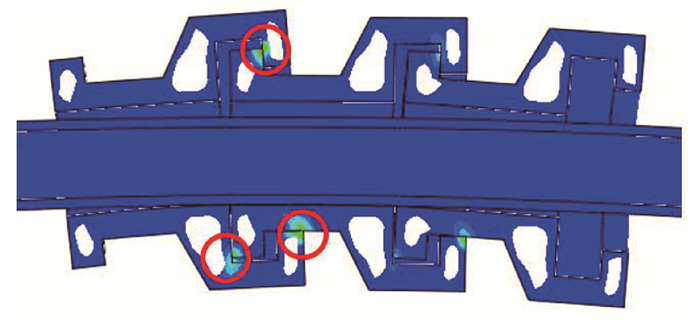
为了便于表示管缆在外载荷作用下的弯曲情况,运用最小二乘法沿柔性管轴向路径进行拟合,可以得到管缆弯曲程度相关形态曲线,如图 5所示。从图 5可见,没有安装限弯器管缆的弯曲程度明显大于安装限弯器管缆的弯曲程度,采用不同本构模型限弯器的管缆形态整体趋势相似,但仍存在区别。限弯器接触应力云图如图 6所示。由图 6可知,在限弯器弯曲过程中,某些部位容易发生应力集中从而导致限弯器变形。因此在对主要发生应力集中的部位设计时应使用圆角进行过渡。
|
| 图 5 外载荷作用下柔性管形态曲线 Fig.5 Flexible cable shape curve under external load |
|
| 图 6 限弯器接触应力云图 Fig.6 Contact stress of the bend restrictor |
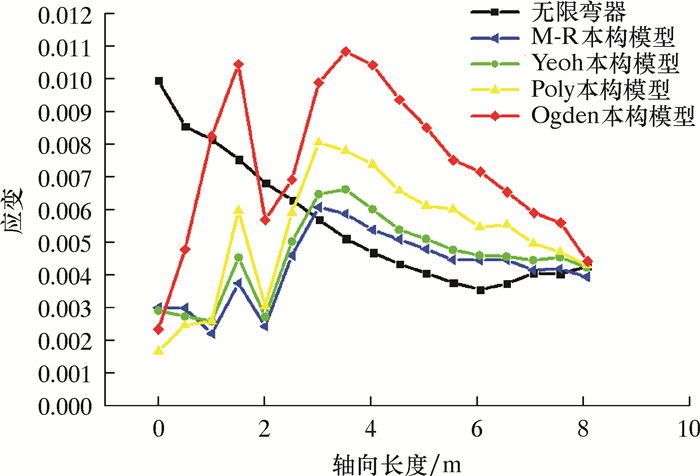
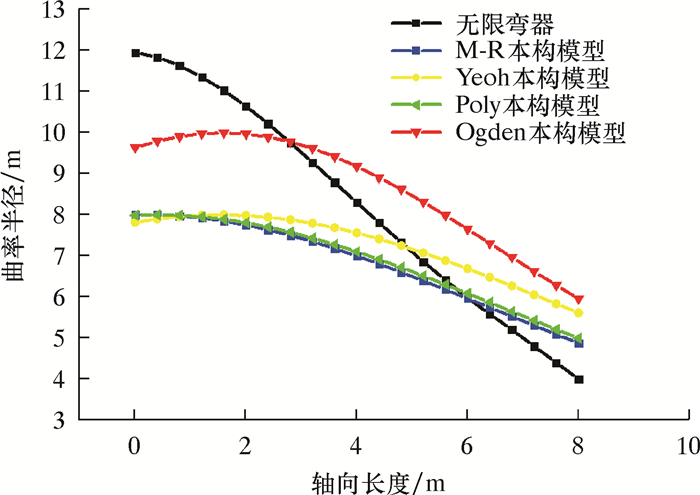
管道轴向应变如图 7所示。由图 7可知,在没有限弯器情况下管缆沿轴向应变逐渐减小,最大、最小应变分别为0.010 0和0.004 3。安装限弯器后,在1 600 mm应变会有一个突变,随后沿轴向先增大后减小,其原因是在3 000~5 000 mm部分管道与限弯器接触,此时产生的接触应力使限弯器发生较大的应变。管道轴向曲率半径如图 8所示。由图 8可知,限弯器曲率半径沿轴向长度逐渐减小,由于设计弯曲半径时需考虑安全系数(K=1.5),没有安装限弯器时管缆最小曲率半径为4.0 m,小于在安全系数下最小曲率半径4.5 m,不符合要求。安装限弯器管缆最小曲率半径范围4.9~6.0 m,管缆最小曲率半径均大于在安全系数下最小曲率半径。这说明该限弯器对柔性管缆可起到一定保护作用。从图 7和图 8中可以看到:采用Ogden本构模型所得结果与其余本构模型存在较大差异,在管道长度为1 600和4 000 mm时采用Ogden本构模型的应变分别为0.010 5和0.011 0,均大于不安装限弯器时管道最大应变,因此在对限弯器进行仿真模拟时,选用Ogden本构模型所得结果较为保守。
|
| 图 7 管道轴向应变 Fig.7 Axial strain of pipe |
|
| 图 8 管道轴向曲率半径 Fig.8 Axial curvature radius of pipe |
3.2 限弯器数量/工作温度与曲率半径的关系
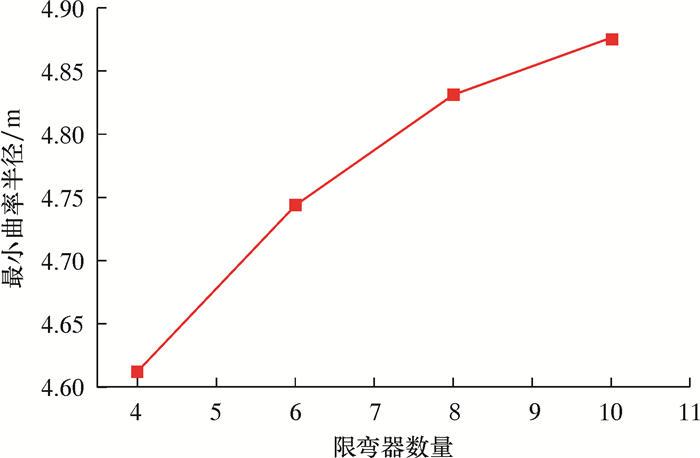
限弯器数量对管缆最小曲率半径也存在影响,本文使用Mooney-Rivlin本构模型分别计算了不同数量限弯器下管缆的最小曲率半径。如图 9所示,随着限弯器数量的增加,管缆最小曲率半径也增加,并且最小曲率半径增加的幅度也随之减缓。因此,在实际工程应用中,应根据需求计算出相应的限弯器数量,这样,既可以减少相应工作量,也可以节约成本。
|
| 图 9 限弯器数量不同时的最小曲率半径 Fig.9 Minimum bending radius under different number of bend restrictors |
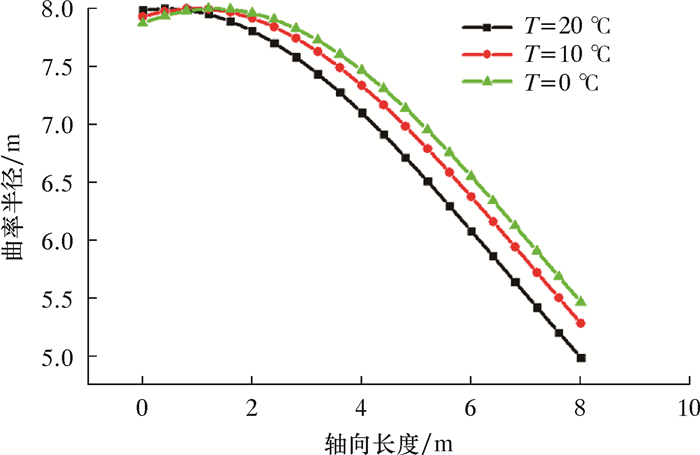
聚氨酯弹性体在变温作用下会有橡胶向玻璃态转变的过程,材料会出现硬化现象,因此聚氨酯材料性能对于温度变化存在一定敏感性。在工作过程中,脐带缆管内液压油工作温度范围为30~70 ℃,海水温度即电缆外表面温度范围设为0~10 ℃[10]。本文将引用严永明[11]在低温试验下拟合出橡胶Mooney-Rivlin本构模型关于温度的函数表达式,即式(12)和式(13),分别得出3组温度对柔性软管曲率半径的影响。如图 10所示,海水温度由0 ℃增加至20 ℃过程中,柔性管缆曲率半径逐渐减小。由于在升温过程中,橡胶材料刚性逐渐减小,塑性增大,使得限弯器延展性变得更强[12-13],限弯作用下降。因此在安装限弯器时可考虑采取一定的隔热措施,这样可增强对管缆的限弯效果。
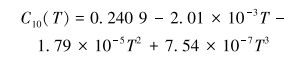
|
(12) |

|
(13) |
|
| 图 10 不同温度下沿管道轴向曲率半径变化 Fig.10 Variation of the curvature radius along pipe at different temperatures |
4 结论
本文利用材料力学计算出限弯器等效厚度,通过其结构之间的几何关系确定限弯器各结构尺寸。由于理论模型无法考虑限弯器材料超弹性特性与工作过程中大变形和接触非线性,所以采用有限元软件分析不同超弹性本构模型限弯器对管缆曲率半径的影响,得到在限弯器作用下管缆应变和曲率半径沿轴向的变化情况。经过分析得出以下结论:
(1) 安装限弯器时管缆最小曲率半径为4.90~6.00 m,符合安全工作要求。采用Ogden本构模型管缆最大应变为0.011,与其他本构模型存在较大差异,因此在对限弯器材料仿真模拟时采用Ogden本构模型获得数据较为保守。
(2) 限弯器数量对管缆最小曲率半径存在影响,通过计算得到限弯器数量由4个增加至10个时,其最小弯曲半径从4.61 m增加到4.87 m,且增长趋势逐渐减缓。
(3) 由于聚氨酯属于一种高分子聚合物,它的力学性能会随着温度的改变而发生变化,考虑限弯器工作温度范围,分别选取3组温度(0、10和20 ℃)进行计算,最小曲率半径分别为5.40、5.25和5.00 m。随着温度的升高,由于聚氨酯材料塑性增加,使得限弯器作用逐渐减小,管道曲率半径也随之减小。因此,在安装限弯器时一定要考虑环境温度,增加相应的隔热措施有助于增强限弯效果。
| [1] |
American Petroleum Institute. Recommended practice for flexible pipe ancillary equipment: API RP 17L2[S]. Washington: API Publishing Services, 2010.
|
| [2] |
安世居, 杨强, 白海洋, 等. 柔性软管弯曲限制器的设计[J]. 油气储运, 2016, 35(5): 551-554. AN S J, YANG Q, BAI H Y, et al. Design of bend restrictor for flexible pipes[J]. Oil and Gas Storage and Transportation, 2016, 35(5): 551-554. |
| [3] |
孙元鹏.深海柔性立管弯曲限制器的非线性力学分析[C]//第十八届中国海洋(岸)工程学术讨论会论文集(上).北京: 海洋出版社, 2017. SUN Y P. Nonlinear mechanical analysis of deep sea flexible riser bend limiter[C]//Proceedings of the 18th China Ocean (Ashore) Engineering Symposium (Part 1). Beijing: China Ocean Press, 2017. |
| [4] |
王翊羽, 梁威, 白海洋.海洋复合软管弯曲限制器: 201520446809.7[P].2015-11-04. WANG Y Y, LIANG W, BAI H Y. Marine composite hose bending limiter: 201520446809.7[P]. 2015-11-04. |
| [5] |
管成飞, 翟以军, 郭朝阳, 等.一种新型弯曲限制器: 206117026 U[P]. 2017. GUAN C F, ZHAI Y J, GUO C Y, et al. A new type of bending limiter: 206117026U[P]. 2017. |
| [6] |
WHITEFIELD W H. Variable radius vertebra bend restrictor: 2010228295[P]. 2009.
|
| [7] |
PERSSON T. Bending restrictor assem bly for use with a pipeline section: 8562255[P]. 2013.
|
| [8] |
谢宗伯.海洋柔性管缆弯曲限制器设计与制造技术研究[D].大连: 大连理工大学, 2017. XIE Z B. Research on design and manufacturing for bend limiter of marine flexible risers and umbilicals[D]. Dalian: Dalian University of Technology, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10141-1017823343.htm |
| [9] |
刘高冲.聚氨酯弹性体静动态力学性能及本构关系的研究[D].太原: 太原理工大学, 2017. LIU G C. Study on the mechanical properties and constutive of polyurethane elastomer under static/dynamic conditions[D]. Taiyuan: Taiyuan University of Technology, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10112-1017832288.htm |
| [10] |
李秀婧, 高欢, 刘骥. 脐带缆温度场与载流量分析计算[J]. 哈尔滨理工大学学报, 2014, 19(2): 85-89. LI X J, GAO H, LIU J. Analysis on temperature field and ampacity of umbilical cable[J]. Journal of Harbin University of Science and Technology, 2014, 19(2): 85-89. DOI:10.3969/j.issn.1007-2683.2014.02.016 |
| [11] |
严永明.低温环境下橡胶材料超弹性本构模型探究[D].秦皇岛: 燕山大学, 2016. YAN Y M. Research on superelastic constitutive model of rubber materials in low temperature environment[D]. Qinhuangdao: Yanshan University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10216-1016764013.htm |
| [12] |
VAZ M A, DE LEMOS C A D, CAIRE M. A nonlinear analysis formulation for bend stiffeners[J]. Journal of Ship Research, 2007, 51(3): 250-258. |
| [13] |
刘新福, 刘春花, 綦耀光. 煤层气井排采系统有杆泵运行特性分析[J]. 机械工程学报, 2017, 53(8): 195-200. LIU X F, LIU C H, QI Y G. Operating performance of sucker rod pump for the pumping system in coalbed methane wells[J]. Journal of Mechanical Engineering, 2017, 53(8): 195-200. |


