2. 成都工业学院
2. Chengdu Technological University
0 引言
页岩气是一种非常规性的重要能源,存储量巨大[1]。但页岩气储层渗透性极低,拥有低孔性的物性特征,因此水平井技术成为现代深层页岩气开发的重要手段。如何在提高页岩钻井效率的同时满足最佳的井底清岩效果,仍然是水平井钻井工程急需解决的问题。
PDC钻头井底流场的研究普遍采用计算流体力学(CFD)方法。R.CROUSE等[2]在1985年率先采用数值模拟方法对井底流场在理想流体情况下的奈维斯托克(N-S)方程进行求解,得出了PDC钻头的流场模拟结果。黄红梅等[3]通过对井底湍流流场的数值模拟研究展现了PDC钻头井底流场中存在的低速区、回流区和滞留区,为钻头的水力结构研究提供了一个新的研究思路和方向。G.MENSA-WILMOT等[4]于2002年指出,当喷嘴总射流面积一定时,更多数量的喷嘴可以提高携岩效果。以上PDC钻头流场数值模拟方法大多以单相流(井底钻井液流动)分析为主。A.MOSLEMI等[5]假设岩屑从井底射入流场,利用DPM(离散相)模型研究了井底流场中岩屑的运动情况,采用单向耦合方式将岩屑简化为球形样本颗粒插入井底流场来研究井底流场和携岩效果,只考虑了钻井液对岩屑颗粒的拖曳效果,并未考虑岩屑对流体的影响,且忽略了岩屑形状以及岩屑碰撞等力学行为。将CFD-DEM耦合应用于水平井PDC钻头井底流场的携岩研究较少。因此,本文采用CFD-DEM耦合方法,对水平井PDC钻头井底流场进行数值模拟,研究不同条件下井底流场岩屑运移情况,以期为后期水平井PDC钻头携岩问题研究提供参考。
1 水平井PDC钻头井底流场理论水平井PDC钻头的井底流场仍然遵循流体三大守恒定律:质量守恒、动量守恒和能量守恒。本文的研究主要针对钻井液对岩屑的运移作用,不考虑传热模型,因此主要考虑流体的质量守恒和动量守恒。采用可实现k-ε的湍流模型对旋转流场进行模拟研究。
用曳力、压力梯度力和旋转升力[6]来代表流体与颗粒的耦合作用力。
1.1 曳力曳力为流体与颗粒的相对运动而产生的扰流阻力,其表达式为:
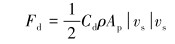
|
(1) |
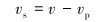
|
(2) |
式中:Fd为曳力,N;Cd为颗粒的曳力系数;ρ为流体密度,kg/m3;Ap为颗粒的投影面积,m2;vs为颗粒滑移速度,m/s;v为流体瞬时速度,m/s;vp为颗粒瞬时速度,m/s。
1.2 压力梯度力压力梯度力是指流体中颗粒的四周存在流体压力差而施加的力(包含浮力),它等于颗粒体积与压力梯度的乘积,计算公式如下:

|
(3) |
式中:Fp为压力梯度力,N;Vp为颗粒的体积,m3;▽pstatic为流体的静态压力梯度,Pa/m。
1.3 旋转升力旋转升力是颗粒旋转运动产生的与颗粒相对运动方向垂直的力,计算方程为:

|
(4) |
式中:FLR为旋转升力,N;Dp为颗粒直径,m;CLR为旋转升力系数;Ω为颗粒滑移角速度,rad/s。
对于PDC钻头井底携岩流场,钻头转动必然带动整个计算域旋转,那么颗粒会受到一个附加的体力,称为旋转流场附加体力[6]。其计算式为:
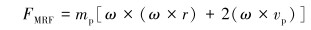
|
(5) |
式中:r为颗粒指向旋转轴线的距离矢量,m;mp为颗粒质量,kg;ω为颗粒的转动角速度, rad/s。
钻井中产生的岩屑之间会相互作用,故引入DEM控制方程,采用Hertz Mindlin无滑移接触模型[7]。考虑岩屑颗粒的滚动,使用滚动阻尼模型[8]。对应的方程如下。
Hertz Mindlin无滑移接触模型:
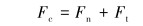
|
(6) |
式中:Fc为球体之间的接触合力,Fn为法向力,Ft为切向力,单位均为N。
对于法向接触力而言,可以简化为弹簧-阻尼力学模型,计算公式为:
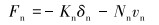
|
(7) |
式中:Kn为法向弹性恢复系数;δn为接触点处法向重叠量,N;Nn为法向阻尼力, N·s/m;vn为接触点处两个颗粒表面法向运动的相对速度,m/s。
对于切向接触力而言,可以简化为弹簧-阻尼-静摩擦力学模型,计算公式为:
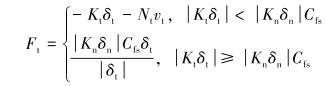
|
(8) |
式中:Kt为切向弹性恢复系数;δt为接触点处切向重叠量, N;Nt为切向阻尼力, N·s/m;vt为接触点处两个颗粒表面切向运动的相对速度,m/s;Cfs为静态摩擦因数。
滚动阻尼模型:
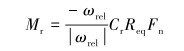
|
(9) |
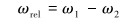
|
(10) |
式中:Mr为滚动阻尼力矩,N·m;ωrel为相对旋转角速度,rad/s;Cr为滚动摩擦因数;Req为两球体颗粒的等效半径,m;ω1、ω2为球体1、2的转动角速度,rad/s。
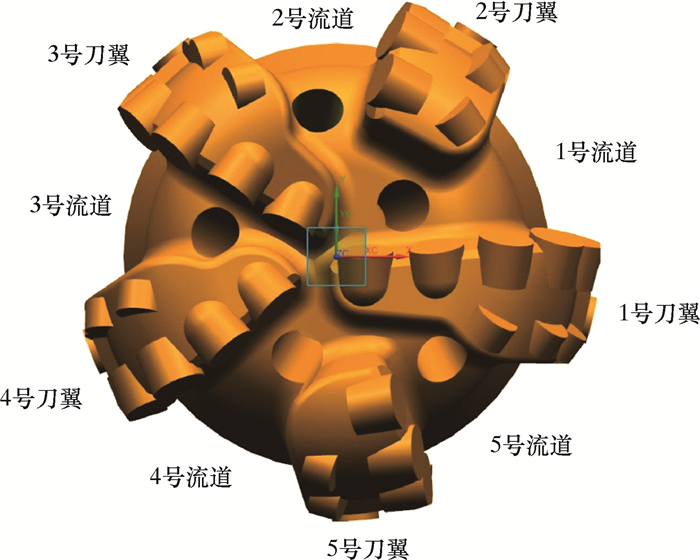
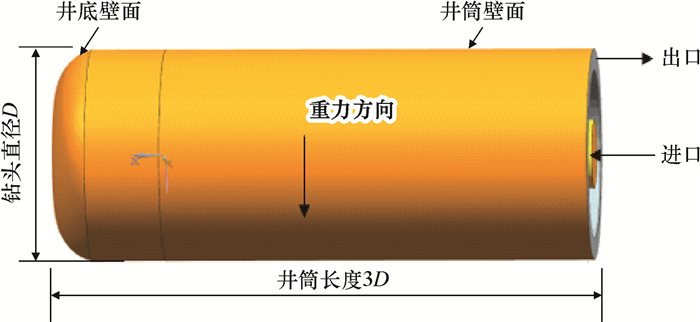
2 井底流场的数值模拟与结果分析 2.1 井底流场的建立以ø152.4 mm、五刀翼、五喷嘴并具有后排切削齿的PDC钻头为例,将PDC钻头的某些特征结构(如喷嘴出口)进行简化后,利用CAD软件建立钻头三维模型(见图 1)和钻头井底流场模型(见图 2)。利用多面体网格[9]处理技术对PDC钻头井底流场区域进行网格划分,如图 3所示。
|
| 图 1 水平井PDC钻头三维模型 Fig.1 Three-dimensional model of PDC bit in horizontal well |
|
| 图 2 水平井PDC钻头井底流场模型 Fig.2 Bottomhole flow field model of horizontal well with PDC bit |

|
| 图 3 水平井PDC钻头井底流场网格 Fig.3 Bottomhole flow field grid of horizontal well with PDC bit |
为了更加符合岩屑产生位置的实际情况,采用近齿面喷射。考虑水平井PDC钻头对岩屑有重复破碎作用和泥岩遇水变松软使岩屑颗粒细化,采用均值为3 mm的岩屑。每颗齿喷射岩屑的相关仿真数据(体积流量、初始速度大小和方向)利用UG的二次开发技术来获取[10]。岩屑密度2 500 kg/m3,弹性模量15 GPa,泊松比0.25。岩屑接触力学参数如表 1所示。钻井液密度2 000 kg/m3,动力黏度0.008 Pa·s,井底参考压力100 MPa(井深4 000 m+泵压20 MPa)。边界条件为:质量流进口、压力出口,钻头、钻杆壁面为运动无滑移边界,井底、井筒壁面为固定无滑移边界。
| 参数名称 | 岩屑与岩屑 | 岩屑与壁面 |
| 静摩擦因数 | 0.61 | 0.70 |
| 滚动摩擦因数 | 0.01 | 0.02 |
| 法向弹性恢复系数 | 0.50 | 0.50 |
| 切向弹性恢复系数 | 0.50 | 0.50 |
2.2 模拟结果分析
岩屑颗粒由PDC各齿面喷射进入流体计算域后,随钻井液流向出口,完成在井底流场中的运移过程。该过程的数值模拟计算由CFD-DEM双向耦合求解器主导完成。
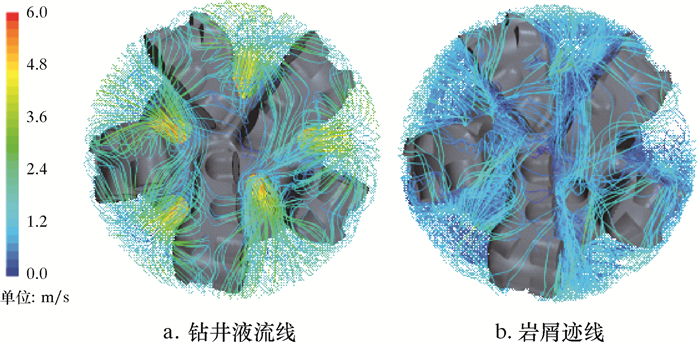
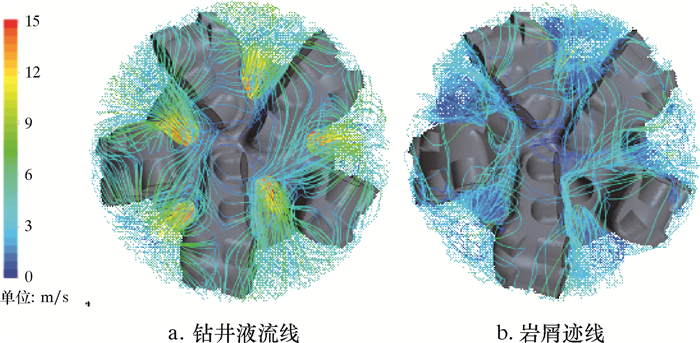
2.2.1 井底PDC钻头区域的岩屑运移分析不同钻井液排量下井底PDC钻头区域钻井液流线和岩屑运移轨迹如图 4~图 6所示。
|
| 图 4 钻井液排量为4 L/s时井底PDC钻头区域钻井液流线和岩屑轨迹 Fig.4 Drilling fluid flow line and cuttings trajectory around the PDC bit in the bottomhole under the displacement of 4 L/s |
|
| 图 5 钻井液排量为10 L/s时井底PDC钻头区域钻井液流线和岩屑轨迹 Fig.5 Drilling fluid flow line and cuttings trajectory around the PDC bit in the bottomhole under the displacement of 10 L/s |
|
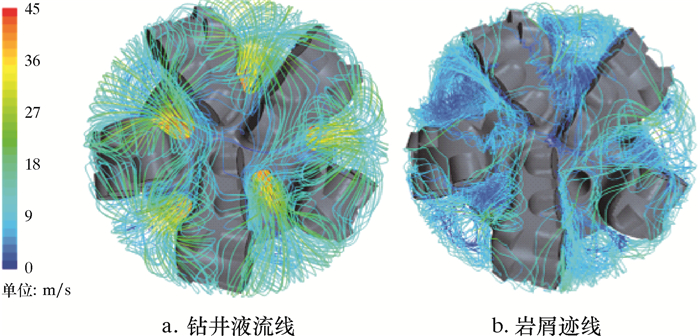
| 图 6 钻井液排量为30 L/s时井底PDC钻头区域钻井液流线和岩屑轨迹 Fig.6 Drilling fluid flow line and cuttings trajectory around the PDC bit in the bottomhole under the displacement of 30 L/s |
通过对比分析3种排量下的钻井液流线和岩屑轨迹可以发现,不论何种排量均会发生钻井液窜流现象。这说明钻井液在井底的流动情况与排量关系不大,主要与PDC钻头的水力结构有关。排量越低,岩屑在钻头心部区域的窜流越明显。在低排量情况下,由于钻井液与岩屑之间存在较小的相对运动速度,所以钻井液对井底初始岩屑的曳力作用较小,喷嘴射流作用随之减弱,岩屑的加速、转向变得比较困难。其中,从钻头各个刀翼主切削齿(距离钻头心部更近)产生的岩屑颗粒,如果没有获取足够的动能则很难实现转向和随井底漫流运移至出口,会在井底各个流道或刀翼之间发生岩屑的窜流现象。因此,排量越低,岩屑在钻头心部各刀翼之间的窜流现象越明显。若岩屑长时间滞留在井底,将会导致钻头心部的岩屑不断堆积,最终可能形成钻头中心泥包。
2.2.2 环空区域的岩屑运移分析(1) 重力对岩屑运移的影响。重力对水平井PDC钻头井底流场的影响主要体现在对钻井液和岩屑运动方向的改变。钻井液排量分别为4、10和30 L/s,钻头不旋转时1~3号流道后方环空区域中钻井液流线和岩屑运移轨迹如图 7~图 9所示。
|
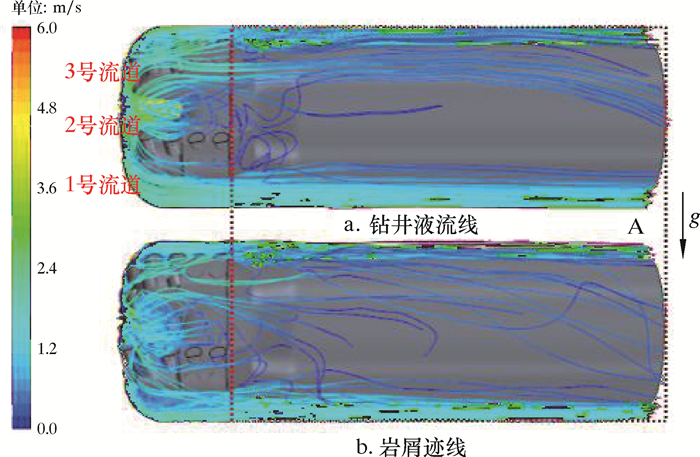
| 图 7 钻井液排量为4 L/s时环空区域钻井液流线和岩屑迹线 Fig.7 Drilling fluid flow line and cuttings trajectory in the annulus under the displacement of 4 L/s |
|
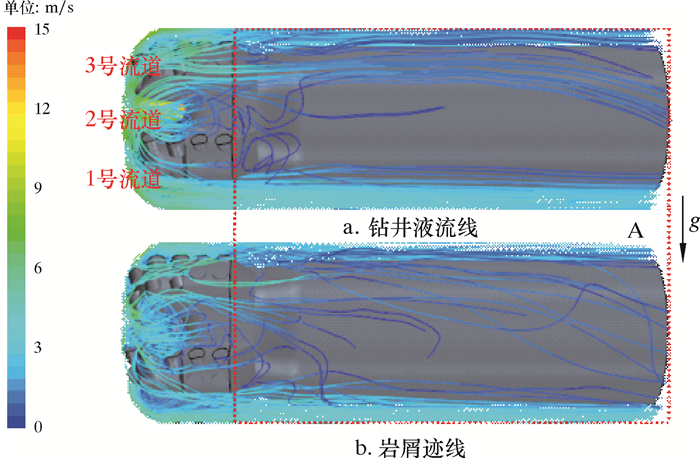
| 图 8 钻井液排量为10 L/s时环空区域钻井液流线和岩屑迹线 Fig.8 Drilling fluid flow line and cuttings trajectory in the annulus under the displacement of 10 L/s |
|
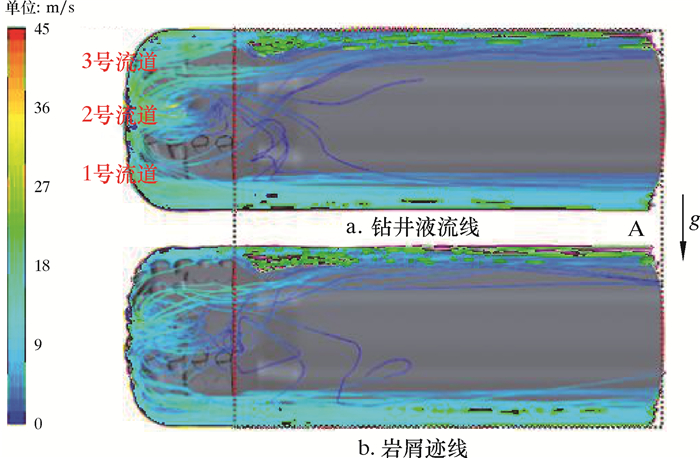
| 图 9 钻井液排量为30 L/s时环空区域钻井液流线和岩屑迹线 Fig.9 Drilling fluid flow line and cuttings trajectory in the annulus under the displacement of 30 L/s |
对比分析3种排量下的钻井液流线可以发现,钻井液排出到环空区域(A)后,2、3号流道的钻井液向1号流道偏移;排量越低钻井液轴向运动速度越小,重力作用越明显,钻井液的偏向行为越明显。因此,在水平井环空区域,特别是低排量的情况下,重力对于钻井液的作用不可忽略。
对于密度大于钻井液的岩屑而言,重力的作用将更加明显。对比钻井液流线和岩屑轨迹,岩屑在重力方向上的偏移程度比钻井液的偏移大很多,且排量越低,重力作用越明显。从图 7可见,排量为4 L/s的情况下,由于没有足够的运移动能,在重力的影响下,从2、3号流道靠近对应刀翼排出的岩屑在1号流道后方的环空区域出现了岩屑床。研究发现,岩屑床的堆积沿出口方向有逐渐增多的趋势,如图 10所示。
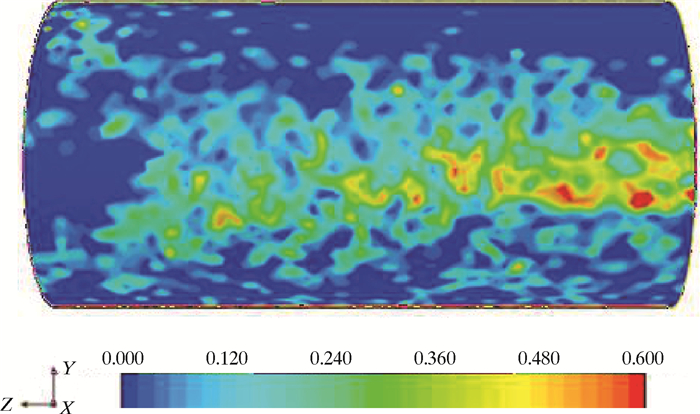
|
| 图 10 排量为4 L/s时井壁底部岩屑分布 Fig.10 Distribution of cuttings at the bottomhole under the displacement of 4 L/s |
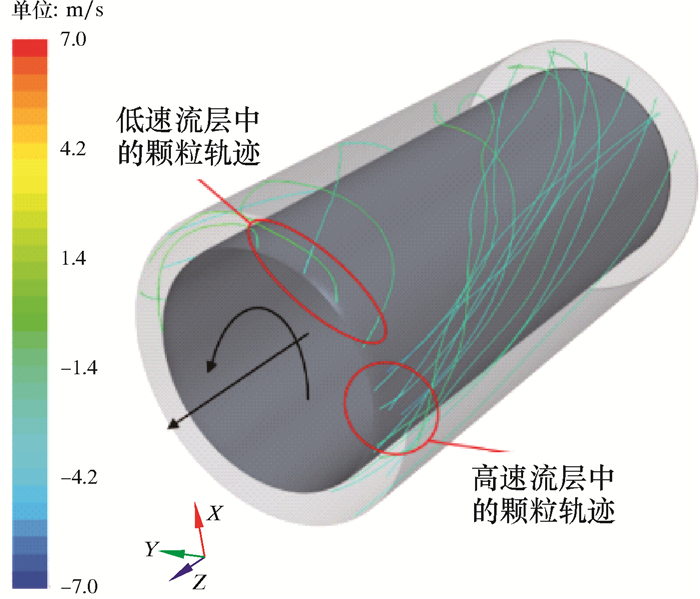
(2) 旋转对岩屑运移的影响。旋转作为环空区域中岩屑运移的重要因素,其主要作用是施加给岩屑一个旋转体力,改变岩屑的运动方向使其绕轴做旋转运动,呈现螺旋形的轨迹线。图 11为环空中部分颗粒的运动轨迹。
|
| 图 11 环空中部分颗粒的运动轨迹 Fig.11 Motion trajectory of some cutting particles in the annulus |
各流道排出钻井液的轴向速度存在分层,主流道对应高速流层,副流道对应低速流层。这会影响颗粒在环空中的运动轨迹线路,高速流层中的岩屑所受轴向曳力较大,可以减小旋转体力和重力的影响作用,有助于岩屑沿出口方向快速运移;低速流层中岩屑所受轴向曳力较小,旋转体力和重力影响作用明显,岩屑出现较大幅度转向。因此,在水平井环空区域,特别是在低排量的情况下,旋转对岩屑的运移作用也不可忽略。
3 携岩评价指标通常采用岩屑冲洗法来评价岩屑运移情况,但是这种试验方法是先放入岩屑,并不考虑岩屑不断生成的过程,这与实际钻井情况并不一致。因此,本文提出将岩屑滞留量和岩屑运移比作为水平井PDC钻头井底流场携岩效果的评价指标。
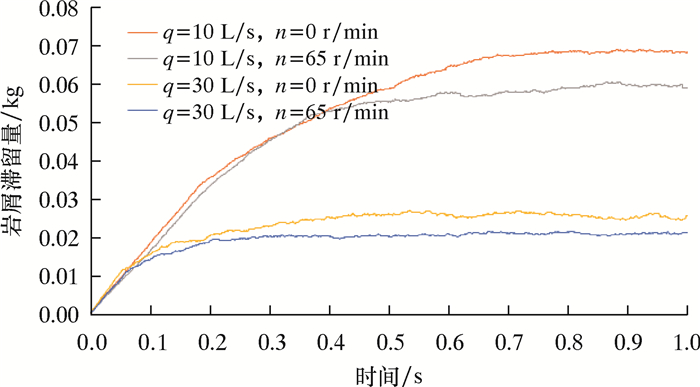
3.1 岩屑滞留量岩屑滞留量是指计算完成后整个流体域中剩余岩屑的总质量。图 12给出了不同排量以及钻头是否旋转工况下岩屑滞留量的变化曲线。图 12中q表示排量,n表示转速。
|
| 图 12 岩屑滞留量变化曲线 Fig.12 Cutting retention |
从图 12可以发现:高排量情况下,岩屑滞留量会以更快的时间达到稳定阶段,且稳定阶段的岩屑滞留量更少,说明高排量有助于井底岩屑的运移,这与实际钻井工程中采用高排量来提升井底清岩效果一致。分析认为旋转既可以使井底流场产生扰动来带动井壁下端滞留的岩屑向上端运动,也可以驱动岩屑做螺旋式运动,促进低速流层中的岩屑跃迁至高速流层,因此,旋转可以协助岩屑的运移,减少井底岩屑滞留量。这与文献[11]中钻柱旋转有利于水平井段中岩屑运移的结论一致。
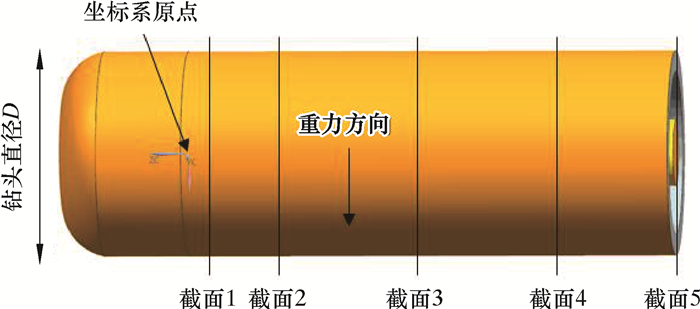
3.2 岩屑运移比岩屑运移比是指环空中不同截面上(环形截面)颗粒沿钻杆轴向的速度均值与该平面上钻井液轴向流速均值之比。选取5个截面来计算岩屑运移比,如图 13所示。图 13中截面1距最左边的距离等于钻头的直径,截面5在出口处,5个截面的中心距坐标原点的直线距离见表 2。
|
| 图 13 计算岩屑运移比的5个截面云图 Fig.13 Five sections for calculating the cutting migration ratio |
| 截面编号 | 1 | 2 | 3 | 4 | 5 |
| 距离/mm | 60 | 100 | 200 | 300 | 350 |
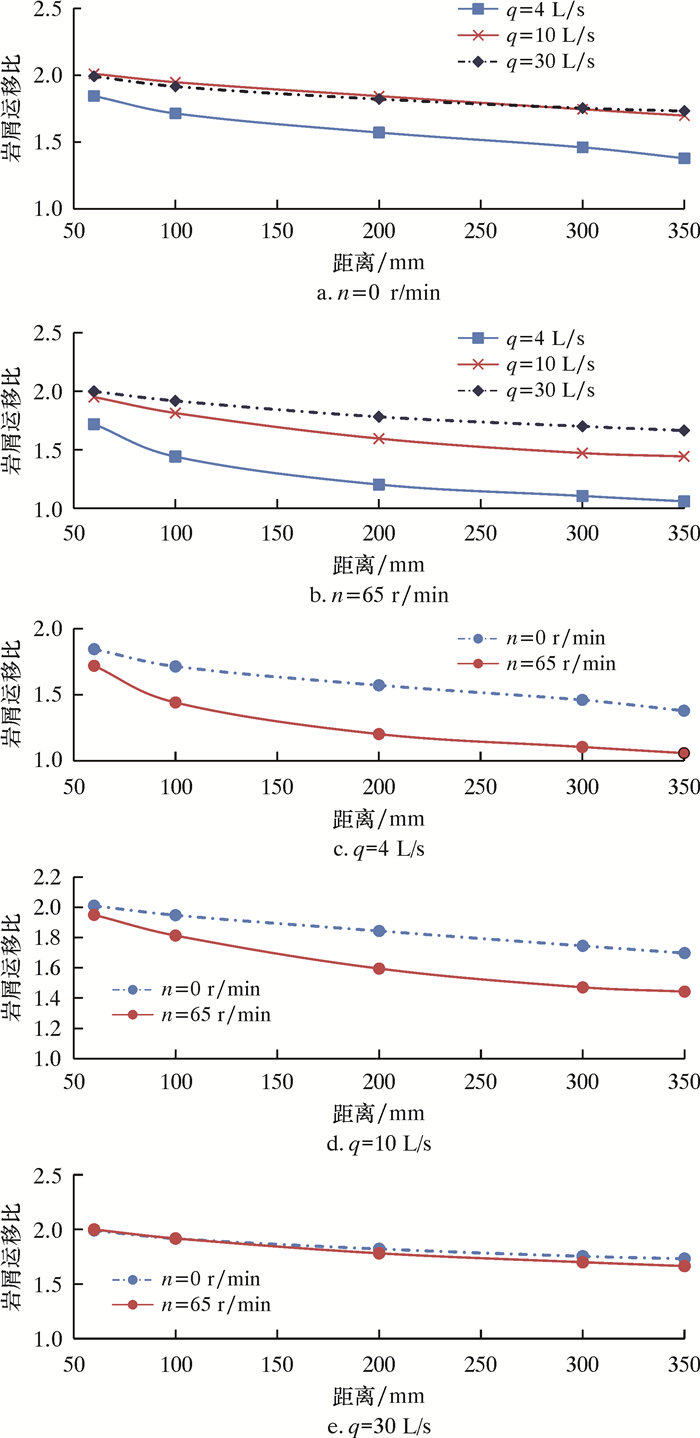
以前述水平井PDC钻头为例,在3种排量(4、10和30 L/s)和钻头是否旋转(0、65 r/min)情况下,给出了5个截面上的岩屑运移比,如图 14所示。观察各图发现:靠近井底的环空区域中岩屑的平均速度高于钻井液速度,岩屑运移比大于1;随着截面距离的增加,同一条件下的岩屑运移比呈现不断下降的状态,这是因为岩屑在井底环空中运移时,大部分岩屑(高速流层中)受到阻力使得动能不断被消耗,平均运移速度降低;钻头不旋转时,中高排量下的岩屑运移比相差不大,岩屑相对于钻井液而言有相同的运移状态,但低排量下的岩屑运移比就会小得多(见图 14a);钻头旋转时,3种排量下的岩屑运移比差异较大,排量越高,岩屑运移越好(见图 14b);相同排量下,钻头旋转会减小岩屑的运移比,因为与钻井液相比,拥有更大密度的岩屑将受到更大的旋转体力作用,使得轴向速度下降更快;排量越低,钻头旋转对岩屑运移比产生的影响将更大(见图 14c~图 14e)。
|
| 图 14 各工况下岩屑运移比 Fig.14 Cutting migration ratios under various working conditions |
4 结论
(1) 在井底PDC钻头区域,钻井液排量越小,岩屑在钻头心部区域的窜流越明显。钻井液的窜流与流量大小无关,主要与钻头水力结构有关。
(2) 在环空区域,钻井液排量越小,重力作用越明显,重力是井底出现岩屑床的主要因素。旋转体力可使岩屑从低速流层跃迁到高速流层,从而获取轴向运移动能,并随高速钻井液排向出口。
(3) 钻井液排量和旋转均会影响岩屑滞留量和岩屑运移比,可以用岩屑滞留量和岩屑运移比来评判井底旋转流场的携岩性能。
(4) 研究结果可为后续水平井PDC钻头携岩问题研究提供参考。
| [1] |
武治强, 周建良, 靳勇, 等. 页岩气水平井气层封固难点分析与技术对策[J]. 石油钻采工艺, 2012, 34(增刊1): 26-29. WU Z Q, ZHOU J L, JIN Y, et al. Difficulty analysis and technical countermeasures to the gas layer sealing ability for the shale gas horizontal well[J]. Oil Drilling and Production Technology, 2012, 34(S1): 26-29. |
| [2] |
CROUSE R, CHIA R. Optimization of PDC bit hydraulics by fluid simulation[R]. SPE 14221, 1985.
|
| [3] |
黄红梅, 翟应虎, 王辉, 等. 实体PDC钻头流场数值模拟与实验验证[J]. 中国石油大学学报(自然科学版), 2005, 29(3): 49-52. HUANG H M, ZHAI Y H, WANG H, et al. Numerical simulation and experimental checking for downhole flow field of a real PDC bit[J]. Journal of China University of Petroleum(Edition of Natural Science), 2005, 29(3): 49-52. DOI:10.3321/j.issn:1000-5870.2005.03.011 |
| [4] |
MENSA-WILMOT G, FEAR M. Innovative technology improves penetration rates of PDC bits in shales drilled at great depth with weighted water based mud systems[C]//IADC/SPE Drilling Conference, Dallas, Texas: [s.n.], 2002.
|
| [5] |
MOSLEMI A, AHMADI G. Study of the hydraulic performance of drill bits using a computational particle-tracking method[J]. SPE Drilling & Completion, 2014, 29(1): 28-35. |
| [6] |
Siemens PLM Software Inc. STAR-CCM+:user guide, version 12.02[M]. Plano, TX USA: Siemens PLM Software Inc., 2017.
|
| [7] |
ALBERTO DI RENZO, FRANCESCO DI MAIO. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes[J]. Chemical Engineering Science, 2004, 59: 525-541. DOI:10.1016/j.ces.2003.09.037 |
| [8] |
KUANG S B, YU A B, ZOU Z S. Computational study of flow regimes in vertical pneumatic conveying[J]. Ind. Eng. Chem. Res, 2009, 48(14): 6846-6858. DOI:10.1021/ie900230s |
| [9] |
许晓平, 周洲. 多面体网格在CFD中的应用[J]. 飞行力学, 2009, 27(6): 87-89. XU X P, ZHOU Z. Application of polyhedral mesh in CFD[J]. Flight Dynamics, 2009, 27(6): 87-89. |
| [10] |
况雨春, 陈玉中, 屠俊文, 等. 基于UG/OPEN的PDC钻头切削参数仿真方法[J]. 石油钻探技术, 2014(4): 111-115. KUANG Y C, CHEN Y Z, TU J W, et al. Simulation of cutting parameters of PDC bit based on UG/OPEN[J]. Petroleum Drilling Techniques, 2014(4): 111-115. |
| [11] |
李志刚.基于钻柱旋转的水平井段岩屑运移实验研究[D].大庆: 东北石油大学, 2016. LI Z G. Study on experiment of horizontal well drill cuttings migration based on the rotation of the section[D].Daqing: Northeast Petroleum University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10220-1016221001.htm |



