2. 常州大学石油工程学院
2. School of Petroleum Engineering, Changzhou University
0 引言
2017年,中国石油表观消费量增速回升,石油表观消费量约为5.88亿t,增速为5.9%[1]。管道运输目前已成为油气运输的首要方式。截至2017年底, 中国境内在役油气管道总里程累计约13.31万km[2]。
埋地管道是城市的重要基础设施之一。管道失效造成的挥发性有机物泄漏一方面会引起灾难性的环境污染,另一方面会造成经济损失和人员伤亡,对国民经济构成严重威胁[3-6]。埋地管道泄漏常发生在地面以下,因此准确预测管道泄漏的污染范围和泄漏量可以为后期制定应急抢险方案提供理论支撑,也是建立科学高效的应急管理平台的关键。
近年来,随着CFD(计算流体力学)技术的发展,采用数值计算方法对污染物渗流扩散问题进行数值模拟的研究越来越多,J.C.PARKER等[7]利用参数模型得到了油品在非饱和区的相对渗透率和毛细压力的关系,并且通过试验证明了其适用性。郑德凤等[8]在国外多相流渗流试验的基础上进行了LNAPL的迁移扩散规律研究。武晓峰等[9]利用多孔介质毛细管模型,推导求得了毛细压力折算系数。付建民等[10]通过液相管道小孔泄漏试验系统,构建不同试验场景,研究了输送中流量、压力对管内流体压力及泄漏速率的影响规律,提出了小孔管道泄漏稳定压力的计算方法。李朝阳、李泽和马贵阳等[11-14]借助CFD软件对土壤中油品的渗流扩散进行模拟,研究了弯头、含水率和泄漏孔位置等对泄漏扩散的影响。张伟等[15]对液氨储罐泄漏后的扩散危险性进行FLUENT数值模拟研究,对比分析了不同条件下液氨储罐泄漏后的扩散情况和危害。杜明俊等[16]通过FLUENT软件数值模拟了埋地输油管道泄漏口在不同位置时泄漏前后大地温度场的变化。史晓蒙等[17]建立了地面油品泄漏的计算流体力学仿真模型,得到了油品扩展速度关于泄漏流量的关系式。符泽第等[18]通过CFD软件模拟了河流穿越管道泄漏后柴油泄漏扩散情况,分析了泄漏孔径、泄漏速度和水流速度对泄漏扩散的影响。目前针对输送压力对原油泄漏扩散范围的相关研究报道还不多见。
本文通过建立埋地长输管道稳态泄漏扩散过程的物理模型和数学模型,模拟不同输送压力下原油在土壤中的稳态泄漏扩散过程,进而分析了原油泄漏后的污染物扩散范围和泄漏量等参数的变化规律。
1 泄漏扩散模型 1.1 物理模型在建立模型时做以下基本假设:①假定土壤气相为理想气体且不含有水蒸气;②原油为单一组分,是不可压缩且不具备挥发性的流体;③土壤为连续的多孔介质,具有各向同性;④仅考虑油品在土壤非饱和区的渗流扩散;⑤在土壤中的流动均为层流,且满足达西定律;⑥不考虑溶质吸附、分解和其他化学作用。
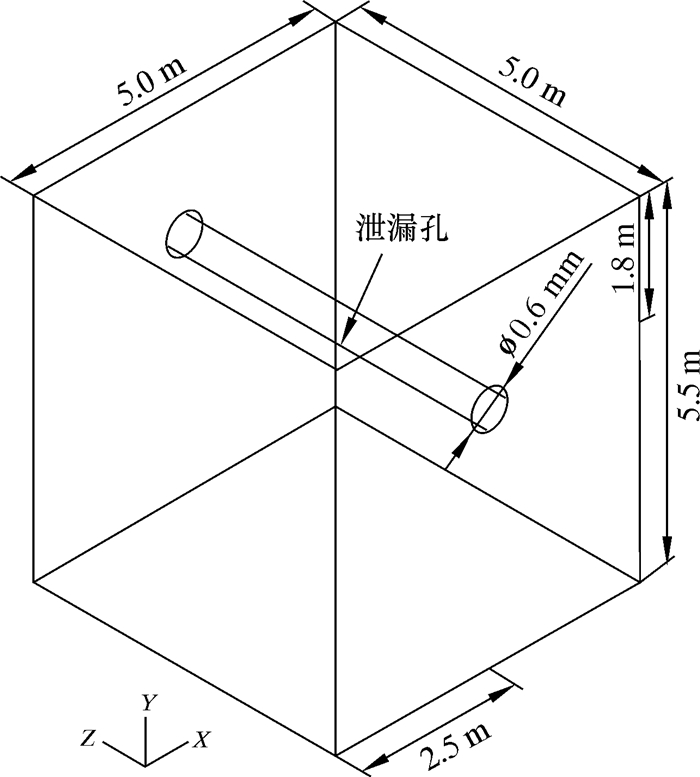
利用ICEM建立了管道及周围土壤区域的三维几何模型。管道埋深1.8 m,管道外径606 mm,壁厚3 mm,输送介质为原油,管道的下部存在一个0.06 m×0.04 m的长方形泄漏口。对该模型采用结构化网格划分,并对泄漏口附近的土壤和管道进行了加密处理。经过网格无关性验证,最终选择的计算模型总网格数达到101万,最低网格质量为0.75,且95%的网格质量高于0.90,满足计算精度要求。埋地管道泄漏的物理模型及管道周围土壤网格模型分别如图 1和图 2所示。
|
| 图 1 埋地管道泄漏三维物理模型 Fig.1 Three-dimensional physical model of buried pipeline with leakage |

|
| 图 2 埋地管道泄漏网格模型 Fig.2 Grid model of the buried pipeline with leakage |
1.2 数学模型
泄漏油品在土壤中的扩散过程是一个复杂的多相流驱替过程,本文的研究思路建立在宏观平均的流体和理想化的多孔介质模型基础上,同时涉及油、气、水三相,采用了VOF模型。
连续性方程:
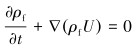
|
(1) |
式中:U为流体速度,m/s;ρf为流体密度,kg/m3;t为时间,s。
体积分数连续性方程:
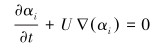
|
(2) |
式中:αi为第i相的体积分数。
其余的特性参数均是通过几种流体的组合表示,以密度为例可以表示为式(3),其他特性参数,如黏度等都按照此方法算得。
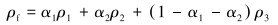
|
(3) |
式中:α1、α2为第1相和第2相的体积分数;ρ1、ρ2、ρ3分别为第1~3相的密度,kg/m3。
动量守恒方程为:
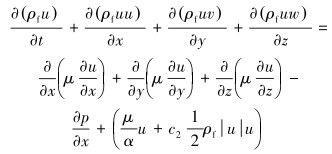
|
(4) |
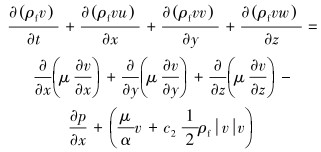
|
(5) |
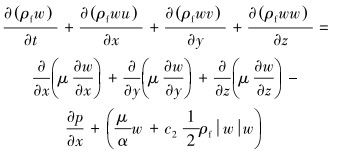
|
(6) |
式中:u、v、w分别为U在x、y、z方向上的速度分量,m/s;α=Dp2ε3/ [150 (1-ε) 2]为多孔介质的渗透率,m2;c2=3.5 (1-ε )/ (Dpε3)为惯性损失系数,m-1;ε为多孔介质的孔隙比;p为多孔介质的孔隙压力,Pa;Dp为多孔介质的粒子直径,mm;μ为流体的动力黏度,Pa·s。
能量守恒方程为:
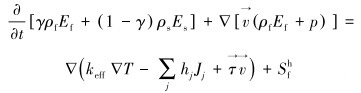
|
(7) |
式中:Ef为流体的总能,J;Es为多孔介质的总能,J;ρs为多孔介质的密度,kg/m3;T为多孔介质的温度,K;hj是组分j的焓;Jj是组分j的扩散通量,kg/(m·s);γ为多孔介质的孔隙度;Sfh为流体的焓源项,J/kg;keff为多孔介质的有效导热率,W/(m·K);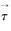
用有限体积法对上述数学模型进行离散,为了使方程封闭有解,引入标准k-ε模型。由于土壤中的泄漏扩散涉及油、气、水三相,本文在研究中采用了VOF多相流模型。采用pressure-based求解器和适合瞬态计算的PISO算法进行求解,松弛因子为0.5。
边界条件如下:管道入口采用压力入口条件,压力值分别设为4、8和12 MPa,管道出口采用速度入口条件;土壤四周及上边界采用压力出口条件,下边界考虑到是饱和水层采用壁面条件;泄漏口采用interior边界条件。
2 数值模拟及结果分析原油密度为870 kg/m3,黏度为3×10-3 Pa·s。管道周围土壤平均粒径为0.5 mm,孔隙体积分数为0.45,土壤密度为2 650 kg/m3,含水体积分数为0.2。管道输送压力分别为4、8和12 MPa,管道内原油的流速为1.8 m/s。
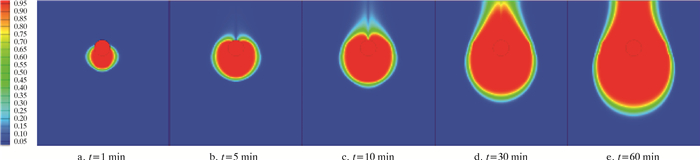
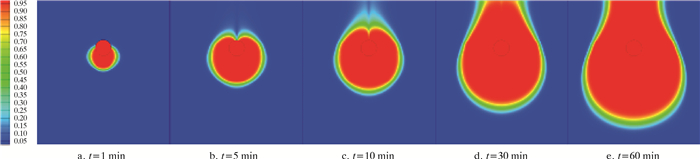
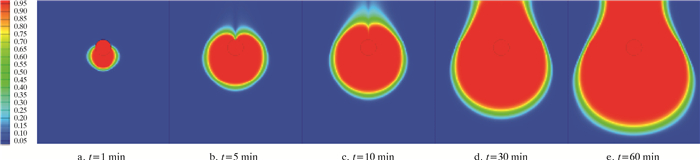
2.1 油相分布云图管道压力分别为4、8和12 MPa时,泄漏后的原油扩散分布情况如图 3~图 5所示。不同压力条件下土壤中的原油体积分布可以划分为三个区域,分别是完全扩散区(原油体积分数为1)、过渡区(原油体积分数介于0到1之间)和未扩散区(原油体积分数为0)。从图 3~图 5可以看出:完全扩散区的面积随着泄漏时间延长也逐渐增大;在泄漏初期,由于管道泄漏口向下同时受重力影响,完全扩散区集中在管道下部的土壤区域,完全扩散区呈现苹果状;随着泄漏的不断发展,下部积聚的原油不断增加,由于毛细阻力增大和土壤下层的压力大于表层土壤,向下的扩散速度放缓,原油克服自身重力开始向上扩散,完全扩散区呈现灯泡状,过渡区的体积也在不断增大;之后,原油不断向上扩散直至地表,随着泄漏时间的推移在地表的扩散面积不断增大;同时扩散过程也在向下和四周进行,最终呈现出花瓶状。对于不同压力下的埋地原油管道泄漏,原油的体积分布有着明显的区别,主要体现在泄漏相同时间时,完全扩散区的面积随着埋地管道压力的增大而增大,典型形状的停留时间随着埋地管道压力的增大而缩短。
|
| 图 3 管道压力为4 MPa时不同时刻土壤中的径向原油分布 Fig.3 Radial crude oil distribution in soil at different times under the pipeline pressure of 4 MPa |
|
| 图 4 管道压力为8 MPa时不同时刻土壤中的径向原油分布 Fig.4 Radial crude oil distribution in soil at different times under the pipeline pressure of 8 MPa |
|
| 图 5 管道压力为12 MPa时不同时刻土壤中的径向原油分布 Fig.5 Radial crude oil distribution in soil at different times under the pipeline pressure of 12 MPa |
2.2 扩散速度场分析
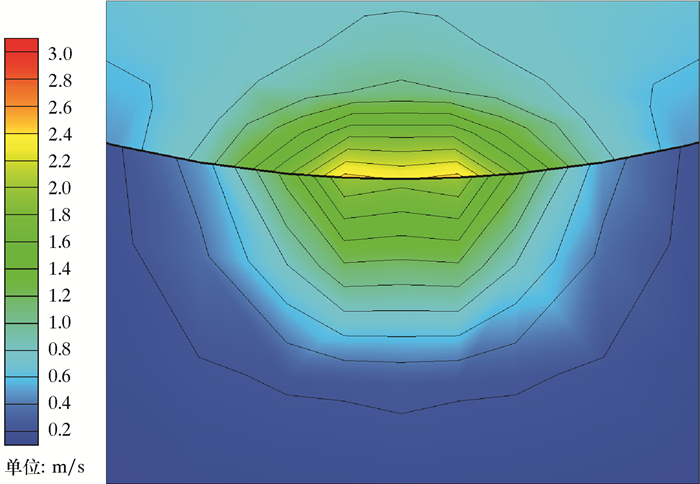
将泄漏口附近土壤和管道放大约30倍,可以清晰看见不同输送压力下原油在土壤中的泄漏速度等值线图,如图 6~图 8所示。
|
| 图 6 管道压力为4 MPa时土壤中的速度等值线图 Fig.6 Velocity contour map of soil under the pipeline pressure of 4 MPa |
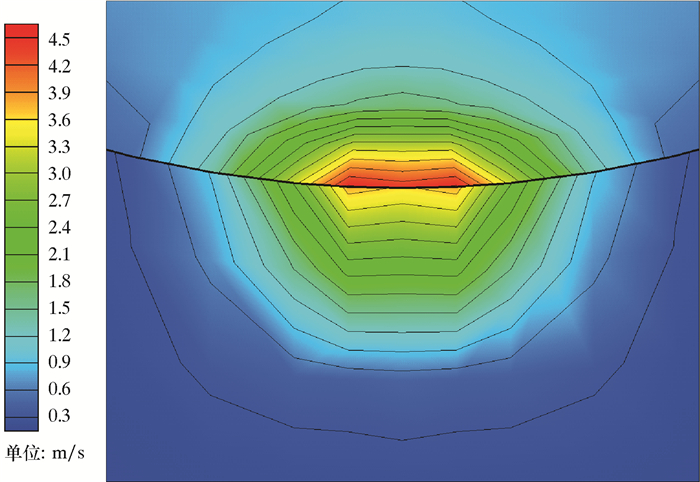
|
| 图 7 管道压力为8 MPa时土壤中的速度等值线图 Fig.7 Velocity contour map of soil under the pipeline pressure of 8 MPa |
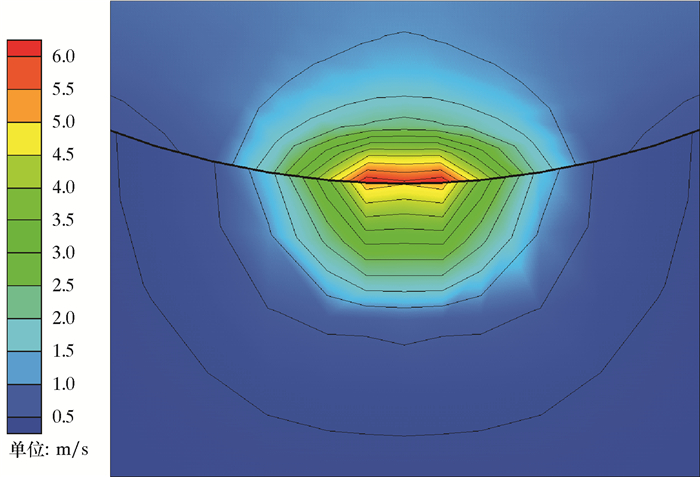
|
| 图 8 管道压力为12 MPa时土壤中的速度等值线图 Fig.8 Velocity contour map of soil under the pipeline pressure of 12 MPa |
从图 6~图 8可以看出:泄漏口附近的管道和土壤中的流速最大,向四周辐射状减小;泄漏口的管道侧流速略大于土壤侧,因为在土壤侧受到了土壤的毛细力和驱替空气和水时的阻力作用;外围区域流速非常低,符合达西渗流和层流的前期假设。压力对泄漏后的速度场影响体现在泄漏口附近的最大流速随压力的增大而增大,输送压力为4 MPa的管道泄漏口速度为3.07 m/s;当输送压力增加到8 MPa,泄漏口速度增加至原先的147%;当输送压力增加到12 MPa时,泄漏口速度增加至原先的207%。初始压力的增大使泄漏口两侧的压力差增大,在高度变化忽略不计的情况下,流速显著增大。同时管道输送压力分别为4、8和12 MPa时,流速从最大的泄漏口位置到最小的边缘位置的距离分别为0.067、0.076和0.070 m。对于输送压力较大的管道泄漏,其泄漏速度向四周减小的速率大于输送压力较小的管道,因为在土壤中所受的阻力随流动速度增大而增大,而且初期泄漏速度大导致积聚的原油较多,从而增大了驱替水和空气时所受的阻力。
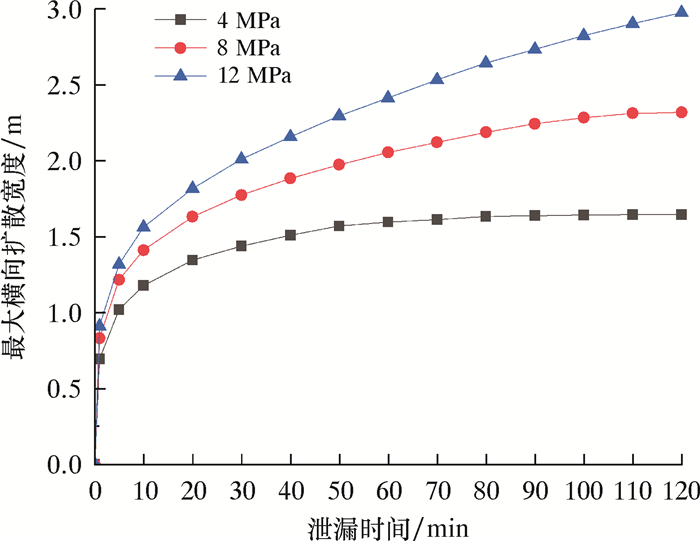
2.3 横向和纵向扩散分析不同输送压力下原油在土壤中泄漏的最大扩散距离变化过程如图 9和图 10所示。
|
| 图 9 不同压力的管道泄漏后最大横向扩散宽度对比 Fig.9 Comparison of maximum lateral diffusion width |
|
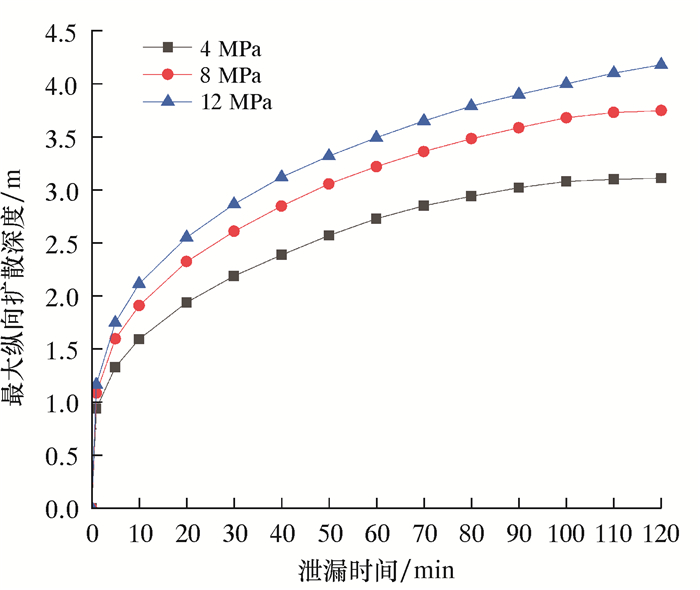
| 图 10 不同压力的管道泄漏后最大纵向扩散深度对比 Fig.10 Comparison of maximum longitudinal diffusion depth after pipe leakage under different pressures |
从图 9和图 10中可以看出:原油的横向和纵向扩散与时间呈非线性关系,初期扩散速率明显较大,随后逐步减小,最后趋于平稳。其原因在于随着泄漏的不断进行,土壤中的原油不断积聚导致驱替周围水和空气的阻力不断增大。同时由于受自重的影响,在扩散到土壤中的水饱和区前,纵向扩散的能力强于横向扩散,纵向扩散深度平均是横向扩散宽度的144%。对于不同压力下的管道泄漏,横向和纵向的扩散速度都随着管道压力的增大而增大,但是可以发现随着压力的增大,横向和纵向扩散的增速放缓,管道输送压力从4 MPa提升至8 MPa,扩散距离平均提升了22%,管道输送压力从8 MPa提升至12 MPa,扩散距离平均提升了12%,原因是压力的增大引起泄漏速率增大,从而导致了扩散所受到的阻力增大。同时随着压力的增大,扩散范围曲线趋近于平稳所需的时间也在增加。管道输送压力为4 MPa时,70 min时扩散范围曲线就趋于平稳,当管道输送压力提升到8 MPa时,时间延长至110 min。
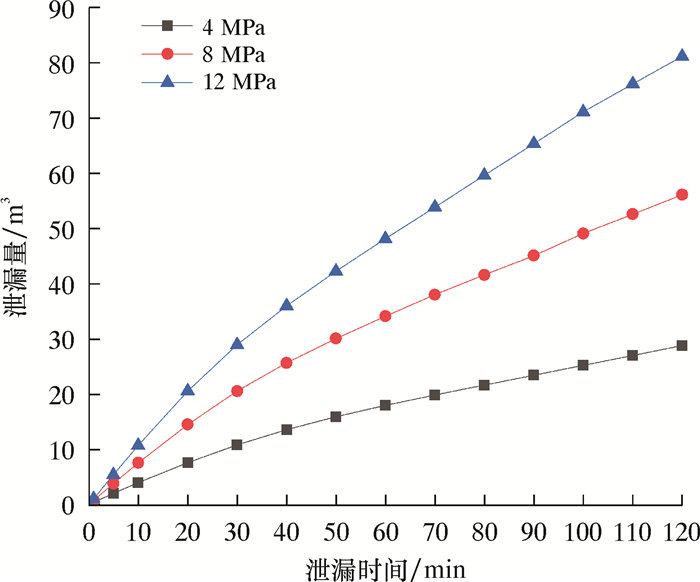
2.4 泄漏量分析不同输送压力下原油在土壤中的泄漏量变化过程如图 11所示。
|
| 图 11 不同输送压力下的管道泄漏量变化过程 Fig.11 Comparison of pipeline leakage under different transportation pressures |
从图 11可以看出:泄漏量的增长速率随时间缓慢减小,原因在于管道稳态泄漏时在其余条件不变的情况下流量不变,但是随着泄漏的不断发展,积聚的原油使所受的阻力增大,所以泄漏速率缓慢减小;对于不同压力下的管道泄漏,随着管道压力的增大,泄漏量也增大,输送压力12 MPa的管道泄漏量是4 MPa的2.07倍,输送压力8 MPa的管道泄漏量是4 MPa的1.47倍。原因在于初始管道压力的增大,使得泄漏稳定时的压力变大,从而使得泄漏速率增大,所以在泄漏口面积不变的情况下,泄漏量也增大。
3 结论(1) 三种压力条件下,原油在土壤中的运移趋势相同,可分为三个区域,其中完全扩散区在泄漏初期为苹果状,逐步发展为灯泡状,最后呈现花瓶状。
(2) 在非饱和区埋地管道的稳态泄漏扩散范围和泄漏时间保持一定的规律。泄漏初期扩散范围增速较大,之后逐步减小,最后趋于平稳。管道的输送压力越大,相同时间下的泄漏扩散距离越大,但是扩散距离的增速随着压力的增大逐渐放缓。管道输送压力从4 MPa提升至8 MPa和12 MPa,扩散距离平均提升22%和38%。同时随着管道输送压力的增大,扩散范围曲线趋近于平稳所需的时间也在延长。
(3) 管道发生泄漏后,泄漏口的速度最大,向四周辐射状减小,边缘区域流速非常低。随着输送压力的增大,泄漏口的流速增大,同时流速随距离向四周减小的速率增大,输送压力8 MPa的管道泄漏口速度是输送压力4 MPa的147%,输送压力12 MPa的管道泄漏口速度是输送压力4 MPa的207%。
| [1] |
佚名.《2017年国内外油气行业发展报告》发布: 中国原油对外依存度67.4%[J].上海化工, 2018, 43(2): 5. ANON. 2017 domestic and foreign oil and gas industry development report released: China's crude oil dependence on foreign countries 67.4%[J]. Shanghai Chemical Industry, 2018, 43(2): 5. |
| [2] |
高鹏, 高振宇, 杜东. 2017年中国油气管道行业发展及展望[J]. 国际石油经济, 2018, 26(3): 21-27. GAO P, GAO Z Y, DU D. Development and prospects of China's oil and gas pipeline industry in 2017[J]. International Petroleum Economics, 2018, 26(3): 21-27. DOI:10.3969/j.issn.1004-7298.2018.03.003 |
| [3] |
朱庆杰, 赵晨, 陈艳华, 等. 埋地天然气管道泄漏的影响因素及保护措施[J]. 环境工程学报, 2018, 12(2): 417-420. ZHU Q J, ZHAO C, CHEN Y H, et al. Influencing factors and protective measures of buried natural gas pipeline leakage[J]. Chinese Journal of Environmental Engineering, 2018, 12(2): 417-420. |
| [4] |
慕园, 余志峰, 刘玉卿. 埋地管道通过逆断层的有限元分析[J]. 石油机械, 2015, 43(10): 112-115. MU Y, YU Z F, LIU Y Q. Strength analysis of buried gas pipeline in reverse fault[J]. China Machinery Petroleum, 2015, 43(10): 112-115. |
| [5] |
夏梦莹, 张宏, 王宝栋, 等. 基于壳单元的连续型采空区埋地管道应变分析[J]. 油气储运, 2018, 37(3): 256-262. XIA M Y, ZHANG H, WANG B D, et al. Strain analysis of buried pipelines in continuous mining subsidence areas based on shell element[J]. Oil & Gas Storage and Transportation, 2018, 37(3): 256-262. |
| [6] |
刘洪飞, 韩阳, 冯新, 等. 埋地管道微小泄漏与保温层破坏分布式光纤监测试验[J]. 油气储运, 2018, 37(10): 1114-1120. LIU H F, HAN Y, FENG X, et al. Test on tiny leakage and insulating layer damage monitoring of buried oil pipelines using distributed optical fiber temperature sensor[J]. Oil & Gas Storage and Transportation, 2018, 37(10): 1114-1120. |
| [7] |
PARKER J C, LENHARD R J, KUPPUSAMY T. A parametric model for constitutive properties governing multiphase flow in porous media[J]. Water Resources Research, 1987, 23(4): 618-624. DOI:10.1029/WR023i004p00618 |
| [8] |
郑德凤, 赵勇胜, 王本德. 轻非水相液体在地下环境中的运移特征与模拟预测研究[J]. 水科学进展, 2002(3): 321-325. ZHENG D F, ZHAO Y S, WANG B D. Migration characteristics and simulation prediction of LNAPL in underground environment[J]. Advances in Water Science, 2002(3): 321-325. DOI:10.3321/j.issn:1001-6791.2002.03.010 |
| [9] |
武晓峰, 唐杰, 藤间幸久. 多孔介质两相流的统一毛细压力——饱和度关系曲线[J]. 灌溉排水, 2000(2): 15-18. WU X F, TANG J, TENGJIANU X J. Niform capillary pressure-saturation curve of two-phase flow in porous media[J]. Journal of Irrigation and Drainage, 2000(2): 15-18. DOI:10.3969/j.issn.1672-3317.2000.02.003 |
| [10] |
付建民, 赵振洋, 陈国明, 等. 液相管道流量与压力对小孔泄漏速率的影响[J]. 石油学报, 2016, 37(2): 257-265. FU J M, ZHAO Z Y, CHEN G M, et al. Influences of liquid pipeline flow and pressure on small-hole leakage rate[J]. Acta Petrolei Sinica, 2016, 37(2): 257-265. |
| [11] |
李朝阳, 马贵阳, 刘亮. 埋地输油管道泄漏油品扩散模拟[J]. 油气储运, 2011, 30(9): 674-676. LI C Y, MA G Y, LIU L. Simulation of oil spill diffusion in buried oil pipeline[J]. Oil & Gas Storage and Transportation, 2011, 30(9): 674-676. |
| [12] |
李泽, 马贵阳, 常方圆. 埋地管道在不同含水率的土壤中泄漏数值模拟[J]. 当代化工, 2014, 43(11): 2460-2463. LI Z, MA G Y, CHANG F Y. Numerical simulation of leakage of buried pipelines in soils with different moisture contents[J]. Contemporary Chemical Industry, 2014, 43(11): 2460-2463. DOI:10.3969/j.issn.1671-0460.2014.11.079 |
| [13] |
李朝阳, 马贵阳, 刘亮. 输油管道弯头穿孔泄漏数值模拟[J]. 中国安全科学学报, 2010, 20(9): 56-59. LI C Y, MA G Y, LIU L. Numerical simulation of hole perforation leakage in oil pipeline[J]. China Safety Science Journal, 2010, 20(9): 56-59. DOI:10.3969/j.issn.1003-3033.2010.09.010 |
| [14] |
李朝阳, 马贵阳, 刘亮. 输油弯管泄漏数值模拟[J]. 当代化工, 2011, 40(4): 420-422. LI C Y, MA G Y, LIU L. Numerical simulation of oil pipeline leakage[J]. Contemporary Chemical Industry, 2011, 40(4): 420-422. DOI:10.3969/j.issn.1671-0460.2011.04.028 |
| [15] |
张伟, 雷云, 王海东, 等. 基于Fluent数值模拟的液氨储罐泄漏扩散危险性研究[J]. 环境工程, 2015, 33(增刊1): 718-721, 736. ZHANG W, LEI Y, WANG H D, et al. Study on diffusion risk of liquid ammonia tank leak based on fluent numerical simulation[J]. Environmental Engineering, 2015, 33(S1): 718-721, 736. |
| [16] |
杜明俊, 马贵阳, 高雪利, 等. 埋地输油管道泄漏影响区内大地温度场的数值模拟[J]. 石油规划设计, 2010, 21(5): 24-26. DU M J, MA G Y, GAO X L, et al. Numerical simulation of earth temperature field in the zone of impact of buried oil pipeline leakage[J]. Petroleum Planning & Engineering, 2010, 21(5): 24-26. DOI:10.3969/j.issn.1004-2970.2010.05.007 |
| [17] |
史晓蒙, 吕宇玲, 杨玉婷, 等. 地面输油管道泄漏流散数值模拟[J]. 中国安全生产科学技术, 2017, 13(1): 90-96. SHI X M, LÜ Y L, YANG Y T, et al. Numerical simulation on spread after leakage of ground oil pipeling[J]. Journal of Safety Science and Technology, 2017, 13(1): 90-96. |
| [18] |
符泽第, 兰惠清, 张永龙, 等. 河流穿越管道小孔泄漏数值模拟[J]. 油气储运, 2014, 33(1): 10-14. FU Z D, LAN H Q, ZHANG Y L, et al. Numerical simulation on small hole leakage of river crossing pipeline[J]. Oil & Gas Storage and Transportation, 2014, 33(1): 10-14. |


