0 引言
连续管水力喷射环空加砂多级压裂是目前油气藏储层改造和试油完井作业的一项重要技术,广泛应用于低渗透油气藏及页岩气藏储层改造中,最大程度地实现了储层的精细化改造,提高了油气井的压裂增产效果。为了进一步提高连续管水力压裂的改造效果,有效降低连续管环空最高压裂作业压力,笔者前期提出了一种新的水力波动注入压裂增产工艺,即通过人为地快速改变压裂泵组工作转速(或工作频率),实现压裂泵组不稳定的排量和压力输出,这种不稳定的注入方式可以实现裂缝的有效扩展和提高压裂的增产效果[1]。作为水力压裂的关键部件,连续管在井下的力学行为和性能好坏直接关系着油气井压裂施工的成败。在水力波动注入压裂作业中,连续管承受复杂的动态载荷,如动态的外压、轴向力以及弯曲接触力等耦合载荷。在复杂的动态载荷作用下,连续管的载荷模式、应力状态和结构完整性可能会呈现出不同的力学规律,同时,复杂的动态载荷容易引起连续管强度降低、变形失效和疲劳断裂等问题,直接影响水力波动注入压裂增产工艺的成功应用和连续管的动力强度安全性。
目前,国内外学者针对连续管的研究主要集中在极限强度、失效机理、失稳屈曲、变形、疲劳寿命、模拟试验以及水力摩阻等方面[2-15],并取得了大量的认识和结论,但是上述研究均在稳定流体注入方式下进行,涉及波动注入水力压裂作业中连续管的动态力学行为研究很少。为此,笔者根据流体力学、材料力学及弹性力学理论,分析了水力波动注入压裂(即不稳定外界激励)下连续管的动态力学行为,以期通过合理控制压裂泵组排量与工作转速、优选连续管尺寸与钢级等参数,确保水力波动注入压裂作业中连续管动力强度处于一定的安全范围内。该研究对揭示水力波动注入压裂作业中连续管的失效机理和实施水力波动注入压裂增产工艺具有重要的理论价值和现实意义。
1 连续管载荷模型 1.1 环空动态压力水力波动注入环空压裂过程中,井筒内注入流体的波动压力为[16]:

|
(1) |
式中:p(x, t)为环空任意深度和流动时间下流体的波动压力,MPa;ρo为环空内流体密度,g/cm3;
为便于分析环空动态压力,假设井筒轴线与连续管轴线重合,即不考虑井筒中连续管环空偏心对环空流速和摩阻的影响。水力波动注入压裂作业中,连续管环空任意时间、任意井深处的压力po(x, t)为:

|
(2) |
式中:pow为环空不稳定井口压力,MPa;ρo为环空流体密度,g/cm3,g为重力加速度,m/s2;pof为环空注入流体的摩阻,MPa。
环空注入流体的摩阻为:

|
(3) |
式中:fao为环空流体摩阻系数,由环空流体流态决定;u(x, t)为环空流体波动流速,m/s。
环空中压裂液是典型的非牛顿流体,其流变特性变化较大。从流变学角度而言,非牛顿压裂液的流变模式主要为幂律流型和宾汉流型两种,理论上认为非牛顿流体幂律流型更接近实际压裂液。因此,环空中压裂液流变模式为幂律流型时,环空流体雷诺数Reao为[17-18]:

|
(4) |
式中:na为环空流性指数,无量纲;Ka为环空稠度系数,Pa·sn。
非牛顿流体在连续管环空内的摩阻系数为[19]:

|
(5) |
联立式(3)~式(5)可得环空注入流体的摩阻,再将计算的摩阻和文献[16]波动流速代入式(2),即可得到水力波动注入压裂作业中连续管的环空动态压力。
1.2 内压力水力波动注入压裂过程中,需要以恒定的排量在连续管内注入一定的平衡压力,则连续管的内压力pi(x)为:

|
(6) |
式中:piw为连续管内井口压力,MPa;ρi为连续管内流体密度,g/cm3;pif为连续管内注入流体的摩阻,MPa。
连续管内注入流体的摩阻为:

|
(7) |
其中

|
(8) |
式中:vit为连续管内流体流速,m/s;Qi为连续管内流体注入排量,m3/min;dt为连续管内径,m;fit为连续管内流体摩阻系数,由连续管内注入流体流态决定。
实际压裂作业中,连续管内注入流体认为是非牛顿流体,仍然按照非牛顿流体幂律流型进行计算。当连续管内注入流体流变模式为幂律流型时,连续管内流体雷诺数为[17-18]:

|
(9) |
式中:nt为连续管内流性指数;Kt为连续管内稠度系数,Pa·sn。
非牛顿流体在连续管内的摩阻系数为[13]:

|
(10) |
式中:a和b为计算系数。
当Reit<3 470-1 370nt时,认为管内流体处于层流,此时a=16,b=1;当Reit>4 270-1 370nt时,认为管内流体处于紊流,此时系数a和b由管内流性指数nt决定,即有:

|
(11) |
联立式(7)~式(11)可得连续管内注入流体的摩阻,再将计算的摩阻代入式(6),即可得连续管内任意井深处的压力。
需要说明的是,由于连续管本身直径小,管内流体流动空间小,实际作业中连续管内流体的流态一般为紊流,所以按照紊流计算连续管内注入流体的摩阻。
1.3 轴向力水力波动注入压裂过程中,井筒中连续管所受的轴向力主要包括:井口注入头施加的轴向力、连续管重力、内外流体压力产生的轴向力及连续管弯曲后与套管内壁接触产生的摩擦力。显然,水力波动注入压裂作业中,任意时间下任意深度处(朝井深增加的方向)连续管轴向力的变化率为:

|
(12) |
式中: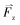
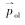
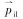
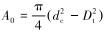
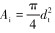
式(12)在任意深度x处积分得:

|
(13) |
式中:Fz(x, t)为作用于任意井深x处连续管末端的输出挤压力,kN;输入力Fin(0)为井口注入头施加的挤压力,kN。
式(13)描述了水力波动注入压裂作业中井口注入头输入的挤压力与连续管末端输出的挤压力之间的关系。在井斜角θ较小时,连续管沿轴向方向上的分力较大,其输出轴向力为变量。若位于封隔器l处,则Fz(l, t)可视为连续管施加在封隔器上的动态轴向力。计算时采用式(13)判断垂直井中连续管是否发生屈曲,进而确定是否有接触力,即可获得垂直井中连续管的实际输出挤压力。
1.4 接触力与弯矩若连续管末端输出的挤压力Fz(x, t)超过连续管的临界屈曲载荷,井眼中连续管将发生屈曲并与套管壁接触,则会产生一定的接触力和弯矩。根据文献[5-6],水力波动注入压裂作业中屈曲连续管与套管壁间的接触力和弯矩为:

|
(14) |

|
(15) |
式中:N(x, t)为连续管与井壁套管之间的动态接触力,kN;M(x, t)为屈曲连续管产生的动态弯矩,kN·m;δr为连续管与井眼套管之间的径向间隙,m;E为连续管钢材弹性模量,MPa;I为连续管横截面惯性矩,m4,且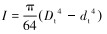
将式(13)代入式(14)和式(15),即可得到连续管与套管壁接触的动态接触力和弯矩计算模型。
2 连续管应力与强度失效判据根据上述分析,水力波动注入压裂作业中,连续管在环空压力po(x, t)、内压pi(x)、轴向力Fz(x, t)、弯矩M(x, t)与接触力N(x, t)联合作用下,处于三向复杂应力状态下工作。
2.1 径向应力与环向应力在环空压力po(x, t)和内压pi(x)作用下,连续管的径向应力和环向应力为[20]:

|
(16) |

|
(17) |
式中:σr为连续管径向应力,MPa;σθ为连续管环向应力,MPa。
2.2 轴向应力轴向力Fz(x, t)作用下连续管的轴向应力(拉为正,压为负)为:

|
(18) |
式中:σaz为连续管轴向应力,MPa。
弯矩M(x, t)作用下连续管的弯曲应力(拉为正,压为负)为:

|
(21) |
式中:σm为连续管弯曲应力,MPa;Iz为连续管横截面惯性矩,m4,且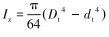
连续管弯曲凸起的一侧受附加弯曲拉应力,凹进的一侧受附加弯曲压应力。在弯矩作用下,连续管内壁和外壁截面产生的附加弯曲应力不同,实际计算时以连续管的内壁和外壁分别进行两次计算,即计算连续管内外壁4个点上的弯曲应力,然后与轴向应力叠加形成总的轴向应力。
连续管总的轴向应力为:

|
(20) |
式中:σz为连续管总的轴向应力,MPa。
2.3 剪切应力接触力N(x, t)(相当于横向剪力)作用下连续管的剪切应力为:

|
(21) |
式中:τ为连续管剪切应力,MPa。
2.4 等效应力与安全系数根据第四强度理论,在径向应力、环向应力、轴向应力和剪切应力作用下,连续管的等效应力为[19]:

|
(22) |
式中:σxd4为连续管等效应力,MPa。
在上述复杂应力状态下,连续管的工作安全系数为:

|
(23) |
式中:ns为连续管工作安全系数。
2.5 强度失效判据Von Mises屈服准则认为等效应力σxd4达到连续管管材的屈服强度σs时,连续管将发生屈服破坏。在三向复杂应力状态下,井下连续管发生屈服的失效判据为:

|
(24) |
式(24)表明连续管屈服状态为4个应力状态和屈服强度的函数。当f(σz, σr, σθ, σs, τ) < 0时,连续管的应力状态为弹性状态;f(σz, σr, σθ, σs, τ)=0时,连续管本体内任一点应力状态为屈服状态。
上述载荷、应力和强度失效判据模型可以真实地反映水力波动注入压裂过程中井下连续管的载荷分布、应力状态和动力强度情况。具体分析时,应首先根据输出轴向力与井下连续管的临界屈曲载荷的对比结果,判断连续管是否发生了屈曲,确定其接触力N(x, t),然后利用上述连续管应力计算公式计算相应的应力,最后再根据强度失效判据评估水力波动注入压裂过程中连续管的动力强度安全性。
3 参数敏感性分析某直井井深3 641 m,最大井斜角10.5°,采用∅139.7 mm×9.17 mm P110套管完井。该井拟采用∅50.8 mm×3.962 mm(2 in×0.156 in)QT900连续管带底封隔器拖动水力喷射多级压裂工艺对盒8下1、山12气层进行压裂改造,射孔层位约3 450和3 500 m。已知水力波动注入压裂阶段,连续管内注入排量Qi=0.2 m3/min,井口压力piw=20 MPa,管内流体密度ρi=1.02 g/cm3,管内流性指数nt=0.45,管内稠度系数Kt=0.8 Pa·sn;环空主压裂泵数为1,柱塞数为5,曲轴转速600~2 400 r/min,运转相位φ=π/3,瞬态输出排量Q ~ =3.0~5.0 m3/min,环空瞬态输出井口压力p ~=60 MPa,环空流体密度ρo=1.25 g/cm3,环空流性指数na=0.34,环空稠度系数Ka=6.2 Pa·sn;井口注入头施加轴向压力10 kN;连续管单位长度质量mq=4.58 kg/m,油管钢材泊松比μ=0.3,弹性模量E=2.06×105 MPa,屈服强度σs=620 MPa;连续管与套管摩擦因数μf=0.3。下面分析水力波动注入压裂作业中该井连续管的环空动态压力及动力强度安全性。
3.1 环空动态压力分析连续管环空动态压力随井深和流动时间的变化曲线分别如图 1和图 2所示。由图 1可以看出:水力波动注入压裂作业中,相同井深处连续管环空动态压力随流动时间的增加呈波动形式的变化,且变化幅度范围为每100 m增加5.00~8.00 MPa;相同流动时间下,随着井深的增加,连续管环空动态压力增大,且最大增加幅度范围为0.86~1.39 MPa。这表明井深和注入时间对连续管环空动态压力有一定的影响。由图 2可以看出,与稳定排量注入方式相比,在降低井口环空压裂作业压力的前提下,采用波动注入方式仍然可以增加连续管环空动态压力。这表明在确保井底环空压裂压力的前提下,采用波动注入方式对降低连续管井口环空最高压裂作业压力具有一定的积极作用。

|
| 图 1 连续管环空动态压力随井深和流动时间的变化曲线 Fig.1 Change of CT annulus dynamic pressure with flow time under different depths |

|
| 图 2 稳定与波动注入下连续管环空动态压力随井深的变化曲线 Fig.2 Change of CT annulus dynamic pressure with well depths under stable and wave injections |
在井深3 500 m处及其他已知条件下,计算得到连续管环空动态压力随压裂泵工作转速和排量的变化曲线,如图 3所示。由图 3可以看出,水力波动注入压裂作业中,压裂泵的工作转速存在一个最佳的工作转速范围,即1 000 ~2 000 r/min。在该最佳工作转速范围内,可通过快速改变压裂泵工作转速的方式来产生不稳定的注入排量,从而增加连续管环空动态压力。由此可见,压裂泵的工作转速和排量对连续管环空动态压力有明显影响。实际波动注入压裂作业中,建议使变频压裂泵组在最佳工作转速范围内工作,这样可以适当降低环空压裂排量和井口环空最高压裂作业压力。

|
| 图 3 连续管环空动态压力随压裂泵工作转速和排量的变化曲线 Fig.3 Change of CT annulus dynamic pressure with rotation speed and flow rate of fracturing pump |
3.2 动力强度安全性分析
根据分析,在危险截面处连续管内壁为应力危险点,因此由式(22)和式(23)进行计算,得出在环空动态压力、内压、轴向力、接触力与弯矩联合作用下,连续管内壁的等效应力与安全系数随井深和流动时间的变化曲线,如图 4和图 5所示。由图 4可以看出:相同井深处连续管等效应力随流动时间呈动态变化;当井深超过2 500 m、注入时间在1 400~1 900 s时,连续管的等效应力变化幅度较大,最大变化幅度小于20 MPa;相同注入时间下,随着井深的增加,连续管的等效应力增大,井深每增加100 m,连续管的平均等效应力约增加2.4 MPa。全井段连续管的最大等效应力为417.27 MPa,由失效判据式(24)可知,由于连续管钢材QT900屈服强度为620 MPa,全井段连续管不会发生屈服破坏。由图 5可以看出,连续管的安全系数与等效应力变化趋势刚好相反,全井段连续管最大等效应力417.27 MPa所对应的最小安全系数为1.49,能够满足气井压裂改造动态工况下管柱安全系数的要求。

|
| 图 4 连续管等效应力随井深和流动时间的变化曲线 Fig.4 Change of equivalent stress of CT with flow time under different depths |

|
| 图 5 连续管安全系数随井深和流动时间的变化曲线 Fig.5 Change of safety factor of CT with flow time under different depths |
上述分析结果表明,该井应用水力波动注入压裂工艺,虽然在一定程度上影响了井下连续管的动力强度,但是可以确保全井段连续管处于安全状态。因此建议实际压裂作业中,采用水力波动注入压裂工艺进行油气藏储层改造作业。
4 结论及建议(1) 综合考虑压裂泵波动排量与压力、工作转速、流体摩阻等因素,建立了水力波动注入压裂作业中连续管环空动态压力模型,该模型可真实反映波动注入对连续管环空压力的影响。
(2) 与稳定排量注入方式相比,采用波动注入方式可以降低连续管井口环空最高压裂作业压力。
(3) 水力波动注入压裂作业中,变频压裂泵组的最佳工作转速范围为1 000~2 000 r/min,在该范围内,可通过快速改变压裂泵工作转速的方式来产生不稳定的注入排量,从而增加井底需要的波动压裂压力。
(4) 水力波动注入压裂工艺对井下连续管的动力强度虽有一定影响,但仍可确保压裂作业中全井段连续管处于安全状态。建议实际压裂作业中,采用水力波动注入压裂工艺进行油气藏储层改造作业。
| [1] |
仝少凯, 高德利. 水力压力波动注入压裂增产工艺的力学原理[J]. 石油钻采工艺, 2018, 40(2): 265-274. TONG S K, GAO D L. Mechanical principles of hydraulic pressure fluctuation injection based on fracturing technology[J]. Oil Drilling & Production Technology, 2018, 40(2): 265-274. |
| [2] |
何东升, 武学尧, 雷建安. 连续管的工作能力计算[J]. 西安石油学院学报(自然科学版), 2002, 17(2): 37-40. HE D S, WU X Y, LEI J A. Computation of the operation ability of coiled tubing[J]. Journal of Xi'an Petroleum Institute (Natural Science Edition), 2002, 17(2): 37-40. DOI:10.3969/j.issn.1673-064X.2002.02.010 |
| [3] |
LIU J B, HE C S, YUE Q B. The mechanical analysis of the coiled tubing[J]. Applied Mechanics and Materials, 2013, 385. |
| [4] |
LIU S H, XIAO H, GUAN F, et al. Coiled tubing failure analysis and ultimate bearing capacity under multi-group load[J]. Engineering Failure Analysis, 2017, 79: 803-811. DOI:10.1016/j.engfailanal.2017.05.007 |
| [5] |
MITCHELL R F. New concepts for helical buckling[J]. SPE 15470-PA, 1988. |
| [6] |
MITCHELL R F. Exact analytic solutions for pipe bucking in vertical and horizontal wells[R]. SPE 72079-PA, 2002.
|
| [7] |
QIN X, GAO D L. The effect of residual bending on coiled tubing buckling behavior in a horizontal well[J]. Journal of Natural Gas Science and Engineering, 2016, 30: 182-194. DOI:10.1016/j.jngse.2016.02.016 |
| [8] |
TIPTON S M. Coiled-tubing deformation mechanics diametral growth and elongation[R]. SPE 36336, 1998.
|
| [9] |
LI L, SHEN Z X, WANG P. Research on the coiled tubing deformation under internal pressure and cyclic bending[J]. Applied Mechanics and Materials, 2013, 421: 62-65. DOI:10.4028/www.scientific.net/AMM.421 |
| [10] |
JI Y F, ZHANG H, DUAN Q Q, et al. Research on the analysis of coiled tubing fatigue life[J]. Applied Mechanics and Materials, 2011, 66: 1173-1178. |
| [11] |
ZHANG L G, YUE Q B, LUO M. The prediction of the low cycle fatigue life about the coiled tubing withovality and wall thickness[J]. Journal of Failure Analysis and Prevention, 2017, 17(12): 1288-1296. |
| [12] |
管锋, 段梦兰, 马卫国, 等. 连续管井下力学行为模拟实验研究[J]. 力学与实践, 2012, 34(5): 21-27. GUAN F, DUAN M L, MA W G, et al. The experimental simulation of mechanical behavior of coiled tubing in wells[J]. Mechanics in Engineering, 2012, 34(5): 21-27. |
| [13] |
GALLEGO F, SHAH S N. Friction pressure correlations for turbulent flow of drag reducing polymer solutions in straight and coiled tubing[J]. Journal of Petroleum Science and Engineering, 2009, 65(3/4): 147-161. |
| [14] |
信石玉, 宋代诗雨. 涪陵深层页岩气开发装备配套方案与建议[J]. 钻采工艺, 2017, 40(1): 108-111. XIN S Y, SONG D S Y. Supporting plan and suggestion for deep shale gas development equipment in Fuling[J]. Drilling & Production Technology, 2017, 40(1): 108-111. DOI:10.3969/J.ISSN.1006-768X.2017.01.31 |
| [15] |
明瑞卿, 贺会群, 唐纯静, 等. 国内外连续管软件研究分析[J]. 石油钻采工艺, 2017, 39(6): 771-780. MING R Q, HE H Q, TANG C J, et al. Study and analysis on domestic and foreign software related with coiled tubing[J]. Oil Drilling & Production Technology, 2017, 39(6): 771-780. |
| [16] |
仝少凯, 高德利. 不稳定流体注入时裂缝内压力和尖端应力分析[J]. 石油机械, 2018, 46(11): 65-71. TONG S K, GAO D L. Analysis of pressure and tip stress in hydraulic fracture under unstable fluid injection[J]. China Petroleum Machinery, 2018, 46(11): 65-71. |
| [17] |
WILLINGHAM J D, SHAH S N. Friction pressures of Newtonian and non-Newtonian fluids in straight and reeled coiled tubing[R]. SPE 60719, 2000.
|
| [18] |
JAWORSKY A S, REED T D. Predicting friction pressure losses in coiled tubing operations[J]. World Oil, 1997, 218(9): 141-146. |
| [19] |
MA D J, LI G S, HUANG Z W, et al. A model of calculating the circulating pressure loss in coiled tubing ultra-short radius radial drilling[J]. Petroleum Exploration and Development, 2012, 39(4): 528-533. DOI:10.1016/S1876-3804(12)60072-X |
| [20] |
徐芝纶. 弹性力学(上册)[M]. 北京: 高等教育出版社, 2006: 100-103. XU Z L. Elastic mechanics[M]. Beijing: Higher Education Press, 2006: 100-103. |
| [21] |
刘鸿文. 材料力学(Ⅱ)[M]. 北京: 高等教育出版社, 2004: 147-158. LIU H W. Mechanics of materials(Ⅱ)[M]. Beijing: Higher Education Press, 2004: 147-158. |


