2. 中国石油大学(华东)机电工程学院
2. College of Mechanical and Electronic Engineering, China University of Petroleum(Huadong
0 引言
示功图是煤层气井生产管理与评价的重要参数,由抽水机的悬点示功图可以求出煤层气井动液面,从而实现对煤层气井稳定降液控制,间接实现煤层气的精细排采。
目前,煤层气井的地面示功图一般通过示功图传感器实测获得。该传感器不仅价格高,而且存在零点漂移、测量精度变化的问题,需人工定期进行停产标定,费时费力,不能满足煤层气井连续、实时监测需要,影响煤层气井生产分析的及时性。相关文献[1-5]提出通过测定驱动电机的输入电参数,间接得到示功图的方法,包括功率转化法和功率损耗转化法,可以解决测量不连续的问题。但功率转化法没有考虑惯性和系统效率,功率损耗转化法难以建立统一的功率损耗模型,存在较大误差,其精度不能满足现场需要。
针对上述问题,本文基于抽水机实际模型,建立了电参数与载荷间的输入输出系统模型,提出了一种基于优化算法、利用电参数反演计算示功图的方法。该方法可根据实时采集的功率参数,实现动液面的自动实时监测。本文的研究旨在实现煤层气井生产分析的智能化,有利于煤层气井实时优化运行和增效。
1 电示功图求解动液面分析受煤层气井套管环空内死油环等因素的影响,目前的动液面测试仪器测试分析结果与实际液面不符,且不能实现连续、实时测试[6]。而电参数可以实现连续测量,使用电参数进行动液面检测是实现动液面连续检测的有效方法。由于示功图形状及悬点载荷对动液面影响明显,所以可以根据示功图数据确定相对准确的动液面数据,并将其应用于实际生产。
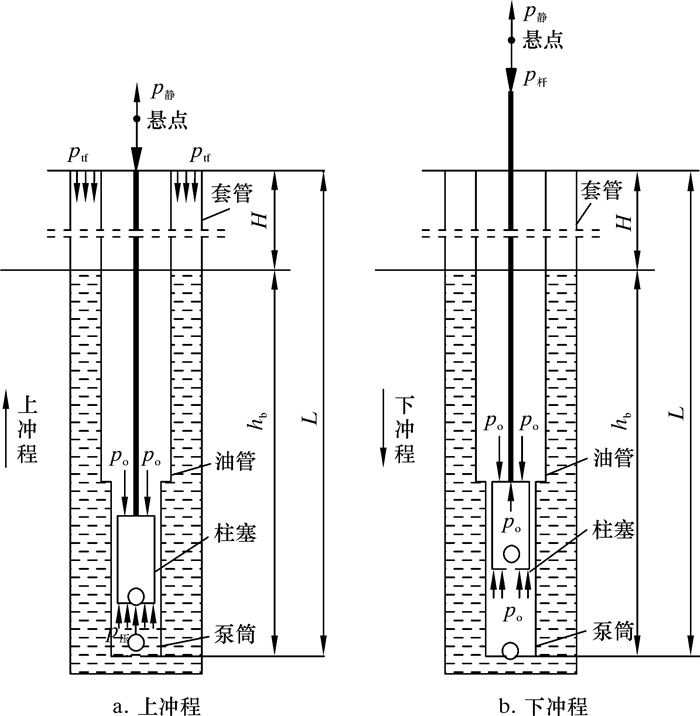
根据抽水机工作过程中阀开闭前、后泵腔内压力及泵载的变化规律[7],对井下悬点载荷进行受力分析,计算时简化动力示功图,无需考虑弹性振动载荷。抽水机上、下冲程受力分析如图 1所示。图中,hb为泵的沉没度,ptf为套压作用力,po为油液作用在柱塞上的力。
|
| 图 1 抽水机上、下冲程受力分析 Fig.1 Force analysis of the water pumping system during the up stroke and down stroke |
上冲程中,悬点从下死点上移,游动阀关,固定阀开,此时悬点承受抽油杆重力、油液重力、柱塞上方水的压力、管套环空的沉没度压力和管柱内摩擦力,则有:
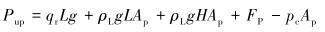
|
(1) |
式中:qr为每米抽油杆在液体中的质量,kg/m;L为泵深,m;ρL为油管内流体密度,kg/m3;H为动液面深度,m;Ap为柱塞面积,m2;Fp为柱塞与泵筒摩擦力[8],N;pc为套管压力,MPa。
其中:

|
(2) |
式中:D为柱塞直径,m;e为柱塞与衬套的间隙,m。
下冲程中,悬点从上死点下移,游动阀开,固定阀关。悬点承受杆柱在油中重力和管柱内摩擦力,则有:
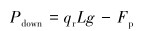
|
(3) |
综合式(1)和式(3)可得动液面计算公式:
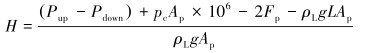
|
(4) |
建立基于示功图的动液面计算模型,由示功图的载荷差求出动液面。
2 电参数求解示功图通过建立考虑系统惯性和效率的系统动力学方程,计算功率,并将其与实测电机功率对比,应用Powell优化算法求解示功图。
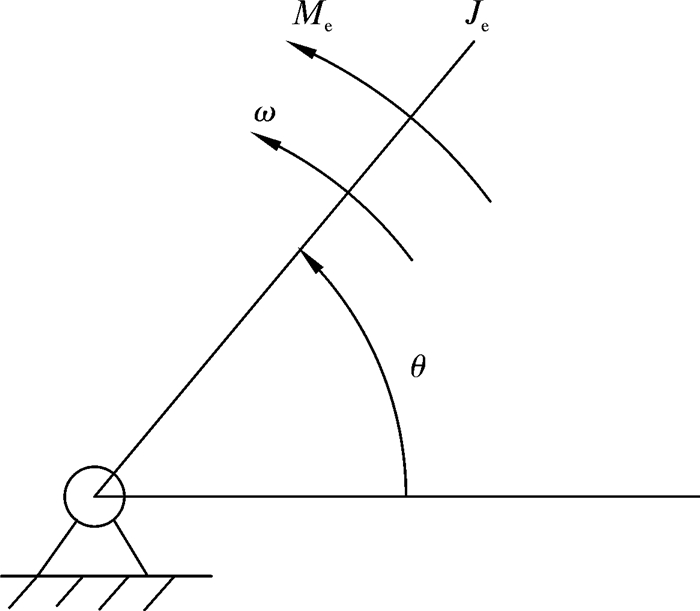
2.1 等效动力学模型的建立为了求解抽水机的实际运动规律,建立抽水机动力分析的等效动力学模型。取曲柄为等效构件,如图 2所示。
|
| 图 2 抽水机系统等效构件 Fig.2 Equivalent link of the water pumping system |
根据系统动能定理可得系统等效动力学方程:

|
(5) |
式中:Je为抽水机系统等效到曲柄轴的转动惯量,kg·m2;ω为等效构件曲柄角速度,rad/s;Me为抽水机系统等效到曲柄的等效力矩,N·m;θ为等效构件曲柄转角,rad。
其中:
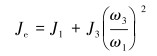
|
(6) |
式中:J1为曲柄、减速器和电动机等效到曲柄上的转动惯量,kg·m2;J3为游梁系统绕游梁回转中心的转动惯量,kg·m2;ω3为游梁角速度,rad/s;ω1为曲柄角速度,rad/s。
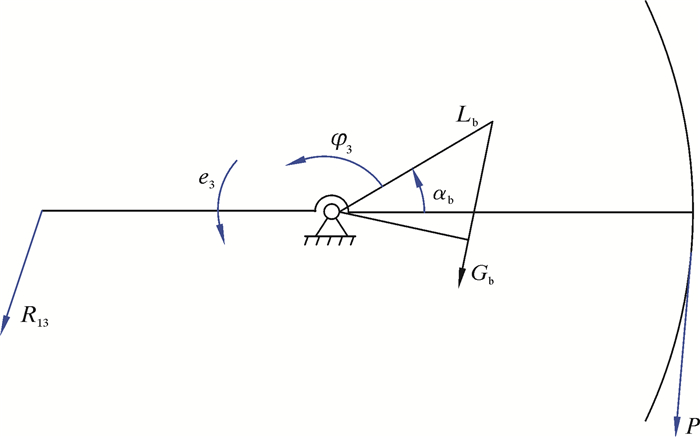
若要计算等效力矩Me,则需要计算抽水机系统的等效驱动力矩Md和等效阻力矩Mr。建立游梁系统受力简图,如图 3所示。
|
| 图 3 抽水机游梁力学模型 Fig.3 Mechanical model of the water pumping system beam |
游梁系统的重心由其位置和整体重力决定,则游梁总成绕回转中心的力矩为[9]:
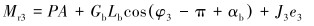
|
(7) |
式中:Mr3为阻力矩,N·m;P为悬点载荷,N;A为游梁前臂长度,m;Gb为游梁系统的重力,N;Lb为游梁系统重心到转动中心的距离,m;φ3为游梁系统的转角,rad;αb为游梁吸引重心和转动中心连线与水平方向夹角,rad;e3为游梁转动的角加速度,rad/s2。
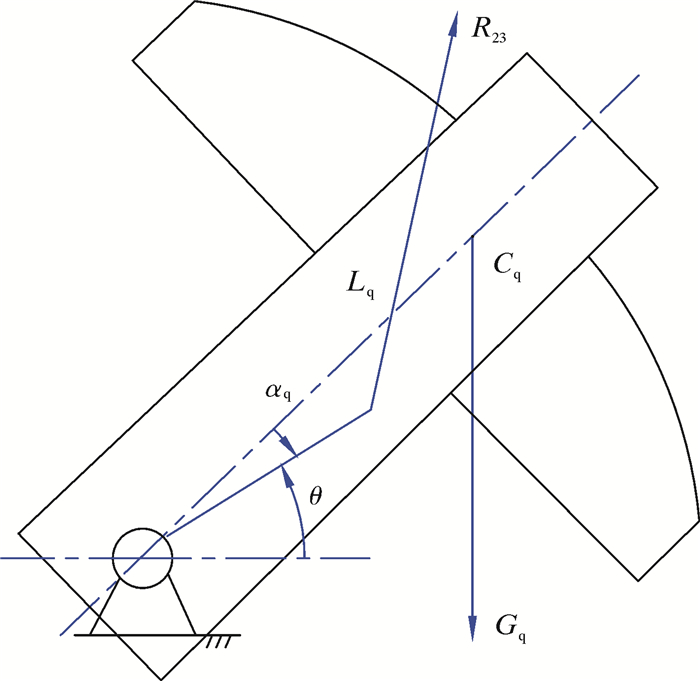
建立曲柄系统受力简图,对曲柄系统进行受力分析,如图 4所示。
|
| 图 4 抽水机曲柄力学模型 Fig.4 Mechanical model of the water pumping system crank |
曲柄系统产生的阻力矩表达式为[9]:
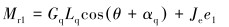
|
(8) |
式中:Mr1为阻力矩,N·m;Gq为曲柄系统的重力,N;Lq为曲柄转动中心到曲柄重心的距离,m;αq为曲柄偏离曲柄系统中线的角度,rad;e1为曲柄转动的角加速度,rad/s2。
系统等效力矩表达式为:
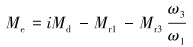
|
(9) |
式中:Me为等效力矩,N·m;i为电机到曲柄的传动比;Md为电机驱动力矩,N·m。
由于Je和Me用解析式表达求解困难,所以用迭代法对方程进行求解[10-11]。用Δθ代替dθ,并且将Je和Me代入公式(5)中,可推导出ωi+1的表达式:
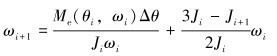
|
(10) |
根据抽水机工况参数,给出等效构件曲柄的初值ω0,就可以求出曲柄任意时刻的角速度ωi。
2.2 Powell优化算法计算示功图电参数与载荷间具备输入输出关系,通过建立电参数与示功图的目标函数,采用Powell算法反演计算悬点示功图。Powell算法是一种局部多参数最优化计算方法,它比全局优化算法有更快的收敛速度。在每一次迭代中,都要从初始点进行一维搜索,搜索方向是Powell算法中的另一个重要参数,用一个多方向集C表示。
Powell算法具体的优化过程分为若干次迭代,每次迭代都由N+1次一维搜索组成,其中N是搜索空间的维度。算法每次迭代过程的步骤是:从初始点开始,依次沿方向集的N个方向进行一维搜索,得到一个最优值及最优值对应的点;沿该点和初始点连线的方向进行搜索,求得本次迭代的最佳值及最佳值对应的点,然后把连线的方向替换前N个方向中效果不好的方向,形成新的方向集,进行下一次迭代[12]。
具体构造过程如下。
(1) 将方向集Ci初始化,Ci=e(i=1, 2,…,N,e为坐标轴的单位向量);
(2) 记录初始点位置P0;
(3) 从Pi出发,以此沿方向集的各个方向寻找该方向归一化互信息的极大值点,记该点为Pi+1,以该点为新的出发点,进行下一次迭代搜索;
(4) 重复步骤(3),直到新点和前一点之间的距离‖Pi+1-Pi‖<ε(ε为设定精度值),该值即为算法的解。
功率测试仪主要用来测量电机的功率,可实现电参数连续、实时测量。实测电机输入功率读取测试数据,取一个完整周期功率数据,对测试数据进行平滑处理。通过动力学方程计算得到曲柄真实角速度,根据曲柄转动一周的时间,得到曲柄角速度与时间的关系,进而将一个周期测试功率与时间的关系转化为功率与角度的关系,便于与计算功率做对比。
根据建立的等效动力学模型计算等效曲柄力矩Me和曲柄真实角速度ω,则可得曲柄功率P。
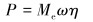
|
(11) |
式中:η为系统总效率;P为计算曲柄功率,W。
建立测试功率与输出功率误差最小的目标函数。采用Powell优化算法,使目标函数最小,优化计算得到示功图。目标函数为:
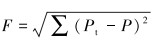
|
(12) |
式中:F为目标函数,Pt为测试功率,W。
Powell算法是以共轭方向为基础寻求最优解的算法[13]。给定初始载荷和误差,采用Powell优化算法进行循环迭代计算,直至满足计算误差要求,计算得到示功图。
3 实例应用中联某抽水机的型号为CYJ12-4.2-73HB,减速器型号为JS-1000,电动机型号为Y280-S, 冲程为4.2 m,冲次1.9 min-1,泵径56 mm,下泵深度1 256 m。实测动液面深度为759 m。
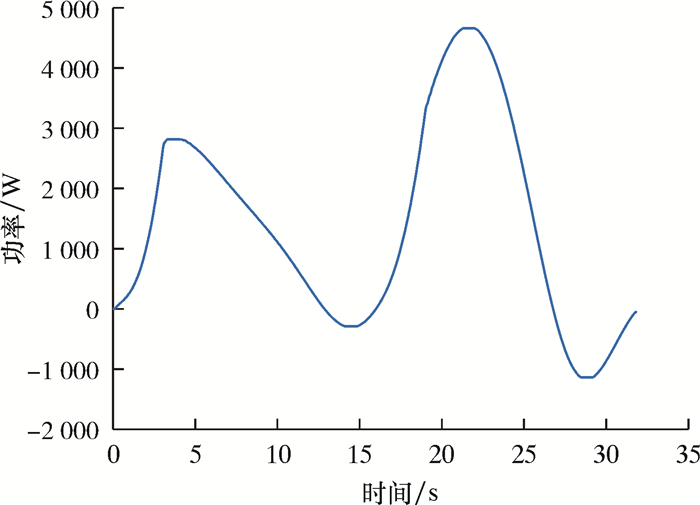
读取测试数据,对测试数据进行平滑处理,得到处理的实测功率曲线如图 5所示。
|
| 图 5 测试功率曲线 Fig.5 Test power |
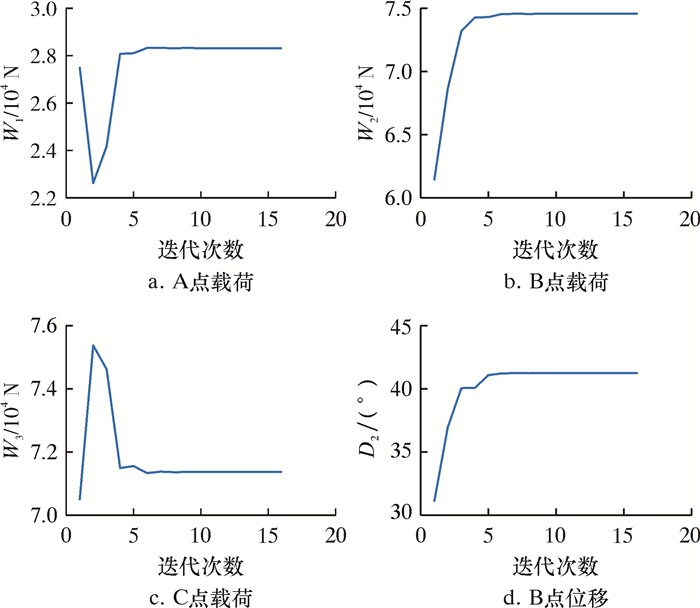
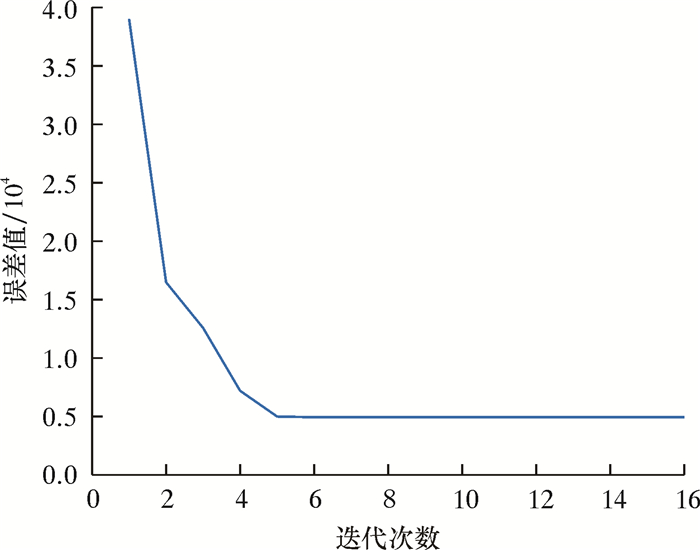
在测得煤层气井驱动电机瞬时功率的条件下,运用等效动力学模型逆分析相关理论,编写MATLAB程序,求解悬点载荷(示功图)。编制Powell算法,以计算功率与实测功率误差最小为目标函数,得到计算结果迭代过程如图 6和图 7所示。
|
| 图 6 悬点载荷迭代过程 Fig.6 Iterative process of the polished rod load |
|
| 图 7 误差迭代过程 Fig.7 Iterative process of the error |
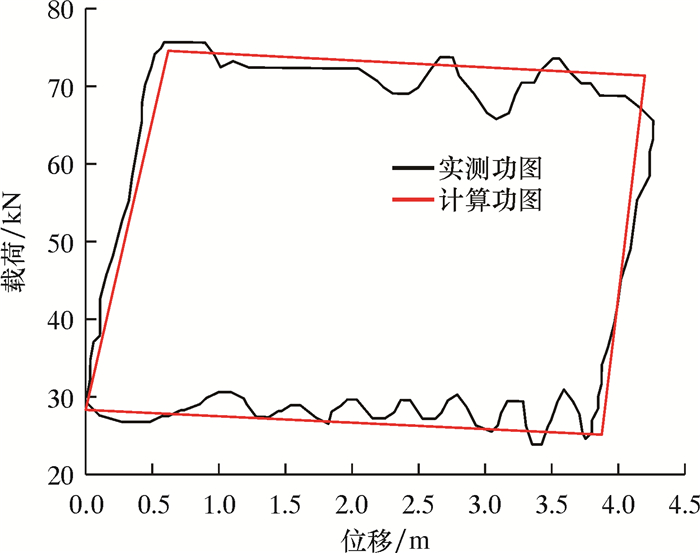
经过Powell优化计算得到悬点载荷后,通过抽水机系统动力学模型计算曲柄真实角速度,由输出扭矩得到曲柄瞬时功率。将计算功率与实测功率曲线进行对比,结果如图 8所示。
|
| 图 8 实测示功图与计算示功图对比 Fig.8 Comparison of measured and calculated indicator diagram |
从图 8可见,计算示功图可以较好地反映实测示功图的简化动力载荷。因此利用Powell算法得到的悬点载荷误差较小。
计算上载荷与下载荷的平均值,其载荷差为11.918 kN, 利用动液面计算模型得到油井深度为738 m,其与实测动液面(深度为759 m)的相对误差为2.77%。
对8口煤层气井进行了计算分析,结果如表 1所示。从表 1可以看出,实测动液面与计算动液面的最大相对误差为8.43%,最小相对误差为1.21%,平均相对误差为4.10%。因此,计算模型能够较准确地计算地面抽水机示功图和煤层气井动液面深度。
| 井号 | 计算动液面深度/m | 实测动液面深度/m | 相对误差/% |
| 1 | 438 | 450 | 2.67 |
| 2 | 326 | 330 | 1.21 |
| 3 | 454 | 490 | 7.35 |
| 4 | 463 | 470 | 1.49 |
| 5 | 467 | 510 | 8.43 |
| 6 | 555 | 565 | 1.77 |
| 7 | 481 | 499 | 3.60 |
| 8 | 505 | 539 | 6.30 |
4 结论
(1) 为了实现动液面的自动实时监测及精确测量,首先建立了动力学模型,其次通过Powell算法得到最优示功图,再结合井筒及环空流体压力分布计算式,建立了基于示功图计算动液面深度的数学模型并将其应用于现场计算。
(2) 经8口不同工况煤层气井的计算分析可得,计算动液面深度与实测动液面深度的最大相对误差为8.43%,最小相对误差为1.21%,平均相对误差为4.10%,计算误差满足工况要求,这表明所建立的计算模型和分析方法可以较准确地求解悬点示功图。
(3) 根据理论示功图计算动液面,消除了动载荷影响,实现了动液面的准确计算。结合电参数反演示功图在线实时采集电参数,可以实现动液面的自动实时监测,提高了煤层气井生产分析的实时性,有利于煤层气田数字化和信息化建设。
| [1] |
赵海晖, 綦耀光, 杜宏伟, 等. 主机构为导杆机构的游梁式抽油机性能分析与评价[J]. 石油钻采工艺, 2016, 38(2): 272-276. ZHAO H H, QI Y G, DU H W, et al. Analysis and assessment on performance of beam pumping units with guide bar mechanism[J]. Oil Drilling & Production Technology, 2016, 38(2): 272-276. |
| [2] |
滕学清, 狄勤丰, 李宁, 等. 超深井钻柱粘滑振动特征的测量与分析[J]. 石油钻探技术, 2017, 45(2): 32-39. TENG X Q, DI Q F, LI N, et al. Measurement and analysis of stick-slip characteristics of drill string in ultra-deep wells[J]. Petroleum Drilling Technique, 2017, 45(2): 32-39. |
| [3] |
张瑞超, 肖良飞, 陈德春, 等. 基于示功图的抽油机平衡诊断与调整[J]. 石油机械, 2018, 46(4): 88-93. ZHANG R C, XIAO L F, CHEN D C, et al. Balance diagnosis and adjustment of pumping unit based on indicator diagram[J]. China Petroleum Machinery, 2018, 46(4): 88-93. |
| [4] |
蒋林.电参数反演抽油机井示功图技术研究[D].成都: 西南石油大学, 2016. JIANG L.The study on electrical parameter inversion of dynamometer card for pumping well[D]. Chengdu: Southwest Petroleum University, 2016. |
| [5] |
任旭虎, 苏建楠, 李旭. 游梁式抽油机多模式控制系统设计与开发[J]. 石油机械, 2018, 46(1): 72-77. REN X H, SU J N, LI X. Design and development of multi-mode control system for beam pumping unit[J]. China Petroleum Machinery, 2018, 46(1): 72-77. |
| [6] |
牛新明, 张进双, 周号博. "三超"油气井井控技术难点及对策[J]. 石油钻探技术, 2017, 45(6): 1-7. NIU X M, ZHANG J S, ZHOU H B. Technological challenges and countermeasures in well control of ultra-deep, ultra-high temperature and ultra-high pressure oil and gas wells[J]. Petroleum Drilling Technique, 2017, 45(6): 1-7. |
| [7] |
高鹏, 常鹏刚, 张胜利, 等. 基于地面功图的功图算产模型建立与应用[J]. 钻采工艺, 2018, 41(2): 51-53. GAO P, CHANG P G, ZHANG S L, et al. Establishment and application of power graph calculation model based on ground power map[J]. Drilling and Production Technology, 2018, 41(2): 51-53. DOI:10.3969/J.ISSN.1006-768X.2018.02.15 |
| [8] |
陈德春, 张瑞超, 孟红霞, 等. 基于功图的油井动液面计算模型及应用[J]. 科学技术与工程, 2015, 15(32): 32-35. CHEN D C, ZHANG R C, MENG H X, et al. The study and application of dynamic model based on dynamometer liquid level calculation card of oil wells[J]. Science Technology and Engineering, 2015, 15(32): 32-35. DOI:10.3969/j.issn.1671-1815.2015.32.006 |
| [9] |
綦耀光, 陈如恒, 丁全祥. 游梁式抽油机运动规律分析[J]. 石油钻采工艺, 1996, 19(2): 49-52. QI Y G, CHEN R H, DING Q X. Analyzed of motion law of beam pumping unit[J]. Oil Drilling & Production Technology, 1996, 19(2): 49-52. |
| [10] |
曲秀全, 焦映厚, 陈照波, 等. 单自由度平面连杆机构等效转动惯量计算公式[J]. 哈尔滨工业大学学报, 2004, 36(5): 610-612. QU X Q, JIAO Y H, CHEN Z B, et al. A calculation method of equivalent moment of inertia for one-DOF planar linkage[J]. Journal of Harbin Institute of Technology, 2004, 36(5): 610-612. DOI:10.3321/j.issn:0367-6234.2004.05.013 |
| [11] |
张元奇, 徐绍堂. 平面四连杆机构等效转动惯量计算公式和应用[J]. 一重技术, 2006(3): 15-17. ZHANG Y Q, XU S T. Calculation formula and application of equivalent rotating inertia for planar four-bar mechanism[J]. Cfhi Technology, 2006(3): 15-17. DOI:10.3969/j.issn.1673-3355.2006.03.007 |
| [12] |
邢正伟, 李海瑛. 改进的Powell医学图像配准算法的应用[J]. 临床影像技术, 2018, 33(9): 65-70. XING Z W, LI H Y. Application of an improved method of Powell algorthm in medical image registration[J]. Clinical Imaging Technology, 2018, 33(9): 65-70. |
| [13] |
孙靖民, 梁迎春. 机械优化设计[M]. 北京: 机械工业出版社, 2006: 83-89. SUN J M, LIANG Y C. Mechanical optimization design[M]. Beijing: Machinery Industry Press, 2006: 83-89. |



