2. 中国石油大学(华东)机电工程学院
2. College of Mechanical and Electronic Engineering, China University of Petroleum(Huadong
0 引言
割缝筛管完井简单快捷,成本优势明显,可以实现快速完井,同时其井身结构简单,在油田生产中得到了广泛应用[1]。油井完井和生产过程中,筛管会受到内部和外部载荷的作用,如果筛管周围或内部堵塞,井眼压力增加,筛管可能被挤毁,因此需要通过试验或数值模拟来研究筛管不同布缝参数下抗内压和外压的情况,以防止筛管损坏[2]。此外,筛管的布缝参数不仅影响筛管的强度,还对过流面积有直接的影响,进而影响油气井的产量。因此,进行筛管布缝参数的研究对于延长筛管的寿命和保证油气井的安全生产具有重要意义[3]。
李航等[4]研究了割缝筛管不同缝槽排列形式筛管抗挤强度的问题;何良等[5]提出了生产压力下割缝筛管的缝宽选择标准;张炜等[6]针对水平井割缝筛管完井参数利用表皮因子进行了优化。从以上研究可以看出,目前针对割缝筛管的优化只采用抗挤强度或者表皮因子单一优化目标进行优化。鉴于此,笔者分别建立了抗挤强度模型及表皮因子模型,将有限元模拟结果与表皮因子计算结果相结合形成多目标优化问题,采用遗传算法进行求解,得到了割缝筛管布缝参数的最优组合。
1 抗挤强度及表皮因子模型的建立 1.1 割缝筛管抗挤强度有限元模型 1.1.1 割缝筛管参数设置选用的割缝筛管外径139.7 mm,壁厚7.7 mm,材料钢级P110,弹性模量206 GPa,泊松比0.3,屈服强度552 MPa,材质为理想弹塑性。在建立模型时,管体长度为外径的8倍[7]左右,缝形分别选择为平行缝、交错缝和螺旋缝。割缝筛管的几何模型如图 1所示。割缝筛管参数:缝宽0.6 mm,缝长80 mm,缝间隔40 mm,周缝数16条/周。

|
| 图 1 割缝筛管的几何模型 Fig.1 Geometric model of a slotted screen |
1.1.2 网格划分
有限元模型采用SOLID45单元。由于割缝处会出现应力集中现象,所以在割缝稀疏的情况下,分别对有割缝区域和无割缝区进行网格划分,在割缝处进行网格加密,以提高计算结果的精度。
1.1.3 约束条件及加载方式在实际工况中通常采用悬挂筛管完井,另一端为自由端,因此在有限元模型中对割缝筛管的一端面施加全约束,内、外表面分别设定工况进行施压。在作业工况下,筛管受外压(大地静压)和内压(流体内压)的影响,因此在建模时要首先设定工况条件再对筛管进行有限元分析。
定义筛管抗挤强度为筛管应力达到屈服应力时所加的外压值。对平行缝、交错缝和螺旋缝进行有限元分析,当割缝筛管最大应力达到材料屈服应力时,即可得出其抗挤强度。
1.2 割缝筛管表皮因子模型油田现场中存在多种完井方式,如裸眼完井、筛管完井、套管完井以及砾石填充完井等。根据油田现场的地层压力、岩石物理特性及地层稳定性等条件,选择合适的完井方式成为亟待解决的重要问题。为解决上述问题,K.FURUI等[8]提出表皮因子模型辅助选择合适的完井方式。表皮因子是通过实际与理论完井方式对比求得的无量纲因子。当表皮因子大于零时,表征完井方式对井下工况产生了一定的破坏,使得油井生产效率降低;当表皮因子小于零时,表征完井方式使得油井生产效率升高。表皮因子计算见式(1)~式(3),具体计算见文献[8]。
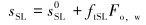
|
(1) |
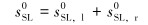
|
(2) |
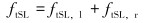
|
(3) |
式中:sSL为割缝筛管表皮因子;sSL0为速率无关表皮因子;ftSL为湍流因子;Fo, w为Forchheimer数;下标l和r表示缝内的线性流和缝外的径向流,不考虑近井地带污染以及储层的非均质性。
本文在计算表皮因子时,取日产液量为10 m3,渗透率为0.3 mD。
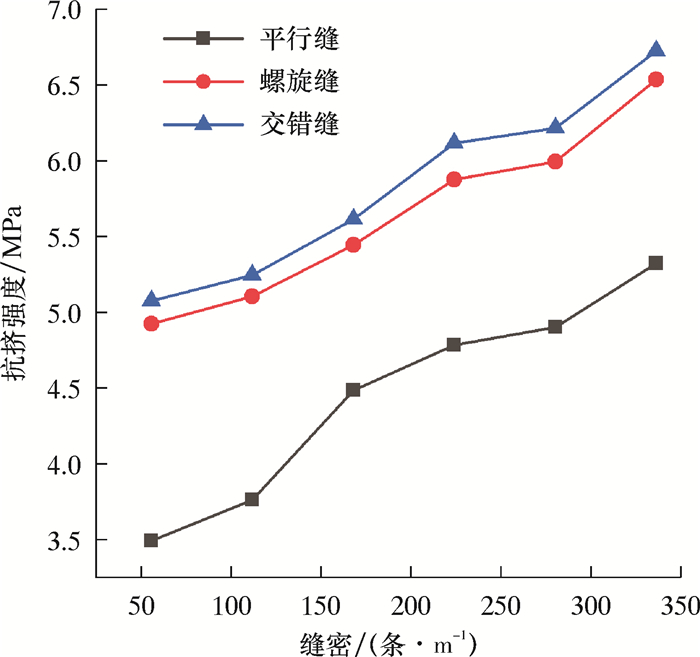
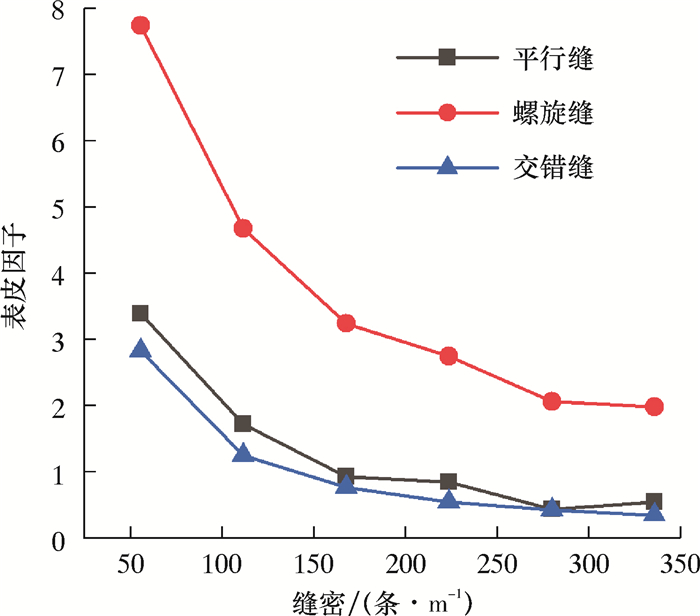
2 缝形优化割缝筛管缝宽为0.6 mm,缝长为80 mm,缝单元内的缝数为1,缝密为56~336条/m,间隔56条/m(保持缝间隔不变,改变周缝数)。抗挤强度仿真结果如图 2所示。表皮因子计算结果如图 3所示。由图 2可以看出,在缝密相同时,交错缝筛管的抗挤强度最高,螺旋缝筛管居中,平行缝的抗挤强度最低,这说明交错缝筛管可有效降低割缝对筛管抗挤强度的影响。由图 3可以看出,在缝密相同时,交错缝的表皮因子最小,其次是平行缝,螺旋缝最大。
|
| 图 2 缝形和缝密对筛管抗挤强度的影响 Fig.2 Effect of slot shape and density on the collapse strength of screen |
|
| 图 3 缝形和缝密对筛管表皮因子的影响 Fig.3 Effect of slot shape and density on the skin factor of the screen |
由以上分析可知,交错缝筛管不仅抗挤强度高,而且表皮因子较低,因此最优缝形为交错缝。
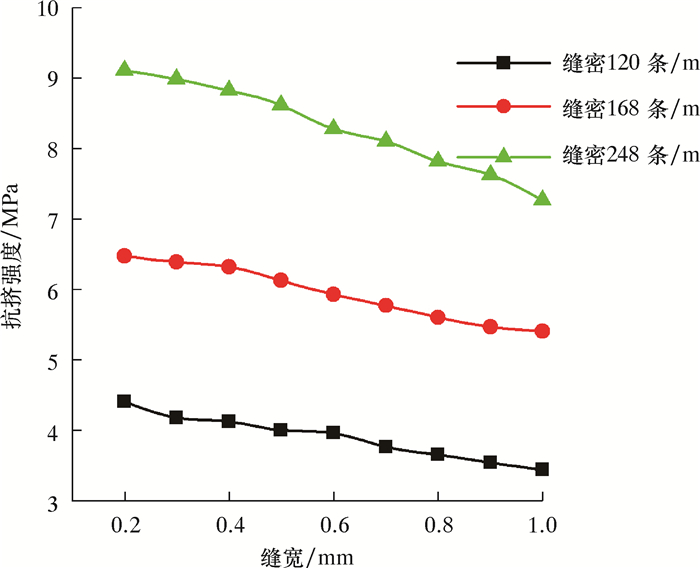
3 交错缝参数敏感性分析 3.1 缝宽设置割缝筛管缝长L=60 mm,缝单元内的缝数为1,缝密分别为120、168和248条/m,缝宽取值范围为0.2~1.0 mm,间隔0.1 mm。抗挤强度计算结果如图 4所示。表皮因子计算结果如图 5所示。
|
| 图 4 缝宽对筛管抗挤强度的影响 Fig.4 Effect of slot width on the collapse strength of screen |
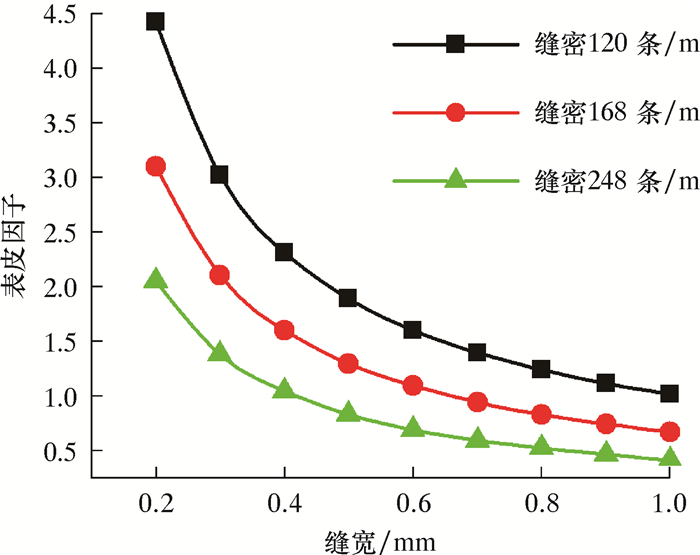
|
| 图 5 缝宽对筛管表皮因子的影响 Fig.5 Effect of slot width on the skin factor of the screen |
由图 4可以看出:随着缝宽的增加,筛管的抗挤强度呈近似线性降低;缝密越大,随着缝宽的增加,抗挤强度降低速度加快;但总体来说,随着缝宽的增加,筛管的抗挤强度降低程度较小。因此,在满足要求的条件下,可采用较大的缝宽。由图 5可以看出:在相同缝密的条件下,割缝筛管表皮因子大小随缝宽的增大而减小;表皮因子的下降速度随着缝密的增加而减小。
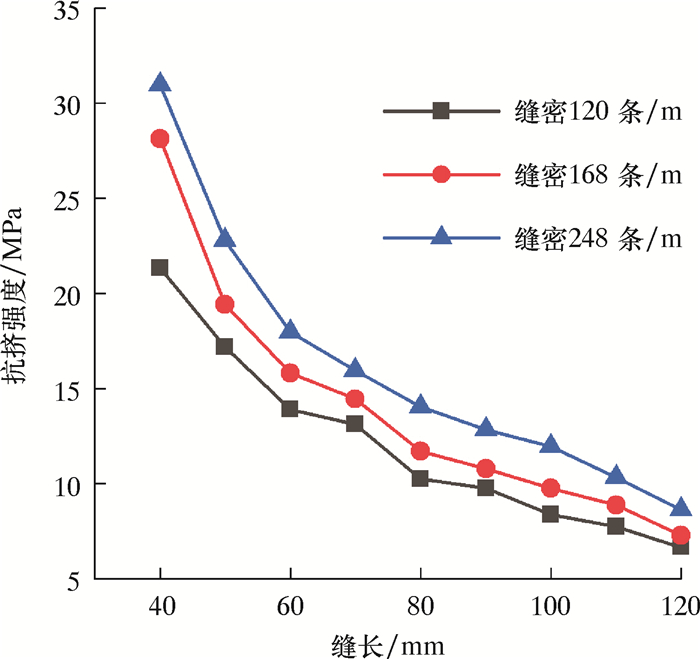
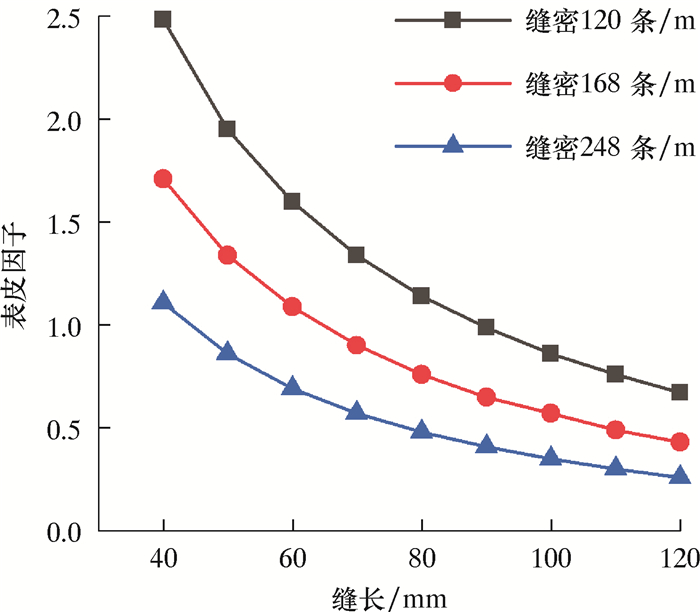
3.2 缝长设置割缝筛管缝宽W=0.6 mm,缝单元内的缝数为1,缝密分别为120、168和248条/m,缝长取值范围为40~120 mm,间隔10 mm。抗挤强度计算结果如图 6所示。表皮因子计算结果如图 7所示。由图 6可以看出:随着缝长的增加,筛管抗挤强度近似呈指数下降;当缝长小于70 mm时,随着缝长的增加,筛管的抗挤强度下降剧烈;当缝长大于70 mm时,抗挤强度下降变缓。因此,选择缝长时,不宜过大。由图 7可以看出:割缝筛管表皮因子随缝长的增大而减小;表皮因子的下降速度随着缝密的增加而减小。
|
| 图 6 缝长对筛管抗挤强度的影响 Fig.6 Effect of slot length on the collapse strength of screen |
|
| 图 7 缝长对筛管表皮因子的影响 Fig.7 Effect of slot length on the skin factor of the screen |
3.3 缝密
由图 2可以看出,随着缝密的增加,筛管的抗挤强度有所增加,因为周缝数增加,应力分布更均匀,应力集中现象有所缓解。由图 3可以看出,随着缝密的增加,表皮因子随着缝密的增加而减小,因为周缝数增加,过流面积变大,油井生产效率提高。
4 交错缝筛管参数优化设计 4.1 响应曲面试验设计将缝密进一步分解为周缝数和缝间隔两个参数。采用响应曲面试验设计分析,对筛管的抗挤强度σ、表皮因子sSL、缝宽W、缝长L、周缝数N和缝间隙S之间的函数关系进行逼近。由于不清楚各个因素之间是否存在交互关系,为保证模型的准确性,本文采用面心组合设计的二阶模型[9]:
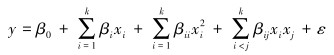
|
(4) |
式中:β0为回归常数,xi、xj为自变量,βi、βii和βij分别表示一次、二次及交互作用项的回归系数,ε为误差。
为进一步保证模型的准确性,采用5水平进行试验设计,采用正交试验的方法进行仿真计算,得到的试验结果如表 1所示。
| W/mm | L/mm | N | S/mm | σ/MPa | sSL |
| 0.2 | 40 | 7 | 10 | 13.27 | 5.72 |
| 0.2 | 60 | 14 | 20 | 10.54 | 2.97 |
| 0.2 | 80 | 21 | 30 | 10.11 | 1.98 |
| 0.2 | 100 | 28 | 40 | 7.99 | 1.47 |
| 0.2 | 120 | 35 | 50 | 6.43 | 1.15 |
| 0.4 | 40 | 14 | 30 | 24.93 | 2.05 |
| 0.4 | 60 | 21 | 40 | 16.69 | 1.25 |
| 0.4 | 80 | 28 | 50 | 9.06 | 0.87 |
| 0.4 | 100 | 35 | 10 | 6.85 | 2.91 |
| 0.4 | 120 | 7 | 20 | 4.68 | 0.42 |
| 0.6 | 40 | 21 | 50 | 29.66 | 1.19 |
| 0.6 | 60 | 28 | 10 | 15.43 | 0.40 |
| 0.6 | 80 | 35 | 20 | 16.03 | 0.32 |
| 0.6 | 100 | 7 | 30 | 6.50 | 2.30 |
| 0.6 | 120 | 14 | 40 | 4.42 | 1.00 |
| 0.8 | 40 | 28 | 20 | 36.84 | 0.42 |
| 0.8 | 60 | 35 | 30 | 25.16 | 0.31 |
| 0.8 | 80 | 7 | 40 | 10.62 | 2.14 |
| 0.8 | 100 | 14 | 50 | 8.95 | 0.90 |
| 0.8 | 120 | 21 | 10 | 7.16 | 0.32 |
| 1.0 | 40 | 35 | 40 | 44.29 | 0.36 |
| 1.0 | 60 | 7 | 50 | 15.90 | 2.17 |
| 1.0 | 80 | 14 | 10 | 11.73 | 0.50 |
| 1.0 | 100 | 21 | 20 | 11.17 | 0.30 |
| 1.0 | 120 | 28 | 30 | 10.51 | 0.19 |
通过变量代换,将多元非线性二阶模型转化为多元线性一阶模型,然后进行多元线性回归分析,可分别建立因子(缝宽、缝长、周缝数和缝间隔)与响应值(抗挤强度和表皮因子)之间的多元回归方程。
抗挤强度:
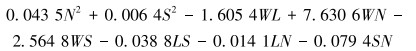
|
(5) |
表皮因子:

|
(6) |
用于产油井的割缝筛管不仅要考虑筛管的抗挤强度,还要考虑筛管的表皮因子大小。故本文将割缝筛管抗挤强度与表皮因子综合考虑,形成多目标优化问题,采用遗传算法计算得到割缝筛管参数的最优组合。
4.2.1 设计变量割缝筛管的设计变量为缝长、缝宽、缝间隔和周缝数,将其视为设计变量矩阵,即有:
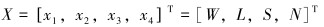
|
(7) |
上述变量采用二进制编码以表示相应的“染色体”。除了变量之外,根据产油井的优化目标,构建遗传算法所需的适应度函数。其中,抗挤强度最大优化目标如式(8)所示。
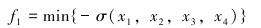
|
(8) |
表皮因子最小优化目标如式(9)所示。
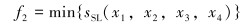
|
(9) |
割缝筛管的最大作用是阻止砂粒进入筛管,因此缝宽应小于设计砂粒直径。为保证正常采油时抽油泵正常运行,允许进入泵内的砂粒直径最大为1 mm,即缝宽约束为:
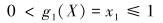
|
(10) |
根据现场经验,为保证筛管抗挤强度,割缝的最大长度为120 mm,即有:
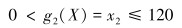
|
(11) |
周缝数与缝宽的乘积小于筛管外径周长,且周缝数为正整数,即有:
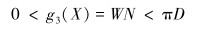
|
(12) |
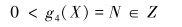
|
(13) |
缝间隔约束为:
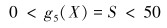
|
(14) |
根据优化变量、优化目标和约束条件,割缝筛管的多目标优化数学模型如式(15)所示。
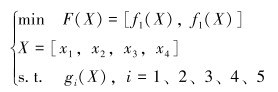
|
(15) |
采用MATLAB的gamultiobj[10]对上述数学模型进行求解。首先,将群体设置为double vector类型,群体数量定为100,采用非线性自适应函数生成相应的群体,对初始群体的取值采用缺省设置。其次,采用轮盘赌选择法进行染色体选择,采用自定义突变法进行变异,采用二进制两点交叉。计算终止条件采用缺省设置,最大迭代步数设为200。
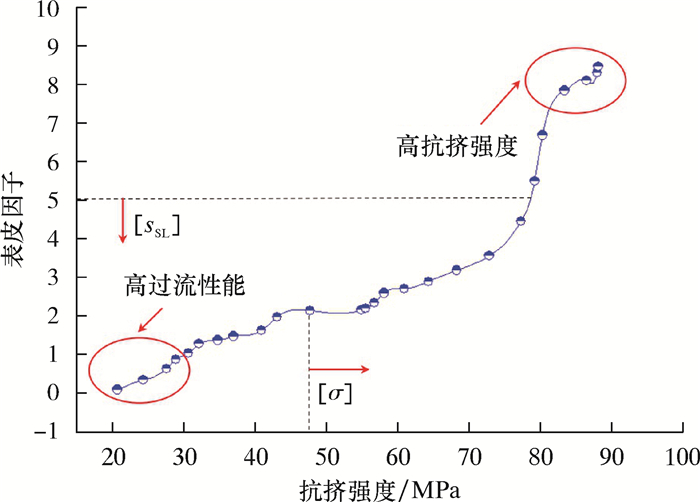
4.2.6 优化结果优化后得到12组最优解,优化结果如表 2及图 8所示,分为低表皮因子和高强度两种类型。
|
| 图 8 割缝筛管多目标优化结果 Fig.8 Multi-objective optimization results of slotted screen |
| 缝宽/ mm |
缝长/ mm |
缝间隔/ mm |
周缝数/ 周 |
抗挤强 度/MPa |
表皮因子 |
| 0.1 | 80 | 10 | 50 | 88.10 | 8.45 |
| 0.1 | 90 | 10 | 50 | 87.90 | 8.29 |
| 0.1 | 100 | 10 | 50 | 86.44 | 8.08 |
| 0.1 | 110 | 10 | 50 | 83.36 | 7.83 |
| 0.3 | 10 | 10 | 50 | 80.25 | 6.67 |
| 0.5 | 10 | 10 | 50 | 79.16 | 5.49 |
| 0.7 | 10 | 10 | 50 | 77.25 | 4.45 |
| 0.9 | 10 | 10 | 30 | 58.07 | 2.60 |
| 0.9 | 10 | 10 | 50 | 72.84 | 3.56 |
| 0.9 | 10 | 20 | 40 | 54.93 | 2.16 |
| 0.9 | 10 | 20 | 45 | 55.53 | 2.20 |
| 0.9 | 10 | 20 | 50 | 56.75 | 2.34 |
由图 8可以看出,优化结果分为两类:一是高抗挤强度型,二是高过流性能(低表皮因子)。现场应用时,要根据具体的地层情况和使用要求进行最终参数组合的选取。对于产液量高的井,可在保证筛管满足最低抗挤强度[σ]的情况下使得筛管有较低的表皮因子(尽可能高的过流性能)的参数组合;对于较深的井,可在保证最高表皮因子[sSL]前提下使得筛管有尽可能大的抗挤强度。由表 2可以看出,大缝宽和小缝长或小缝宽和大缝长组合以及高缝密、小间隔的筛管有较好的抗挤性能和过流性能。
5 结论(1) 建立了割缝筛管抗挤强度有限元模型以及表征其通流性能的表皮因子模型,对交错缝、螺旋缝和平行缝三种缝形进行了优选,结果表明交错缝筛管同时具有良好的抗挤强度和通流性能。
(2) 对交错缝筛管进行了参数敏感性分析,结果表明:表皮因子和抗挤强度均随缝宽和缝长的增加而减小;抗挤强度随缝密的增加而增加,表皮因子随缝密的增加而减小。
(3) 对交错型筛管进行了多目标优化,得到最优解集,选择大缝宽和小缝长或小缝宽和大缝长组合以及高缝密、小间隔的筛管有较好的抗挤性能和过流性能。
| [1] |
齐月魁, 刘艳红. 水平井割缝筛管完井技术应用[J]. 钻采工艺, 2000, 23(5): 98-100. QI Y K, LIU Y H. Application of slotted screen completion technology in horizontal wells[J]. Drilling and Production Technology, 2000, 23(5): 98-100. DOI:10.3969/j.issn.1006-768X.2000.05.032 |
| [2] |
杨晓东, 戴华林, 孙立瑛. 割缝筛管抗挤压强度综合因素有限元分析[J]. 石油钻采工艺, 2009, 31(5): 40-44. YANG X D, DAI H L, SUN L Y. Finite element analysis on the comprehensive factors of slotted liner collapsing strength[J]. Oil Drilling and Production Technology, 2009, 31(5): 40-44. DOI:10.3969/j.issn.1000-7393.2009.05.010 |
| [3] |
刘大红, 宋秀英, 刘艳红, 等. 割缝筛管防砂设计及应用[J]. 石油机械, 2004, 32(8): 13-16. LIU D H, SONG X Y, LIU Y H, et al. Design and application of slotted screen pipe for sand control[J]. China Petroleum Machinery, 2004, 32(8): 13-16. DOI:10.3969/j.issn.1001-4578.2004.08.005 |
| [4] |
李航, 邱亚玲, 伍建川, 等. 不同布缝形式的割缝筛管抗挤强度有限元分析[J]. 石油机械, 2016, 44(2): 80-83. LI H, QIU Y L, WU J C, et al. Finite element analysis on the collapsing strength of slotted liner with different slot arrangement[J]. China Petroleum Machinery, 2016, 44(2): 80-83. |
| [5] |
何良, 邓福成, 谭章龙, 等. 基于生产压力下割缝筛管的缝宽选择标准[J]. 科学技术与工程, 2018, 18(21): 200-205. HE L, DENG F C, TAN Z L, et al. Standard for selection of slot width of slotted screen based on working pressure[J]. Science Technology and Engineering, 2018, 18(21): 200-205. DOI:10.3969/j.issn.1671-1815.2018.21.031 |
| [6] |
张炜, 方全堂, 朱春林. 水平井割缝筛管完井参数优化模型[J]. 油气田地面工程, 2014, 33(2): 10-11. ZHANG W, FANG Q T, ZHU C L. Optimization model of completion parameters of sieve pipe in horizontal wells[J]. Oil-Gas Field Surface Engineering, 2014, 33(2): 10-11. DOI:10.3969/j.issn.1006-6896.2014.2.006 |
| [7] |
杨睿月, 黄中伟, 李根生, 等. 煤层气水平井割缝筛管优化设计[J]. 煤炭学报, 2014, 39(11): 2269-2275. YANG R Y, HUANG Z W, LI G S, et al. Optimization design for the geometry parameters of slotted liner in coalbed methane horizontal wells[J]. Journal of China Coal Society, 2014, 39(11): 2269-2275. |
| [8] |
FURUI K, ZHU D, HILL A D. A comprehensive skin-factor model of horizontal-well completion performance[R]. SPE 84401-PA, 2005.
|
| [9] |
吕孝孝, 刘延鑫, 王旱祥, 等. 底水油藏单管排水采油工艺研究及其管柱优化[J]. 石油机械, 2017, 45(9): 80-86. LÜ X X, LIU Y X, WANG H X, et al. Single tube water drainage and oil production technology for bottom water reservoir and its jet pipe optimization[J]. China Petroleum Machinery, 2017, 45(9): 80-86. |
| [10] |
张建乔, 刘永红, 吕广忠, 等. 基于混合遗传算法的新型防砂筛管优化设计[J]. 机械设计, 2005, 22(9): 20-23. ZHANG J Q, LIU Y H, LÜ G Z, et al. Optimization design of new anti-sand sieve tube based on hybrid genetic algorithm[J]. Journal of Machine Design, 2005, 22(9): 20-23. |


