2. 中国石油集团海洋工程有限公司钻井事业部
2. Drilling Division of CNPC Offshore Engineering Company Limited
0 引言
目前,各大科研机构及相关企业都在探讨深海S型铺管法的可行性,该方法具有对船只发动机动力需求低、相比J型铺设法残余应力小等优势,逐步得到工程技术人员的认可[1-3]。现有研究主要分为以下两个方向:一是提出管道形态的微分方程,随后对管道整体进行有限元分析,将理论与数值模拟相结合;二是在实验室创建托管架实物模型,设置模型的控制系统和数据采集系统,施加载荷及振动,对试验结果进行分析[4-8]。上述研究并未深入探讨托管架系统的调整原理和方法,当铺设海况发生改变时,托管架的入水角度与各托辊的支撑位置无法得到正确调整。一旦投产深海S型铺设托管架,其支撑的海底管道应力可能大于屈服极限,影响作业效率和铺管安全。因此,对托管架系统的调整方法进行科学研究很有必要。
深海海况较为复杂,托管架系统需要及时调整。然而,传统方法计算效率低,难以满足实际工程需要;现有铺管作业分析软件多由企业自行研发,多数软件对外保密,并且通用性较差。为此,有必要根据托管架调整理论进行编程,开发一款软件,将监测数据导入软件进行分析,使托管架系统得以及时调整,同时保证铺管作业的安全。
1 深海铺管船托管架系统调整分析 1.1 托管架管段入水角度调整当铺管作业环境发生改变时,根据自然悬链线理论,海底管道形态会发生变化。为了保证管道和铺管作业的安全,需要调整托管架管段的入水角度,其值与脱离点的角度相同。S型铺管法原理如图 1所示,脱离点是管道脱离托管架的节点,是S型铺管3个重要的节点之一。
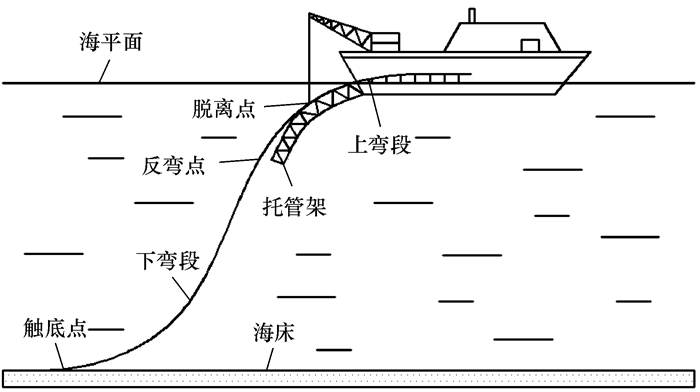
|
| 图 1 S型铺管法原理图 Fig.1 Schematic diagram of S-laying method |
为了确定脱离点的数值,使托管架得以调整,需要对管道铺设线型进行分析[9-10]。如图 2所示,以触底点为坐标原点O建立平面直角坐标系,A为脱离点,管线任意位置与水平方向的夹角为θ。在管道下弯段中,脱离点处受到沿轴向的张紧力T,触底点处受到海床施加的水平方向力H。在不考虑其他压力的情况下,这两点之间的管段仅受到海水的浮力和重力作用,其方向竖直向上[11]。
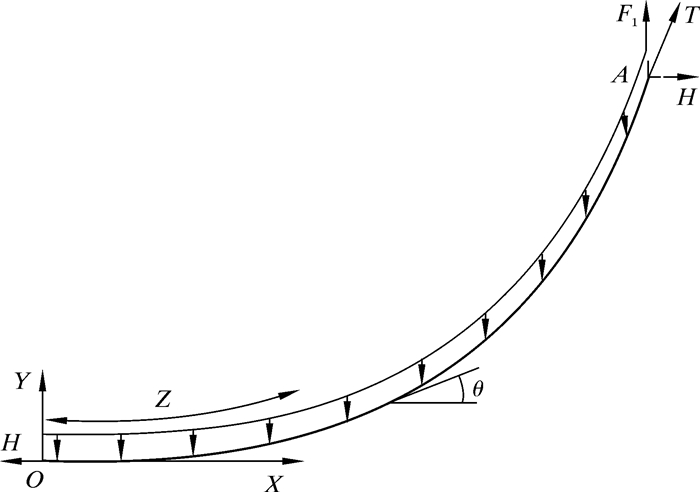
|
| 图 2 下弯段管道线型 Fig.2 Profile of the lower bend pipeline |
管道线型的模拟通常采用自然悬链线法,该方法需要将处理的模型进行整体分析。下弯段管道线型可由式(1)所示的悬链线方程表示:
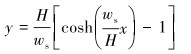
|
(1) |
式中:x、y分别表示管道任意一点的横、纵坐标,即相对于触底点的水平与竖直距离;ws表示管道在水中单位长度的浮重;H表示在触底点处受到的水平作用力。
值得注意的是,需要参考铺管船的动力性能来选取水平力H的大小,其上限不可超过铺设作业时铺管船的推进能力极值。
浮重的计算方法为:
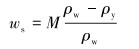
|
(2) |
式中:M表示物体在空气中的质量,ρw表示物体的密度,ρy表示所处液体的密度。
任意一点的曲率可表示为:
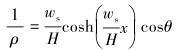
|
(3) |
对式(3)进行分析,当x=0,θ=0(即触底点处)时管道曲率最大,表示为:
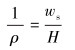
|
(4) |
下弯段管道的总长度L可用水平力、水深及每单位长度的浮重来表示,即有:
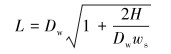
|
(5) |
脱离点处管道受到的张紧力竖直分量表示为:
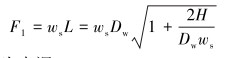
|
(6) |
式中:Dw为水深。
根据式(1)~式(6),下弯段管道在脱离点处的角度可表示为:
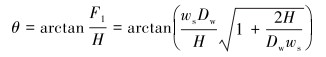
|
(7) |
得知下弯段管道的脱离角度,就可确定工程实际中托管架入水管段与海平面的夹角,使管道以合理的形态铺入海底。
1.2 托辊支撑位置调整托管架各个管段上设有托辊,用以支撑进行铺设的管道。进行铺设作业的管道紧压在托管架上,故海底管道与托管架管段的弯曲半径相同。当托管架管段进行入水角度调整时,若托辊支撑位置不变,不能保证海底管道受力的均匀分布,可能导致局部管道的应力与弯矩集中。因此,托辊支撑位置的相关研究也是保证管道铺设安全的重要因素[12-13]。
托辊支撑位置与其相接触的海底管道构型密切相关,海底管道在安全范围内允许的最小弯曲半径Rmin计算式为:
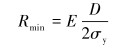
|
(8) |
式中:σy为屈服应力,E为管道所用材料的弹性模量,D为海底管道的外径。
为了获取托辊支撑管道的最优位置,编制了托辊最优支撑位置算法。整体思路为:预先获取托辊支撑坐标区间范围,利用程序求解托辊支撑最优位置,绘制各托辊最优位置坐标拟合曲线;随后,对各托辊最优位置处的曲率半径进行分析,若比Rmin小,说明该处托辊支撑的管道曲率较大,仍会导致局部应力与弯矩集中现象发生,影响管道安全。需将不合理的托辊位置区间进行调整,使管道曲率符合要求。
通过曲线拟合的方法调节托辊位置坐标,使各托辊所支撑的海底管道曲率半径符合要求,保证其弯曲应力在安全范围内。根据铺管船的实际作业情况,可对托辊高低坐标区间进行调整,使其具有较高的应用价值。
2 基于MATLAB GUI的软件实现方法 2.1 软件开发概述铺管作业处于复杂多变的海洋环境中,是一个动态问题,需要根据实时海洋环境载荷进行分析。然而,传统纸笔计算或在MATLAB命令窗口中进行计算效率低下、工作量大,托管架入水的角度及托辊支撑位置不能得以及时调整,在海况明显变化时可能导致较为严重的安全事故。因此,工程上亟需找到一种效率高、操作简便和交互性强的计算方法。
GUI模块是MATLAB公司开发的图形用户界面,其由窗口、菜单、图标、光标及按键等各种图形对象组成。GUI模块为用户提供了一种新型交互界面,计算简单、交互性强,用户可以利用鼠标或键盘选择界面中的图形对象,使计算机进行相应操作。GUI模块的特点满足工程实际需要,故采用MATLAB GUI对托管架调整作业进行软件开发具有较强的科学性及较高的应用价值[14-15]。
2.2 软件构建与封装软件主要功能为:进行托管架入水角度与海底管道线型确定、托辊最优支撑位置分析,在各个界面中根据用户指令进行数据运算及图像绘制。根据实现功能,将软件划分为4个GUI界面:登录界面、管道线型模拟界面、托辊位置优化界面及退出界面。依据前文的有关理论编制程序,在各个界面构建、调试完毕后,要对其进行封装,生成可执行文件,使系统以软件(.exe)的形式展现在用户面前。软件各界面主要功能如图 3所示。
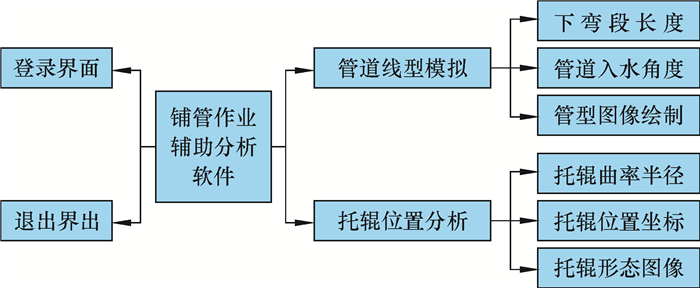
|
| 图 3 软件各界面主要功能 Fig.3 Main functions of each interface of the software |
在命令行窗口中输入“deploytool”,选择Application Compiler封装方法,在各个命令栏填入相应文件,点击封装键,系统随即自动进行托管架调整作业软件的封装工作。一段时间后,系统提示封装完成,技术人员即可打开生成的软件进行操作。
2.3 管道线型模拟界面为了保护用户隐私、使软件更加人性化,运行软件首先弹出登录界面,输入用户名及相应密码,只有密码正确才可进入软件的管道线型模拟界面(见图 4)。如图 4所示,本界面根据1.1节的相关理论进行编程,可完成海底管道下弯段长度计算、线型绘制和托管架管段入水角度调整工作。界面上方为菜单栏,点击各个选项,可跳转至相应界面。
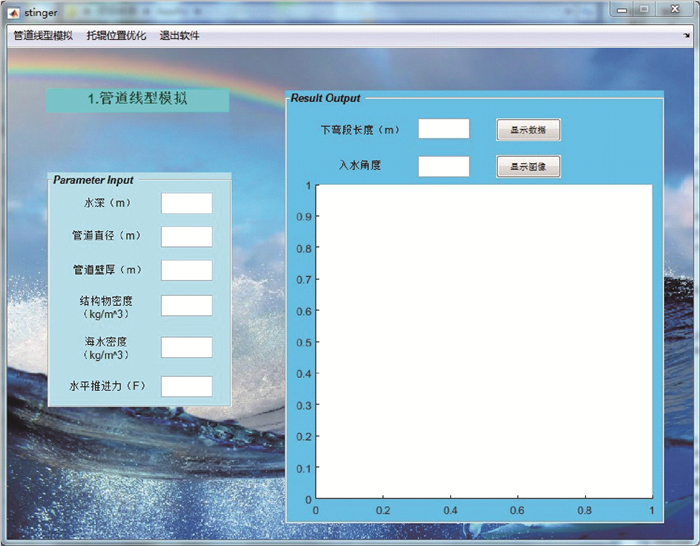
|
| 图 4 管道线型模拟界面 Fig.4 Pipeline profile simulation interface |
当海洋环境发生改变时,海洋铺管作业方可根据最新监测数据,对界面参数输入栏中的水深和水平推进力等参数进行修改,计算此时的管道下弯段长度和入水角度,使托管架入水管段得以调整。若求解完毕,点击菜单栏中的“托辊位置优化”选项,即可进入下一界面。
2.4 托辊位置分析界面如图 5所示,本界面根据1.2节的相关理论进行编程,可完成托辊最优支撑位置横纵坐标及弯曲半径计算、托辊位置拟合图像绘制工作。
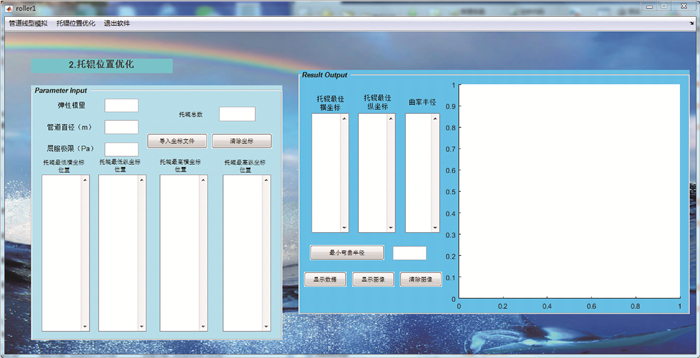
|
| 图 5 托辊位置优化界面 Fig.5 Roller position optimization interface |
为了进行分析与计算,在左侧参数输入栏中需要填入管道的弹性模量、管径和屈服极限,随后导入托辊高低区间坐标文件(本步需要进入托管架托辊安装车间,获取每组托辊初步拟定的最高、最低位置范围),导入的文件内容会随即显示在坐标栏中;若托辊数量较少,可直接在坐标栏中写入相关横纵坐标值。点击右侧参数输出栏的“显示数据”与“显示图像”可得到求解结果。
3 工程算例作为示例,笔者选择X60钢作为海底管道材料,根据某次海上铺管作业的监测情况,利用本软件的两个界面完成对托管架系统的调整。进入系统后,首先打开管道线型模拟界面,在界面左侧参数输入栏中填入相关参数。表 1为管道的模拟参数。
| 水深/m | 管径/m | 壁厚/m | 结构密度/ (kg·m-3) |
水体密度/ (kg·m-3) |
水平分 力/kN |
| 900 | 0.16 | 0.02 | 7 850 | 1 030 | 200 |
点击“显示数据”按钮,软件会进行分析,将海底管道下弯段长度和入水角度值相应地显示在求解框中。点击“显示图像”按钮,右下方会显示管道下弯段模拟图像,可更直观地了解下弯段管道线型及相关参数。本例下,由托管架支撑的海底管道下弯段长度为1 404.8 m,托管架管道的入水角度为59.3°。如图 6所示,虚线是对下弯段海底管道的模拟情况。技术人员可综合上述分析对托管架系统进行及时调整。
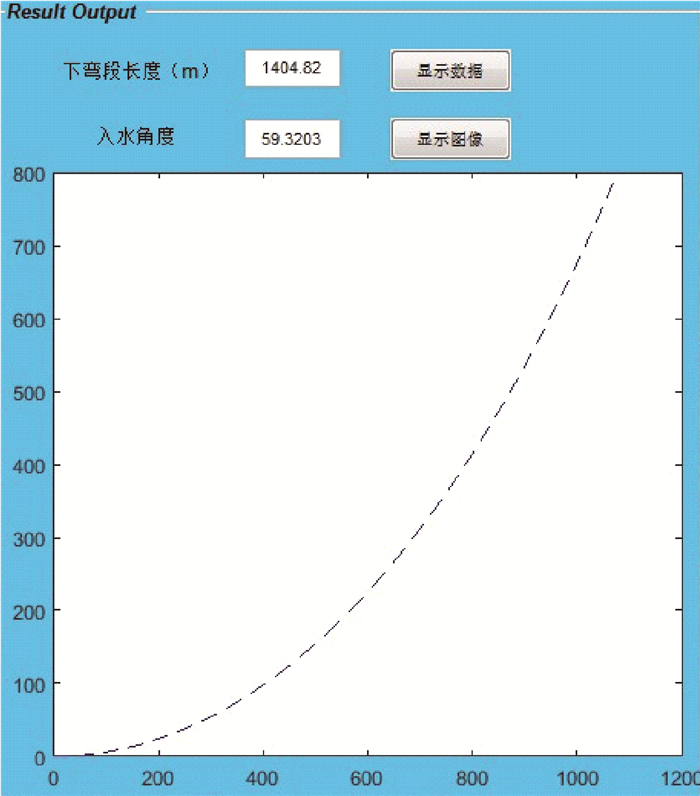
|
| 图 6 管道模拟计算与图像显示 Fig.6 Pipeline simulation calculation and image display |
在管道线型模拟界面打开菜单栏中的“托辊位置优化”,进入该界面。管道的弹性模量、管径、屈服极限以及托辊区间输入情况如图 7所示。
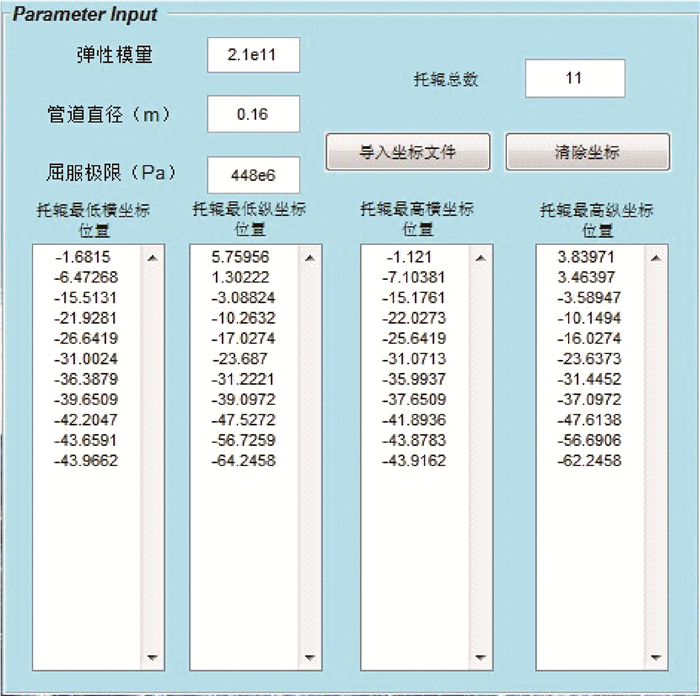
|
| 图 7 管道与托辊位置参数输入 Fig.7 Pipeline and roller position parameters input |
分析结果如图 8所示。图 8中,为了直观地显示托辊位置分布,点击“显示图像”按钮,界面会将托辊位置拟合图像显示在绘图栏中。图中红线为优化后的托辊走向图,圆圈为各托辊实际位置,红“×”和黑“×”分别代表优化前托辊最高和最低位置。
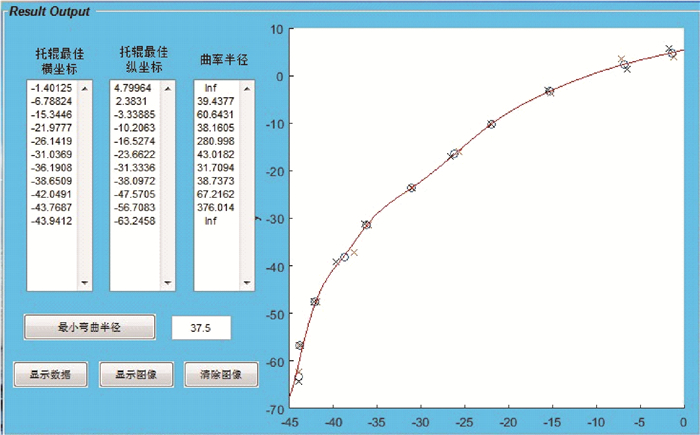
|
| 图 8 托辊位置优化参数与图像显示 Fig.8 Roller position optimization parameters and image display |
按照1.2节的方法,要对各托辊曲率半径与海底管道在安全范围内允许的最小弯曲半径Rmin进行比较。本算例中,第7处托辊曲率半径小于Rmin,为了防止屈服现象产生,需要结合工程实际,调整该托辊位置区间范围,直至满足要求为止。当海况发生改变时,点击界面中的“清除坐标”和“清除图像”按钮,以便导入最新监测参数值,随后再次进行分析。
分析完毕,点击菜单栏的退出软件选项,即退出软件。
4 结论(1) 在现有铺管船托管架系统研究的基础上,提出基于深海S型铺管的托管架调整方法;据此对深海作业的托管架系统进行入水角度和托辊位置调整,为深海铺管作业提供了理论依据。
(2) 借助MATLAB软件GUI模块开发了一款通用性软件,着力提高深海作业时托管架系统调整工作的质量与效率;软件可及时提供最新参数与模拟图像,提高托管架系统及铺管船只在复杂多变的深海环境中的适应能力。
(3) 该软件的开发弥补了海洋管道铺设领域相关分析软件的缺乏或不足;其操作简单、界面友好、交互性强,可根据实际工程需要调整或增加相关计算界面,为托管架的调整工作提供了科学依据及工程应用基础。
| [1] |
甄国强, 胡宗武. 铺设过程中海底管线的非线性分析[J]. 海洋工程, 1993, 11(3): 28-38. ZHEN G Q, HU Z W. Nonlinear analysis of marine pipeline during laying[J]. The Ocean Engineering, 1993, 11(3): 28-38. |
| [2] |
龚顺风, 陈源, 金伟良, 等.深水海底管线S型铺设形态分析[C]//第十四届中国海洋(岸)工程学术讨论会论文集(上册).南京: 中国海洋学会海洋工程分会, 2009: 129-132. GONG X F, CHEN Y, JIN W L, et al.Morphological analysis of S-lay method for deepwater submarine pipeline[C]//The Fourteenth Chinese Marine (Bank) Engineering Symposium. Nanjing: Ocean Engineering Society of Chinese Society of Oceanography, 2009: 129-132. |
| [3] |
LI X H, CHEN G M, ZHU H W, et al. Quantitative risk assessment of submarine pipeline instability[J]. Journal of Loss Prevention in the Process Industries, 2017, 45(1): 108-110. |
| [4] |
姜锡肇, 李志刚, 岳前进, 等. 先进深水S型铺管船及其深海开发应用前景分析[J]. 船舶工程, 2012, 34(2): 87-90. JIANG X Z, LI Z G, YUE Q J, et al. Advanced S-lay pipe-laying vessel and its prospect of application in deepwater[J]. Ship Engineering, 2012, 34(2): 87-90. DOI:10.3969/j.issn.1000-6982.2012.02.024 |
| [5] |
陈凯, 段梦兰, 张文. 深水S型铺管管道形态及力学分析方法研究[J]. 力学季刊, 2011, 32(3): 353-359. CHEN K, DUAN M L, ZHANG W. On Configuration and mechanical analysis method for deepwater S-lay subsea pipeline[J]. Chinese Quarterly of Mechanics, 2011, 32(3): 353-359. |
| [6] |
ZHANG X F, YUE Q J, ZHANG W S, et al. Study on the design of a model experiment for deep-sea S-laying[J]. Ocean Engineering, 2014, 84(4): 194-200. |
| [7] |
竺艳蓉. 海洋工程波浪力学[M]. 天津: 天津大学出版社, 1991. ZHU Y R. Wave mechanics of oceanographic engineering[M]. Tianjin: Tianjin University Press, 1991. |
| [8] |
姚文伟.桩基结构物波浪力的工程计算方法[D].上海: 上海交通大学, 2009. YAO W W. An engineering approach for computation of wave loads on pile-slab structures[D].Shanghai: Shanghai Jiao Tong University, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D069244 |
| [9] |
BAI Y, BAI Q. Subsea pipelines and risers[M]. [S.l.]: Elsevier Science Limited, 2005.
|
| [10] |
王林.深海托管架概念设计要素研究[D].大连: 大连理工大学, 2008. WANG L.Conceptual design essentials of the stinger for deepwater[D].Dalian: Dalian University of Technology, 2008. http://cdmd.cnki.com.cn/article/cdmd-10141-2009207049.htm |
| [11] |
BAYER V, DORKA U E, FULLEKRUG U, et al. On real-time pseudo-dynamic sub-structure testing:algorithm, numerical andresults[J]. Aerospace Science and Technology, 2005, 9(3): 223-232. DOI:10.1016/j.ast.2005.01.009 |
| [12] |
陈凯.深水海底管线S型铺设分析方法与力学特性研究[D].上海: 复旦大学, 2011. CHEN K.On analysis method and mechanical characteristics of S-lay for deepwater subsea pipeline[D].Shanghai: Fudan University, 2011. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D396695 |
| [13] |
XIE P, ZHAO Y, YUE Q J, et al. Dynamic loading history and collapse analysis of the pipe during deepwater S-lay operation[J]. Marine Structures, 2015, 40: 183-192. DOI:10.1016/j.marstruc.2014.11.003 |
| [14] |
HUGUES G, MARION G, OLIVIER C. Developments for the matlab contsid toolbox[J]. IFAC Proceedings Volumes, 2006, 39(1): 714-716. DOI:10.3182/20060329-3-AU-2901.00111 |
| [15] |
罗华飞. MATLAB GUI设计学习手记[M]. 北京: 北京航空航天大学出版社, 2009. LUO H F. The design of learning notes of MATLAB GUI[M]. Beijing: Beihang University Press, 2009. |



