0 引言
随着世界能源消费的增长和石油勘探开发技术的不断提高,深水油气资源已经成为保障世界能源需求的重要领域。与陆上和浅海钻井相比,深水钻井面临着更多的挑战,如深水低温、窄安全密度窗口、浅层气和浅水流、易生成天然气水合物等。常规隔水管钻井井筒压力控制存在很大困难,导致溢流、漏失和井塌等井下复杂情况频发,难以应对这些深水难题[1-2]。研究表明,无隔水管钻井技术可有效控制深水窄密度窗口井筒压力,并能及时识别溢流,从而减轻浅层地质灾害的危害,工业应用前景广阔[3-5]。
无隔水管钻井时钻杆直接裸露于海水中,海面泵泵入的钻井液经地面管线、钻柱、钻头进入环空,从环空返回井口,经过吸入模块改变流向后进入海底举升泵,由海底举升泵将钻井液经返回管线举升回钻井平台。通过控制海底泵入口压力近似与海底处海水静压相当,模拟双梯度效应,可以有效控制海底泥线以下的井眼环空压力和井底压力,使地层孔隙压力和破裂压力之间狭小的间隙相对变宽[6],增加套管下深,降低钻井成本。
在海面泵排量较小、无隔水管钻进时,由于环空出口压力设定较低,只有降低钻杆内钻井液面高度才能实现井筒的压力平衡,此时钻杆顶部无法被钻井液充满[7]。当海面泵排量增大到某临界排量后[8-9],钻井液面到达钻杆入口,钻杆被钻井液充满,此时立压为零。当海面泵排量进一步增大、立压开始逐渐上升时,钻井液实现与传统钻井相同的连续循环。本文定义使钻杆充满钻井液所需的最小海面泵排量为零立压排量,以区别钻井液携岩所定义的临界排量。
对无隔水管钻井水力学的研究大多基于海面泵排量较大且使用钻柱阀的情况,从而保证钻柱内充满钻井液,无钻柱阀且海面泵排量较小时导致钻杆顶部不能充满钻井液工况的水力学分析则很少。目前只有葛瑞一[7]分析了无隔水管钻井钻柱未充满状态下的动液面计算方法。深水钻井具有海水低温和窄密度窗口的特点,对井底压力精确控制提出了更高的要求。关于无隔水管钻井在钻柱未充满工况下的井筒温度和压力模型还未见报道。针对这一问题,笔者首先给出了零立压排量、钻柱内平衡液面的计算方法,然后基于对稳态传热的等效类比建立了小排量工况下无隔水管钻井温度和ECD计算模型。研究结果对无隔水管钻井水力参数的确定具有一定的指导意义。
1 平衡液面深度与零立压排量 1.1 平衡液面深度 1.1.1 假设条件做如下基本假设:①钻柱与井筒同心;②钻井液不可压缩;③不考虑温度和压力对钻井液热物性参数的影响。
1.1.2 数学方程以海底为基准面,取平衡液面和海底环空出口两断面建立实际流体总流的伯努利方程:
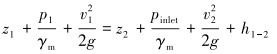
|
(1) |
式中:z1=Dw-h、z2=0分别为平衡液面高度和海底基准面,m;Dw、h分别为水深和未充满深度,m;p1、pinlet分别为钻杆入口和环空出口处的压力,MPa;v1、v2分别为钻杆入口和环空出口处的流速,m/s;γm为钻井液容重,N/m3;h1-2为水头损失,m;g为重力加速度,m/s2。
根据无隔水管钻井原理,保持吸入模块处入口压力为海底的海水静压,则有:
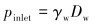
|
(2) |
式中:γw为水的容重,N/m3。
忽略流速水头的影响,对式(1)进行变形,可得:
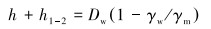
|
(3) |
由式(3)可知,当钻杆顶部未充满时,未充满深度h与循环系统水头损失h1-2之和保持不变。随着海面泵排量增大,h1-2增大,h减小,当排量足够大时,h减小为0,钻杆充满钻井液,此时立压从0开始增大,其计算式为:
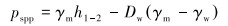
|
(4) |
对上式移项并令
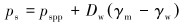
|
(5) |
则有:
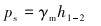
|
(6) |
式(6)与常规钻井立压计算式相同(不包括返回管线压耗),因此可定义ps为等效立压,显然实际立压小于等效立压。由式(5)可知,无隔水管钻井循环压耗不只由海面泵提供,钻柱内流体和泥线以下环空流体的静压差也为钻井液循环提供能量,这就是无隔水管钻井海面泵压远小于隔水管钻井泵压的原因。
1.2 零立压排量分析式(4)可知,当等式右边第二项足够大时,立压可减小为0,此时钻井液只在钻柱内和环空流体静压差作用下实现自流循环,海面泵只需提供平台管汇的流动压耗,海面泵排量即定义为零立压排量。令式(3)中h=0,得到零立压排量下水头损失满足的公式为:
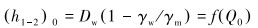
|
(7) |
对式(7)采用二分法即可得到零立压排量。
2 井筒温度和压力 2.1 温度模型无隔水管钻井在停泵后会发生U形管效应,钻井液继续流动,最后钻杆内平衡液面静止在新的位置。当重新开泵循环,井筒环空出口流量逐渐增大,经过一段时间后,注入排量与环空出口排量相等,井筒循环达到新的平衡,钻杆内平衡液面随注入排量的变化也会稳定在新的平衡位置。由于停泵发生U形管效应和重新注入过程的影响,所以将环境温度(海水和地层)作为井筒温度初始条件的已有温度计算模型(停泵后钻井液面下降,并不在循环位置恢复温度至与环境温度相同)。注入过程结束后,井筒和地层温度都已受到扰动,无法获知传统温度计算模型的初始条件。笔者认为可以假想这样一个模型,即认为注入后重新平衡的井筒钻井液在停泵后不会发生U形管效应,这样井筒温度在静止足够长的时间后可以恢复到与周围环境温度相同,在重新开泵循环后可以传统拟稳态温度计算模型计算传热稳定后的温度,该温度被认为是实际井筒注入钻井液后的稳定温度。基于以上模型假设,笔者采用C.S.KABIR等[10]提出的拟稳态传热模型研究了RMR钻井液未充满工况下传热稳定后的稳态温度场。
2.1.1 假设条件做如下基本假设:①井眼为圆形,钻柱处于与井眼同心的位置;②钻井液为单液相,不可压缩;③忽略钻井液轴向导热和钻井液的径向温度梯度,钻柱内和环空内的流体温度为一维分布;④钻井液和地层岩石的密度、比热容和导热系数与温度无关,为常数;⑤地层中仅有径向热传导;⑥不考虑压降生成热和机械生热。
2.1.2 数学模型对于海水段钻柱内钻井液,钻柱内微元控制体发生的热量传递过程有z方向钻井液流动携带的热量和r方向与钻柱内壁面径向对流换热。根据热力学第一定律,得到钻柱内温度控制方程为:
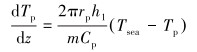
|
(8) |
返回管线内微元控制体发生的热量传递过程有z方向钻井液流动携带的热量和r方向与返回管线内壁面径向对流换热。则返回管线内温度控制方程为:
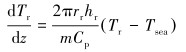
|
(9) |
对于地层段钻柱内微元控制体,可得到:
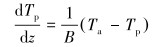
|
(10) |
其中,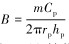
对于环空钻井液,环空内微元控制体发生的热量传热过程为z方向钻井液流动携带的热量和r方向与钻柱外壁面及井壁(或套管壁)径向对流换热,从而得到环空内温度控制方程如下。
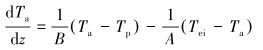
|
(11) |
其中,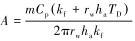
A与无因次时间TD有关,TD的经验公式为[10]:
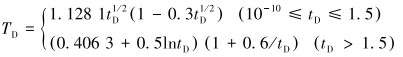
|
(12) |
其中,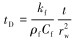
式中:Tp、Ta、Tei、Tr和Tsea分别为钻柱内流体温度、环空流体温度、井壁温度、返回管线内流体温度和海水温度,℃;rp、rr和rw分别为钻柱内径、返回管线内径和井眼半径,m;h1、hp、hr、ha分别为海水段钻杆内流体与海水的总换热系数、地层段钻杆内流体与环空流体总换热系数、海水段返回管线内流体与海水的总换热系数、井壁或套管内壁换热系数,W/(m2·℃);m为质量流量,kg/s;Cp、Cf分别为钻井液的比热容和地层的比热容,J/(kg·℃);ρf为地层密度,kg/m3;kf为地层导热系数,W/(m·℃);z为深度坐标,m;t为循环时间,s。
2.1.3 初边值条件钻柱入口温度可在钻井平台测量,但小排量下平衡液面不在钻柱入口,因此当平衡液面深度在小于200 m的海水混合层和温跃层时,需要对平衡液面温度进行测量。对于深度大于200 m的恒温层,由于海水温度变化很小,可以假设平衡液面温度为该深度处海水温度。钻柱和环空在井底相连通,所以钻柱内钻井液和环空钻井液在井底温度应相等,即有:
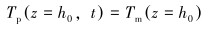
|
(13) |
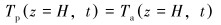
|
(14) |
式中:h0为平衡液面深度,m;Tm为平衡液面的温度,℃。
2.1.4 模型计算海水段钻杆和返回管线内钻井液温度模型需数值求解,离散方程为:
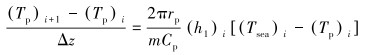
|
(15) |
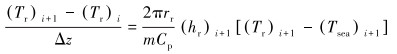
|
(16) |
地层段钻杆内和环空钻井液温度的解析解为:
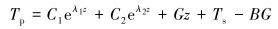
|
(17) |
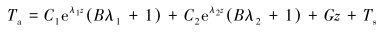
|
(18) |
其中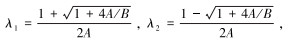
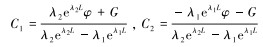
式中:L为泥线下井深,m。
2.2 钻井液当量循环密度预测模型以向下为正方向,连续性方程可统一为:
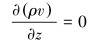
|
(19) |
动量方程为:
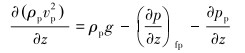
|
(20) |

|
(21) |
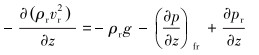
|
(22) |
式中:ρp、ρa、ρr分别为钻杆内、环空和返回管线内钻井液密度,kg/m3;vp、va、vr分别为钻杆内、环空和返回管线内钻井液流速,m/s;pp、pa、pr分别为钻杆内、环空和返回管线内钻井液压力,MPa;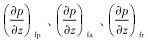
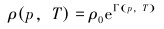
|
(23) |
其中
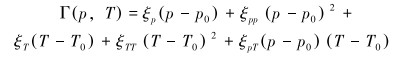
|
(24) |
式中:p0和T0分别是地面压力和温度;ξp、ξT、ξpp、ξTT、ξpT是模型回归系数,不同的钻井液系数不同。
无隔水管(RMR)钻井循环系统循环压降计算方法见文献[15]。
3 实例分析某深水井水深3 000 m,井深9 000 m,水基钻井液密度1 640.1 kg/m3,海水密度1 030 kg/m3,钻井液比热容和热导率分别为2 439.9 J/(kg·℃)和1.73 W/(m·℃),地层密度、比热容和热导率分别为2 675 kg/m3、837.3 J/(kg·℃)和2.419 W/(m·℃)。钻井液为幂律流体,其稠度系数为0.34,流性指数为0.65。钻头直径为216 mm,钻杆外径为127 mm,返回管线外径为152 mm,海面温度为27 ℃,海面泵排为15.4 L/s,对应的平衡液面位置位于海面以下500 m,海水温度分布见文献[12, 16]。钻井液密度预测公式采用E.KARSTAD[14]根据试验数据回归的模型。
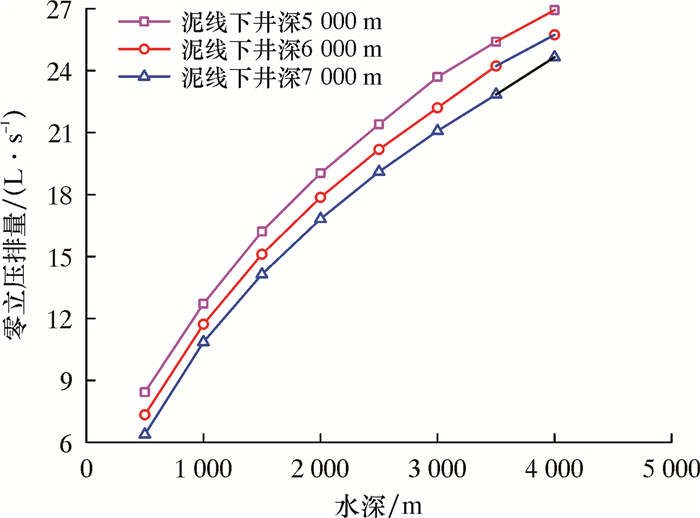
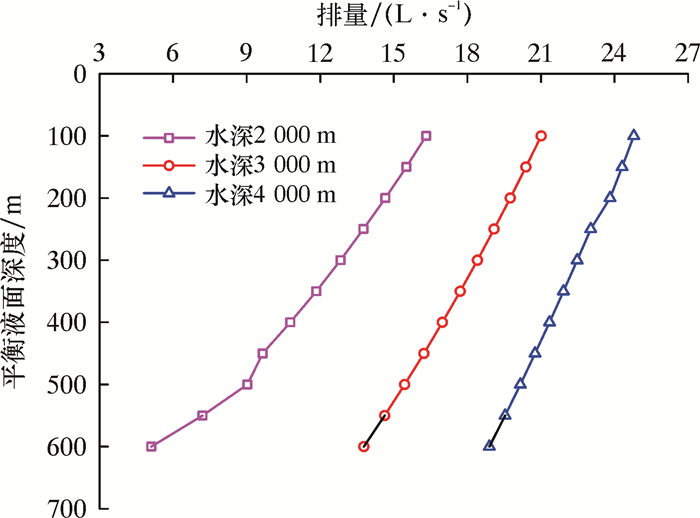
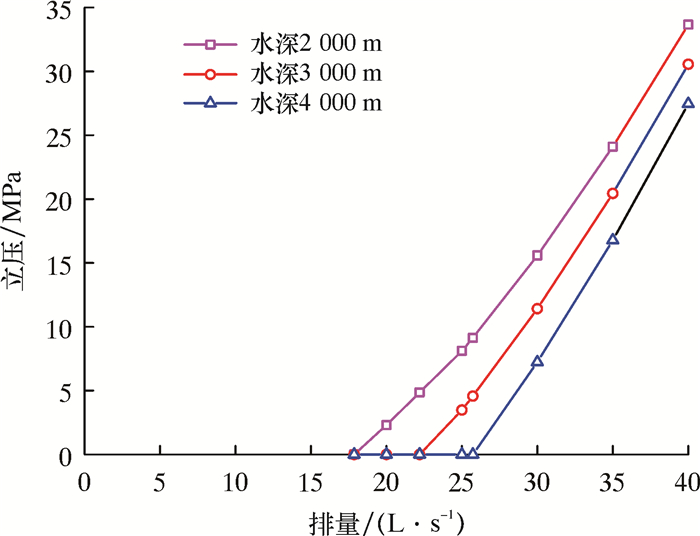
图 1是零立压排量与水深的的关系曲线。由图 1可知,零立压排量均随着水深的增加而增加,随着井深的增加而减小。图 2是平衡液面深度与排量的关系曲线。从图 2可知:排量越大,平衡液面位置距平台越近;水深越大,相同排量下的平衡液面深度距平台越远。图 3是立压与排量的关系曲线。由图 3可见:当排量较小时钻柱没有充满钻井液,因此立压为0;当排量增大到超过零立压排量时,立压随排量增大而增大,随水深增大而减小。
|
| 图 1 零立压排量随水深的变化曲线 Fig.1 Zero standpipe pressure displacement versus water depth |
|
| 图 2 平衡液面深度随排量的变化曲线 Fig.2 Equilibrium liquid level depth versus displacement |
|
| 图 3 立压随排量的变化曲线 Fig.3 Standpipe pressure versus displacement |
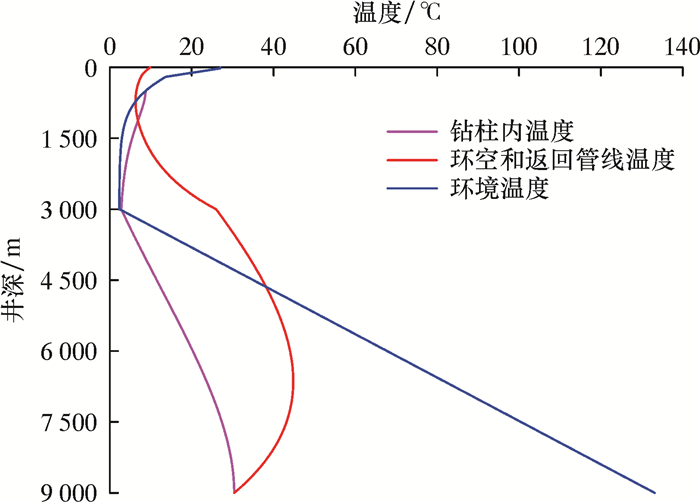
图 4是RMR钻井传热8 h后的稳定温度曲线。
|
| 图 4 温度随井深的变化曲线 Fig.4 Temperature versus well depth |
由图 4可知,平衡液面位置为500 m时,海水段钻杆内的温度与环境温度接近,海底处钻杆内钻井液温度为2.8 ℃,地层段钻杆内温度随井深增加而升高,环空温度则先升高后降低,地层段井筒温度的变化规律与陆上井相同。环空内钻井液温度高于钻杆内温度,钻杆内温度最高值位于井底,为30.4 ℃,环空最高温度为44.8 ℃,该处井深为6 640 m,地层段井筒温度都远低于原始地层温度,即RMR深水钻井井筒温度变化比陆上钻井小很多。返回管线内钻井液温度随水深先降低后升高,在海底处温度为26.0 ℃,最低温度为6.3 ℃,出口温度为9.9 ℃。
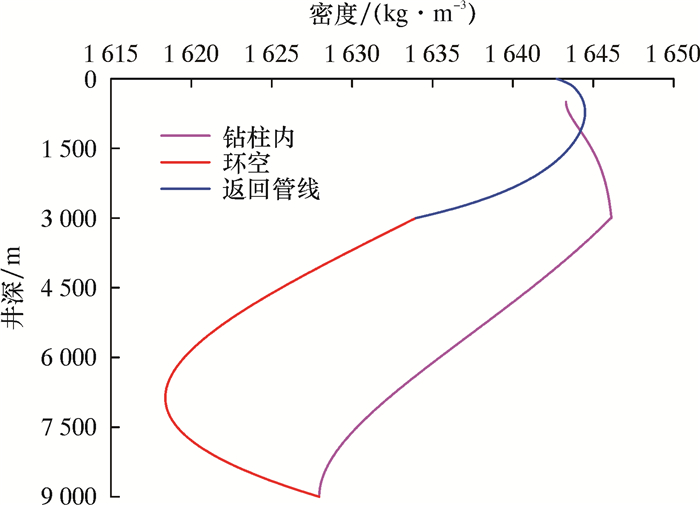
图 5是RMR钻井井筒钻井液密度分布曲线。由于海水低温,海水段钻杆内钻井液温度逐渐降低,又因为温度对钻井液密度的影响远大于压力,所以钻井液密度从平衡液面位置到海底一直增大。地层段钻杆内钻井液温度逐渐升高,因而密度一直减小。因为从井底到海底,环空温度先升高后降低,所以钻井液密度先减小后增大。对于返回管线,从海底到平台,返回管线的温度先升高后降低,因此钻井液密度先增大后减小。
|
| 图 5 钻井液密度变化曲线 Fig.5 Drilling fluid density variation |
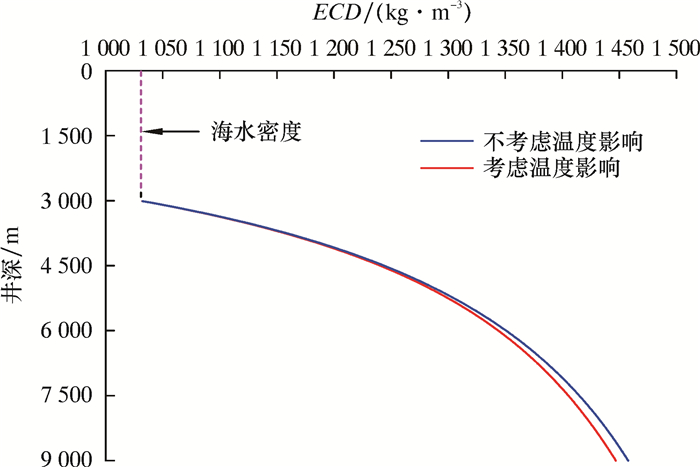
图 6是ECD分布曲线。由图 6可知,ECD随井深增加而增大,考虑温度影响的ECD比不考虑温度影响的ECD要小10.8 kg/m3。对于深水高温高压井,由于窄密度窗口的特点,井底压力和ECD的计算需要考虑温度的影响,否则容易出现溢流和漏失等井下复杂情况,但总体而言,由于深水井筒温度受水下井口入口低温的影响,导致温度变化比陆上井筒温度要小,所以井底压力和ECD变化也相应要小。
|
| 图 6 ECD分布曲线 Fig.6 ECD distribution |
4 结论
(1) 无隔水管钻井存在零立压排量,若海面泵排量小于该排量,则钻柱顶部无法被钻井液充满,此时海面平台立压为零。零立压排量随水深增加而增加,随井深增加而减小。
(2) 无隔水管钻井的循环压耗(不包括返回管线)由等效立压决定。实际立压小于等效立压,水深越深,钻井液密度越大,实际立压越小。这就是无隔水管钻井立压比常规隔水管钻井立压小得多的原因。当海面泵排量大于零立压排量时,立压随排量增大而增大,随水深增大而减小。
(3) 当海面泵排量小于零立压排量时,平衡液面处于海水中。排量越大,平衡液面位置距平台越近。水深越大,相同排量下的平衡液面深度距平台越远。
(4) 海水段钻杆内钻井液温度随水深增加而降低,返回管线温度随水深增加先降低后升高,地层段井筒温度变化规律与陆上井筒温度变化规律一致,但温度要低很多。
(5) 由于无隔水管钻井井筒温度变化不大,所以井底压力和ECD变化也较小。但由于温度对钻井液流变性影响很大,特别是海水低温段的钻井液流变参数变化规律研究的较少,所以应加强深水钻井低温高压环境下钻井液流变性的研究。
| [1] |
罗洪斌, 田波, 蒋世全, 等. 考虑海底增压的深水钻井当量循环密度预测方法[J]. 石油钻采工艺, 2015, 37(1): 72-75. LUO H B, TIAN B, JIANG S Q, et al. Prediction method for equivalent circulating density of deepwater drilling when subsea pressurization is considered[J]. Oil Drilling & Production Technology, 2015, 37(1): 72-75. |
| [2] |
郝希宁, 蒋世全, 孙丽丽, 等. 深水钻井当量循环密度影响规律分析[J]. 石油钻采工艺, 2015, 37(6): 49-52. HAO X N, JIANG S Q, SUN L L, et al. Analysis on influence law of equivalent circulating density in deepwater drilling[J]. Oil Drilling & Production Technology, 2015, 37(6): 49-52. |
| [3] |
彭齐, 樊洪海, 纪荣艺, 等. 无隔水管钻井浅部地层井筒循环压耗分析[J]. 石油机械, 2015, 43(8): 73-77. PENG Q, FAN H H, JI R Y, et al. Analysis of circulating pressure drop in surface formation wellbore in riserless drilling[J]. China Petroleum Machinery, 2015, 43(8): 73-77. |
| [4] |
周昌静, 陈国明, 刘杰, 等. 无隔水管钻井泥浆举升系统参数计算[J]. 石油钻采工艺, 2011, 33(1): 42-44. ZHOU C J, CHEN G M, LIU J, et al. Parametric computation of mud lift system in riserless drilling[J]. Oil Drilling & Production Technology, 2011, 33(1): 42-44. DOI:10.3969/j.issn.1000-7393.2011.01.012 |
| [5] |
刘杰, 陈国明, 周昌静, 等. 深水无隔水管钻井液回收钻井水力学计算[J]. 石油钻采工艺, 2010, 32(5): 20-23. LIU J, CHEN G M, ZHOU C J, et al. Hydraulics calculation of deepwater riserless mud recovery drilling[J]. Oil Drilling & Production Technology, 2010, 32(5): 20-23. DOI:10.3969/j.issn.1000-7393.2010.05.005 |
| [6] |
刘杰.无隔水管泥浆返回钻井系统水力学计算及吸入模块设计[D].青岛: 中国石油大学(华东), 2010. LIU J. Hydraulics calculation and suction module design for riserless mud recovery drilling system[D]. Qingdao: China University of Petroleum(Huadong), 2010. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1709130 |
| [7] |
葛瑞一.无隔水管钻井泥浆举升系统设计与控制单元研究[D].青岛: 中国石油大学(华东), 2013. GE R Y. Study on riserless mud-lift drilling system design and control unit[D]. Qingdao: China University of Petroleum(Huadong), 2013. http://cdmd.cnki.com.cn/Article/CDMD-10425-1015025475.htm |
| [8] |
彭齐, 樊洪海, 纪荣艺, 等. 无隔水管钻井技术临界排量分析[J]. 石油机械, 2016, 44(2): 48-52. PENG Q, FAN H H, JI R Y, et al. Analysis on the critical displacement of riserless drilling technology[J]. China Petroleum Machinery, 2016, 44(2): 48-52. |
| [9] |
CHOE J. Analysis of riserless drilling and well-control hydraulics[J]. SPE Drilling and Completion, 1999, 14(1): 71-81. DOI:10.2118/55056-PA |
| [10] |
KABIR C S, HASAN A R. Determining circulating fluid temperature in drilling, workover, and well control operations[J]. SPE Drilling & Completion, 1996, 11(2): 74-79. |
| [11] |
宁立伟.钻井液物性参数对深水钻井井筒温度压力的影响[D].青岛: 中国石油大学(华东), 2008. NING L W. The effect of drilling fluid's physical properties on the temperature and pressure in deepwater drilling[D]. Qingdao: China University of Petroleum(Huadong), 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1363155 |
| [12] |
王博.深水钻井环境下的井筒温度压力计算方法研究[D].青岛: 中国石油大学(华东), 2007. WANG B. Research on the method of wellbore temperature and pressure calculation during deep-water drilling[D]. Qingdao: China University of Petroleum(Huadong), 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1214396 |
| [13] |
王利国.高温深井钻井液当量循环密度预测模型及影响因素分析[D].北京: 中国石油大学(北京), 2008. WANG L G. Study on prediction model and analysis on influence factors of equivalent circulating density of drilling fluid under conditions of high-temperature deep wells[D]. Beijing: China University of Petroleum(Beijing), 2008. http://d.wanfangdata.com.cn/Periodical/zjyywjy200902009 |
| [14] |
KARSTAD E, AADNOY B S. Density behavior of drilling fluids during high pressure high temperature drilling operations[C]//IADC/SPE Asia Pacific Drilling Technology.[S.l.]: Society of Petroleum Engineers, 1998.
|
| [15] |
樊洪海. 实用钻井流体力学[M]. 北京: 石油工业出版社, 2014. FAN H H. Practical drilling fluid mechanics[M]. Beijing: Petroleum Industry Press, 2014. |
| [16] |
高永海, 孙宝江, 王志远, 等. 深水钻探井筒温度场的计算与分析[J]. 中国石油大学学报(自然科学版), 2008, 32(2): 58-62. GAO Y H, SUN B J, WANG Z Y, et al. Calculation and analysis of wellbore temperature field in deepwater drilling[J]. Journal of China University of Petroleum(Edition of Natural Science), 2008, 32(2): 58-62. DOI:10.3321/j.issn:1673-5005.2008.02.012 |


