2. 湖北省油气钻完井工具工程技术研究中心;
3. 非常规油气湖北省协同创新中心;
4. 中石化石油机械股份有限公司第四机械厂
2. Oil and Gas Drilling and Well Completion Tools Research Center of Hubei Province;
3. Hubei Cooperative Innovation Center of Unconventional Oil and Gas;
4. SJ Petroleum Machinery Co., SINOPEC
0 引言
齿轮齿条在实际应用过程中,由于制造工艺、安装方法、工作载荷和外部干预等原因,可能会发生弯曲变形,导致其传动特性发生变化,所以需要对弯曲齿条的传动性能进行研究。
国内外学者对齿轮齿条弯曲现象进行了大量研究。阳培等[1]致力于提高齿轮齿条弯曲强度的方法研究;李永祥等[2]结合工程实际提出了大模数齿轮齿条弯曲疲劳强度试验的研究思路;叶福民等[3]对齿轮齿条模型进行接触分析,分析了压力角和模数对接触应力与弯曲应力的影响;刘伟[4]通过有限元分析与试验对比研究, 搭建了齿条的弯曲模型;J.MAJTENYI等[5]研究了齿条残余应力状态与宏观变形,证明淬火温度对构件变形没有影响,而应力不对称是杆件弯曲的原因;G.K.TRIANTAFYLLIDIS等[6]研究了齿条转向器弯曲失效机理,发现脱氧措施和硬涂层缺陷会导致弯曲塑性变形。
本文结合实际应用情况,对齿条弯曲现象[7-8]进行分析,分别通过有限元方法与几何方法验证弯曲齿条对齿轮齿条传动的影响,并从重合度与齿廓干涉两个方向判断齿条弯曲对其传动性能的影响,以期为弯曲情况下齿条的传动研究提供理论参考。
1 有限元分析以某种型号的齿轮齿条钻机为对研究对象,对一段与齿轮啮合传动的齿条(长1 900 mm)施加载荷,齿条沿齿侧弯曲发生变形。用ANSYS对其进行有限元分析。齿轮齿条相关参数如表 1所示。
| 参数名称 | 齿轮 | 齿条 |
| 模数/mm | 25 | 25 |
| 齿数 | 12 | — |
| 压力角/(°) | 20 | 20 |
| 齿顶高系数 | 1 | 1 |
| 顶隙系数 | 0.25 | 0.25 |
| 齿宽/mm | 180 | 160 |
| 分度圆直径/mm | 300 | — |
| 变位系数 | 0.5 | — |
齿轮材料为20CrMnTi,经过调质-气体渗氮处理为渗氮钢,齿条材料为40Cr。
由于齿轮齿条形状相对不规则,对齿轮齿条线接触部分进行局部加密,故网格比例系数取1,实体单元最大单元尺寸为20 mm,接触部分最大单元尺寸为1 mm,共划分实体单元71 412个。齿轮齿条线接触模型网格划分见图 1。经网格质量检查,单元尺寸比较均匀,满足工程计算需求。

|
| 图 1 齿轮齿条网格划分示意图 Fig.1 Schematic diagram of meshing of rack and pinion |
据该型号齿轮齿条钻机钩载要求,对单个齿轮施加45.94 kN·m扭矩,对齿条顶部施加9 kN·m弯矩作为迫使齿条向齿侧弯曲的载荷。
对齿条底面施加固定约束、齿轮施加铰约束,只能实现沿齿轮中心轴线的转动,施加46 kN·m的扭矩,齿条顶部施加9 kN·m弯矩。齿轮齿条载荷与约束情况如图 2所示。
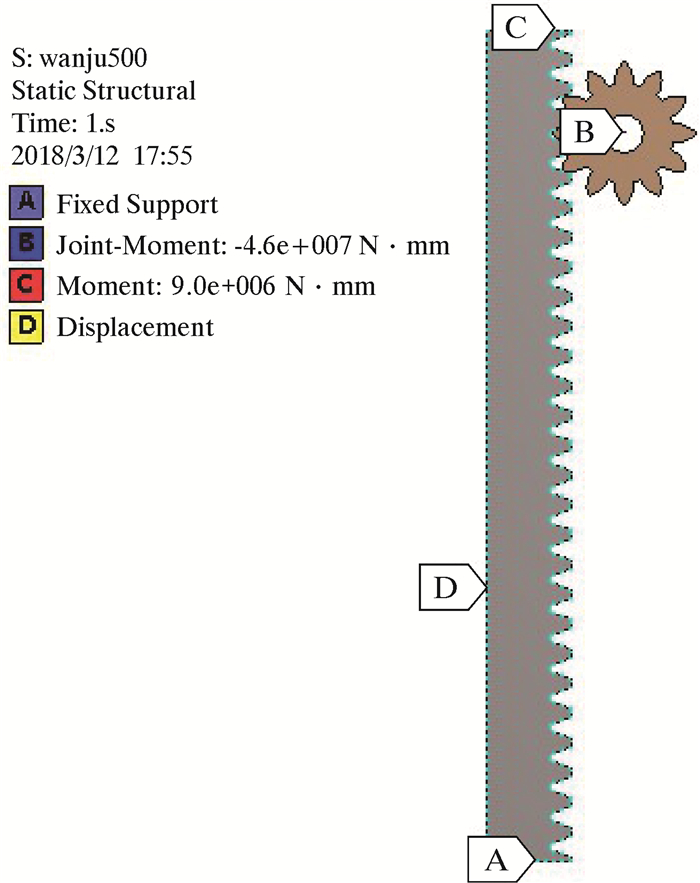
|
| 图 2 齿轮齿条施加载荷示意图 Fig.2 Schematic diagram of the loads applied on the rack and pinion |
图 3为齿轮的Von Mises应力云图。从图 3可以看出,其等效应力集中在齿轮根部且在齿条弯曲方向上逐渐增大,最大应力为1 187.7 MPa。

|
| 图 3 齿轮的Von Mises应力云图 Fig.3 The Von Mises stress distribution of the gear |
齿条的变形云图如图 4所示。从图 4可以看出,齿条与齿轮接触部位存在一定程度的变形,最大变形量为0.750 2 mm。
|
| 图 4 齿条的变形云图 Fig.4 Deformation of the rack |
由有限元分析结果可知,当齿条受侧面载荷沿侧面弯曲时,即便变形量极小,齿轮也会产生较大的集中应力,对轮齿的危害极大,导致齿轮齿条传动性能降低。为避免这种情况发生,需要计算齿条沿齿侧端所允许的最大变形。
2 齿条齿侧变形几何分析由于齿条发生弯曲后两端齿侧变形对齿轮齿条啮合有不同的影响[9-11],故需要分别对两侧的啮合条件进行讨论。为得到弯曲后齿条最大允许变形,以下主要以一段齿条弯曲量最大处啮合的一对轮齿作为分析对象。对一段齿条建立空间直角坐标系,结果如图 5所示。
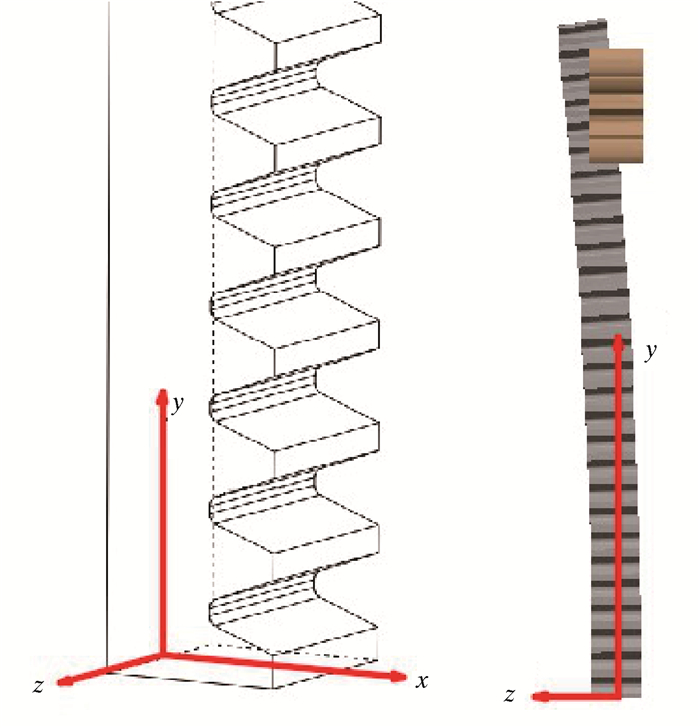
|
| 图 5 齿条坐标系示意图 Fig.5 Schematic diagram of the rack coordinate system |
建立齿条沿齿侧方向的弯曲模型,做如下假设。
(1) 齿条仅在齿侧方向发生微量弯曲变形,变形后齿条近似为圆弧段,对齿条的传动分析建立在齿轮齿条保持连续传动的基础上。
(2) 当齿条绕x轴顺时针方向弯曲时,齿条弯曲方向一端齿侧发生挤压变形,另一端发生拉伸变形。假设齿条发生变形时,轮齿的齿形不发生改变,变形集中在齿槽位置。
(3) 齿条齿侧截面中心面处的齿条弯曲不改变其齿距长度,齿条弯曲方向一端齿侧齿间距减小,另一端齿侧齿间距增大。
(4) 齿条的弯曲变形不改变其他的齿条特性。
综合考虑齿条弯曲后两齿侧的变形情况,分别从重合度和轮廓干涉角度,对齿条最大允许变形进行讨论。设一个齿间距齿条弯曲角度为σ,如图 6所示。根据假设(3),齿条中心面处齿间距为P,齿条弯曲方向的齿侧端齿间距为P1,与齿条弯曲方向相反的齿侧端齿间距为P2。

|
| 图 6 齿条弯曲后齿间距变化示意图 Fig.6 Schematic diagram of the change of tooth spacing after bending of the rack |
2.1 齿条弯曲方向的齿侧端分析
设此端面齿间距减小Δl1,即齿距为:
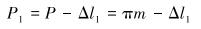
|
(1) |
依据图 6可得:

|
(2) |
式中:b为齿条齿宽,mm;m为齿条模数,mm。
此时齿条分度线发生偏转,设偏转距离为Δx,则有:
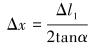
|
(3) |
式中:α为压力角,(°)。
变位系数为x的齿轮齿条传动重合度为:
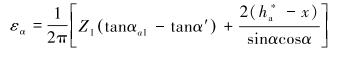
|
(4) |
式中:ha*为齿顶高系数。
当齿条发生偏移即非标准安装时,重合度为:

|
(5) |
将重合度作为衡量齿轮副传动平稳性及传递载荷稳定性的重要指标,齿条弯曲后要求重合度应不小于许用重合度,即:

|
(6) |
设此端面齿间距增加Δl2,即齿距为:

|
(7) |
依据图 6可得:
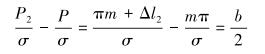
|
(8) |
齿轮正常传动的条件是:当齿轮齿条的一对齿完全啮合后,齿条齿间距的增加不会使下一个齿条轮齿的齿尖碰触齿轮下一个轮齿。设未发生弯曲时,当齿轮齿条的一对齿完全啮合后,齿条轮齿的齿尖在传动方向(齿条分度线方向)距碰触齿轮下一个轮齿距离为s,即要求:
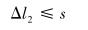
|
(9) |
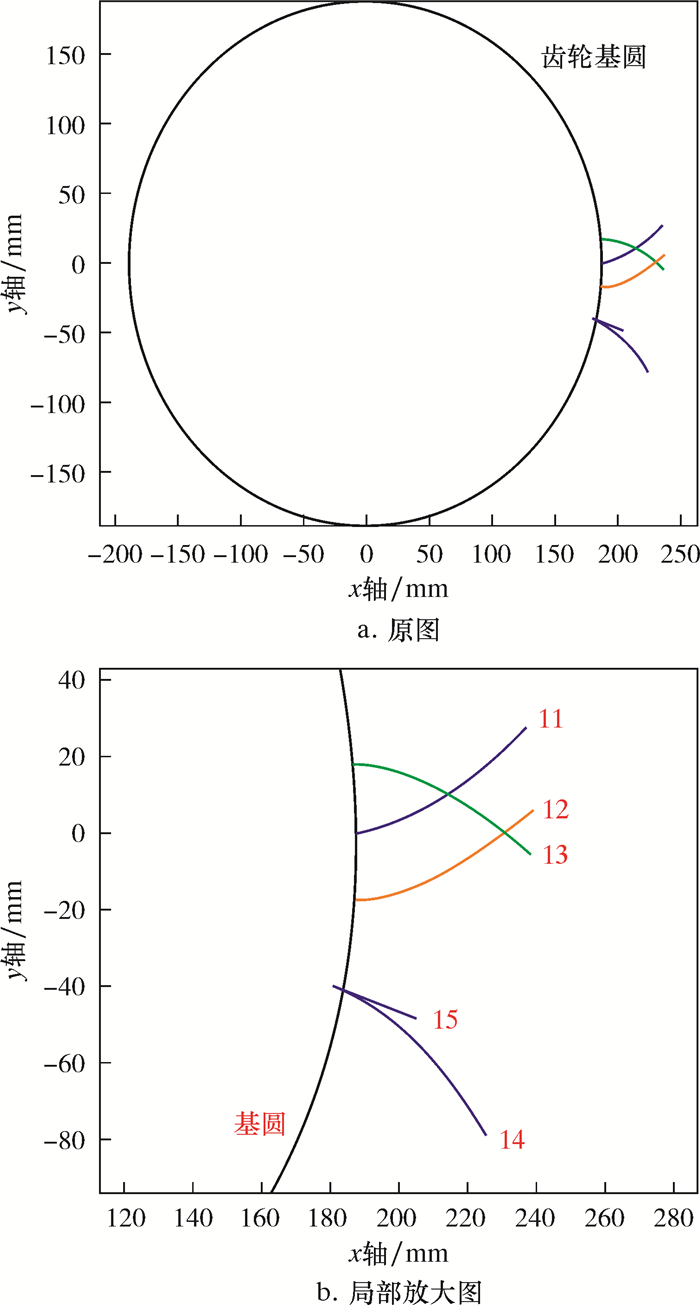
齿轮齿廓渐开线坐标图如图 7所示。由图可知,l1为基圆半径r的标准渐开线,以基圆圆心为原点建立直角坐标系,渐开线起点在x正轴上,则曲线的参数方程为:

|
(10) |
|
| 图 7 轮齿轮廓渐开线坐标图及其局部放大图 Fig.7 Involute curve of the tooth profile and its partial enlargement |
式中:φ为曲线上任意一点对基圆切线的切点对应的半径线与x轴的夹角,(°)。
为方便计算,准确求出齿轮齿廓的参数方程,对l1进行坐标系转换。以基圆圆心为原点,y轴平行于齿条分度线建立直角坐标系,即将l1对应坐标系逆时针旋转δ角度,得到齿轮轮齿轮廓线l2,其曲线方程为:
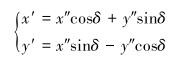
|
(11) |
式中:δ为半个轮齿对应的圆心角,即单个轮齿一侧渐开线起点到轮齿中心线所对应齿廓的圆心角。
将l2对x轴镜像,得到另一侧齿廓线l3,其曲线方程为:
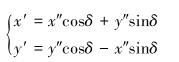
|
(12) |
l4为齿轮下一个齿的轮廓线,其曲线方程为:
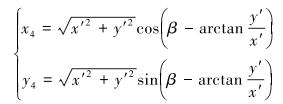
|
(13) |
式中:β为齿轮一个齿间距对应的夹角,(°)。
则有:
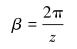
|
(14) |
式中:z为齿轮齿数。
l5为齿条中最靠近l4的轮齿轮廓线,其曲线方程为:
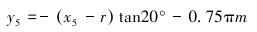
|
(15) |
式中:r为齿轮分度圆半径。
设s=min {| y4-y5| },即s为l4与l5间最小距离,则要求:
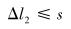
|
(16) |
对于与齿条弯曲方向相反的齿侧端,若要齿轮齿条能够平稳连续传动,则齿条在一个齿距的范围内齿轮齿间距增加不应超过s。
通过对齿条齿间距改变量进行约束,结合图 6的几何关系,可以对齿条弯曲角度σ进行限制,得到弯曲角度σ的最大允许量。根据假设(1),齿条弯曲后近似圆弧,通过几何运算可计算出齿条顶端最大变形量。
3 实例分析以上述齿轮齿条钻机为例,对其齿条齿侧变形进行几何分析。
3.1 齿条弯曲方向的齿侧端分析齿轮分度圆半径为:
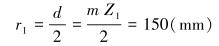
|
(17) |
式中:d为分度圆直径,mm。
齿顶圆半径为分度圆半径加上齿顶高,即:
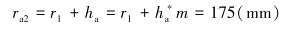
|
(18) |
式中:ha为齿顶高,mm。
齿轮基圆半径:
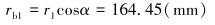
|
(19) |
则有齿顶压力角:
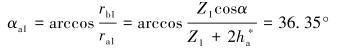
|
(20) |
设许用重合度[εα]=1.4,则有:
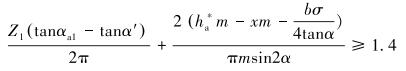
|
(21) |
其中齿条齿宽b=160 mm,解得σ≤0.992°
3.2 与齿条弯曲方向相反的齿侧端分析通过MATLAB求解可得:
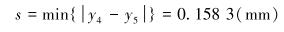
|
(22) |
则有:
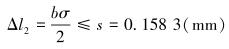
|
(23) |
解得:
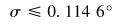
|
(24) |
综上所述可知,齿条弯曲角度φ应满足如下条件:
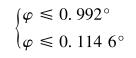
|
(25) |
即弯曲角度φ应小于0.114 6°。
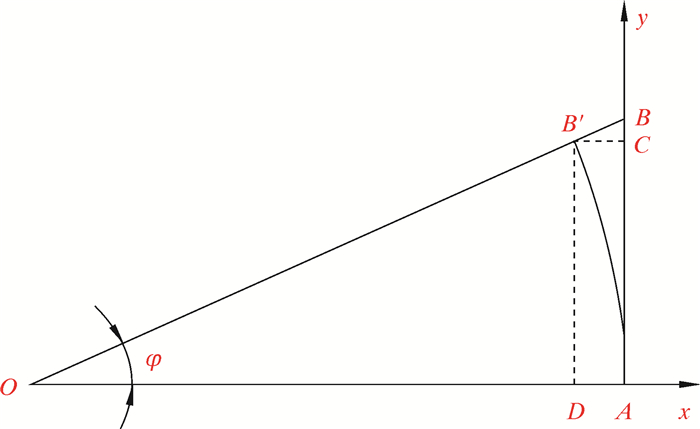
如图 8所示,长度为L的AB段齿条发生弯曲,弯曲角度为φ,弯曲后齿条为圆弧段AB′,则齿条最大变形量为BB′。
|
| 图 8 齿条弯曲示意图 Fig.8 Schematic diagram of the bending of the rack |
已知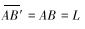
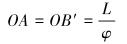
|
(26) |
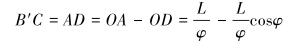
|
(27) |
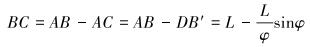
|
(28) |
最后可得:
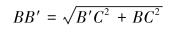
|
(29) |
通过上述计算可知:无论是齿条弯曲方向齿侧端还是与齿条弯曲方向相反齿侧端,齿宽越大,齿条弯曲角度φ越小;而对于发生弯曲的齿条,其长度越长,齿条最大变形量BB′越大。
4 结论(1) 当齿条沿齿侧方向弯曲时,在齿轮传动过程中,在齿轮齿根处会发生应力集中现象,影响齿轮齿条正常传动。因此,应尽量减小齿侧方向的载荷,当齿条齿侧受弯矩而弯曲时,即使齿条变形微小,也会对齿轮造成极大损伤,缩短齿轮使用寿命,甚至损毁齿轮。
(2) 提出以重合度与轮廓干涉作为判定弯曲后齿条能否正常传动的依据。齿条沿齿侧方向弯曲后,齿条弯曲方向齿侧齿间距减小,重合度随之降低,要求重合度满足许用值;对于与弯曲方向相反齿侧端,要求齿间距增加后,齿轮传动到下一轮齿时不发生干涉。
(3) 结合实际应用,以齿轮齿条钻机一段齿条为例,得到其最大允许弯曲角度,并推出最大变形量计算公式,得到齿条齿宽、齿条长度对最大允许变形的影响。对于长齿条,建议加大齿条齿宽,并采取分节安装等措施来避免齿条弯曲长度过大。
| [1] |
阳培, 刘忠明, 王长路. 大模数齿轮齿条承载能力影响因素分析[J]. 机械传动, 2009, 33(5): 27-31. YANG P, LIU Z M, WANG C L. Analysis of influencing factors on load-bearing capacity of large modulus gear and rack[J]. Journal of Mechanical Transmission, 2009, 33(5): 27-31. DOI:10.3969/j.issn.1004-2539.2009.05.010 |
| [2] |
李永祥, 王振, 王明旭, 等. 大模数齿轮齿条弯曲疲劳强度的探讨[J]. 机械传动, 2012, 36(10): 1-3. LI Y X, WANG Z, WANG M X, et al. Discussion of large modulus gear-rack bending fatigue strength[J]. Journal of Mechanical Transmission, 2012, 36(10): 1-3. |
| [3] |
叶福民, 孟淼. 自升式海洋平台齿轮齿条接触强度分析[J]. 计算机仿真, 2017, 34(11): 280-284. YE F M, MENG M. Analysis of contact strength of gear and rack in self elevating offshore platform[J]. Computer Simulation, 2017, 34(11): 280-284. DOI:10.3969/j.issn.1006-9348.2017.11.061 |
| [4] |
刘伟. 基于有限元的齿条弯曲分析及优化应用[J]. 机械工程与自动化, 2018(3): 43-45. LIU W. Bending analysis and optimization applications of racks based on finite element method[J]. Mechanical Engineering & Automation, 2018(3): 43-45. DOI:10.3969/j.issn.1672-6413.2018.03.016 |
| [5] |
MAJTENYI J, BENKE M, MERTINGER V, et al. The effect of quenching temperature and polishing force on the residual stress and deformation of rack bar semi-products[J]. Materials Science Forum, 2017, 885: 1-6. DOI:10.4028/www.scientific.net/MSF.885 |
| [6] |
TRIANTAFYLLIDIS G K, ANTONIOU A S. Investigation of the failure mechanism by bending of a rack steering gear[J]. Journal of Failure Analysis & Prevention, 2011, 11(4): 379-384. |
| [7] |
冯定, 亢博文, 施雷, 等. 大模数重载齿轮齿条接触强度分析[J]. 石油机械, 2018, 46(8): 14-19. FENG D, KANG B W, SHI L, et al. Analysis of contact strength of large module heavy load rack and pinion[J]. China Petroleum Machinery, 2018, 46(8): 14-19. |
| [8] |
蔡俊.齿轮齿条钻机系统动力学研究[D].荆州: 长江大学, 2016. CAI J. A dynamics research of rack and pinion drill rig system[D]. Jingzhou: Yangtze University, 2016. |
| [9] |
冯定, 杨行, 冯一璟, 等. 基于Matlab的渐开线少齿差行星齿轮变位系数取值方法研究[J]. 机械传动, 2017, 41(7): 18-21. FENG D, YANG H, FENG Y J., et al. Research of the method of selection of modification coefficient value of the planetary involute gear[J]. Journal of Mechanical Transmission, 2017, 41(7): 18-21. |
| [10] |
MARANO D, PIANTONI A, TABAGLIO L, et al. Effects of gear manufacturing errors on rack and pinion steering meshing[C]//First World Congress on Condition Monitoring, London, June 2017.
|
| [11] |
李春生. 交流变频电动顶驱系统下齿轮箱体的结构优化[J]. 石油机械, 2017, 45(8): 26-30. LI C S. Structure Optimization of lower gear box of ac variable frequency electric top drive system[J]. China Petroleum Machinery, 2017, 45(8): 26-30. |


