0 引言
在当前的石油行业中,钻井作业已经由浅井向深井、超深井及深海井进军。涡轮钻具作为常用井下动力钻具中的一种,以其独特的特点在钻井现场得到了广泛应用[1-2]。叶栅是整个涡轮钻具重要的组成部分,而涡轮叶片的水力性能直接影响涡轮叶栅的性能,归根结底,涡轮叶栅的核心部件便是涡轮叶片。要想进一步提升涡轮钻具的效率和使用的稳定性,就需要设计具有更高性能的涡轮叶片[1]。
涡轮叶片的参数调控优化设计能够较好地改善涡轮钻具的转矩、效率等水力性能,因此对涡轮叶栅叶片的参数进行分析、设计和优化具有一定的工程实际意义。笔者基于贝塞尔曲线理论和流体动力学理论,通过理论分析、仿真模拟及试验对比等方法全面研究了涡轮叶片参数设计对涡轮叶片性能的影响[2-3],以期为高性能涡轮叶片型线的设计提供参考。
1 涡轮叶栅及叶片设计 1.1 贝塞尔曲线参数化造型贝塞尔曲线理论于20世纪90年代已经形成,由于其在几何设计及外观造型方面有着易控制及设计方便等优势,被广泛应用于汽车、航空及轮船等领域[4]。贝塞尔曲线根据特征多边形的控制点来定义,通过在起始点和终点之间构造多项式函数,即给定空间k+1个控制点Pi(i=0, 1, 2, …, k),这些控制点就组成k阶贝塞尔曲线特征多边形[3],此时的曲线可以表示为:
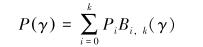
|
(1) |
式(1)中参数γ的取值为[0, 1],Bi, k(γ)为k次古典伯恩斯坦(Berstein)基函数,即插补函数。
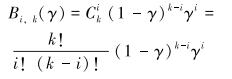
|
(2) |
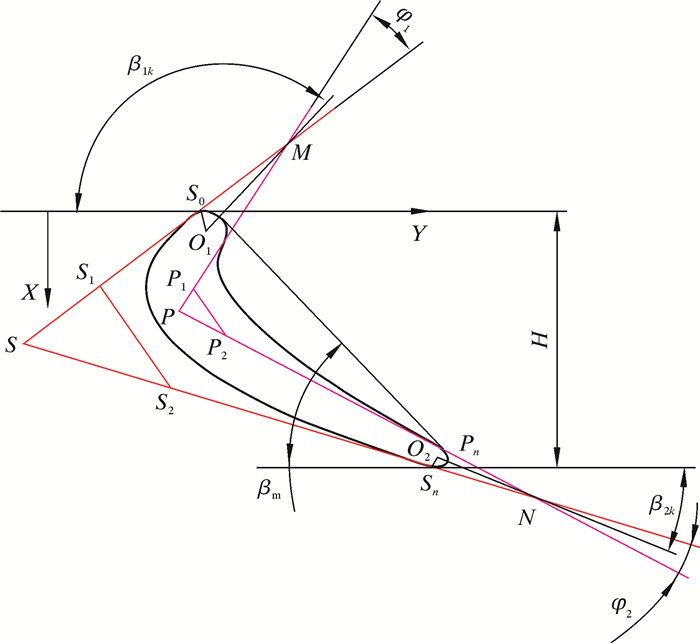
通常在工程实际中,贝塞尔曲线多数采用的是二次和三次贝塞尔曲线。其中三次贝塞尔曲线的特征多边形利用4个控制点P0、P1、P2、和Pn,当P1和P2重合为一点时就变成为二次贝塞尔曲线,并且具有更加丰富的形状特征和更强的形状控制功能[4]。因此,笔者基于三次贝塞尔曲线,按图 1所示的图形建立求解。由于贝塞尔曲线应用在涡轮叶片造型方面已经较为成熟,所以笔者不再推导其可行性和合理性。
|
| 图 1 基于三次贝塞尔曲线的叶片型线及控制点描述 Fig.1 Description of blade profile and control points based on cubic Bezier curve |
1.2 叶片型线描述
根据非均匀有理B样条曲线造型,通过定义变量t1、t2、t3及t4可分别求得吸力面多边形中间控制点S1、S2的坐标以及压力面多边形中间控制点P1、P2的坐标。因此根据吸力面贝塞尔曲线特征多边形的顶点S0、S1、S2和Sn的坐标便可得到吸力边的三次贝塞尔曲线表达式,同理可得压力边的曲线表达式。
2 涡轮叶片的数值模拟分析 2.1 物理定义物理定义即定义计算流道模型网格的指定域、流体类型、边界条件及控制求解等[5]。
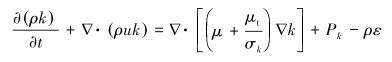
|
(3) |
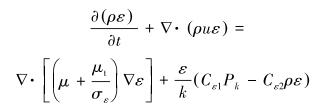
|
(4) |
式中:σk、σε、Cε1、Cε2为常数,k为湍动能,u为速度矢量,ε为湍动能耗散,ρ为密度,t为时间,μ为黏度,ut为湍流黏度,Pk为湍流剪切产出项[4-6]。
2.2 流体域造型、网格划分及边界条件设定通过设定控制点便可得到叶片的吸力面与压力面曲线,进而可以对叶片进行参数化造型。笔者以ø175型涡轮叶片为研究对象,在已知前圆半径、后圆半径、安装角、进出口结构角、叶片数、前楔角、后楔角及相对节距等叶片几何参数的情况下,根据叶片相关理论[6],运用数学软件绘制叶片型线,再由三维实体造型软件建立流道计算模型[4]。叶片设计的前提条件是必须达到涡轮性能指标的基本要求,即涡轮的转速和扭矩需要满足要求;在满足首要条件的基础上尽可能地提高叶片性能。网格划分质量的好坏将直接影响仿真结果的准确性,笔者采用自动网格划分模式,并对涡轮的叶片、薄边以及拐角连接处等进行网格细化,以提高网格质量[7]。同时将叶片流道进、出口分别向上、向下延伸一定距离,以减小单级涡轮模拟与实际流动情况的差异。图 2为涡轮定转子单流道仿真模型图。

|
| 图 2 涡轮定转子单流道仿真模型 Fig.2 Simulation model of single flow channel of turbine stator and rotor |
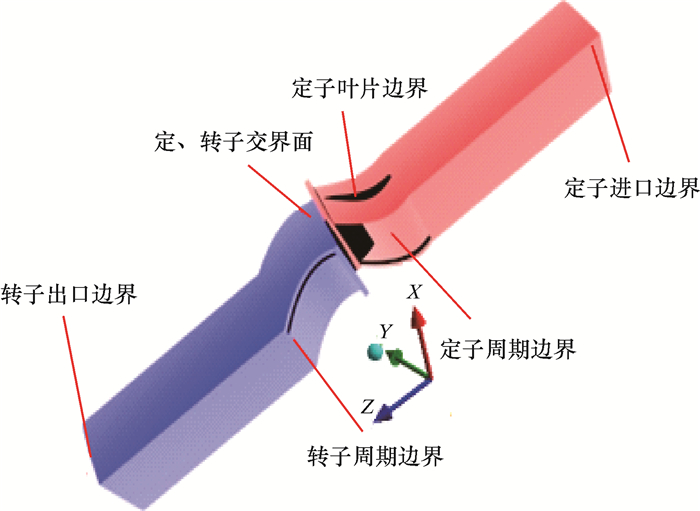
利用CFX-Turbo系统进行数值模拟,其前处理和后处理模块对于涡轮等旋转机械的模拟设定十分方便[7]。在CFX求解过程中,涡轮叶栅内流场选取湍流模型的标准k-ε方程作为控制方程;选取清水为介质,并假定流经叶片的液流为理想流体;给定入口边界条件为入口质量流1.2 L/m,设定定子为静止,设定转子有一个绕Z轴旋转的转速。定、转子周期边界条件设置为周期循环,定转子交界面设置为frozen rotor,其余为无滑移壁面边界条件[7-8]。图 3为流体域边界条件定义图。
|
| 图 3 流体域边界条件定义 Fig.3 Fluid domain boundary condition definition |
2.3 模拟结果与试验验证
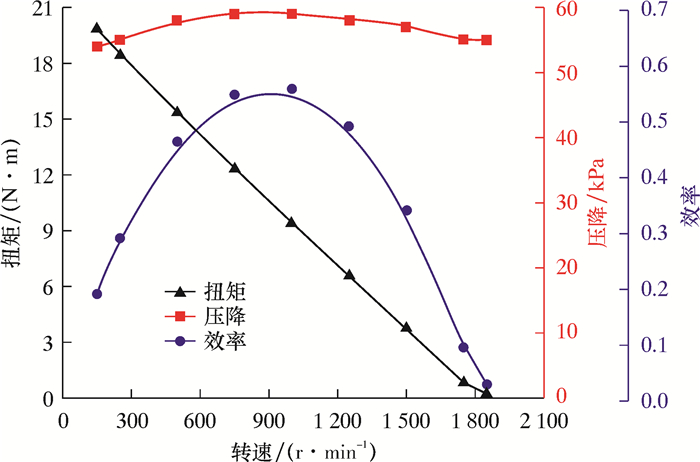
对涡轮内流场进行仿真不仅可以直观地反映流体的运动情况,还可以观测叶片附近流体的脱流和涡流现象,进而详细检测叶片性能。在流体密度和流量给定的情况下,涡轮性能与转速相关。设置固定流量为30 L/s,流体密度为1 000 kg/m3,并考虑容积损失和机械损失造成的能量损失,流体动力黏度为8.899×10-4 Pa·s,分别对不同转速下的内流场进行流体仿真,结果如图 4所示。
|
| 图 4 单副涡轮仿真性能曲线 Fig.4 Single-stage turbine performance curve |
涡轮试验台架系统选用10级涡轮试验系统[9]。试验时以清水介质代替钻井液,设定流量为30 L/s,为降低试验误差,装配10副涡轮进行试验。试验过程中,通过磁粉制动器给主轴施加阻力矩,从而来改变主轴的转速,转速每次改变150 r/min。试验记录的原始测量参数包括流量、压降、扭矩和转速。涡轮的效率使用压降和扭矩等数据进行计算。不同转速下的输入功率Nin(n)和输出功率Nout(n)计算表达式分别为:
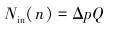
|
(5) |
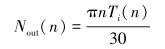
|
(6) |
则效率计算式为:
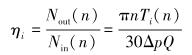
|
(7) |
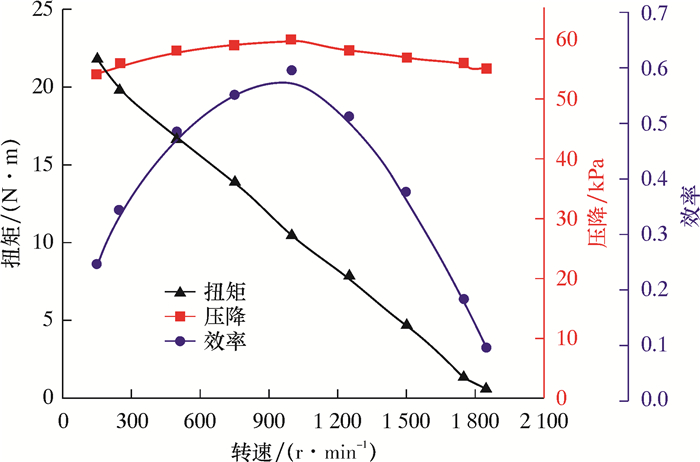
将试验数据转换成单副涡轮的试验结果,并绘成曲线,如图 5所示。对比图 5与图 4发现,CFD数值仿真结果与台架试验结果非常接近。于是得到结论:涡轮的最优转速在900~1 200 r/min,而空转转速在2 000 r/min左右,最优工况下的扭矩为9~12 N·m,压降基本稳定在0.06 MPa。综上所述,通过10副涡轮的试验结果与模拟结果对比充分证明了数值仿真模拟的准确性和正确性。
|
| 图 5 单副涡轮试验的水力性能曲线 Fig.5 Hydraulic performance curve of single-stage turbine |
3 调控设计参数的影响研究
从涡轮叶片结构设计参数来看,尽管其结构十分简单,但其内部流动却十分复杂,影响其性能的结构参数众多,并且参数之间相互制约。目前,涡轮叶片很多参数还没有具体的表达式,大多参数根据航空涡轮和水轮机等方面的相关理论[6, 9]来推算设计,或是参考经验公式、加工工艺和实际工况等方面来综合考虑。贝塞尔曲线造型对叶型调控能力具有灵活性和可控性,为了避免盲目调控,尽可能地选用较少的变量进行叶片的造型研究。笔者给出了几个典型可控的几何设计参数、控制点位置参数以及控制点权因子参数,并分析了安装角和后锥角对涡轮水力性能的影响[9]。
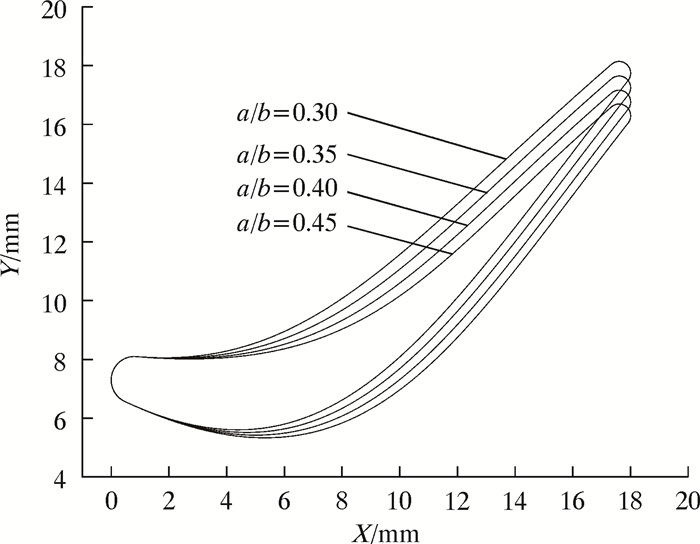
3.1 安装角βm的变化对型线的调整由前文的计算可知,当叶片结构角给定时,调整叶栅最大厚度的相对位置(a/b)即可改变叶片安装角βm。叶片最大厚度的相对位置(a/b)在0.30~0.45区间内,以0.05为间隔做安装角的变化图,如图 6所示。建立不同安装角βm下流道模型,进行CFX数值模拟仿真,结果如图 7所示。
|
| 图 6 影响安装角的参数变化图 Fig.6 Variation of the parameters affecting the installation angle |
|
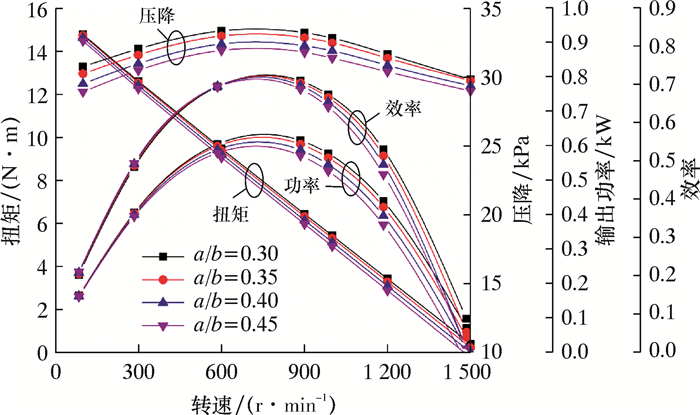
| 图 7 安装角变化对水力性能的影响曲线 Fig.7 Effect of installation angle on hydraulic performance |
分析不同安装角下涡轮特性曲线可知:涡轮最佳工作转速在800 r/min左右,效率可达68%。在低转速时,安装角对输出功率与效率的影响不明显;超过最优转速后,其对输出功率和效率的影响十分显著,并且随着安装角的增大,涡轮的扭矩、压降、输出功率以及效率都呈现降低的趋势。
3.2 后锥角φ2的变化对型线的调整后锥角φ2在7°~15°之间每隔4°取一组值时,型线变化如图 8所示。同理,数值模拟结果如图 9所示。

|
| 图 8 后锥角φ2变化影响叶片变形图 Fig.8 Effect of the back taper angle φ2 on the blade deformation |
|
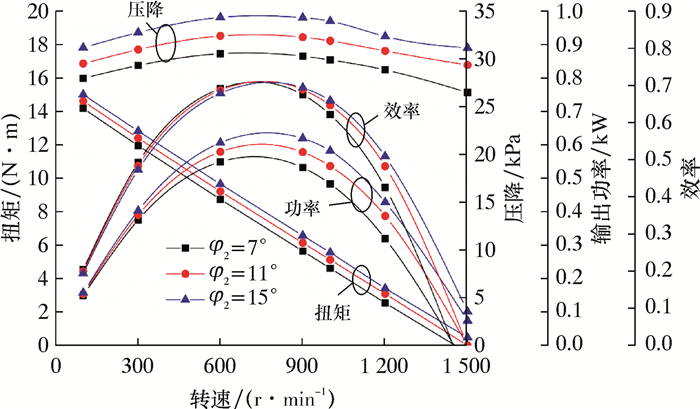
| 图 9 后锥角变化对水力性能的影响图线 Fig.9 Effect of the back taper angle on the hydraulic performance |
分析不同后锥角的特性曲线可得:随着叶片后锥角的增大,扭矩、压降及输出功率都呈现增大趋势,而效率在低转速时呈现减小趋势,超过最优转速后呈现增大的趋势,最优效率可达68%;最优转速情况下,后锥角15°比7°时的扭矩与输出效率分别增大了1 N·m和0.11 kW,分别提高了13.3%和16.5%。因此,涡轮要在最高工作效率下获得较大输出功率,可以适当增大叶片后锥角。
4 结论(1) 提出的数值模拟方法可以系统地实现涡轮叶片从造型设计、性能预测到参数优化的全面分析;涡轮试验台架的试验结果与仿真模拟结果一致性较好,证明了数值模拟计算的准确性。
(2) 通过数值模拟分析了安装角和后锥角对涡轮叶片水力性能的影响。分析结果表明:在低转速时,安装角对输出功率与效率的影响不明显,超过最优转速后其对效率和功率的影响显著,并且涡轮扭矩、压降、输出功率及效率随安装角增大呈降低趋势;随着后锥角增大,扭矩、压降及输出功率都呈增大的趋势,因此涡轮要在最高效率下获得较大输出功率,可适当增大后锥角。
| [1] |
冯进, 符达良. 涡轮钻具涡轮叶片造型设计新方法[J]. 石油机械, 2000, 28(11): 9-12. FENG J, FU D L. A design method of turbine blade shape of turbodrill[J]. China Petroleum Machinery, 2000, 28(11): 9-12. DOI:10.3969/j.issn.1001-4578.2000.11.003 |
| [2] |
张晓东, 余世敏, 龚彦, 等. 基于Bezier曲线的涡轮叶片参数化造型及优化设计[J]. 机械强度, 2015, 37(2): 266-271. ZHANG X D, YU S M, GONG Y, et al. Modeling and optimization for turbine blades based on Bezier curve[J]. Journal of Mechanical Strength, 2015, 37(2): 266-271. |
| [3] |
黄萍, 安利平. 基于Bezier曲线的新型叶片造型技术研究[J]. 燃气涡轮试验与研究, 2008, 21(2): 19-23. HUANG P, AN L P. Research of new blading technique using the Bezier curve[J]. Gas Turbine Experiment and Research, 2008, 21(2): 19-23. DOI:10.3969/j.issn.1672-2620.2008.02.005 |
| [4] |
KORAKIANITIS T, HAMAKHAN L A, REZAIENIA M A, et al. Design of high-efficiency turbomachinery blades for energy conversion devices with the three-dimensional prescribed surface curvature distribution blade design (CIRCLE) method[J]. Applied Energy, 2012, 89(1): 215-227. DOI:10.1016/j.apenergy.2011.07.004 |
| [5] |
张先勇, 冯进. 扭曲叶片涡轮水力性能研究[J]. 煤矿机械, 2015, 36(8): 121-123. ZHANG X Y, FENG J. Research on hydraulic property of twisted blade turbo[J]. Coal Mine Machinery, 2015, 36(8): 121-123. |
| [6] |
张强, 陈治, 罗凯佳, 等. 连续管小尺寸涡轮钻具三维叶栅设计研究[J]. 科学技术与工程, 2016, 16(7): 186-189. ZHANG Q, CHEN Z, LUO K J, et al. Coiled tubing small size turbodrill three-dimensional cascade design[J]. Science Technology and Engineering, 2016, 16(7): 186-189. DOI:10.3969/j.issn.1671-1815.2016.07.030 |
| [7] |
冯进, 张慢来, 刘孝光, 等. 应用CFD软件模拟ø115 mm涡轮钻具机械特性[J]. 天然气工业, 2006, 26(7): 71-73. FENG J, ZHANG M L, LIU X G, et al. CFD simulation of mechanical performance of turbodrill with diameter of 115 minimeter[J]. Natural Gas lndustry, 2006, 26(7): 71-73. DOI:10.3321/j.issn:1000-0976.2006.07.023 |
| [8] |
赵洪波.涡轮钻具涡轮叶栅的水力计算分析[D].北京: 中国地质大学(北京), 2012. ZHAO H B. Hydraulic calculation turbodrill turbine cascade analysis[D]. Beijing: China University of Geosciences(Beijing), 2012. |
| [9] |
谭春飞, 张升峰, 张仁龙, 等. 涡轮叶片型线结构对叶栅流场的影响研究[J]. 石油机械, 2012, 40(12): 6-9. TAN C F, ZHANG S F, ZHANG R L, et al. Research on the effect of turbine blade profile line structure on cascade flow field[J]. China Petroleum Machinery, 2012, 40(12): 6-9. |



