0 引言
近年来,随着海洋油气工业的快速发展,油气多相混输管道的铺设也越来越多,而且随着石油开采由浅水走向深水,管道的铺设深度和长度不断增加。海底管道与平台或陆上终端的多相混输管道系统遇到前所未有的重视。但是气液两相混输管道在输送中可能出现严重的段塞流,段塞流对管道产生周期性的冲击,可能会导致管道甚至平台上的装置破坏。这种破坏由内流致振而产生,故必须用流固耦合方法研究流体运动对固体的影响。
关于单相流体管道的振动问题得到广泛研究[1-4],但对于两相流管道的振动问题,由于流体介质各相的流速和持液率在时间和空间上分布不均匀,流动状态与各参数时刻改变,所以多相流动引起的振动问题极其复杂。对于两相流诱发振动的问题,现有理论多集中于换热器中气液两相流横掠管束的振动研究[5-6],包括周期性流动冲击、流体弹性不稳定、紊流随机激发以及涡激振动,对于内流管道的振动研究相对甚少。张林等[7]利用ANSYS Workbench软件,建立弯管和流体有限元模型,进行流体激励下弯管流固耦合振动特性分析,考察流体波动频率对弯管流固耦合振动幅值的影响。宋学官等[8]基于流固耦合理论,对一段两端固定约束的柔性管道建立流体动力学模型及固体模型,研究结果表明:软管最大主应力和最大应变发生在入口和出口附近,而最大侧向位移发生在软管中央附近。刘勇[9]等以L形管道为例研究以空气-水为流动介质,基于流固耦合求解器和体积分数法(VOF)的组合求解方法,用ADINA软件模拟出气液两相流在L形管道中的流动状态,并分析流体对管道变形的影响。刘昌领等[10]针对一端固定一端简支管道,建立了流固耦合振动控制方程,并用直接解法得到了固有频率、临界流速和临界压力的近似解。通过分析可知,管道长度对固有频率的影响最大,其次是流体速度,液体压力的影响最小;流速、压力等对管道第1阶和第2阶固有频率的影响程度相同。
笔者应用有限元软件ANSYS Workbench,采用VOF模型并结合标准k-ε方程模拟油气管道两相流动,研究由于转向产生动量变化和两相流流动参数脉动而引起的内流致振动的流固耦合现象,并对该管道进行流固耦合模态分析。
1 流固耦合振动基本方程连续流体介质运动的方程可以被表达为连续方程、动量方程。
连续方程:
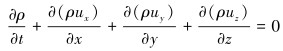
|
(1) |
式中:ρ为流体密度,kg/m3;t为时间,s;ux、uy、uz为3个坐标方向上的速度分量, m/s。
动量方程:
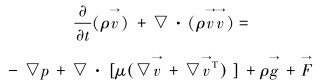
|
(2) |
式中:p为压力;v为速度, m/s;μ为流体黏度,Pa·s; 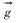
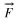
固体有限元振动控制方程为:
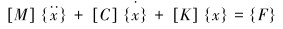
|
(3) |
式中:[M]、[C]、[K]别为质量矩阵、阻尼矩阵以及刚度矩阵;{F}为载荷矩阵;{x}为位移矩阵。
流固耦合遵循最基本的守恒原则,因此在流固耦合交界面处,应满足流体与固体应力、位移等变量的相等或守恒。
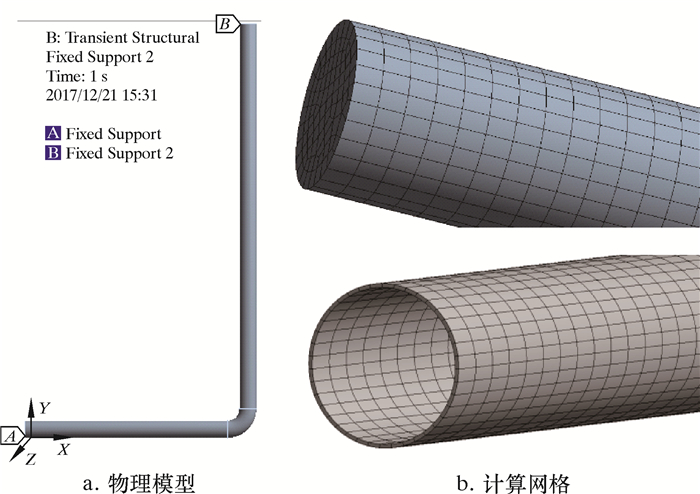
2 有限元模型与CFD模型的建立笔者采用ANSYS Workbench建立直角坐标系下L管有限元分析模型,用Thin命令对弯管内流体抽壳形成管道。管道材料为结构钢,弹性模量为206 GPa,泊松比为0.3,密度为7 850 kg/m3。管道尺寸:短边长5 m,长边长10 m,直径50 mm,壁厚10 mm,弯曲段半径500 mm。A、B两端为管道外固定支撑。管道和流体的局部计算网格见图 1。
|
| 图 1 计算物理模型与流体和管道计算网格 Fig.1 The physical model and the fluid and pipeline calculation grid |
3 气液两相流动分析
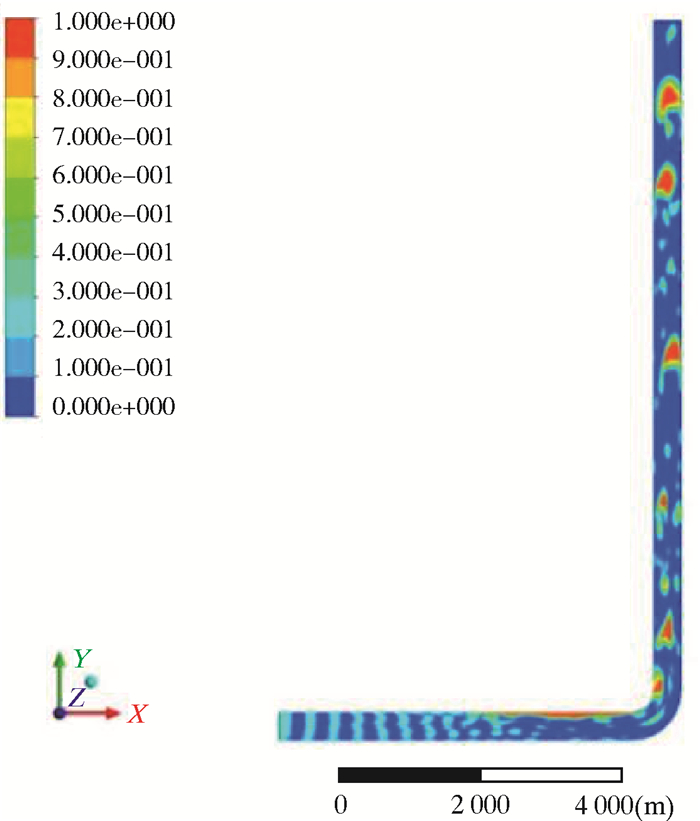
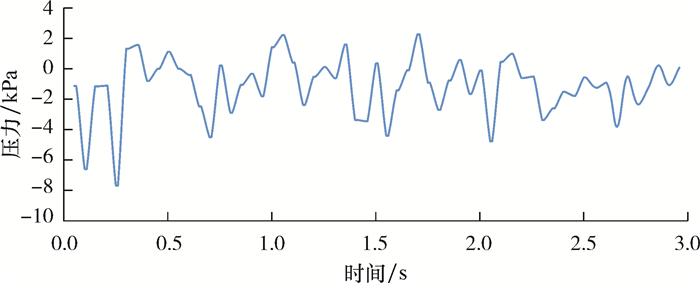
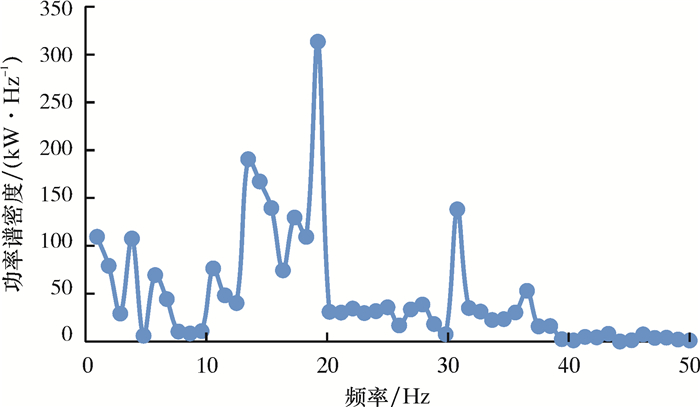
入口气液以3 m/s速度均匀流入,非稳态计算时间3 s。图 2为管道中间截面气相体积分数图,图中蓝色代表液相体积分数,红色为气体体积分数。由图 2可见,两相均匀流入入口后,随着流动向弯头靠近,由于气体密度小,会在水平管道靠上部分形成一个大气团,流过弯头后,在垂直管内形成几个气团。这种流型是段塞流和环状流之间的过渡流型,在水平管中不会产生这种流型。随着流速增加,这种流动的结构形式变得不稳定:流体会往复上下流动,但整体还是向上流动。产生这种不稳定的原因是重力和Taylor气泡对液体薄膜的切向力(与重力方向相反)周期性的动态平衡。在这样的过流截面,若流动参数不均匀则会导致管道振动。图 3为管内两相流3D流线图。由图 3可见,流体通过弯头后流线发生三维螺旋上升,流动在横截面上存在很大的不均匀性。图 4为管道中截面压力分布。由图 4可知,流体水平冲向弯头后动量发生改变,最大压力出现在弯角处,故在弯角处设置监测点检测流动中点的压力,压力的时域数据见图 5。由图 5可见,在计算时间内两相流动压力在管道内周期性重复,经傅里叶转换至频域。压力的功率频谱密度见图 6。由图 6可见,当流动的波动频率位于19 Hz时,监测点产生的功率最大。
|
| 图 2 气相体积分数图 Fig.2 Gas phase volume fraction distribution |

|
| 图 3 三维流线图 Fig.3 Three-dimensional streamline |

|
| 图 4 管道中截面压力分布 Fig.4 Pressure distribution on the pipeline section |
|
| 图 5 管道弯头部分监测点压力时域 Fig.5 Pressure time domain of the monitoring point at pipe elbow part |
|
| 图 6 管道弯头部分监测点压力频域 Fig.6 Pressure frequency domain of the monitoring point at pipe elbow part |
4 L管流固耦合振动分析 4.1 固有频率
现有研究大多采用两端固定管道截面,若弯管两端与容器相连,则两端固支合理。而笔者研究的L管为管系中的一部分,两端不与容器直接相连,故转接头处两端截面固定不合理,采用两端管道外壁固定支撑。两种情况下管道的6阶固有频率对比见表 1。从表 1可见,若采用外壁固定支撑则各阶固有频率下降。
| 阶数 | 两端面固支频率/Hz | 两端线固支频率/Hz |
| 1 | 9.23 | 9.14 |
| 2 | 19.33 | 19.22 |
| 3 | 24.21 | 24.06 |
| 4 | 55.47 | 55.11 |
| 5 | 57.23 | 56.86 |
| 6 | 63.77 | 63.30 |
由于通常情况下1阶和2阶固有频率影响最大,故对比两种支撑下两阶振型可见,1阶与2阶振型皆略有差异。研究发现,1阶频率下管道最大变形主要发生在拐弯处,而2阶频率下管道最大变形发生在垂直部分的中央位置。
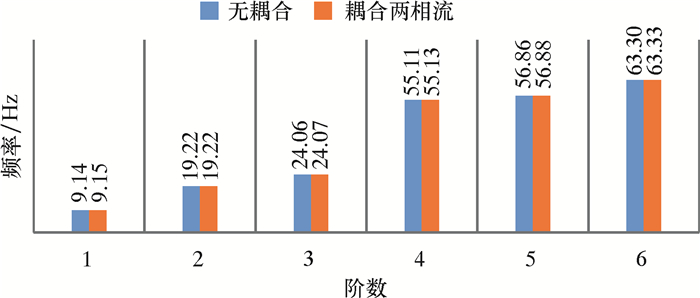
分别进行了管道无预应力的模态分析以及将CFD计算的压力作为预应力加载到管道上的两种计算,得到两种情况下管道的6阶固有频率,如图 7所示。从图 7可见,带有预应力的管道模态计算的频率略有增大,但幅度甚微。分析产生这种现象的原因是,由CFD软件计算出来传给管道3个坐标方向的力分别为:Fx=398.08 N,Fy=-190.85 N,Fz=47.076 N,在模拟情况下,不足以对结构钢产生明显影响。
|
| 图 7 无预应力与加载预应力的6阶固有频率对比 Fig.7 Comparison of 6th-order natural frequencies without/with prestress |
4.2 应力与变形分析
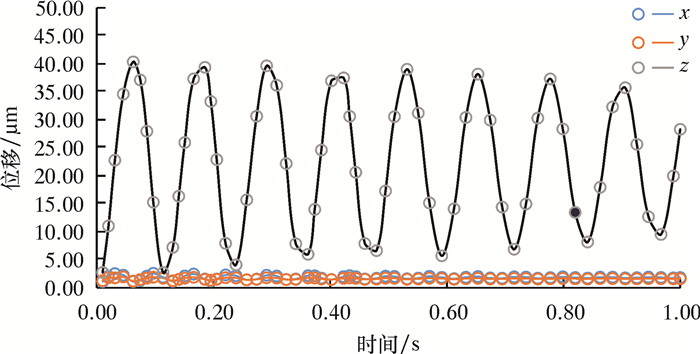
在1阶固有频率下,管道变形最大位移发生在水平管经弯头转接到垂直管处,2阶变形最大位移发生在垂直管的中央位置,故取两阶固有频率的最大位移点为观测点,观察位移与应力的振动情况。下方观测点的3个坐标方向上的位移随时间的变化曲线如图 8所示。图 8中:x方向表示水平方向振动,y方向表示垂直方向振动,z方向则表示与前两者垂直的纵向深度方向的振动,参见图 1的坐标系。由于x方向和y方向产生的振动位移远远小于z方向产生的振动位移,故将x方向和y方向产生的振动位移放大进行比较,如图 9所示。由两图可见,由于两端固定,所以两相流动在竖直方向产生的振动位移最小,在水平方向上的振动幅度次之,最大振动则出现在没有固定约束的z方向。位移振动有自己的固定频率,为防止管道振动,应在z方向加固定约束。
|
| 图 8 观测点1在3个坐标方向上的位移随时间变化曲线 Fig.8 Displacement versus time of the observation point 1 in three coordinate directions |

|
| 图 9 观测点在x、y坐标方向上的位移随时间变化曲线 Fig.9 Displacement versus time of the observation point in the x and y coordinate directions |
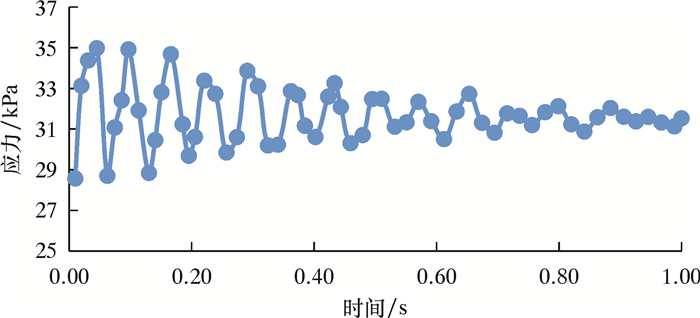
图 10为管道最大位移点应力随时间的周期性变化曲线。
|
| 图 10 监测点应力随时间周期性变化曲线 Fig.10 The stress versus time of the monitoring point |
从图 10可见,监测点应力随时间周期性变化幅度逐渐减小,波动周期约为0.065 s,转换为频率15.38 Hz。该频率接近计算所得管道的固有2阶频率19 Hz,故两相流动的压力变化易引起管道的2阶共振。
5 结论(1) 气液两相流水平冲向弯头后动量发生改变,最大压力出现在弯角处,导致管道应力随时间周期性变化,且变化幅度逐渐减小,频率接近管道的2阶固有频率,易产生共振。
(2) 无预应力的模态分析结果比将CFD计算结果作为预应力加载到管道上得到的管道6阶固有频率小。
(3) L管内两相流动在竖直方向上产生的振动位移最小,在水平方向上的振动幅度次之,最大振动出现在没有固定约束的z方向。因此,为防止管道振动,应在z方向加固定约束。
| [1] |
许超洋.气液两相流混输管道振动分析研究[D].东营: 中国石油大学(华东), 2007. XU C Y. Vibration analysis of gas-liquid two-phase mixed pipeline[D]. Dongying: China University of Petroleum(Huadong), 2007. |
| [2] |
杨再勇, 沙朋朋, 姚青云. 压力管道振动数值模拟分析[J]. 宁夏工程技术, 2016, 15(3): 228-232. YANG Z Y, SHA P P, YAO Q Y. Numerical simulation analysis of pressure pipeline vibration[J]. Ningxia Engineering Technology, 2016, 15(3): 228-232. DOI:10.3969/j.issn.1671-7244.2016.03.008 |
| [3] |
吴钰骅, 金伟良, 龚顺风, 等. 海底管道流固耦合振动数值模拟[J]. 浙江大学学报(工学版), 2009, 43(4): 782-788. WU Y H, JIN W L, GONG S F, et al. Numerical simulation of fluid-solid coupling vibration of submarine pipelines[J]. Journal of Zhejiang University(Engineering Edition), 2009, 43(4): 782-788. |
| [4] |
王武, 陈涛, 杨帅, 等. T型结构压力管道流固耦合模拟与试验验证[J]. 中国安全生产科学技术, 2017, 13(10): 5-11. WANG W, CHEN T, YANG S, et al. Fluid-solid coupling simulation and experimental verification of T-shaped pressure pipelines[J]. China Safety Production Science and Technology, 2017, 13(10): 5-11. |
| [5] |
苏新军, 张修刚, 王栋, 等. 气液两相流横掠错列圆柱形成旋涡脱落诱发管束振动的试验研究[J]. 热能动力工程, 2004, 19(1): 14-16. SU X J, ZHANG X G, WANG D, et al. Experimental study on vibration of tube bundles induced by vortex shedding of gas-liquid two-phase flow across staggered cylinders[J]. Thermal Power Engineering, 2004, 19(1): 14-16. DOI:10.3969/j.issn.1001-2060.2004.01.004 |
| [6] |
马晓旭, 田茂诚, 张冠敏, 等. 水平管内气液两相流诱导振动的数值研究[J]. 振动与冲击, 2016, 35(16): 204-210. MA X X, TIAN M C, ZHANG G M, et al. Numerical study on induced vibration of gas-liquid two-phase flow in horizontal tubes[J]. Vibration and Shock, 2016, 35(16): 204-210. |
| [7] |
张林, 窦益华, 于凯强, 等. 流体激励下弯管流固耦合振动特性分析[J]. 油气井测试, 2017, 26(3): 10-14. ZHANG L, DOU Y H, YU K Q, et al. Analysis of fluid-solid coupling vibration characteristics of elbows under fluid excitation by[J]. Oil and Gas Well Test, 2017, 26(3): 10-14. DOI:10.3969/j.issn.1004-4388.2017.03.003 |
| [8] |
宋学官, 蔡林, 张华. ANSYS流固耦合分析与工程实例[M]. 北京: 中国水利水电出版社, 2012. SONG X G, CAI L, ZHANG H. ANSYS fluid-solid coupling analysis and engineering example[M]. Beijing: China Water Resources and Hydropower Press, 2012. |
| [9] |
刘勇, 郭杰, 孙慧, 等. 基于L形管道的气液两相流-流固耦合模拟计算[J]. 内蒙古石油化工, 2014, 18(1): 1-3. LIU Y, GUO J, SUN H, et al. Fluid solid coupling simulate calculation of gas-liquid two-phase flow based on L type pipeline[J]. Inner Mongolia Petrochemical Industry, 2014, 18(1): 1-3. |
| [10] |
刘昌领, 罗晓兰, 叶道辉, 等. 一端固定一端简支输流管道流固耦合振动分析[J]. 机械与电子, 2013, 31(7): 19-22. LIU C L, LUO X L, YE D H, et al. Fluid-solid coupled vibration analysis of a pipeline with one end fixed and one end simply supported[J]. Mechanics and Electronics, 2013, 31(7): 19-22. DOI:10.3969/j.issn.1001-2257.2013.07.005 |


