0 引言
近年来,我国油气管道建设事业迅猛发展,同时管道安全问题备受关注[1]。管道内检测技术作为保证管道运行安全、提高完整性管理水平的重要手段,在全球范围内得到了广泛应用及认可[2-3]。目前,油气管道内检测技术的具体流程包括普通清管、测径板检测、变形检测器检测和智能检测器检测4个阶段[4]。其中,变形检测器检测和智能检测器检测能够实现里程记录及缺陷点定位等功能。
目前,常规的检测器里程记录和测量的技术包括里程轮测量技术和惯性导航测量技术[5]。对于惯性导航测量技术而言,由于其检测原理的限制,随着检测距离的增加,累积误差也会逐渐增大。因此,通常通过设定外部定位点的方式来对里程进行修正,但该种方式的测量精度与定位点的布置密度以及传感器的精度密切相关,经济性较差、后期数据处理复杂且繁琐。对于里程轮定位技术,其依靠里程轮沿管壁滚动实现距离测量,结构简单且可靠,具有良好的经济性,因此被广泛应用于管道内检测技术中[6]。虽然里程轮测量技术具有以上优点,但不可避免也存在测量误差。由检测原理可知,其误差来源主要包括轮子的打滑、弹跳以及通过管道特殊结构所引起的位移误差等。其中,环焊缝是管道内部最常见的特征之一,里程轮过环焊缝不可避免会产生里程测量误差,大量环焊缝的存在必然导致里程测量的累积误差。因此,基于这样背景,关于里程轮在管道内部运动分析方面的研究越来越多[7]。
D.KIM等[5]提出了一种里程轮过环焊缝误差修正的算法,同时基于该算法设计了一种里程轮系统,并通过试验验证了应用智能检测器后能一定程度上提高里程轮定位的精度。但该算法没有系统地研讨里程轮过环焊缝的具体过程,并基于理想运行条件下提出,具有一定的实际应用局限性。S.SADOVNYCHIY等[7]对里程轮过环焊缝的过程进行了相关试验研究,分别分析了环焊缝形状、检测速度和流体速度对里程轮检测精度的影响。但该研究仅分析了试验结果,并未对里程轮过环焊缝的具体过程进行分析。Z.G.WANG等[8]将里程轮产生的误差进行了分类分析,包括系统误差和随机误差,并基于大量数据分析得出误差数学模型。但该数学模型基于理想假设前提之下,实际应用具有一定局限性。X.LI等[9]提出一种基于基于环焊缝的里程轮误差修正算法,但该方法需提前预知相邻环焊缝直接管段标准长度。M.S.CHOWDHURY等[10]对里程轮过环焊缝误差进行了分析,同时提出了一种里程轮、惯性导航以及外部定位点组合定位的技术,并经行了相关试验研究。该技术虽能提高里程测量的精度,但工作量大且经济性较差。
环焊缝作为导致里程轮测量技术误差的主要来源之一,在里程轮过环焊缝的运动过程以及运动学分析方面的理论研究较少。因此,笔者通过理论分析并与仿真相结合的方法对里程轮过环焊缝的运动学过程进行了分析,这对提高里程轮里程测量精度具有重要的意义。
1 模型建立 1.1 里程轮结构及原理通常,检测器沿管道周向均匀布置3个里程轮。理想情况下,在管道内部运行时,其在弹簧预紧力作用下沿管壁做纯滚动运动。里程轮上安装有霍尔传感器,可以记录里程轮转动的圈数或角度,进而计算得出滚动的距离,以此来记录检测器在管道内部运行的距离。目前,按传感器原理的不同,里程轮可分为磁旋转编码式和脉冲传感式两类。两种传感器的基本原理均为霍尔效应。脉冲传感式里程轮基本结构如图 1所示。其主要包括滚轮、刚性齿轮盘、脉冲霍尔元件、橡胶块、摆臂和弹簧等。
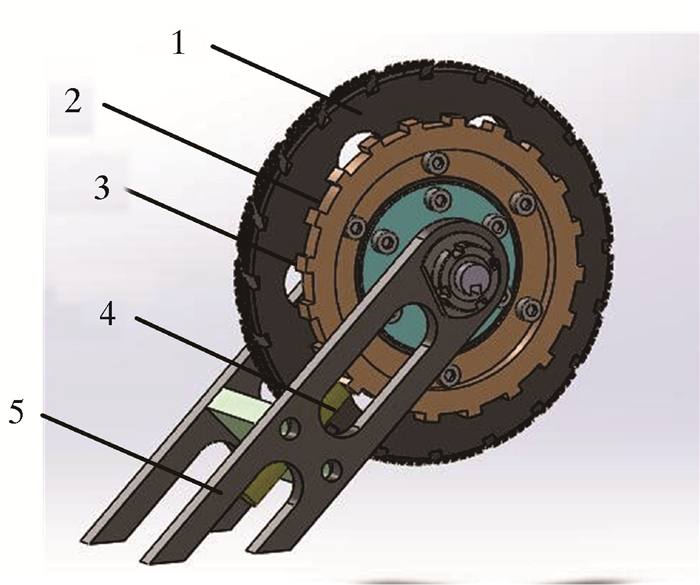
|
| 1—滚轮;2—橡胶块;3—刚性齿轮盘;4—截尔传感器;5—摆臂。 图 1 脉冲传感式里程轮 Fig.1 Pulse sensing odometer |
基于霍尔效应,当轮子转动1周时,传感器记录对应齿数的脉冲。因此,该类里程轮测量精度满足公式(1)。磁旋转编码式里程轮基本结构如图 2所示,其主要包括滚轮、中心轴、磁铁、霍尔元件、弹簧和摆臂等。
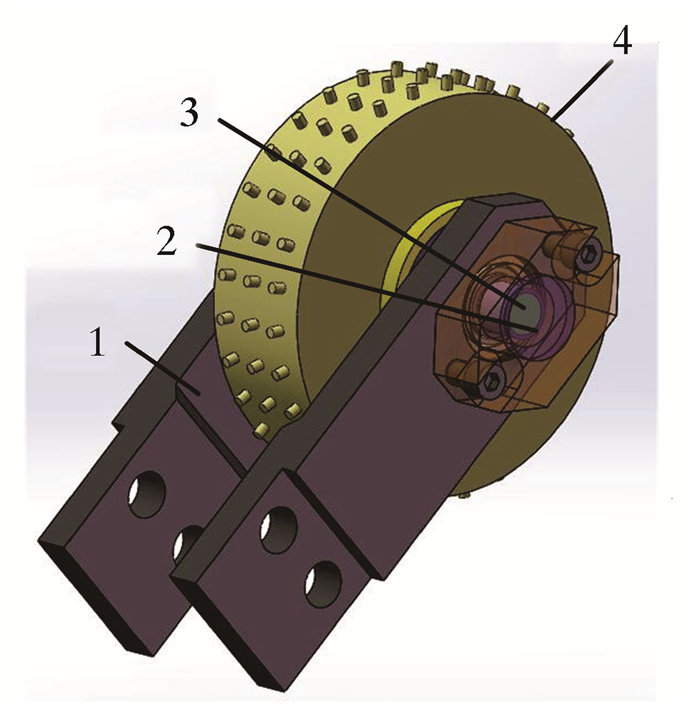
|
| 1—摆臂;2—霍尔元件;3—磁铁;4—滚轮。 图 2 磁旋转编码式里程轮 Fig.2 Magnetic rotary coded odometer |
滚轮与中心轴相对固定,中心轴末端安装有径向磁铁,滚轮滚动过程中,磁铁会在霍尔元件上方产生周期性正弦交变磁场,根据磁场变化记录轮子转动的角度。因此,该类里程轮测量精度满足公式(2)。
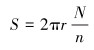
|
(1) |
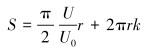
|
(2) |
式中:S为滚动位移,n为齿轮单圈齿数,N为总脉冲数,k为已转过周期数,r为轮子半径,U为霍尔传感器电压值,U0为传感器单周期最大值。
1.2 运动学分析为了更好地研究里程轮过环焊缝的过程,提出以下基本假设:
(1) 根据管道焊接标准,假定环焊缝轮廓为圆弧段;
(2) 忽略系统阻尼。
基于以上假设,里程轮过环焊缝模型简化如图 3所示。其中,环焊缝根据轮廓形状分为上坡段(OP)和下坡段(PQ)两部分。根据运行速度的不同,滚轮的运动轨迹各不相同。
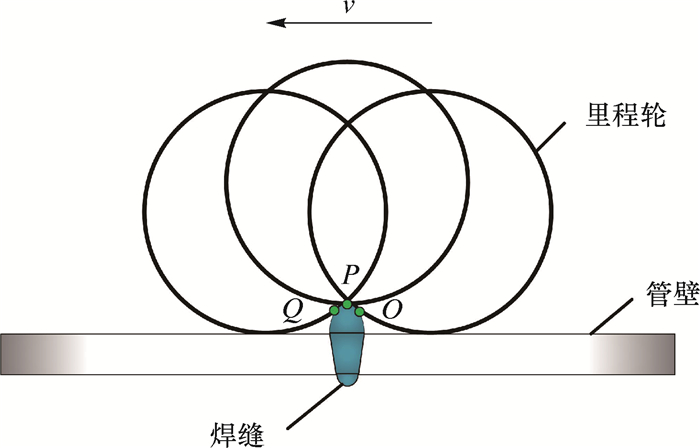
|
| 图 3 里程轮过环焊缝模型图 Fig.3 Model of the odometer passing over girth weld |
当里程轮未与环焊缝接触前,滚轮在轮臂支反力、管壁反作用力和管壁摩擦力共同作用下沿管壁做纯滚动运动,如图 4c所示。当里程轮与环焊缝接触初始时刻,其本质为碰撞过程,且其受力状态如图 4b所示。根据能量守恒定律,碰撞后滚轮的转动角速度瞬间减小,碰撞后角速度满足公式(3)。
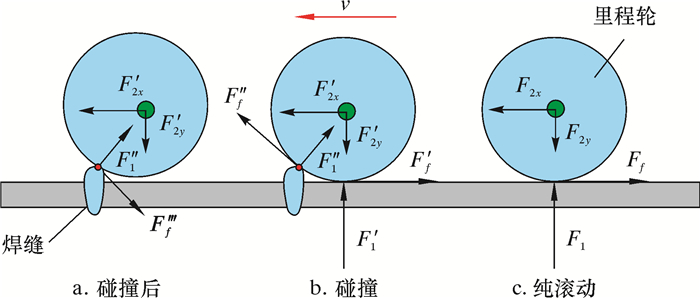
|
| 图 4 里程轮不同状态受力及运动组成分析图 Fig.4 Analysis of the force and motion composition of different states of the odometer |
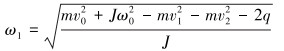
|
(3) |
式中:m为滚轮质量,v0为碰撞前滚轮沿管道轴向运行速度,ω0为碰撞前滚轮角速度,v1为碰撞后滚轮沿管道轴向运行速度,v2为碰撞后滚轮沿管道径向运动速度,ω1为碰撞后滚轮角速度,q为碰撞过程中能量损失,J为滚轮转动惯量。
碰撞结束后,根据检测器运行速度的不同,滚轮与环焊缝分离的时间不同。当低速与环焊缝碰撞时,碰撞后滚轮短时间内与环焊缝重新接触并在检测器的带动下继续沿环焊缝滚动,此时滚轮受到环焊缝的摩擦力方向发生改变,受力状态如图 4a所示。在摩擦力的作用下,滚轮角速度不断增大,此时滚轮角速度满足角动量定理,其角速度增大量Δω满足公式(4)。当高速与环焊缝碰撞时,碰撞后滚轮将产生弹跳现象,进而越过环焊缝后与管壁直接接触,此时在二次碰撞和摩擦力的作用下,里程轮的角速度瞬间增大,直至达到纯滚动角速度大小。
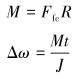
|
(4) |
式中:M为滚轮碰撞后受到的力矩,Ffc为滚轮碰撞后与环焊缝之间的摩擦力,R为滚轮半径,t为碰撞后与环焊缝接触时间。
因此,里程轮过环焊缝的整个过程如下:当检测器低速运行时,里程轮与环焊缝碰撞后,里程轮角速度瞬间减小,碰撞后里程轮继续沿环焊缝运行,在环焊缝摩擦力的作用下角速度逐渐增大直到碰撞前角速度ω0;当检测器高速运行下,里程轮与环焊缝碰撞后,里程轮角速度瞬间减小,同时产生弹跳且越过环焊缝后与管壁接触,在摩擦力作用下角速度增大,直至碰撞前纯滚动角速度ω0。
由于碰撞能量损失难以通过理论计算得出,所以笔者将通过ADAMS多体动力学软件对里程轮过环焊缝的运动学过程进行分析。
2 运动学仿真 2.1 模型仿真在该ADAMS仿真中,里程轮模型如图 5所示。
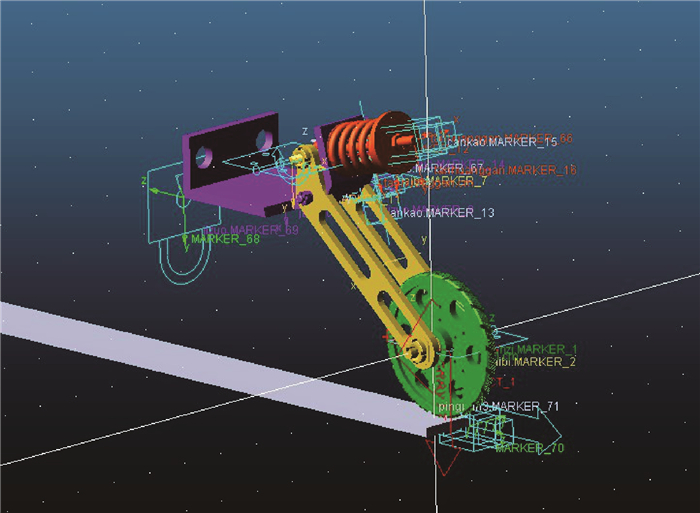
|
| 图 5 基于ADAMS里程轮仿真模型 Fig.5 ADAMS-based simulation model for the odometer |
弹簧采用压缩弹簧结构,弹簧预紧力大小设定为里程轮及轮臂总重力的5倍。管道简化为平板模型,环焊缝布置于平板之上,里程轮与管壁及环焊缝之间静摩擦因数设定为0.3,动摩擦因数设定为0.1,滚轮直径为149 mm,模型设定的环焊缝余高2 mm,球焊缝宽度4 mm。里程轮和环焊缝的材料均设定为结构钢。求解器设定为运动学分析,最大平移增量为1.0×104 mm,最大角度增量30°。滚轮与环焊缝及管壁之间接触法向力设定为接触,刚度1.0×105 N·m,力指数2.2,穿透深度0.1 mm。
根据检测器性能要求,通常运行速度控制在0.5~3.0 m/s范围内检测效果最佳。因此,模型仿真过程中设定里程轮沿管道轴线方向运行速度依次为0.5、1.0、1.5、2.0、2.5和3.0 m/s,测量值分别设定为里程轮质心运动径向Y正向位移以及滚轮角速度值。
2.2 仿真结果及讨论通过建立上述运动学仿真模型,检测器不同运行速度下,里程轮通过环焊缝时沿管道径向的位移值以及滚轮角速度值可以被提取出。
图 6为检测器不同运行速度下,里程轮通过环焊缝时质心的运动轨迹曲线图。由运动轨迹可看出:当检测器处于低速运行过程中(1.5 m/s以下),里程轮与环焊缝接触碰撞后并未产生弹跳分离现象,仍沿环焊缝轮廓继续滚动;随着运行速度的增大,里程轮与环焊缝接触后摆臂产生反向角速度,因此实际运行轨迹的径向极值点高于环焊缝实际高度,并且由曲线可以看出,运行速度越大,里程轮质心径向和轴向位移值越大,进而里程轮产生的测量误差也越大。
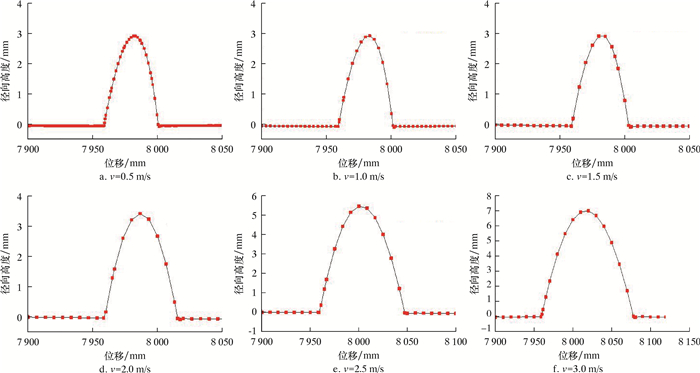
|
| 图 6 里程轮不同速度过环焊缝时质心轨迹图 Fig.6 Mass center trajectory diagram of the odometer passing over the girth weld at different speeds |
图 7为检测器不同运行速度下,里程轮通过环焊缝时滚轮角速度变化曲线图。从图 7可以看出,里程轮过环焊缝角速度变化大致可分为3类,分别为低速阶段(1 m/s以下)、中速阶段(1~2 m/s)和高速阶段(2 m/s以上)。下面将分别对这3种情况进行分析讨论。
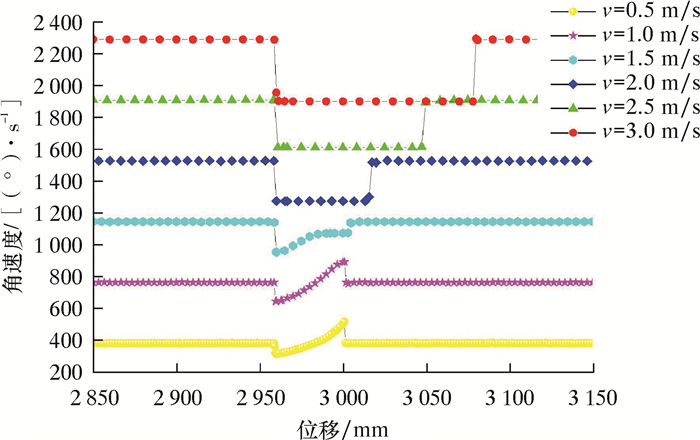
|
| 图 7 里程轮过环焊缝时滚轮角速度变化图 Fig.7 Angle velocity variation of the odometer passing over the girth weld |
图 8为里程轮以0.5 m/s过环焊缝时滚轮角速度变化图。从图 8可以看出,滚轮角速度变化趋势分为3个阶段,分别为先减小、再增大后再减小。其中,第一阶段为图中AB段,该过程即为里程轮与环焊缝接触阶段,该过程由于碰撞作用产生能量损失,并且环焊缝摩擦力对里程轮做负功,所以里程轮角速度幅值瞬间减小。第二阶段为图中BC段,该过程里程轮继续沿环焊缝表面运行,此时由于滚轮所受摩擦力方向发生变化,所以在正功的作用下,里程轮角速度逐渐增大。第三阶段为图中CD段,该过程里程轮再次与管壁接触,此时由于滚轮角速度大于纯滚动角速度值,受到摩擦力方向再次改变且做负功,直到减小到纯滚动角速度值后保持不变。
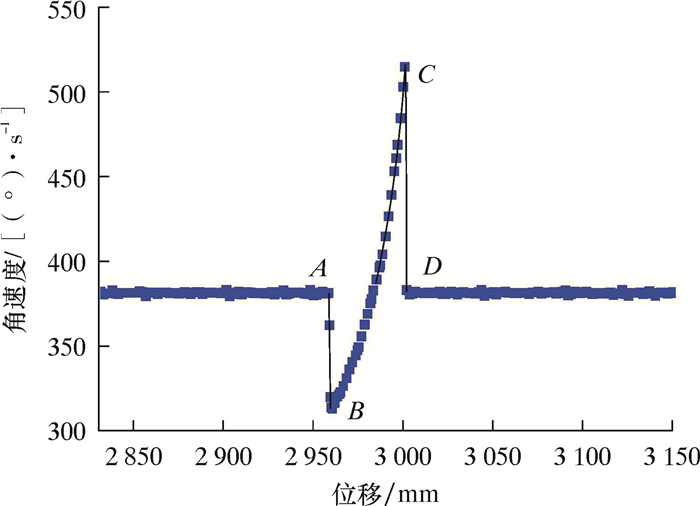
|
| 图 8 里程轮以0.5 m/s过环焊缝时角速度变化图 Fig.8 Angle velocity variation of the odometer passing over the girth weld at the velocity of 0.5 m/s |
图 9为里程轮以1.5 m/s过环焊缝时角速度变化图。从图 9可以看出,滚轮角速度变化趋势也分为4个阶段,分别为快速减小、缓慢增大、速度保持恒定、快速增大。第一阶段为图中EF段,该过程即为里程轮与环焊缝接触碰撞阶段,但与低速阶段不同的是,该阶段由于里程轮沿管道轴线方向运行速度较大,碰撞产生的能量损失也远大于低速阶段,因此相对比低速阶段和中速阶段碰撞后角速度减小量更大。第二阶段为图中FG段,该过程里程轮同样在环焊缝摩擦力作用下做正功,因此角速度逐渐增大。第三阶段为GH段,该过程滚轮脱离环焊缝,由基本假设可知,在忽略系统阻尼的情况下滚轮角速度将保持恒定不变。第四阶段为HI段,该过程为滚轮与管壁接触过程,该过程与低速运行第3阶段相反,此时由于滚轮角速度小于纯滚动角速度值,所以受到摩擦力做正功,直到增大到纯滚动角速度值后保持不变。
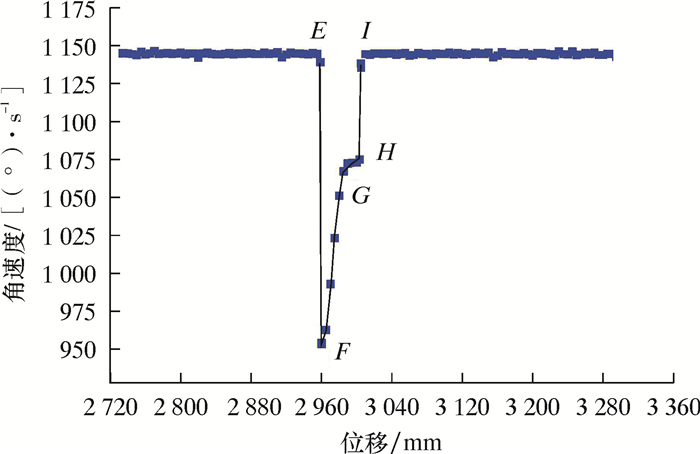
|
| 图 9 里程轮以1.5 m/s过环焊缝时角速度变化图 Fig.9 Angle velocity variation of the odometer passing over the girth weld at the velocity of 1.5 m/s |
图 10为里程轮以3 m/s过环焊缝时角速度变化图。高速阶段与中速阶段有相似之处,但由于运行速度不同,所以碰撞后产生的能力损失以及碰撞后的运行状态不尽相同。从图 10可以看出,滚轮角速度变化趋势分为3个阶段,分别为快速减小、恒定不变和快速增大。第一阶段为JK段,该过程即为滚轮与环焊缝碰撞阶段。第二阶段KL段即为滚轮与环焊缝脱离阶段,该阶段滚轮不受外力作用,因此速度保持恒定不变。第三阶段为LM阶段,该阶段与中速运行第三阶段相似,该阶段滚轮在管壁摩擦力作用下角速度增大,达到纯滚动角速度值后保持不变。
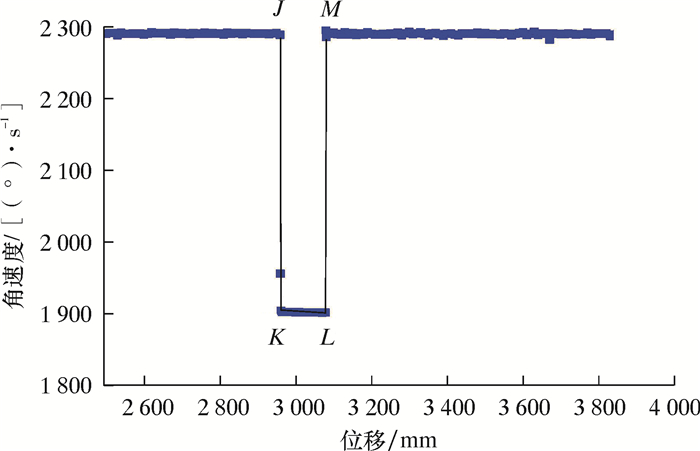
|
| 图 10 里程轮以3 m/s过环焊缝时角速度变化图 Fig.10 Angle velocity variation of the odometer passing over the girth weld at the velocity of 3 m/s |
通过对里程轮过环焊缝模拟结果的分析可知,其运动过程与前文所述结论一致,进而证明基于ADAMS的里程轮运动学仿真的正确性和可靠性。研究结果为里程轮过环焊缝的误差分析提供了理论基础。
3 结论(1) 理论分析了里程轮过环焊缝时的运动学过程,进而通过ADAMS多体动力学软件数值模拟了过环焊缝过程中的滚轮运动轨迹以及角速度变化规律。
(2) 分析结果表明:里程轮过环焊缝运动轨迹受运动速度影响很大,速度越高,产生的里程测量误差具有先减小后增大的趋势;速度不同,引起滚轮与环焊缝的碰撞能量损失不同,进而造成滚轮角速度的变化规律也不相同;运行速度较低时,环焊缝摩擦力会对滚轮做正功,运行速度较高时,滚轮与环焊缝脱离产生空转现象,进而造成较大的里程测量误差。
(3) 研究成果对里程轮过环焊缝误差分析提供了理论依据,对提高内检测器检测数据定位精度具有重要意义。
| [1] |
高鹏, 高振宇, 杜东. 2017年中国油气管道行业发展及展望[J]. 国际石油经济, 2018, 26(3): 21-27. GAO P, GAO Z Y, DU D. Development and prospect of China's oil and gas pipeline industry in 2017[J]. International Petroleum Economy, 2018, 26(3): 21-27. DOI:10.3969/j.issn.1004-7298.2018.03.003 |
| [2] |
王璞, 田富俊. 油气管道安全与环境风险监控预警法规研究[J]. 西南石油大学学报(社会科学版), 2018, 20(1): 19-28. WANG P, TIAN F J. Study on regulations of monitoring and warning of oil and gas pipeline safety and environmental risk[J]. Journal of Southwest Petroleum University (Social Sciences Edition), 2018, 20(1): 19-28. |
| [3] |
沙胜义, 项小强, 伍晓勇, 等. 输油管道环焊缝超声波内检测信号识别[J]. 油气储运, 2018, 37(7): 757-761. SHA S Y, XIANG X Q, WU X Y, et al. Ultrasonic ILI signal identification technology for girth weld defects of oil pipelines[J]. Oil & Gas Storage and Transportation, 2018, 37(7): 757-761. |
| [4] |
代莉莎, 张仕民, 朱霄霄, 等. 油气管道通径检测器技术研究进展[J]. 油气储运, 2012, 31(11): 808-813. DAI L S, ZHANG S M, ZHU X X. Research progress of pipeline path detector technology[J]. Oil & Gas storage and transportation, 2012, 31(11): 808-813. |
| [5] |
KIM D, PARK S, CHO S, et al. Development and measurement error compensation of odometer system for intelligent PIG[J]. J. Korean Inst. Gas, 2002, 6(1): 17-23. |
| [6] |
ZHU X X, LI X L, ZHAO C H, et al. Dynamic simulation and experimental research on the motion of odometer passing over the weld[J]. Journal of Natural Gas Science and Engineering, 2016(30): 205-212. |
| [7] |
SADOVNYCHIY S, LOPEZ J. Improvement of pipeline odometer system accuracy[C]//Canadian International Petroleum Conference.Ottawa: Petroleum Society of Canada, 2005.
|
| [8] |
WANG Z G, TAN J, SUN Z C, et al. Error factor and mathematical model of positioning with odometer wheel[J]. Adv. Mech. Eng., 2015, 7(1): 305981. DOI:10.1155/2014/305981 |
| [9] |
LI X, ZHANG S M, LIU S H, et al. Research for distance measurement of offshore pipeline defects[C]//The Twenty-fifth International Offshore and Polar Engineering Conference.[S.l.]: International Society of Offshore and Polar Engineers, 2015.
|
| [10] |
CHOWDHURY M S, ABDEL-HAFEZ M F. Pipeline inspection gauge position estimation using inertial measurement unit, odometer, and a set of reference stations[J]. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech Eng, 2016, 2(2): 021001-1. |


