2. 中国石油大学(北京)石油工程学院
2. College of Petroleum Engineering, China University of Petroleum(Beijing)
0 引言
页岩气以非常规天然气的形式进入人们的视野,页岩地层基质渗透率和孔隙度极低,需要用水力压裂方法改造地层,提高地层渗流能力[1-5]。页岩体积压裂与常规储层形成高导流能力的水力主缝不同,页岩地层压裂的主要目的是尽可能地形成复杂裂缝网络,体积压裂技术展示了很强的地层改造能力[6]。然而在四川长宁和威远地区页岩气井水力压裂时套管损坏现象频发,极大降低了该区域页岩气的开采效率[7-8]。据现场资料,截至2016年3月,四川长宁威远地区90口水平井压裂过程中发现套损井数量高达30口,套损率为33.3%,单井套管变形点为1~3个。套管损坏后,导致压裂封堵桥塞下入遇阻,不能到达预定位置,致使作业时间延长,严重时甚至被迫放弃部分压裂井段,给油田造成了巨大的经济损失。
对于地层滑移导致剪切型套损的大范围发生,国内外学者对其形成机理进行了多年的研究,并取得了一定的成果[9-14]。刘扬等[15]采用有限元方法对井下套管的弯曲变形进行了数值模拟研究,分析了井下套管的弯曲变形与有效通径、水泥环和地层岩石的破坏范围之间的关系。任思齐等[16]应用多物理场耦合数值模拟软件对热采井套管的热固耦合问题进行了数值模拟研究。寇永强[17]利用数值模拟方法分析了油田开发过程参数与套管的变形破坏的关系,定量考察了断层性质、储层的岩石力学参数以及开发参数变化对套管位移、等效应力的影响规律。上述研究为探究页岩气井套变机理提供了可借鉴的思路,但没有从裂缝的角度着手来探寻套管剪切变形的机理。
为此,笔者针对地层滑移导致页岩气水平井套管损坏的现象,结合套损井的现场资料,以岩石力学试验为基础,利用COMSOL数值模拟软件建立了多裂缝模型,对页岩气水平井在水力压裂过程中地层沿裂缝的滑移变形进行了数值模拟研究,定量地分析了缝内流体压力、裂缝倾角和裂缝间距等参数与地层滑移量之间的关系。研究成果对认识页岩气井剪切型套管变形及对如何预防套管损坏具有一定的理论指导意义。
1 W井压裂概况W井位于四川省境内,为一口页岩气水平井,目的层为志留系龙马溪组页岩。地应力状态为最大水平主应力50 MPa,最小水平主应力40 MPa。在压裂设计时,共设计压裂井段21段,但在实际压裂施工作业中,由于发生套管损坏最终被迫放弃压裂井段6段,实际压裂井段15段。第12段压裂完成后,在井深4 155 m处发生套管变形,泵送直径103.2 mm桥塞时在该井深处遇阻,遇阻井段为4 155~4 162 m。从该遇阻区域自然伽马曲线中可以发现,套损井段从龙1-b段延伸至龙1-a段,穿越了岩性界面。同时微地震监测资料显示,该井段在压裂过程中产生了大量的微地震事件,说明该处存在明显的裂缝带。因此,页岩气水平井压裂过程中套损的发生与天然裂缝的存在有关。
2 龙马溪组页岩三轴力学试验岩石力学参数是解决许多石油工程技术的基础数据,对解决水力压裂过程中的套管损坏问题有着重要的意义。为了更好地进行后续页岩气水平井压裂过程中地层滑移数值模拟研究工作,获得数值模拟所需的基础数据,选取了W井的龙马溪组页岩标准岩芯36块共4组进行了三轴岩石力学试验。
三轴试验采用中国石油大学(北京)重点实验室的岩石力学参数试验装置,该装置由围压加载系统、轴向加载系统和数据自动采集控制系统等三大部分组成。4组试验岩心分别采用与层理方向为0°、45°、60°和90°进行制备。每组岩心所施加围压不同,具体参数设置及试验结果见表 1。
| 层理方向/ (°) | 围压/ MPa | 三轴抗压强度/MPa | 静态弹性模量/GPa | 静态泊松比 |
| 30 | 192.16 | 24.91 | 0.32 | |
| 0 | 50 | 247.13 | 24.45 | 0.33 |
| 70 | 293.73 | 32.94 | 0.32 | |
| 30 | 241.42 | 32.03 | 0.26 | |
| 45 | 50 | 282.16 | 31.95 | 0.30 |
| 70 | 324.41 | 32.20 | 0.32 | |
| 30 | 225.60 | 29.13 | 0.30 | |
| 60 | 50 | 269.55 | 26.56 | 0.32 |
| 70 | 262.15 | 30.79 | 0.32 | |
| 30 | 262.31 | 35.51 | 0.29 | |
| 90 | 50 | 279.20 | 34.38 | 0.23 |
| 70 | 335.44 | 34.18 | 0.32 |
由表 1可知,不同层理方向的岩石其三轴抗压强度、弹性模量和泊松比差别较大。相同层理方向的岩石在不同围压条件下抗压强度、弹性模量和泊松比也不同,存在比较大的差异。在围压为50 MPa时,W井岩样的平均抗压强度为269.51 MPa,平均弹性模量为29.34 MPa,平均泊松比为0.30。
3 地层滑移有限元分析 3.1 建立模型基于上述W井的原始地层资料建立了地层沿裂缝滑移有限元模型,如图 1所示。
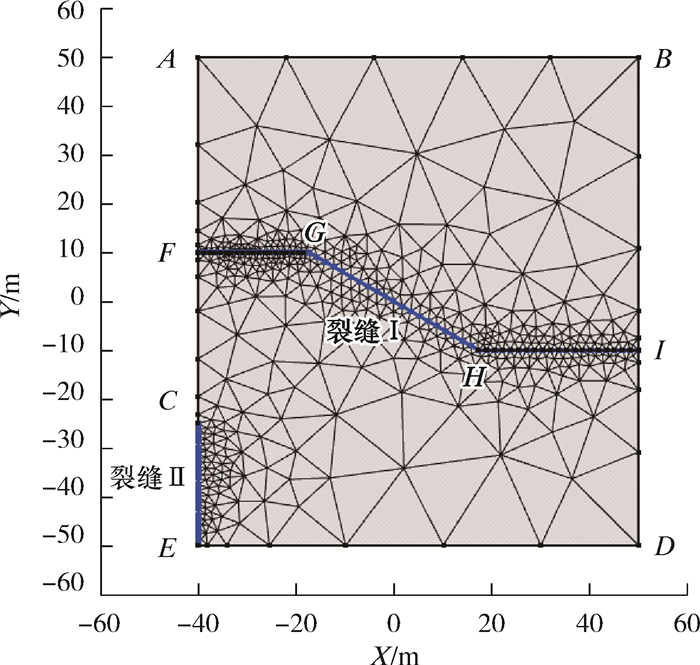
|
| 图 1 地层沿裂缝滑移模型 Fig.1 Model of formation slip along fracture |
在所建立的模型中存在有两条裂缝,裂缝Ⅰ和裂缝Ⅱ,并且W井井眼轨迹穿过裂缝Ⅰ。在体积压裂过程中,裂缝Ⅰ和裂缝Ⅱ会受到周围地应力变化的影响而发生滑移变形,同时裂缝Ⅰ和裂缝Ⅱ相互之间会因为某一应力状态的变化对另一个裂缝产生影响。在该模型中,边界条件:AC、DE为对称边界,FG、HI为连续边界,GH为接触边界。初始条件根据上述三轴岩石力学试验和现场数据确定,具体参数为:弹性模量29.34 GPa,泊松比0.30,地层密度2 300 kg/m3,裂缝Ⅰ倾角30°,裂缝Ⅰ半长20 m,裂缝Ⅱ半长25 m,边界AB长50 m,边界BD长50 m,最大水平主应力50 MPa,最小水平主应力40 MPa,裂缝Ⅰ缝内压力20 MPa,裂缝Ⅱ缝内压力60 MPa。
3.2 模拟结果分析 3.2.1 单一裂缝缝内流体压力的影响在水力压裂过程中,当压裂液进入到地层裂缝中,会使裂缝缝内流体压力发生变化,从而引起裂缝面周围的应力条件发生变化,此时裂缝面受到不均匀载荷的影响,裂缝会沿着应力弱面发生滑移。因此,在数值模拟时通过改变缝内流体压力的大小,得出了不同流体压力条件下地层沿裂缝的滑移情况。图 2是不同流体压力作用下裂缝面沿x方向和y方向的位移量。由模拟结果可知,随着缝内流体压力的增大,裂缝面的滑移量增大。具体表现为:当缝内流体压力为50 MPa时,裂缝面的滑移量达到厘米级,为1.3 cm;当缝内流体压力为60 MPa时,裂缝面的滑移量为2.5 cm;当缝内流体压力为70 MPa时,裂缝面的滑移量达到3.6 cm。总体上,随着缝内流体压力的升高,裂缝的滑移量也会持续增大。缝内流体压力与裂缝滑移量的关系如图 3所示。
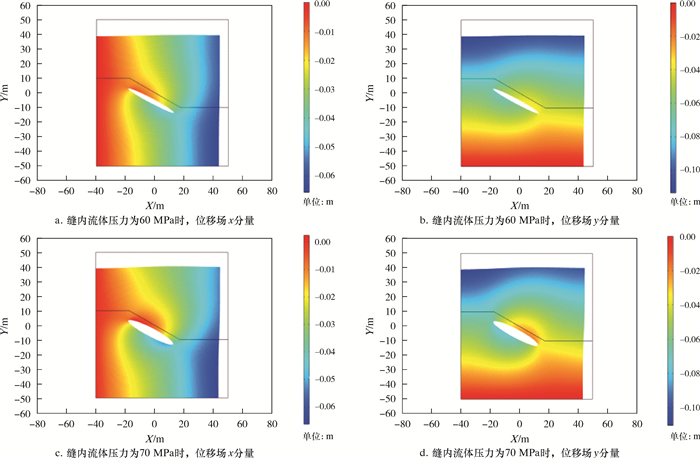
|
| 图 2 缝内流体压力分别为60和70 MPa时位移量云图 Fig.2 Displacements of slippage under the fracture fluid pressure of 60 and 70 MPa |
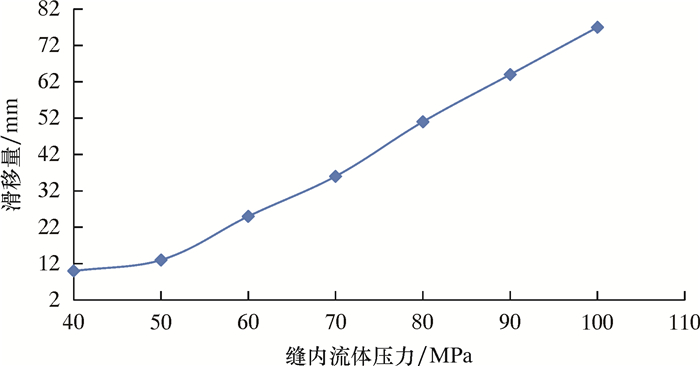
|
| 图 3 不同缝内流体压力条件下裂缝面的滑移量 Fig.3 Slippage of fracture surface under different fracture fluid pressure |
3.2.2 裂缝Ⅱ缝内流体压力的影响
数值模拟过程中发现,当裂缝Ⅱ缝内流体压力发生改变时,由于应力的传递和叠加效果会影响裂缝Ⅰ周围的应力分布,最终导致裂缝Ⅰ的滑移量发生变化。因此,对裂缝Ⅱ的缝内流体压力进行不同取值,得到了裂缝Ⅰ裂缝面沿x方向和y方向的位移量变化情况,如图 4所示。由模拟结果可知:当裂缝Ⅱ缝内流体压力为40 MPa时,裂缝Ⅰ裂缝面的滑移量为5 mm;当裂缝Ⅱ缝内流体压力为60 MPa时,裂缝Ⅰ裂缝面的滑移量为8 mm;当裂缝Ⅱ缝内流体压力达到80 MPa时,裂缝Ⅰ裂缝面的滑移量达到了厘米级,为1.05 cm,说明此时裂缝Ⅱ缝内流体压力的改变已经对裂缝Ⅰ产生了比较明显的影响。
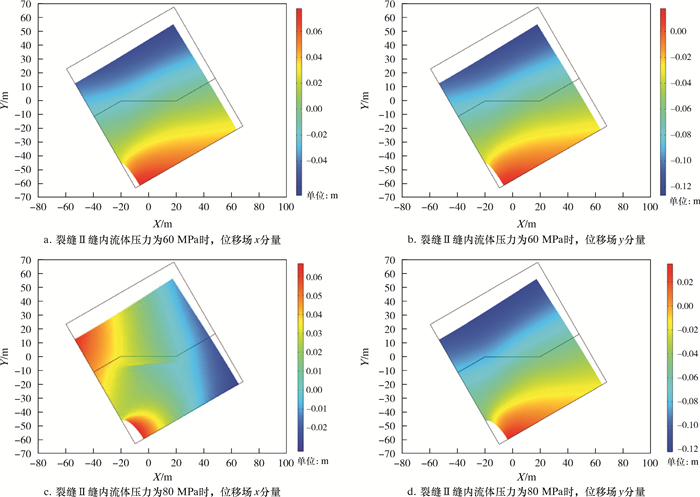
|
| 图 4 裂缝Ⅱ流体压力为60和80 MPa时位移量云图 Fig.4 Displacements of slippage of fracture Ⅱ under the fracture fluid pressure of 60 and 80 MPa |
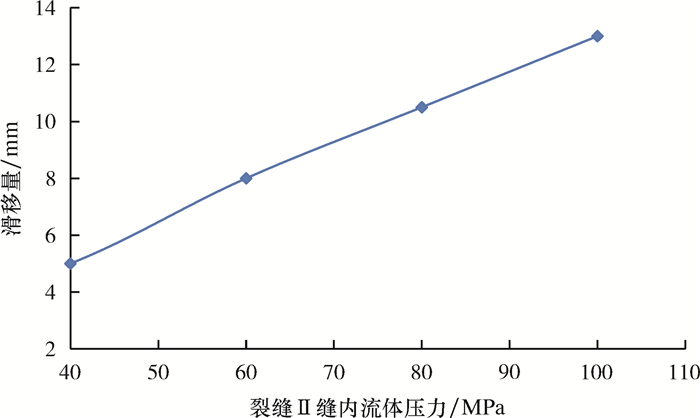
同时通过计算可以发现,当裂缝Ⅱ缝内流体压力继续升高时,裂缝Ⅰ裂缝面的滑移量会持续增加,如图 5所示。
|
| 图 5 裂缝Ⅰ滑移量随裂缝Ⅱ缝内流体压力的变化情况 Fig.5 Variation of the slippage of fracture Ⅰ under the fluid pressure of the fracture Ⅱ |
3.2.3 裂缝Ⅰ、Ⅱ之间夹角的影响
为了解裂缝Ⅰ、Ⅱ之间夹角的变化对裂缝Ⅰ滑移量的影响情况,模拟时固定裂缝Ⅱ缝内流体压力为60 MPa,通过改变裂缝Ⅰ的倾角来实现裂缝Ⅰ、Ⅱ之间夹角的变化,从而得出两裂缝不同夹角条件下裂缝Ⅰ滑移量的变化情况。裂缝Ⅰ的滑移量如图 6所示。在不同夹角条件下,裂缝Ⅰ裂缝面沿x方向的位移量云图如图 7所示。
|
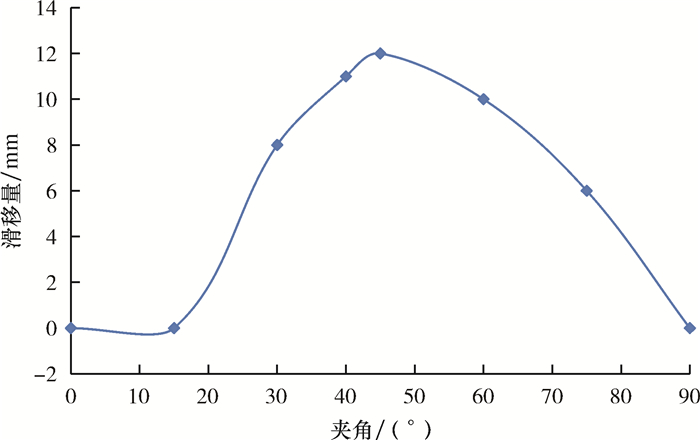
| 图 6 滑移量随裂缝之间夹角的变化情况 Fig.6 Variation of the slippage with the angle between the fractures |
|
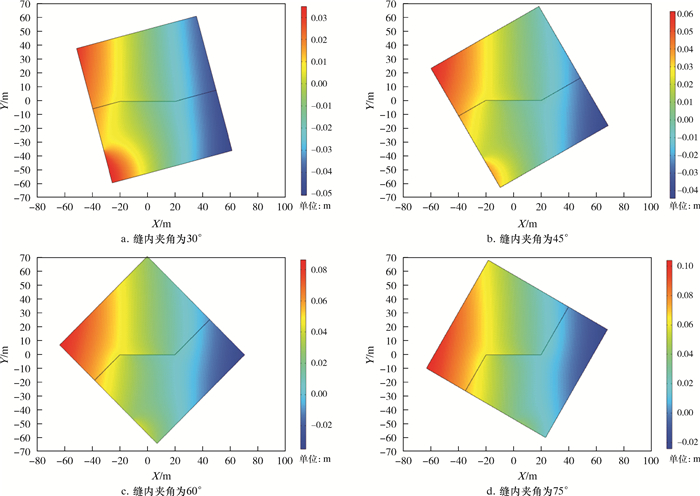
| 图 7 裂缝夹角为30°、45°、60°、75°时x方向位移量云图 Fig.7 Displacement of slippage under the fracture angle of 30°, 45°, 60° and 75° |
由模拟结果可知:当夹角为0°、15°和90°时,裂缝Ⅰ基本没有发生滑移,滑移量为零;但当夹角在15°~90°之间变化时,裂缝Ⅰ裂缝面的滑移量先增大后减小;在夹角为45°时,裂缝Ⅰ裂缝面的滑移量达到最大值为1.2 cm,此时裂缝Ⅱ对裂缝Ⅰ的滑移量影响最为明显。因此,可以发现两裂缝之间的夹角越接近45°,两者之间的影响越明显。
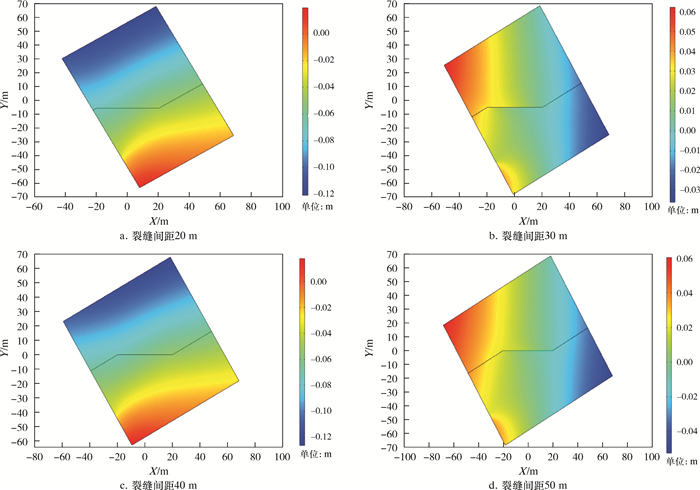
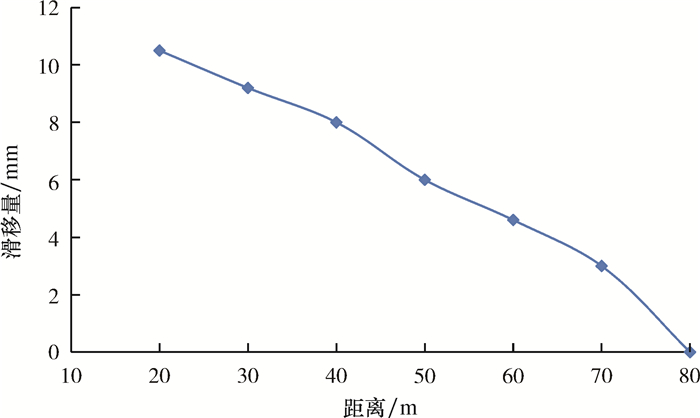
3.2.4 裂缝Ⅰ、Ⅱ之间距离的影响为探究裂缝Ⅰ、Ⅱ之间距离对裂缝滑移量的影响,模拟过程中固定裂缝Ⅰ的位置不变,通过改变裂缝Ⅱ的位置来实现裂缝之间距离的变化,进而得到裂缝Ⅰ裂缝面沿x方向和y方向的位移量云图,如图 8所示。裂缝Ⅰ的滑移量如图 9所示。由模拟结果可知,随着两裂缝之间距离的增加,裂缝Ⅰ的滑移量变小,当两者距离达到80 m时,裂缝Ⅰ的滑移量基本为0,也就是说此种情况下裂缝Ⅱ对裂缝Ⅰ的滑移量基本没有影响。
|
| 图 8 裂缝间距为20、30、40和50 m时x方向位移量云图 Fig.8 Displacement of slippage under the fracture spacing of 20, 30, 40 and 50 m |
|
| 图 9 滑移量随裂缝间距离的变化情况 Fig.9 The slippage as a function of the distance between the fractures |
4 结论
(1) 对于单一裂缝,随着缝内流体压力升高,地层沿裂缝面的滑移量增大,缝内流体压力为50 MPa时,裂缝面的滑移量可以达到厘米级,其值为1.3 cm。
(2) 当存在多条裂缝时,单一裂缝内流体压力的改变会导致邻近裂缝应力场和滑移量的改变,当缝内流体压力达到80 MPa时,对邻近裂缝可产生比较明显的影响。
(3) 当存在多条裂缝时,两条裂缝之间的夹角越接近45°,裂缝与裂缝之间的影响越明显,并且随着裂缝之间距离的增加,裂缝之间的影响越小,当两者距离达到80 m时,裂缝之间基本没有影响。
| [1] |
琚宜文, 卜红玲, 王国昌. 页岩气储层主要特征及其对储层改造的影响[J]. 地球科学进展, 2014, 29(4): 492-506. JU Y W, BU H L, WANG G C. Main characteristics of shale gas reservoirs and their effects on reservoir reformation[J]. Advances in Earth Science, 2014, 29(4): 492-506. |
| [2] |
张东晓, 杨婷云. 页岩气开发综述[J]. 石油学报, 2013, 34(4): 792-801. ZHANG D X, YANG T Y. An overview of shale-gas production[J]. Acta Petrolei Sinica, 2013, 34(4): 792-801. |
| [3] |
王素兵, 罗炽臻. 页岩气藏改造技术及四川页岩气藏压裂先导性试验[J]. 天然气勘探与开发, 2012, 35(1): 65-68, 83. WANG S B, LUO C Z. Shale-gas reservoir treatment technology and pilot test of shale-gas reservoir fracturing in Sichuan basin[J]. Natural Gas Exploration and Development, 2012, 35(1): 65-68, 83. DOI:10.3969/j.issn.1673-3177.2012.01.015 |
| [4] |
张东晓, 杨婷云. 美国页岩气水力压裂开发对环境的影响[J]. 石油勘探与开发, 2015, 42(6): 801-807. ZHANG D X, YANG T Y. Environmental impact of shale gas hydraulic fracturing development in the United States[J]. Petroleum Exploration and Development, 2015, 42(6): 801-807. |
| [5] |
Ground Water Protection Council and All Consulting. Modern shale gas development in the United States: a primer[R]. Oklahoma City: Department of Energy and National Energy Technology Laboratory, 2009.
|
| [6] |
王志刚. 涪陵焦石坝地区页岩气水平井压裂改造实践与认识[J]. 石油与天然气地质, 2014, 35(3): 425-430. WANG Z G. Practice and cognition of shale gas horizontal well fracturing stimulation in Jiaoshiba of fuling area[J]. Oil & Gas Geology, 2014, 35(3): 425-430. |
| [7] |
蒋可.长宁威远区块页岩气水平井固井质量对套管损坏的影响研究[D].成都: 西南石油大学, 2016. JIANG K. Study on the influence of cementing quality of horizontal shale gas wells in Weiyuan area of Changning on casing damage[D]. Chengdu: Southwest Petroleum University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10615-1017038088.htm |
| [8] |
陈朝伟, 石林, 项德贵. 长宁-威远页岩气示范区套管变形机理及对策[J]. 天然气工业, 2016, 36(11): 70-75. CHEN Z W, SHI L, XIANG D G. Mechanism of casing deformation in the Changning-Weiyuan national shale gas project demonstration area and countermeasures[J]. Natural Gas Industry, 2016, 36(11): 70-75. DOI:10.3787/j.issn.1000-0976.2016.11.009 |
| [9] |
田中兰, 石林, 乔磊. 页岩气水平井井筒完整性问题及对策[J]. 天然气工业, 2015, 35(9): 70-76. TIAN Z L, SHI L, QIAO L. The problem of wellhead integrity in shale gas horizontal wells and its countermeasures[J]. Natural Gas Industry, 2015, 35(9): 70-76. DOI:10.3787/j.issn.1000-0976.2015.09.010 |
| [10] |
BRUNO M S, NAKAGAWA F M. Pore pressure influence on tensile fracture propagation in sedimentary rock[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1991, 28(4): 261-273. |
| [11] |
BRUNO M S, NELSON R B. Microstructural analysis of the inelastic behavior of sedimentary rock[J]. Mechanics of Materials, 1991, 12(2): 95-118. DOI:10.1016/0167-6636(91)90057-7 |
| [12] |
SCHWALL G H, DENNEY C A. Subsidence induced casing deformation mechanisms in the Ekofisk field[R]. SPE 28091-MS, 1994.
|
| [13] |
WONG R C K, CHAU K T. Casing Impairment Induced by shear slip along a weak layer in shale due to fluid(steam) injection[J]. Journal of Canadian Petroleum Technology, 2006, 45(12): 60-66. |
| [14] |
高利军, 乔磊, 柳占立, 等. 页岩储层剪切套损的数值模拟及固井对策研究[J]. 石油机械, 2016, 44(10): 6-10. GAO L J, QIAO L, LIU Z L, et al. Numerical modeling and cementing countermeasure analysis of casing shear damage in shale reservoir[J]. China Petroleum Machinery, 2016, 44(10): 6-10. |
| [15] |
刘扬, 何秀清, 王彦兴. 井下套管弯曲变形的数值模拟[J]. 大庆石油学院学报, 2005(5): 39-40, 51, 125. LIU Y, HE X Q, WANG Y X. Numerical simulation of bending deformation of downhole casing[J]. Journal of Daqing Petroleum University, 2005(5): 39-40, 51, 125. |
| [16] |
任思齐, 康志勤, 吕义清. 热采井套管热固耦合作用数值模拟分析[J]. 煤炭技术, 2017, 36(5): 301-303. REN S Q, KANG Z Q, LÜ Y Q. Numerical simulation thermal-stress coupling in casing of thermal recovery wells[J]. Coal Technology, 2017, 36(5): 301-303. |
| [17] |
寇永强.油田开发过程中套管损坏数值模拟研究[D].青岛: 中国石油大学(华东), 2011. KOU Y Q. Numerical simulation study of casing damage during oilfield development[D]. Qingdao: China University of Petroleum, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10425-1014016979.htm |


