2. 华南理工大学机械与汽车工程学院;
3. 中海油研究总院有限责任公司
2. School of Mechanical and Automotive Engineering, South China University of Technology;
3. CNOOC Research Institute Co., Ltd.
0 引言
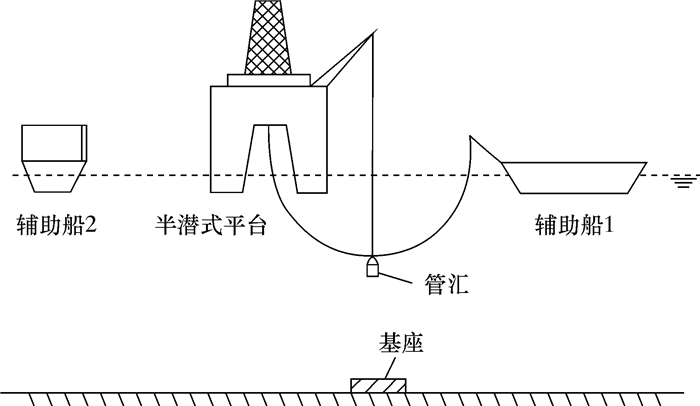
水下滑轮安装法是深水超大型管汇的主要安装方法之一,主要是利用一艘半潜式平台和两艘辅助船只进行水下目标管汇的安装下放。此种方法是传统吊装方法的又一次改进,通过在水下管汇上安装滑轮巧妙地将单根钢丝缆绳的承重变为双根钢丝缆绳共同承载,将钢丝缆绳的载荷减小了1/2,降低了对钢丝缆绳自身承载力、强度以及绞车的能力要求,更有利于深水、超深水大型水下管汇的安装。2002年4月,Petrobras公司首次应用滑轮安装法将尺寸为12 m×7 m×5 m、质量为175 t的水下管汇成功安装在水深为1 885 m的巴西P-52油田[1-7]。
目前,国内外学者对水下管汇安装下放的研究多集中在传统的钻杆或钢丝缆绳吊装下放上。Y.BAI等[8]介绍了一种由钻杆下放安装水下丛式管汇的三维力学分析方法,并在小变形弯曲理论的基础上,通过有限元离散法推导出钻杆的位移、轴向拉伸、弯矩和倾角的理论公式,同时与OrcaFlex的仿真模拟结果进行了比较。付剑波等[9]提出在综合考虑安全性和可靠性的前提下管汇安装方法的选择原则,分析了采用月池法进行传统水下管汇吊装过程。王莹莹等[10]利用OrcaFlex研究了海流和波浪环境下1 500 m水深的采油树利用钻杆安装工艺中钻杆的受力情况,并计算了钻杆横向位移,分析得出钻杆顶端部分属于最危险部分。汤珂[11]利用FLUENT软件建立了1 500 m管汇的水动力计算模型,求得管汇非惯性水动力系数,并分析了管汇水动力系数的影响因素以及下放过程不同状态下的水动力系数取值方法,但是并没有考虑管汇与船舶的耦合作用。笔者以滑轮安装法中的钢丝绳为分析对象,在不考虑环境载荷的影响下,对水下管汇下放过程中钢丝绳的最大拉力以及曲线形状进行了分析,并研究了水深和管汇质量对其的影响。所得结论有助于确保滑轮法安装中钢丝绳的安全使用,并可作为研究各种非线性及动力影响的初始出发点。
1 滑轮法安装过程的理论分析水下管汇安装过程受到很多因素的影响,比如下放经过飞溅区时会受到风、浪、流等环境载荷的作用,这些影响非常复杂。笔者选定的气候窗为微风、微浪及无海流情况,因而分析中不考虑风、浪、流的影响,而且假定安装过程很缓慢,不考虑惯性的影响,即只考虑准静力过程。
1.1 空中阶段钢丝绳的静力分析利用吊机开始下放时,水下管汇完全由吊机缆绳悬吊着,穿过滑轮的钢丝绳对水下管汇不起承重作用。系统简化示意图如图 1所示。
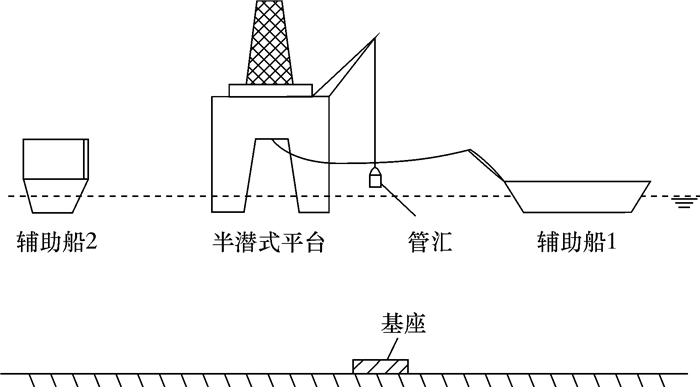
|
| 图 1 系统简化示意图 Fig.1 Schematic of installation system |
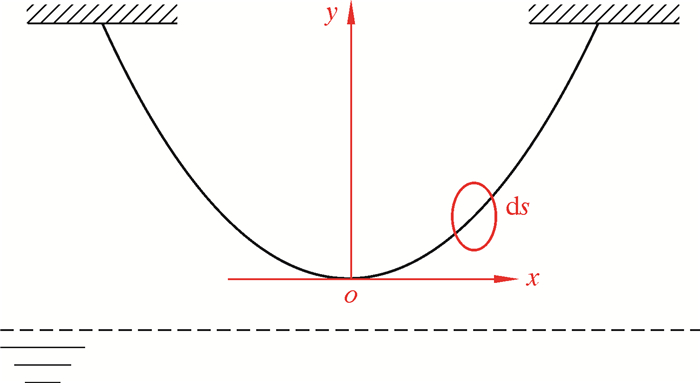
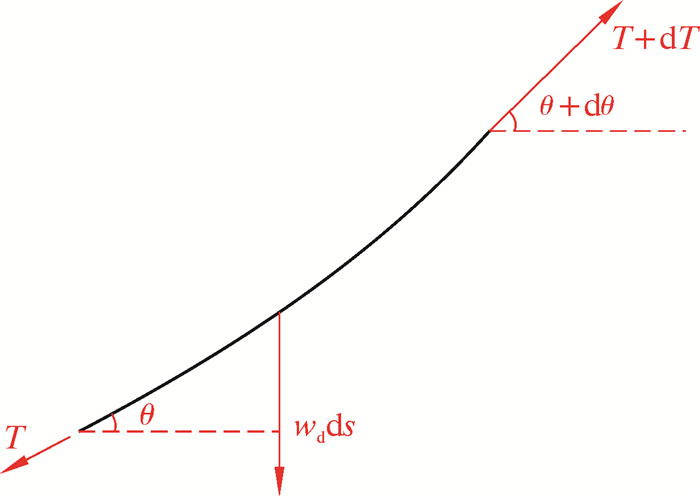
假定钢丝绳在半潜式平台和辅助船1的悬挂点高度一致,并且为固定约束端。以钢丝绳的最低点作为坐标原点,建立如图 2所示的坐标系。取微元段ds为研究对象,其受力情况如图 3所示。作用在钢丝绳上的载荷为拉力T和T+dT以及钢丝绳的干重wdds。T为空中阶段钢丝绳的拉力。由微元段在切线和法线方向上的平衡方程可得:
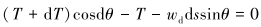
|
(1) |
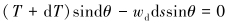
|
(2) |
|
| 图 2 钢丝绳在空中简化模型 Fig.2 Simplified model for wire rope in the air |
|
| 图 3 空中阶段钢丝绳微元段ds受力图 Fig.3 Forces on the wire rope micro-element ds |
图 3中θ是钢丝绳与水平方向的夹角。由于dθ为微量,所以sindθ≈dθ,cosdθ≈1,dTdθ≈0。微元段的几何关系为dx=dscosθ,dy=dssinθ。化简式(1)和式(2)得到:
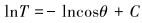
|
(3) |
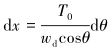
|
(4) |
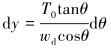
|
(5) |
对两端同时积分,得到拉力方程和形状方程。T0为空中阶段钢丝绳的初始水平拉力,为未知常数。
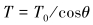
|
(6) |
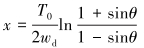
|
(7) |
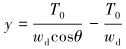
|
(8) |
下放管汇通过飞溅区时,仍然由吊机缆绳承受管汇的全部重力,穿过滑轮的钢丝绳不起承重作用。但与空中阶段不同的是:钢丝绳的一部分会随着管汇的下放而浸没到海水中,而另一部分仍然呈现在空气中,如图 4所示。
|
| 图 4 钢丝绳入水初期(吊机未断开连接)示意图 Fig.4 Schematic diagram of the initial entry of the wire rope into the water(the crane is not disconnected) |
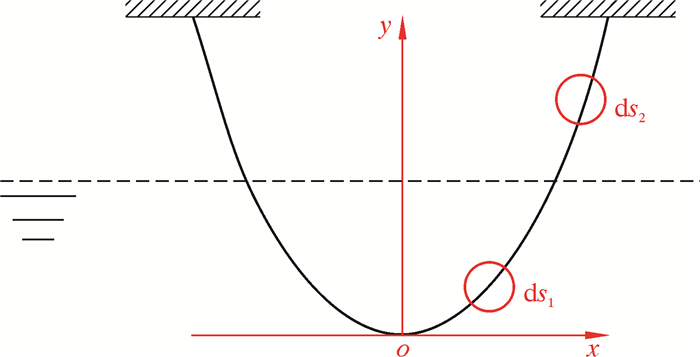
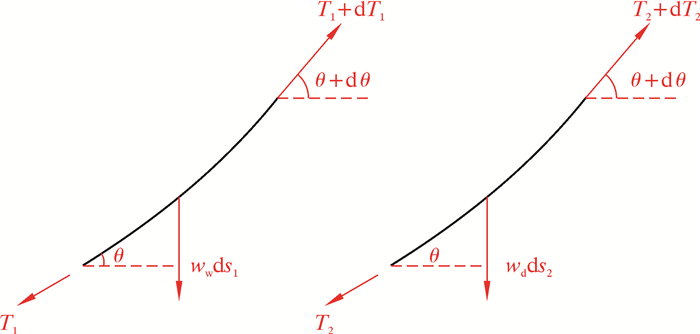
由于两部分钢丝绳的单位长度重力不同,应分为水上和水下两部分研究。以钢丝绳最低点为坐标原点建立坐标系,如图 5所示。分别截取钢丝绳水中微元段ds1和空中微元段ds2,其对应的受力如图 6所示。图 6中:ww为钢丝绳的单位长度湿重,T1为浸没在海水中的钢丝绳上的拉力,T2为未浸未在海水中的钢丝绳上的拉力。
|
| 图 5 钢丝绳入水初期简化模型 Fig.5 Simplified model of the initial entry of the wire rope into water |
|
| 图 6 钢丝绳在入水初期微元段受力图 Fig.6 Schematic diagram of the forces on the wire rope micro-element in the initial stage of water entry |
沿切线和法线方向建立水中钢丝绳的平衡方程并化简,得到其拉力方程和形状方程:
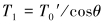
|
(9) |
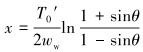
|
(10) |
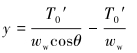
|
(11) |
由平衡方程可得空气中钢丝绳段的拉力方程:
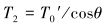
|
(12) |
式中:T0′为钢丝绳部分入水且管汇与吊机缆绳未断开阶段钢丝绳上的初始水平拉力。
两段钢丝绳在水面处拉力和转角应相等、位移应连续,于是有:
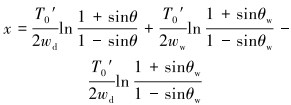
|
(13) |
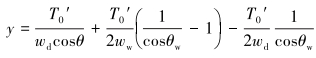
|
(14) |
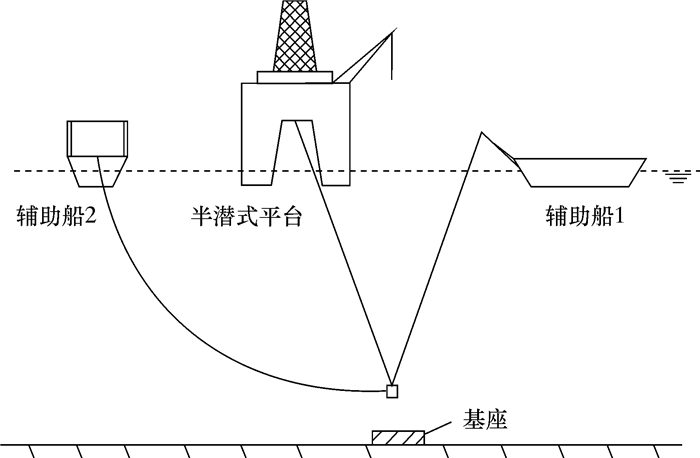
水下管汇下放经过飞溅区到达水下一定位置处,断开吊机缆绳与管汇的连接,由穿过滑轮的钢丝绳承担水下管汇的全部重力,完成后续的下放工作,如图 7所示。
|
| 图 7 钢丝绳入水后示意图 Fig.7 Schematic diagram of the wire rope after entering the water |
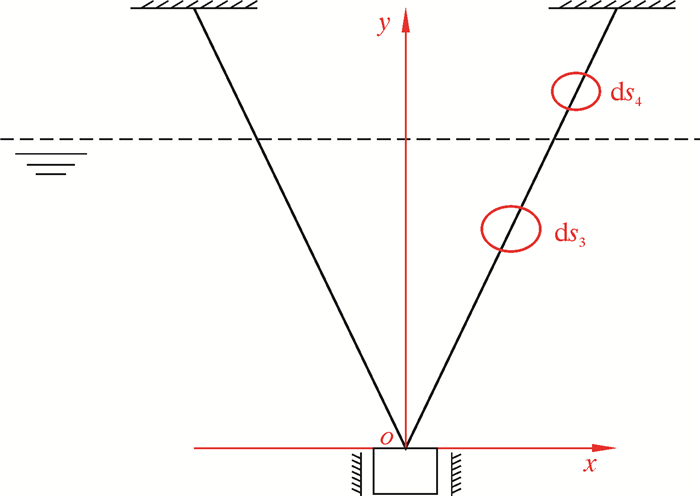
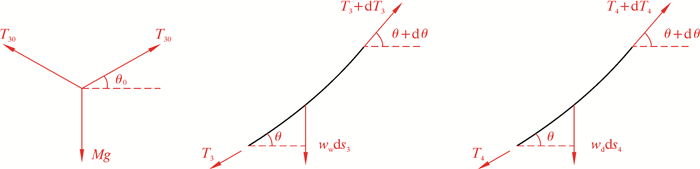
在管汇下放过程中,与辅助船2连接的钢丝绳作为安装过程中的辅助钢丝绳,能避免管汇发生扭转,使管汇能够垂直下放,到达预定安装区域。由于辅助钢丝绳不影响管汇垂直方向的运动和受力,故不考虑其受力。以连接点为坐标原点建立坐标系,简化后的模型如图 8所示。分别以滑轮、水中微元段ds3和空中微元段ds4为研究对象,其对应的受力如图 9所示。图 9中T30为管汇与吊机缆绳断开阶段钢丝绳上的初始拉力,T3为该阶段浸没在海水中钢丝绳上的拉力,T4为该阶段未浸没在海水中钢丝绳上的拉力,T0″为该阶段钢丝绳的初始拉力。
|
| 图 8 钢丝绳入水后的简化模型 Fig.8 Simplified model of the wire rope after entering the water |
|
| 图 9 钢丝绳入水后微元段受力图 Fig.9 Forces on the micro-element of the wire rope after entering the water |
由滑轮垂直和水平方向的平衡条件可得:
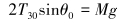
|
(15) |
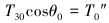
|
(16) |
由此得到:
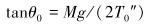
|
(17) |
式中:M为悬重的质量,g为重力加速度。
对微元段ds3和微元段ds4进行受力分析,可得钢丝绳水中部分的拉力方程和形状方程为:
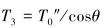
|
(18) |
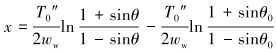
|
(19) |
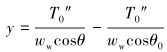
|
(20) |
利用水面处的连续条件,可得到钢丝绳在空气中的拉力方程和形状方程。
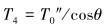
|
(21) |
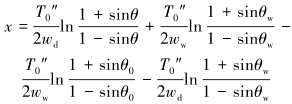
|
(22) |
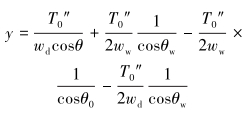
|
(23) |
假定半潜式平台的悬挂点和辅助船1的悬挂点之间距离为100 m,管汇位于两者中间,距两悬挂点均为50 m。两悬挂点距离水平面的高度均为20 m。钢丝绳单位长度干重wd=329.8 N/m,单位长度湿重ww=206.5 N/m。并假定在水下50 m的位置断开管汇与吊机缆绳的连接。
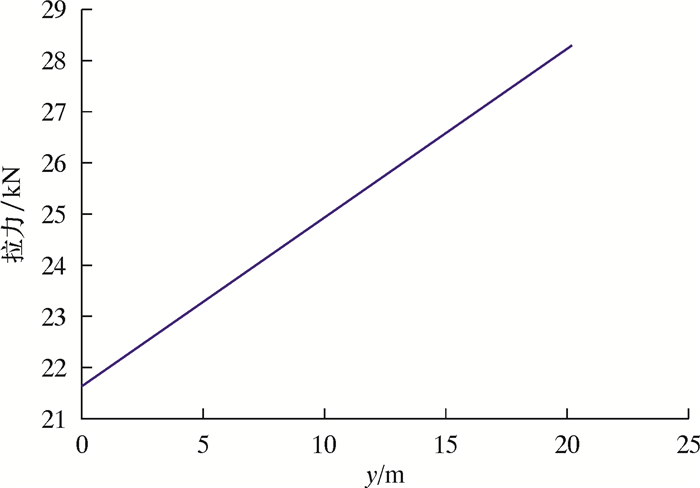
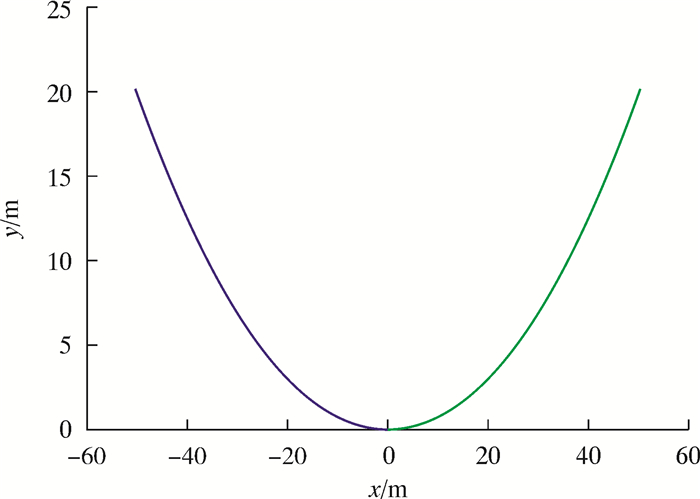
2.1 钢丝绳全部在空中阶段根据式(6)~式(8)可得钢丝绳上每一点所受的拉力及位置坐标,从而可得拉力随位置变化的曲线以及钢丝绳的形状曲线,分别如图 10和图 11所示。由图 10可以看到,在悬挂高度为20 m时,钢丝绳上的拉力随着y的增加而不断增大,在最高点即与辅助船1以及半潜式平台的悬挂点处拉力最大,故此处的应力最大,为最危险的地方。图 11描述了钢丝绳在其自身重力作用下而自然下垂的悬链线形状。
|
| 图 10 高20 m钢丝绳各点所受的拉力图 Fig.10 Tension of the wire rope with the height of 20 m |
|
| 图 11 高20 m钢丝绳的悬链线图 Fig.11 Catenary diagram of the wire rope with the height of 20 m |
2.2 钢丝绳部分入水但未承受管汇重力阶段
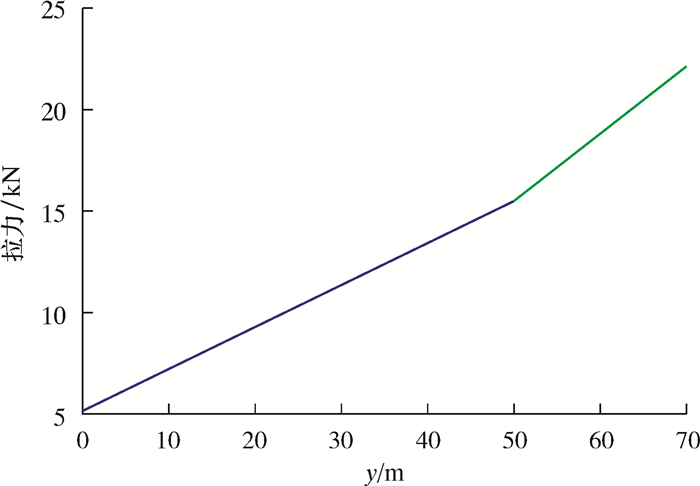
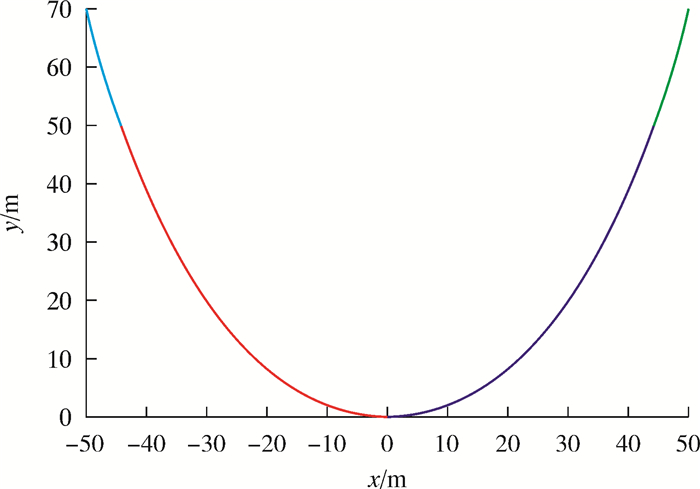
此阶段选取水深50 m作为计算条件,则钢丝绳的悬挂高度为70 m。利用式(9)~式(14),用迭代法得到系统的初始水平拉力T0′,然后可绘出钢丝绳各点的拉力和两段钢丝绳的形状曲线,如图 12和图 13所示。
|
| 图 12 高70 m钢丝绳各悬点的拉力图 Fig.12 Tension of the wire rope with the height of 70 m |
|
| 图 13 高70 m钢丝绳的悬链线图 Fig.13 Catenary diagram of the wire rope with the height of 70 m |
由图 12可以看到,钢丝绳垂向高度为70 m时,由于钢丝绳在空中和在水中的单位长度重力不同,钢丝绳的拉力在水面处以另一斜率增加,但是总体上钢丝绳的拉力随着y的增加而不断增大,所以在最高点即与辅助船1以及半潜式平台的悬挂点处拉力最大,故此处的应力最大,是最危险的地方。图 13描述了钢丝绳在其自身重力作用下而下垂的悬链线形状,由于钢丝绳的干重与湿重不同,钢丝绳由两段不同的悬链线组成。
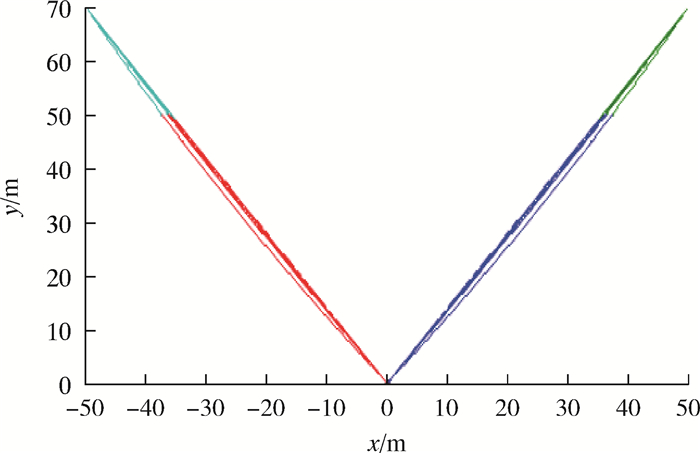
2.3 钢丝绳承受管汇全部重力阶段分析吊机缆绳与水下管汇断开、钢丝绳完全承担管汇重力的情况,钢丝绳的高度为70 m。由于管汇重力不同,式(15)~式(23)的解不同。利用迭代法首先确定出系统拉力的水平分量(常数),然后可确定各段钢丝绳的拉力和位置坐标,进而可绘出钢丝绳的拉力和形状图。图 14为悬挂重力100、300、500、1 000、2 000和3 000 kN时水下管汇的钢丝绳形状图。由于不同悬重的钢丝绳形状曲线部分重合,图 14没有指出具体的悬重指示。
|
| 图 14 不同悬挂时水下管汇的钢丝绳形状图 Fig.14 Shapes of the wire rope with different subsea manifolds |
从图 14可以看到,钢丝绳在水深50 m、悬挂重力为100、300、500、1 000、2 000和3 000 kN的水下管汇时,其形状都是由两段不同的曲线组成,这些钢丝绳的形状略微不同,且可近似为直线。
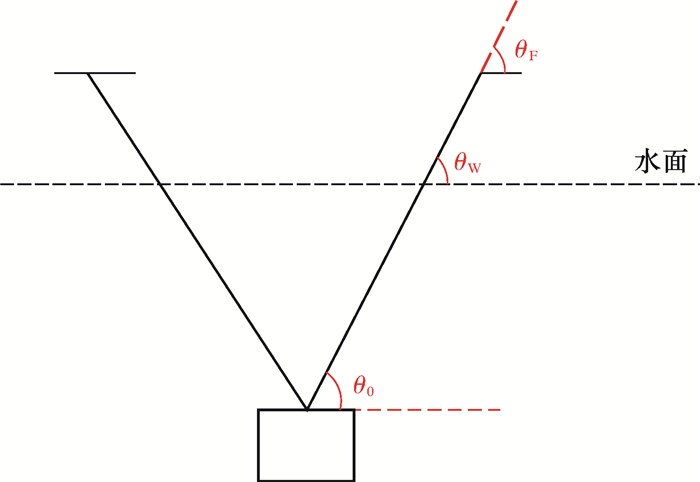
不同重力的管汇在水深50 m时钢丝绳上一些点的切线与水平轴的夹角计算值如表 1所示。其中,起始点指钢丝绳与滑轮的切点。此外,连接滑轮与悬挂点的直线倾角α=56.46°。
| 管汇重力/ kN |
θ0(起始点)/ (°) |
θw(水面点)/ (°) |
θF(悬挂点)/ (°) |
| 100 | 49.82 | 56.24 | 59.31 |
| 300 | 52.81 | 55.08 | 56.38 |
| 500 | 53.46 | 54.83 | 55.66 |
| 1 000 | 53.95 | 54.65 | 55.07 |
| 2 000 | 54.21 | 54.56 | 54.77 |
| 3 000 | 54.29 | 54.52 | 54.67 |
各角度的含义如图 15所示。
|
| 图 15 各角度示意图 Fig.15 Schematic diagram of wire rope angle |
由表 1可知,在管汇重力一定时,钢丝绳自起始点至水面点再到悬挂点的角度单调增加;随着管汇重力的增加,起始点的角度θ0单调增加,而水面点和悬挂点的角度θw和θF都单调减小,因此θF与θ0的差值也单调减小,θF与θ0的值越来越趋近α,这意味着钢丝绳的形状越来越接近一条直线。
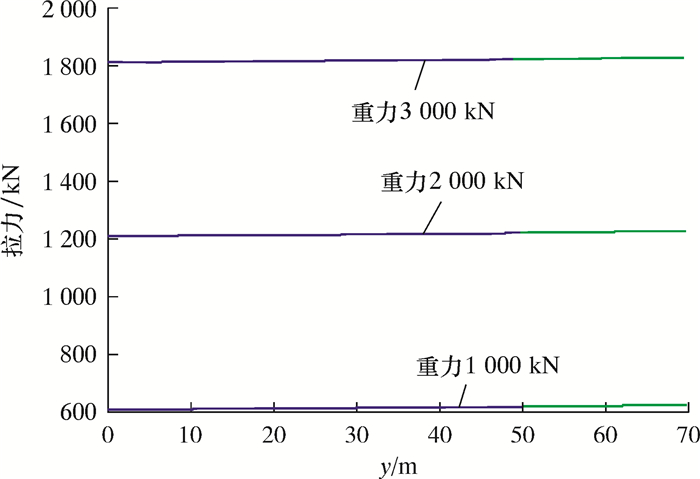
图 16为不同管汇重力下y与拉力的关系图。由图 16可以看到,随着管汇重力的增大,钢丝绳受到的拉力也增大,并且近似以管汇重力的倍数增大。在同一管汇重力下,钢丝绳受到的拉力随着y的增大而略微增大,而且与水中相比,空气中钢丝绳受到的拉力增大速率更大,同时还可以看出悬挂点处受到的拉力最大,故此处应力最大。
|
| 图 16 高70 m钢丝绳悬挂重力不同的水下管汇时的拉力图 Fig.16 Tensile of the wire rope with the height of 70 m when hanging different gravity manifolds |
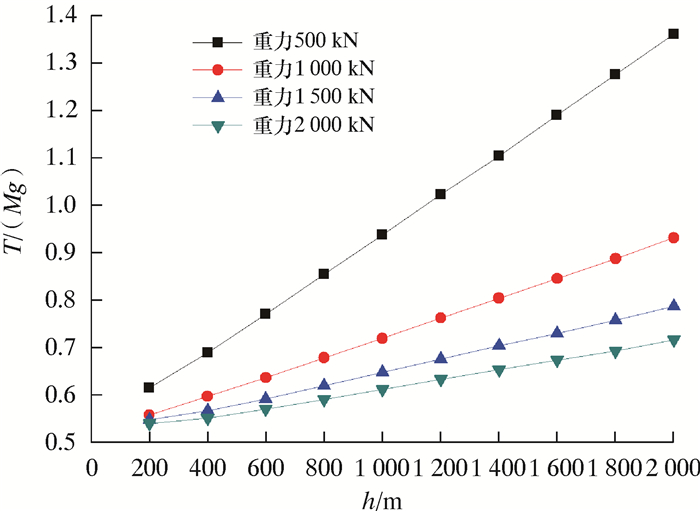
最大拉力发生在钢丝绳悬挂点(最高点),利用MATLAB得到悬挂点的拉力值,再通过Origin软件绘制出悬挂点拉力与水深和管汇重力的关系图。钢丝绳悬挂点的拉力与管汇重力比值T/(Mg)与水深h的关系曲线如图 17所示。
|
| 图 17 钢丝绳悬挂点T/(Mg)与水深h的关系图 Fig.17 Relationship between wire rope suspension point T/(Mg) and water depth h |
由图 17可以看到,随着水深的增加,钢丝绳的拉力(Mg是固定值)单调增大,并且近似线性增加;在同一水深,管汇重力越大,钢丝绳的T/(Mg)越小,说明钢丝绳重力对拉力的影响越小。
图 18展示了在水深分别为500、1 000、1 500和2 000 m时钢丝绳悬挂点的拉力与管汇重力的关系。由图 18可以看到,随着管汇重力的增大,钢丝绳的T/(Mg)单调减小;对于同一管汇重力,随着水深的增加,悬挂点的拉力不断增加,钢丝绳重力对拉力的影响增大。原因是:管汇重力一定时,Mg是常数,随着水深的增加,T/(Mg)增大,因此拉力也增大;同时,随着水深的增加,钢丝绳长度在不断增加,钢丝绳本身的重力也在增大,说明钢丝绳拉力的增大是由于钢丝绳本身重力引起的。
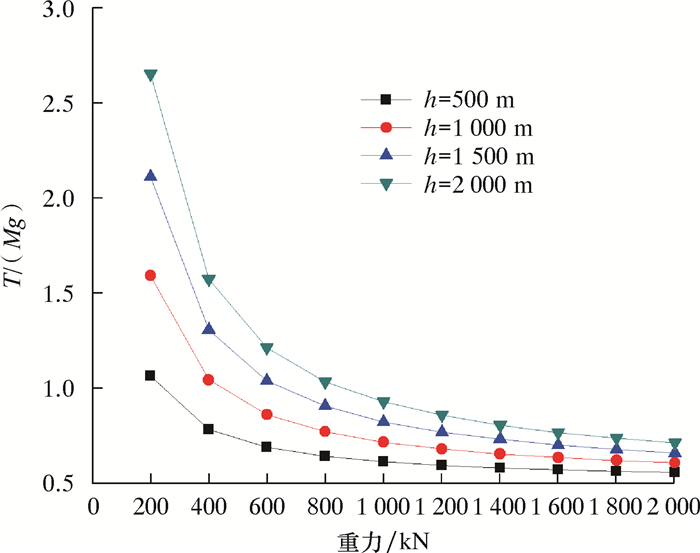
|
| 图 18 水下管汇重力与钢丝绳悬挂点T/(Mg)的关系图 Fig.18 Relationship between subsea manifold gravity and wire rope suspension point T/(Mg) |
3 结论
(1) 滑轮法下放管汇的所有阶段中,钢丝绳受到的拉力均与该点切线与水平轴夹角的余弦成反比;对于给定的水深,钢丝绳任意点拉力的水平分量为常数,该常数随水深的不同而变化。
(2) 钢丝绳受到的拉力随着高度增加而逐渐增大,由于钢丝绳的湿重小于干重,拉力随高度的增加在空气中比在水中增加速率大。在第三阶段,最高悬挂点受到的拉力随着水深增加而近似呈线性增加,同时也随着水下管汇重力的增加而增大。
(3) 钢丝绳的形状由其单位长度重力和管汇重力决定,进入水中后,其形状曲线都由两段不同的曲线组成。钢丝绳承担水下管汇重力阶段,其两段形状曲线随着管汇重力的增加越来越趋近一条直线。
| [1] |
CHRISTIAN C, DENBY M, HUGO C, et al. Progression of ultradeep subsea deployment systems[R]. OTC 15147-MS, 2003.
|
| [2] |
STOCK P F K, CERQUEIRA M B, ROVERI F E, et al. A new method for deploying subsea hardware in deep water[C]//Proceedings of the 2002 Deep Offshore Technology, New Orleans, USA, DOT 2002.
|
| [3] |
张瑾, 谢毅. 深水水下管汇安装方法研究与进展[J]. 海洋工程, 2011, 29(1): 143-148. ZHANG J, XIE Y. Research and development of subsea manifold installation methods[J]. The Ocean Engineering, 2011, 29(1): 143-148. DOI:10.3969/j.issn.1005-9865.2011.01.022 |
| [4] |
姚丽琳.深水水下安装下放运动分析技术研究[D].上海: 上海交通大学, 2011. YAO L L. Research on hydrodynamic analysis of subsea deepwater installation[D]. Shanghai: Shanghai Jiao Tong University, 2011. |
| [5] |
WANG A M, ZHU S, ZHU X, et al. Pendulous installation method and its installation analysis for a deepwater manifold in South China Sea[J]. International Society of Offshore and Polar Engineers, 2013(23): 774-784. |
| [6] |
JOSE M L, MARIELE L K, PAULO F S, et al. Development of subsea facilities in the Roncador Field(P-52)[R]. OTC 19274-MS, 2008.
|
| [7] |
王莹莹, 段梦兰, 冯玮, 等. 深水管汇的安装方法及其在南海荔湾3-1气田中应用研究[J]. 海洋工程, 2011, 29(3): 23-30. WANG Y Y, DUAN M L, FENG W, et al. Investigation on installation methods of deepwater manifolds and their applications to LW3-1 gas filed in South China Sea[J]. The Ocean Engineering, 2011, 29(3): 23-30. DOI:10.3969/j.issn.1005-9865.2011.03.003 |
| [8] |
BAI Y, RUAN W D, YUAN S, et al. 3D mechanical analysis of subsea manifold installation by drill pipe in deep water[J]. Ship and Offshore Structures, 2014, 9(3): 333-343. DOI:10.1080/17445302.2013.783538 |
| [9] |
付剑波, 苏锋, 张凡, 等. 海洋石油管汇安装方法及安装过程力学分析[J]. 石油矿场机械, 2014, 43(4): 22-25. FU J B, SU F, ZHANG F, et al. Selection mthod and mchanical analysis on subsea manifold installation[J]. Oil Filed Equipment, 2014, 43(4): 22-25. DOI:10.3969/j.issn.1001-3482.2014.04.005 |
| [10] |
WANG Y Y, TUO H H, LI L W, et al. Dynamic simulation of installation of the subsea cluster manifold by drilling pipe in deep water based on OrcaFlex[J]. Journal of Petroleum Science and Engineering, 2018, 163: 67-78. DOI:10.1016/j.petrol.2017.12.049 |
| [11] |
汤珂.深水滑轮法下放管汇过程的多体动力学研究[D].北京: 中国石油大学(北京), 2014. TANG K. Study on dynamics of subsea manifold pulley method installation system[D]. Beijing: China University of Petroleum(Beijing), 2014. |


