2. 中国石油长庆油田分公司第八采油厂
2. The Eighth Oil Production Plant of PetroChina Changqing Oilfield Company
0 引言
为了减轻振动、提高底部钻具组合(Bottomhole Assembly,以下简称BHA)可靠性、缩短非生产时间,钻井工作者一直致力于钻井振动的研究[1-3]。自开展试验研究以来[4],研究方法不断增多,包括常微分方程、偏微分方程、有限元建模、信号处理、数据分析乃至神经网络[5]。实质上,钻井振动常常分为轴向振动[6]、扭转振动[7]和侧向振动[8-9]3种类型,但这3种振动常常同时发生,且可以互相作为激励源[10]。反向涡动是侧向振动的极端情况,进一步了解反向涡动现象及其对井下工具的有害影响极为必要。然而,由于井下测量限制,研究仅限于黏滑和钻头跳动等低频现象(通常低于50 Hz)[11-15]。测量装置的技术进步不仅增强了理解钻头和BHA动态特性的能力[16-17],而且还可进行高频扭转振荡等高频动态现象研究[18-22]。因此,迫切需要更高的频率和高幅值测量,以量化和了解恶劣的井下环境。
为了解释反向涡动过程中的振动响应,分析动态载荷的更高频率(>100 Hz),反向涡动试验机得到了研发,其可容纳一个或多个串联的全尺寸BHA工具,旋转BHA可引起反向涡动。该试验机能够模拟光滑和不连续井眼环境下的反向涡动响应。ϕ171.45 mm BHA在ϕ215.9 mm井眼中的试验结果表明,光滑井眼和不连续井眼的振动幅值和频率不同,特别是不连续井眼的激发频率高达200 Hz。为了进行更深入的研究,贝克休斯和莱斯大学的研究人员开发了解析模型和有限元模型,解析模型简单、计算快速,但仅局限于光滑井眼。有限元模型克服了解析模型的缺陷,涉及不连续井眼模拟。试验结果验证了解析模型和有限元模型的预测精度和有效性。为了给我国的钻井工作者提供借鉴,推动我国钻井动力学分析技术的发展,笔者对研究情况进行了介绍。
1 反向涡动试验机反向涡动试验机主要由BHA、传动马达、安全环、水平配置中支撑BHA的轴承和沿BHA长度安置的减震环组成(见图 1)。圆柱形滚珠轴承位于BHA两端,可防止侧向偏转,但允许自由旋转。每个轴承与末端轴配对,末端轴用作适配器,当安装不同的BHA时,末端轴保持不变。传动轴配备有锁紧组件,防止轴向运动。尾轴呈现机械碾压表面,当BHA偏转时,允许BHA通过轴承轴向运动。传动带连接传动马达至BHA,灵活性强,当BHA旋转时,可实现平移和旋转。传动马达功率为55 kW,BHA转速为0~300 r/min。轴承和传动马达安装在地基中水泥固定的钢架上,因此可调整轴承之间的距离,以适应各种BHA长度。如果BHA破裂,安全环可避免意外事故。

|
| 1—传动马达;2—轴承;3—传动轴;4—BHA;5—安全环;6—减震环。 图 1 反向涡动试验机 Fig.1 Backward whirl testing machine |
试验准备过程中,用钢筋间隔件升高轴承,直至BHA中心接近减震环中心线(升高BHA极为必要,这是因为如果初始接触压力太高,工具不会进入反向涡动状态)。为了获得反向涡动过程中的动态数据,将两个三轴加速度计安装在靠接减震环的BHA的外表面。传感器与NI数据采集系统进行通信,采样频率为2 500 Hz。在试验开始时,马达驱动BHA转速为60 r/min。当BHA旋转时,由于沿BHA直径的质量不平衡和各向异性刚度,BHA径向偏移增大。当径向偏移超过BHA和减震环之间的间隙时会发生撞击,如果摩擦足够大,撞击导致自激反向涡动,并记录加速度。这些时间记录说明了反向涡动过程中的载荷幅值和频率。在固定的坐标参考系中对加速度进行处理,从而在频域内识别出反向涡动频率[23-24]。
2 模拟研究 2.1 解析模型为简化计算,首先开发了简单的集中参数模型作为最基本模型,以评价试验机中的反向涡动(见图 2)。集中参数模型是基于著名的Jeffcott转子模型的二自由度涡动模型(见图 3)。

|
| 图 2 反向涡动试验机原理图 Fig.2 Schematic diagram of the backward whirl testing machine |

|
| 图 3 集中参数模型原理图 Fig.3 Schematic diagram of the centralized parameter model |
修正Jeffcott模型[25]使用两个非线性微分方程描述偏心(e)于转子中心(C)的转子质量(G)的偏移。该方程组包含重力(FG)、质量不平衡力(FC)、阻尼(FD)和摩擦接触效应。径向恢复力(FR)由BHA远离井眼中心线的偏转引起。模型的显著特征是包括径向接触力(FN)和切向摩擦力(FT)的非线性接触力。另外,假设转速保持不变,表明不包含扭转自由度(即$φ$=ωt)。考虑到转子运动,极坐标下的二阶微分方程表示为:
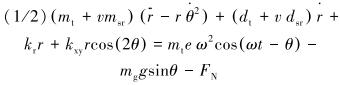
|
(1) |

|
(2) |
式中:FG=mgg,FC=mteω2,FD=(dt+vdsr)



| 变量 | 描述 | 数值 |
| mt | BHA质量/kg | 2.401 4×103 |
| msr | 减震环外壳质量/kg | 450 |
| mg | 重力对质量的影响/kg | 1.500 9×103 |
| kr | 径向刚度/(N·m-1) | 1.915 6×105 |
| kxy | 切向刚度/(N·m-1) | 0 |
| ksr | 减震环刚度/(N·m-1) | 4×108 |
| dt | BHA阻尼系数/(N·s) | 857.9 |
| dsr | 减震环阻尼系数/(N·s) | 1.697 1×104 |
| db | 切向阻尼系数/(N·s) | 100 |
| e | 偏心距/m | 0.02 |
| c0 | 间隙/m | 0.019 |
| rt | BHA外径/m | 0.089 |
| μ | 摩擦因数 | 0.7 |
| ω | BHA转速/(rad·s-1) | 6.82 |
| g | 重力加速度/(m·s-2) | 9.81 |
| v | 逻辑算子 | 0,1 |
| t | 时间/s | 0~5 |
| r | 径向偏移/m | — |
 |
径向速度/(m·s-1) | — |
 |
径向加速度/(m·s-2) | — |
| θ | 角度偏移/rad | — |
 |
角速度/(rad·s-1) | — |
 |
角加速度/(rad·s-2) | — |
方程参数通过采用假设模态法确定,从中利用假设形态函数发现有效质量和刚度。就这一点而言,假设BHA为两个轴承之间的简单支撑梁,同时假设BHA保持第一振动模式,这些假设导致由正弦曲线表示的形状函数。模型包含两个表面之间的干摩擦接触,假设为钢,摩擦因数可能达到0.74,因此模型选择0.7的适当值。保持转速60 r/min不变模拟5 s,用显式四阶龙格库塔法作为数值解法。从侧向加速度的角度对模拟结果进行了讨论。根据为井下测量建立的方法对侧向加速度进行了测量和处理[23]。从时域角度对加速度进行解释,并在频域内识别出优势频率,包括反向涡动频率。模拟得到的侧向加速度记录如图 4所示,可以看出,在模拟的前4 s过程中存在反向涡动。反向涡动过程中,BHA侧向加速度在±1.7g之间变化。

|
| 图 4 集中参数模型侧向加速度记录和相应功率谱 Fig.4 The lateral acceleration record and corresponding power spectrum of centralized parametric model |
为了说明信号的频率,对侧向加速度记录的功率谱进行了计算,显示频率略高,并识别出优势频率为4.70 Hz,相当于反向涡动频率(见图 4)。本质上,反向涡动频率取决于转数及BHA直径与BHA和井眼之间间隙的比值。反向涡动频率运动表示法表示为:

|
(3) |
式中:ωBW为反向涡动频率,Hz;ωBHA为BHA转速,r/min;dSR为减震环直径,m;dBHA为BHA直径,m。
结合表 1中的参数及60 r/min的转速,得到运动学解为4.70 Hz,与解析模型计算的频率完全一致,证实该模型可准确地测量反向涡动过程中的运动响应。利用侧向加速度记录计算得到均方根值为1.19g(见图 4)。工具的运动轨迹如图 5所示。很明显,BHA在一定条件下出现反向涡动。另外,图 5还显示,BHA易于与井壁失去接触(4~5 s),这是当接近井眼顶点时由超过离心力的重力和径向恢复力引起的。因此,在较高的转速下,离心力较大,BHA保持与井壁接触。

|
| 图 5 解析集中参数模型轨迹 Fig.5 Trajectory of analyzing the centralized parameter model |
显然,由于诸多假设,简单的集中参数模型可能降低预测精度,其局限性主要体现在:①集中质量假设,只能捕获BHA完整惯性;②假设面面接触为单点接触,而面面接触影响法向接触力和切向摩擦力;③未考虑轴承中心和井眼中心之间的偏移,并忽略轴的各向异性刚度特性;④井眼不连续性过于复杂,集中参数模型未能涉及。尽管解析模型存在诸多局限性,但仍然准确预测了反向涡动特性,并与动态涡动频率解一致。该模型的另一个优势是计算效率高,在PC机上几秒钟内即可完成计算[24]。
2.2 2D有限元模型有限元模型可克服解析模型的局限性,2D有限元模型的开发目的是提供最基本和快速的解决方案,几何结构包括减震环的横截面和BHA的横截面(见图 6)。BHA的有效质量被固定到模型几何体上,作为点质量,偏心距为20 mm。安装在BHA上的弹簧提供了径向恢复力。BHA长度远大于直径,因此假设为平面应变,轴向方向应变为0。施加位移至减震环,以说明轴承和减震环之间的偏移。施加重力加速度至整个系统,设定BHA转速为60 r/min。

|
| 图 6 2D有限元模型(光滑减震环) Fig.6 2D finite element model(smooth shock absorbing ring) |
模拟包括两个加载步骤,第一个加载步骤为向系统施加重力,并包括减震环的静态位移。减震环76.2 mm的位移用于匹配物理试验偏移。模拟过程中求得静态位移解,偏移的BHA靠近减震环中心。在第一个加载步骤完成后,实施第二个步骤,即在BHA上施加60 r/min的转速。在5 s的模拟时间内,完成了瞬态模型求解,侧向加速度结果见图 7。

|
| 图 7 2D有限元模型侧向加速度记录和相应功率谱(光滑减震环) Fig.7 The lateral acceleration record and corresponding power spectrum of the 2D finite element model(smooth shock absorbing ring) |
由于质量不平衡,BHA振荡远离静态位移的初始位置,并与减震环接触(0~1 s)。由于摩擦接触,1 s后出现反向涡动。一旦进入稳态反向涡动,侧向加速度在±1.8g之间变化,这与解析解一致。功率谱表明,优势反向涡动频率为4.73 Hz,较高的频率再次被忽略。此外,计算得到信号的均方根值为1.21g。所有解的特性与解析模型匹配,反向涡动频率与式(3)中的运动学解一致,表明偏移对稳态反向涡动响应的影响微不足道。另外,对于光滑减震环反向涡动的起始、反向涡动频率和反向涡动幅值的预测,解析模型足以代替2D有限元模型。
前面的模型假设减震环完全光滑,而实际情况并非如此。图 8中的2D有限元模型研究了减震环中有切口的不连续井眼,加载步骤与2D光滑减震环模型相同。

|
| 图 8 2D有限元模型(不连续减震环) Fig.8 2D finite element model(discontinuous shock absorbing ring) |
侧向加速度记录表明,反向涡动再次出现,但井眼不连续性的存在,使BHA涡动频率更加不规律(见图 9)。由于BHA突然撞击切口和减震环壁,加速度幅值增大,加速度峰值介于20g~30g之间。观察功率谱发现,反向涡动频率为9.50 Hz,与运动学解不一致,这是因为不连续干扰了BHA的运动轨迹,导致与减震环壁失去接触。因此,与光滑减震环相比,涡动频率更高。信号中存在两个明显的峰值,第一个峰值与9.50 Hz的涡动频率相关,第二个峰值与19 Hz的涡动频率相关,这是BHA和井壁及切口的接触引起的。另外,不连续的存在激发了更大的频率范围,在40~50 Hz和60~80 Hz之间尤为明显,100 Hz以上的频率仍然忽略不计。加速度记录均方根值为6.79g,远高于光滑减震环1.21g的均方根值。图 10进一步说明了光滑和不连续减震环中BHA的特性。很明显,在光滑减震环中,一旦出现涡动,BHA保持反向涡动特性。与此相反,在不连续减震环的轨迹图中观察到三角涡动模式,BHA周期性地与减震环壁失去接触。

|
| 图 9 2D有限元模型侧向加速度记录和相应功率谱(不连续减震环) Fig.9 The lateral acceleration record and corresponding power spectrum of the 2D finite element model (discontinuous shock absorbing ring) |

|
| 图 10 2D有限元模型轨迹图 Fig.10 2D finite element model trajectory |
2D有限元模型存在一些局限性,体现在:①假设集中质量代表BHA惯性,而质量实际上是沿BHA长度分布的;②对于BHA的径向恢复力,固定弹簧过于理想化;③在所有方向,假设减震环接触刚度不变,但是由于存在基础刚度,真实减震环外壳在垂直方向上呈现较高的刚度;④在2D模型中假设线线接触,不能准确地捕获面面接触特性;⑤忽略弯曲刚度的各向异性,假设激发仅源于质量不平衡。2D模型模拟时间不到1 h[24]。
2.3 3D有限元模型全3D实体模型(见图 11)开发的目的是克服解析模型和2D有限元模型的所有局限性,能够精确地分析系统物理学特征。假设BHA为均匀横截面的圆柱梁,外径和内径分别为178和55 mm。50 kg的偏心质量固定于减震环中部的BHA,与BHA中心轴线相距20 mm。因为对整个梁的几何结构进行了建模,BHA惯性完全得到了利用。同时对整个减震环外壳进行了建模,以解释水平和垂直方向上的刚度差。因此,固定外壳底面以代表基础刚度,而外壳的其他面不受约束。零位移和自由旋转定义为轴承位置的边界条件,描述了简单的支持约束(见图 12)。此外,尾轴承位置轴向偏转完全自由,以适应无力矩产生的轴承之间的梁的偏转。在传动带所在的BHA表面定义了转速(见图 13)。传动带弹性好,在BHA上不提供明显的力或力矩,因此在施加转速的位置允许自由旋转和平移。最后,通过定义弹性模量降低5%的1/4梁几何结构(绿色)包含了各向异性梁刚度(见图 14)。

|
| 图 11 3D实体有限元模型(完整减震环外壳) Fig.11 3D solid finite element model(complete shock absorbing ring shell) |

|
| 图 12 3D模型轴承支撑 Fig.12 Bearing support of the 3D model |

|
| 图 13 3D模型转速 Fig.13 RPM of the 3D model |

|
| 图 14 3D模型各向异性刚度 Fig.14 Anisotropy stiffness of the 3D model |
共进行了2个模型的模拟:第一个模型使用光滑减震环,第二个模型为不连续减震环(见图 15),尺寸为25.4 mm × 6.35 mm。模拟加载步骤与2D模型相同。

|
| 图 15 3D模型减震环 Fig.15 Shock absorbing ring of the 3D model |
光滑减震环的侧向加速度模拟结果见图 16,加速度峰值大约为15g。从功率谱可以看出,反向涡动频率为4.73 Hz。计算得到信号的均方根值为3.98g,大于解析模型的1.19g和2D模型的1.21g。另外,在55~65 Hz、100~120 Hz和140~170 Hz之间较高的频率下观察到了激发,这在之前的模型中并不存在。

|
| 图 16 3D有限元模型侧向加速度记录和相应功率谱(光滑减震环) Fig.16 The lateral acceleration record and corresponding power spectrum of the 3D finite element model (smooth shock absorbing ring) |
不连续减震环的侧向加速度模拟结果见图 17。由图 17可以看出,侧向加速度主要介于20g~25g之间,但是一些峰值高达80g。反向涡动频率为4.5 Hz,略低于运动学解,可能表明BHA没有停留在无滑移涡动模式下,因此导致涡动频率降低。另外,功率谱显示了比光滑井眼模拟更宽的频率范围,激发在15~30 Hz、40~ 60 Hz、80~ 20 Hz和140~180 Hz之间存在。计算得到均方根值为7.09g,比光滑减震环的模拟结果高约80%。

|
| 图 17 3D有限元模型侧向加速度记录和相应功率谱(不连续减震环) Fig.17 The lateral acceleration record and corresponding power spectrum of the 3D finite element model(discontinuous shock absorbing ring) |
图 18显示了3D模拟过程中BHA的运动轨迹,垂直线清晰表明了BHA和减震环的静态位移。初始BHA位置位于减震环表面之上,但是由于质量不平衡和刚度各向异性,旋转时,BHA径向偏移,最终与减震环壁接触,摩擦引起BHA进入反向涡动(见图 18a)。图 18b显示了BHA在不连续减震环中的运动,显然,BHA的反向涡动轨迹被不连续中断。另外,BHA撞击不连续和减震环壁,而不是保持无滑移涡动,有助于侧向加速度信号中更高的频率激发。3D实体模型的计算精度得到了提高,但是计算成本也相应增加,在分布式4核PC机上模拟需要大约48 h[24]。

|
| 图 18 3D有限元模型轨迹图 Fig.18 3D finite element model trajectory |
3 试验研究
为了验证解析模型和有限元模型,利用反向涡动试验机分别进行了光滑减震环和不连续减震环试验。BHA外径171.45 mm,减震环内径215.90 mm,焊接在减震环内壁上的金属条用于不连续性试验。试验过程中BHA转速设为60 r/min,一旦系统进入稳态反向涡动,就使用数据采集系统采集数据。
光滑减震环试验结果见图 19,侧向加速度范围为20g~30g。从功率谱可以看出,反向涡动频率为4.65 Hz,与所有模型预测结果一致,激发在频率25 Hz、60 Hz和介于90~110 Hz之间存在,相应的均方根值为3.01g。

|
| 图 19 光滑减震环试验结果 Fig.19 Smooth shock absorbing ring test results |
不连续减震环试验结果见图 20。由图 20可以看出,加速度峰值介于40g~50g之间,反向涡动频率为4.73 Hz,意外地接近于运动学解,这是因为不连续非但没有提高涡动频率,反而引起BHA滑移,从而降低了涡动频率。激发在15~25 Hz、40~60 Hz、80 ~110 Hz和140~160 Hz之间存在,计算得到均方根值为7.28g[24]。

|
| 图 20 不连续减震环试验结果 Fig.20 Test results of discontinuous shock absorbing ring |
4 结果对比
首先对比了光滑减震环的反向涡动试验与解析模型和有限元模型预测的振动响应。结果表明,解析模型和2D有限元模型预测的涡动加速度幅值分别为1.7g和1.8g,而3D有限元模型预测的幅值大约为15g,一些峰值高达20g,与试验观察到的20g的峰值一致。在所有模型中,反向涡动频率都得到了正确预测,模型和试验结果与4.70 Hz的运动学解一致,而且3D有限元模型中的一些较高频率与试验结果一致。但是,无论是解析模型,还是2D有限元模型,都没有预测较高的频率激发。在模拟中,55~65 Hz、90~110 Hz和140~160 Hz之间频率范围内,侧向加速度的功率谱与试验结果一致(见图 21)。此外,解析模型和2D有限元模型的均方根值大约为1.2g,然而3D有限元模型预测值与试验值更接近,3D有限元模型均方根值为3.98g,而试验值为3.01g。考虑到这些结果,在预测某些条件下反向涡动的起始和反向涡动频率时,解析模型和2D有限元模型十分有用。由于模型简化,这两个模型计算的加速度低于试验结果。另外,集中质量假设避免了较高的频率激发,因此均方根值也低于试验值。然而,3D有限元模型精确预测了响应幅度、反向涡动频率、较高的激发频率和均方根值,因此是预测精确的反向涡动响应的最佳工具。

|
| 图 21 3D模型和试验(光滑减震环)的频率对比 Fig.21 Frequency comparison of the 3D model and test (smooth shock absorbing ring) |
随后对比了不连续减震环的反向涡动试验与解析模型和有限元模型预测的振动响应。2D有限元模型和3D有限元模型预测的侧向加速度幅值在20g~30g之间变化,然而,3D有限元模型的一些峰值高达80g。虽然侧向加速度幅值略低于40g(一些峰值高达60g)的试验值,仍具有可比较性。2D有限元模型预测的反向涡动频率不准确,原因可能是减震环中切口的复杂接触特性及集中质量假设。从图 10和图 18可以明显看出,BHA运动没有呈现相同的涡动轨迹,导致计算的涡动频率存在差异。3D有限元模型预测的涡动频率接近试验结果。涡动频率预测值和测量值低于预期,3D有限元模型涡动频率预测值为4.50 Hz,试验测量值为4.73 Hz。可以预计涡动频率高于4.70 Hz的运动学解,这是因为不连续减少了减震环的有效内径。然而,较低的涡动频率值表明了源于与不连续接触的滑移结果,降低了涡动频率,模型接触结果验证了该特性。另外,功率谱观察表明,由于不连续的存在,导致较高的激发频率产生。3D有限元模型精确预测了15~25 Hz、40~65 Hz、80~110 Hz和140~180 Hz之间的激发频率,且在反向涡动试验中也进行了测量(见图 22)。相应地,3D有限元模型与试验得到的均方根值一致,均为7.28g。不连续减震环3D有限元模型通过试验结果得到了验证,并有效预测了高达200 Hz的激发频率[24]。

|
| 图 22 3D模型和试验(不连续减震环)的频率对比 Fig.22 Frequency comparison of the 3D model and test (discontinuous shock absorbing ring) |
5 结论
(1) 钻井振动威胁到BHA的寿命和可靠性,侧向振动是引起BHA故障的主要原因之一,严重情况下,BHA会出现反向涡动。
(2) 预测模型证实,光滑和不连续井眼条件下,BHA可能发生摩擦接触引起的反向涡动。采用反向涡动试验机对模型预测结果进行了验证,结果表明3D有限元模型计算的振动幅值与试验结果一致,2D有限元模型和3D有限元模型预测的反向涡动频率与试验结果和运动学解也一致。另外,3D有限元模型预测的较高的激发频率和均方根值也得到了验证。
(3) 用逼真的不连续井眼进行全尺寸BHA反向涡动试验,可以了解钻井过程中的非线性振动。实验室试验并结合数值模拟,为确定BHA反向涡动效应和特征提供了科学方法,有助于优化BHA设计,提高BHA可靠性,最终提高钻井性能。
| [1] |
SUGIURA J, SAMUEL R, OPPELT J, et al.Drilling modeling and simulation: current state and future goals[R].SPE 173045, 2015.
|
| [2] |
MACPHERSON J D, PAUL P, BEHOUNEK M, et al.A framework for transarency in drilling mechanics and dynamics measurements[R].SPE 174874, 2015.
|
| [3] |
BREHME J, TRAVIS T. Total BHA reliability-an improved method to measure success[R].SPE 112644, 2008.
|
| [4] |
FINNIE I, BAILEY J J. An experimental study on drill-string vibrations[J]. Journal of Engineering for Industry, 1960, 82(2): 129-135. DOI:10.1115/1.3663020 |
| [5] |
SPANOS P D, CHEVALLIER A M, POLITIS N P, et al. Oil and gas well drilling:a vibrations perspective[J]. Shock & Vibration Digest, 2003, 35(2): 85-103. |
| [6] |
PASLAY P R. Drill string vibrations due to intermittent contact of bit teeth[J]. Asme Journal of Engineering for Industry, 1963, 85(2): 187-195. DOI:10.1115/1.3667632 |
| [7] |
KYLLINGSTAD A, HALSEY G W. A study of slip/stick motion of the bit[R].SPE 16659, 1987.
|
| [8] |
MITCHELL R F, ALLEN M B. Lateral vibration:the key to BHA failure analysis[J]. World Oil, 1985, 200(4): 101-106. |
| [9] |
HEISIG G, NEUBERT M. Lateral drillstring vibrations in extended-reach wells[R].SPE 59235, 2000.
|
| [10] |
BESAISOW A A, PAYNE M L. A study of excitation mechanisms and resonances inducing bottomhole-assembly vibrations[R].SPE 15560, 1988.
|
| [11] |
BRETT J F, WARREN T M, BEHR S M. Bit whirl: a new theory of pdc bit failure[R].SPE 19571, 1989.
|
| [12] |
WARREN T M, OSTER J H. Torsional resonance of drill collars with PDC bits in hard rocks[R].SPE 49204, 1998.
|
| [13] |
LEDGERWOOD L W, HOFFMANN O J, JAIN J R, et al.Downhole measurement and modeling reveal stick-slip as a primary cause of PDC bit damage in today's applications[R].SPE 134488, 2010.
|
| [14] |
RECKMANN H, JOGI P, KPETEHOTO F T, et al. MWD failure rates due to drilling dynamics[R].SPE 127413, 2010.
|
| [15] |
SCHWEFE T, LEDGERWOOD L W, JAIN J R, et al. Development and testing of stick/slip-resistant PDC bits[R].SPE 168026, 2014.
|
| [16] |
OUESLATI H, HOHL A, MAKKAR N, et al. The need for high frequency vibration measurement along with dynamics modeling to understand the genesis of PDC bit damage[R].SPE 167993, 2014.
|
| [17] |
BOWLER A, HARMER R, LOGESPARAN L, et al. Continuous high-frequency measurement of the drilling process provide new insights into drilling-system response and transitions between vibration modes[R].SPE 170713, 2014.
|
| [18] |
OUESLATI H, JAIN J R, RECKMANN H, et al. New insights into drilling dynamics through high frequency vibration measurement and modeling[R].SPE 166212, 2013.
|
| [19] |
JAIN J R, OUESLATI H, HOHL A, et al. High-frequency torsional dynamics of drilling systems:an analysis of the bit-system interaction[J]. SPE 167968, 2014. |
| [20] |
HOHL A, TERGEIST M, OUESLATI H, et al. Derivation and experimental validation of an analytical criterion for the identification of self-excited modes in drilling systems[J]. Journal of Sound & Vibration, 2015, 342(8): 290-302. |
| [21] |
SHEN Y L, ZHANG Z X, ZHAO J, et al. The origin and mechanism of severe stick-slip[R].SPE 187457, 2017.
|
| [22] |
ZHANG Z, SHEN Y, CHEN W, et al. Continuous high frequency measurement improves understanding of high frequency torsional oscillation in North America land drilling[R].SPE 187173, 2017.
|
| [23] |
HOHL A, HERBIG C, AREVALO P, et al. Measurement of dynamics phenomena in downhole tools-requirements, theory, and interpretation[R].SPE 189710, 2018.
|
| [24] |
POPP T, STIBBE H, HEINISCH D, et al.Backward whirl testing and modeling with realistic borehole contacts for enhanced drilling tool reliability[R].SPE 189600, 2018.
|
| [25] |
JANSEN J D. Whirl and chaotic motion of stabilized drill collars[R].SPE 20930, 1992.
|


