0 引言
泥页岩地层钻井中的井壁失稳是全球油气开发面临的普遍问题,成为影响钻井速度及钻井成本的关键因素之一。渤海油田是我国海上最大的油田和重要的原油生产基地,浅层油气资源的开发已较为成熟,中深层油气资源的勘探开发将成为渤海油田未来增储上产的主要途径。渤海湾盆地东营和沙河街组地层硬脆性泥页岩广泛存在,该类地层裂隙发育、性脆,钻井过程中易发生井壁坍塌、掉块或掉片的现象,进而导致憋压,甚至造成阻卡及卡钻。实际上,由于硬脆性泥页岩渗透率低,与钻井流体相互作用下,井壁围岩在不同时刻不同深度表现出不同的孔压变化,这种变化作用在岩石骨架上会引起岩石的体积应变,与此同时,变形的骨架反过来也会作用于孔隙流体。
与常规的井壁稳定分析有较大不同,硬脆性泥页岩的井壁失稳问题是一个复杂的岩石力学及钻井液化学的流固耦合问题[1-2]。M.A.BIOT[3]通过引入Biot系数建立了考虑流固耦合作用下的多孔介质弹性理论。J.P.CARTER等[4]系统地建立了流固耦合多孔介质二维井周应力解。E.DETOURNAY等[5]以平面应变条件假设为基础,推导出Carter应力解的二维一般形式,通过Stehfest算法将空间域的井周应力解反演至时间域,研究孔隙压力和应力场的变化规律。L.CUI等[6-7]进一步将Detournay的二维形式推广至三维井周应力解。A.MEHRABIAN等[8]应用Fourier和Laplace变换直接推导出三维井周应力解形式。Y.ABOUSLEIMAN[9-11]和G.Z.CHEN等[12-13]相继给出了各向同性地层和横观各向同性地层中流固及流固热耦合条件下的井周应力与孔隙压力解析解。国内刘玉石、何湘清、王兴隆和蔚宝华等[14-17]运用热弹性理论研究了温度对井壁稳定的影响。
笔者根据渤海油田硬脆性泥页岩组构特征和理化性能对其变形破坏规律进行了研究,探讨了流固耦合对井周岩石的应力和变形场的影响规律。研究结果在一定程度上揭示了流固耦合对硬脆性泥页岩地层井壁失稳的影响机理。
1 硬脆性泥页岩微观结构分析利用CT扫描电镜观察渤中A井东三段泥页岩岩样微观结构,结果如图 1所示。

|
| 图 1 渤中A井东三段泥页岩CT扫描电镜图 Fig.1 CT scanning electron micrograph of the shale in the third member of Dongying formation in Well Bozhong A |
电镜扫描结果表明,硬脆性泥页岩孔缝发育,样品较为致密,渗透率较低,粒间存在孔缝,孔缝宽度为5~12 μm。层面状结构以及粒间孔缝均有利于钻井液渗流。水分子以渗流方式进入裂缝,会与围岩发生流固耦合作用进而影响井周应力分布。
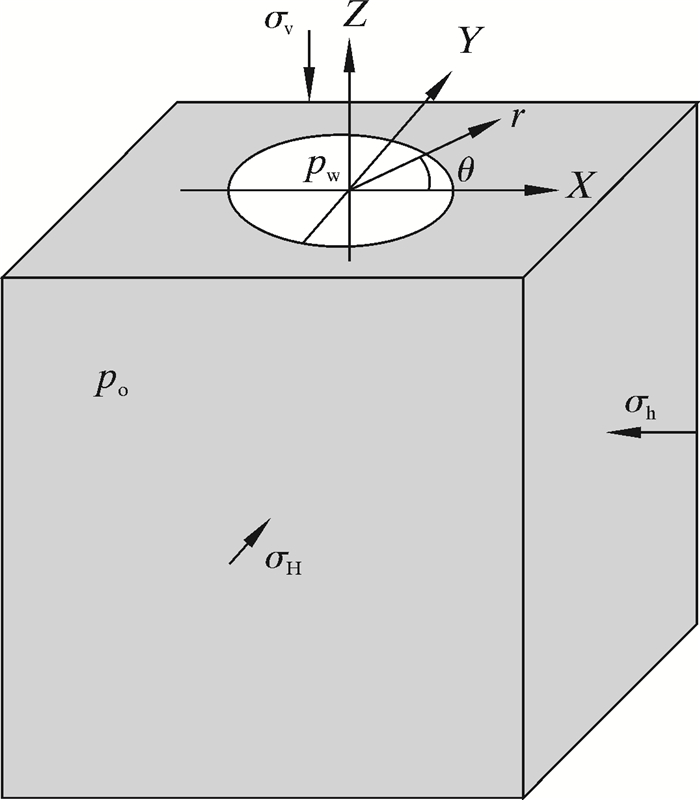
2 井壁稳定流固耦合计算模型假设钻井过程井孔形成的时间可以忽略(井壁孔隙压力处于原始状态),井轴与所建坐标系的Z轴平行,流固耦合井壁稳定分析井筒模型应力和压力分布如图 2所示。图 2中:在无穷远处的地应力分别为σH、σh和σv,井筒半径为a,液柱压力为pw,初始孔隙压力为po, 井壁处孔隙压力为pi。孔隙压力与泥饼性质有关。
|
| 图 2 井筒应力和压力分布图 Fig.2 Wellbore stress and pressure distribution |
对于直井,极坐标下考虑孔隙弹性的井周应力分布为[3]:
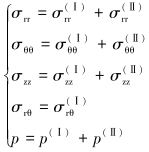
|
(1) |
式中:σrr、σθθ、σzz、σrθ、p分别表示径向应力、周向应力、轴向应力、r-θ平面剪应力以及孔隙压力。
该问题的求解可以通过线性叠加原理将其分解为两个次问题,符号“Ⅰ”和“Ⅱ”分别代表问题一和问题二[3]。
问题一是一个孔隙弹性狭义平面应变问题,孔隙压力和井周围岩应力分布包含了3种模型求解,解析解如式(2)所示。
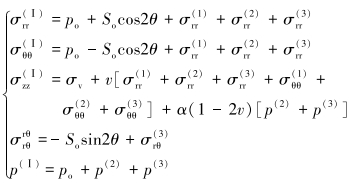
|
(2) |
其中:
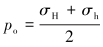
|
(3) |
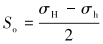
|
(4) |
式(2)中的1、2、3分别对应着下面的3种模型。3种模型中,无穷远处(r→∞)边界条件为:
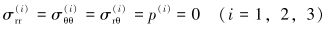
|
(5) |
模型1,r=a,边界条件为:
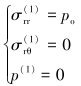
|
(6) |
模型2,r=a,边界条件为:
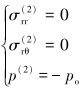
|
(7) |
模型3,r=a,边界条件为:
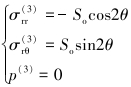
|
(8) |
模型1是轴对称问题,符号“~”代表对变量进行拉普拉斯转换处理(下同),结合边界得到井周应力及孔压分布:
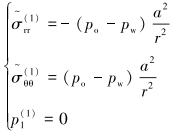
|
(9) |
模型2在拉普拉斯变换域的解析解为:
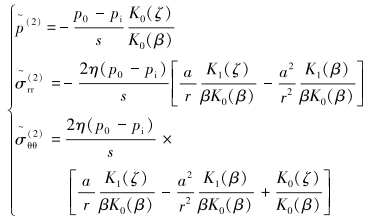
|
(10) |
式中:K0和K1分别代表零阶和一阶第二类贝塞尔函数。
其中:
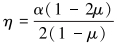
|
(11) |
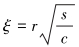
|
(12) |
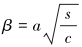
|
(13) |
式中:s是拉普拉斯转换参数,α是BIOT系数,μ是岩石排水泊松比,c是岩石固结系数。
模型3是非对称问题,必须先做出一定的变换才能得到,具体求解过程可参考文献[18],模型3在拉普拉斯变换域的解析解为:
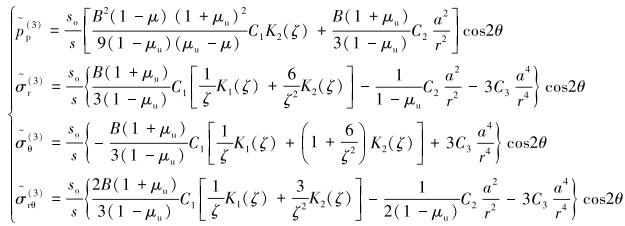
|
(14) |
其中:
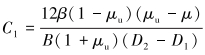
|
(15) |
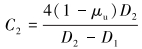
|
(16) |
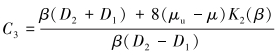
|
(17) |
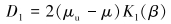
|
(18) |
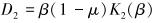
|
(19) |
式中:μu是岩石非排水泊松比,β是Skempton系数。
对于模型2和模型3,需要从拉普拉斯域s到时间域t变换,利用拉普拉斯数值反演Stehfest方法进行求解,式(20)和式(21)即为Stehfest算法的主体[19]。
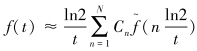
|
(20) |
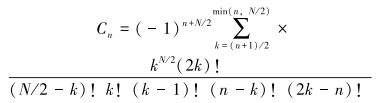
|
(21) |
由于舍入误差的影响,N一般取值为6~18。
问题二是一个弹性单轴压缩问题,单轴压缩问题为纯弹性力学问题,对场变量(与时间相关)无贡献,其表达式为:
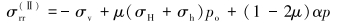
|
(22) |
最终,将孔隙弹性狭义平面应变问题和弹性单轴压缩问题进行叠加获得该问题的完整解。
3 算例分析利用上述解析方程,对渤海油田BZ34油田中深层直井A井(受正断层控制)进行了井壁稳定流固耦合分析,该井最小地应力方位为北偏东75°,计算中采用的参数如表 1所示。
| 垂深/m | 上覆岩层压力/MPa | 水平最大地应力/MPa | 水平最小地应力/MPa | 原始孔隙压力/MPa | 液柱压力/ MPa | 井壁处孔隙压力/MPa | 岩石渗透率/mD |
| 3 000 | 69 | 65 | 45 | 30 | 35 | 30~35 | 30 |
| 流体黏度/ (mPa·s) | 岩石剪切模量/GPa | 岩石黏聚力/MPa | 岩石内摩擦角/(°) | 岩石孔隙比 | 岩石泊松比 | 岩石非排水泊松比 | Skempton系数 |
| 50 | 7.5 | 14 | 25 | 0.05 | 0.20 | 0.467 | 0.935 |
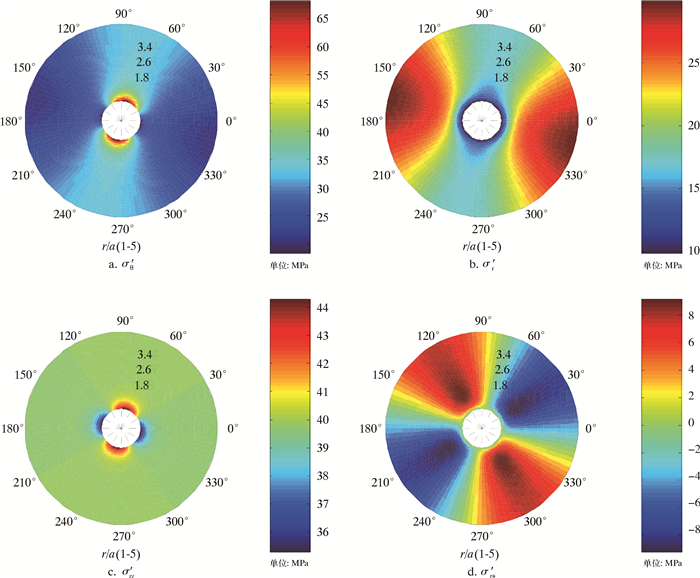
图 3为钻开井眼瞬间5倍井眼井周应力分布。
|
| 图 3 钻开井眼瞬间井周应力分布 Fig.3 Wellbore stress distribution at the moment of drilling out the wellbore |
根据计算结果可知,周向应力最大值、径向应力最小值和轴向应力最大值出现在水平最小地应力方位,井壁上剪应力为0。由于在最小地应力方位,周向应力与径向应力差值最大,井眼最易在最小地应力方位发生坍塌破坏。
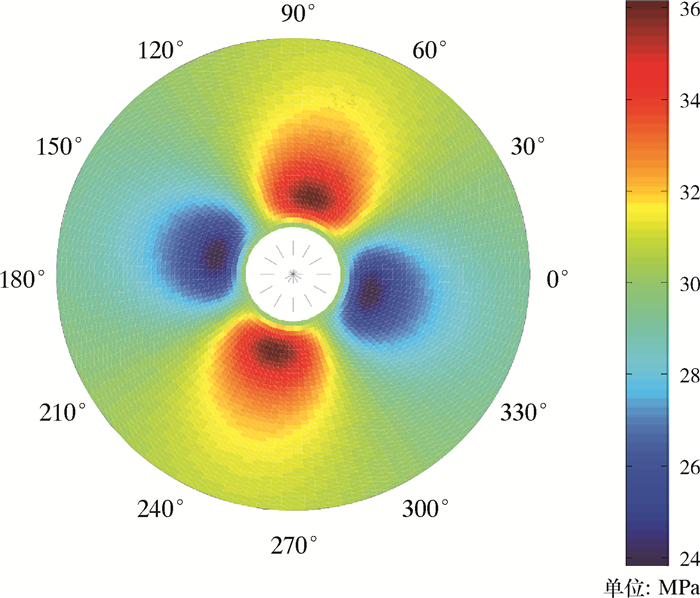
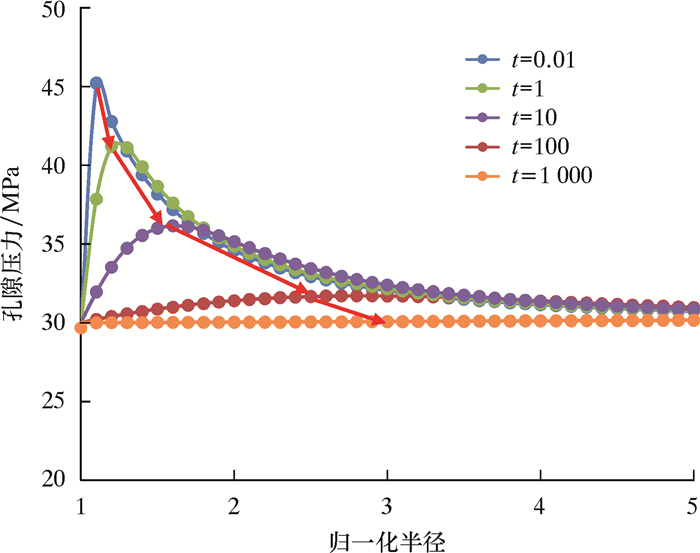
图 4为井眼钻开瞬间井周孔隙压力分布。结果显示,硬脆性泥页岩渗透率较低,井周孔隙压力在流固耦合作用下容易憋压,在井周方向表现出较强的非均匀特征。孔隙压力的最高值并非出现在井壁上,而是在水平最小地应力方位距离井壁非常近的位置处。由于受地层和液柱压力挤压效应,最大孔隙压力比液柱压力大,孔隙压力最小值出现在水平最大地应力方向距离井壁非常近的位置处。图 5为最小地应力方位不同时刻下孔隙压力随半径的变化关系。从计算结果可以看出,随着时间的延长,孔隙压力最大值向地层深处扩散,并逐渐趋于原始孔压。
|
| 图 4 钻开井眼瞬间井周孔隙压力分布 Fig.4 Pore pressure distribution at the moment of drilling out the wellbore |
|
| 图 5 钻开井眼后不同时刻下最小地应力方位孔隙压力分布 Fig.5 The pore pressure distribution at the moment of drilling out the wellbore in direction of the minimum horizontal in-situ stress at different time |
岩石坍塌破坏引入破坏比系数K,其值大于1表示井眼发生了坍塌破坏。破坏比系数计算公式为:
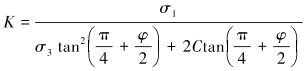
|
(23) |
式中:σ1为最大主应力,MPa;σ3为最小主应力,MPa;C为基体黏聚力,MPa;$φ$为基体内摩擦角,(°)。
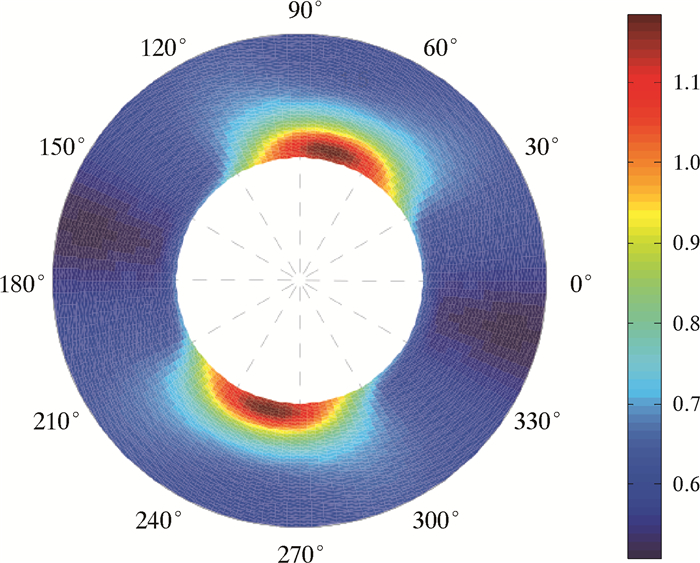
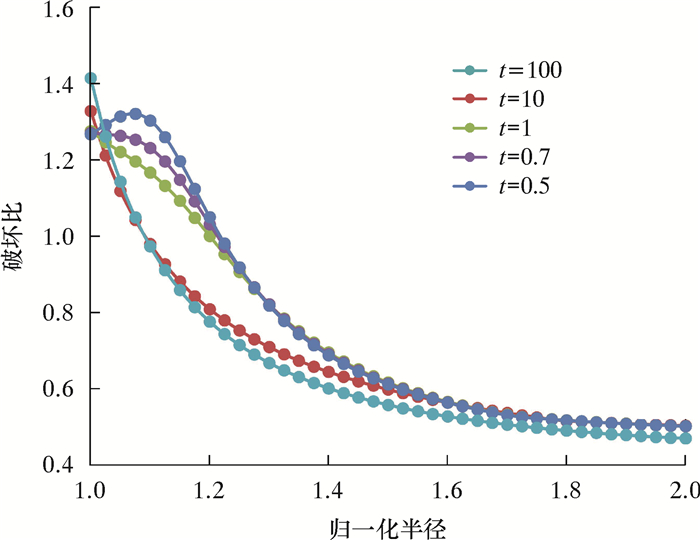
图 6为井眼钻开瞬间井周破坏情况。由图 6可看出,井眼破坏首先发生在水平最小地应力方位距离井壁非常近的位置处。图 7为最小地应力方位不同时刻下井周破坏情况。
|
| 图 6 钻开井眼瞬间井周破坏比分布 Fig.6 The failure ratio distribution of borehole at the moment of drilling out the wellbore |
|
| 图 7 不同时刻下最小地应力方位破坏比 Fig.7 The failure ratio of borehole in direction of the minimum horizontal in-situ stress at different time |
计算结果显示,随着钻开时间的延长,破坏区由井壁内部向井壁发展,而且呈现破坏程度先降低后增长的趋势。表现在工程中,对于某些特定情况下,硬脆性泥页岩地层在井壁内部首先破坏,如果岩石微裂隙逐渐扩展相互融合,则可能会引起较大掉块式的坍塌。
钻井液滤液等外来流体侵入会改变硬脆性泥页岩井周孔压。为研究钻井液封堵系数对井壁失稳的影响,引入破坏比系数λ,即封堵系数。封堵系数值为1表示完全不具备对裂纹的封堵能力,无法在裂纹与井筒间形成有效的封隔层,裂纹内的流体压力等于井筒压力;封堵系数值为0表示完全具备对裂纹的封堵,裂纹内流体压力等于原始孔压。λ的表达式为:
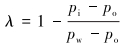
|
(24) |
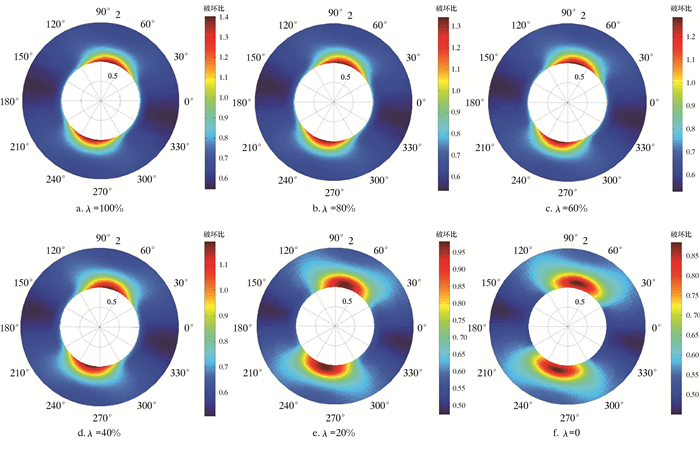
图 8表示在钻井液不同封堵系数条件下井周破坏情况。结果显示,随着钻井液封堵性的提高,地层破坏程度降低,当封堵系数为20%以下时,地层将不产生坍塌破坏。因此对于渗透率较低的硬脆性泥页岩地层,保持钻井液良好的封堵性有助于防止地层产生井壁破坏。
|
| 图 8 t=1 s时刻不同封堵系数条件下井周破坏比 Fig.8 The failure ratio of borehole under different plugging factors at t=1 s |
4 结论
(1) 井眼钻开后,由于钻井液与地层相互挤压并向地层滤失,流固耦合和滤失效应共同影响井周孔隙压力的变化,钻开瞬间最小地应力方位的地层孔隙压力迅速升高,孔隙压力最大值出现在水平最小地应力方位的井壁附近,随着钻开时间的延长,井周孔隙压力向地层深处扩散,并逐渐趋于原始孔压。
(2) 在最小地应力方位井壁内部某处最容易发生地层失稳,井周地层的最大破坏比随钻开时间的延长呈现破坏程度先降低后增长的趋势。
(3) 随着钻井液封堵性的提高,地层坍塌破坏程度降低,为避免井眼发生大面积坍塌,在工程上可以加强钻井液的封堵性,以控制液柱压力向井周的扩散。
| [1] |
曹文科, 邓金根, 蔚宝华, 等. 基于多孔介质热弹性理论的井壁诱导缝成因[J]. 天然气工业, 2017, 37(6): 79-85. CAO W K, DENG J G, YU B H, et al. Genesis of induced fractures on borehole walls based on the thermos-poroelasticity theory[J]. Natural Gas Industry, 2017, 37(6): 79-85. |
| [2] |
任保友, 蒲晓林, 曹成, 等. 纳米钻井液提高地层承压能力实验[J]. 石油钻采工艺, 2018, 40(2): 179-184. REN B Y, PU X L, CAO C, et al. Experimental study on improving the formation pressure-bearing capacity by using nano-drilling fluid[J]. Oil Drilling & Production Technology, 2018, 40(2): 179-184. |
| [3] |
BIOT M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155-164. DOI:10.1063/1.1712886 |
| [4] |
CARTER J P, BOOKER J R. Elastic consolidation around a deep circular tunnel[J]. International Journal of Solids and Structures, 1982, 18(12): 1059-1074. DOI:10.1016/0020-7683(82)90093-2 |
| [5] |
DETOURNAY E, CHENG A H D. Poroelastic response of a borehole in a non-hydrostatic stress field[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts. Pergamon, 1988, 25(3): 171-182. |
| [6] |
CUI L. Poroelasticity with application to rock mechanics[D]. Delaware: University of Delaware, 1995.
|
| [7] |
CUI L, CHENG A H D, ABOUSLEIMAN Y. Poroelastic solution for aninclined borehole[J]. Journal of Applied Mechanics, 1997, 64(1): 32-38. DOI:10.1115/1.2787291 |
| [8] |
MEHRABIAN A, ABOUSLEIMAN Y N. Generalized poroelastic wellbore problem[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(16): 2727-2754. |
| [9] |
ABOUSLEIMAN Y, ROEGIERS J C, CUI L, et al. Poroelastic solution of an inclined borehole in a transversely isotropic medium[C]//The 35th U.S. Symposium on Rock Mechanics(USRMS), June 5-7, 1995, Reno, Nevada, USA.
|
| [10] |
ABOUSLEIMAN Y, CUI L. Poroelastic solutions in transversely isotropic media for wellbore and cylinder[J]. International Journal of Solids and Structures, 1998, 35(34/35): 4905-4929. |
| [11] |
ABOUSLEIMAN Y, EKBOTE S. Solutions for the inclined borehole in a poro-thermo-elastic transversely isotropic medium[J]. Journal of Applied Mechanics, 2005, 72(1): 102-114. DOI:10.1115/1.1825433 |
| [12] |
CHEN G Z, EWY R T. Thermo-poro-elastic effect on wellbore stability[J]. SPE Journal, 2005, 10(2): 121-129. DOI:10.2118/89039-PA |
| [13] |
CHEN G Z, EWY R T. Thermo-poro-elastic effect on wellbore stresses in permeable rocks[C]//Gulf Rocks 2004, the 6th North America Rock Mechanics Symposium(NARMS), June 5-9, 2004, Houston, Texas, USA.
|
| [14] |
刘玉石, 周煜辉, 黄克累. 井眼温度变化对井壁稳定的影响[J]. 石油钻采工艺, 1996, 18(4): 1-4. LIU Y S, ZHOU Y H, HUANG K L. Temperature of borehole effect on well wall stability[J]. Oil Drilling & Production Technology, 1996, 18(4): 1-4. |
| [15] |
何湘清, 刘向君, 罗平亚. 温度扰动对井壁稳定和油田开发的影响[J]. 天然气工业, 2003, 23(1): 39-41. HE X Q, LIU X J, LUO P Y. Influence of temperature perturbation on borehole wall stabilization and oil field development[J]. Natural Gas Industry, 2003, 23(1): 39-41. DOI:10.3321/j.issn:1000-0976.2003.01.011 |
| [16] |
王兴隆, 程远方, 赵益忠. 钻井作业中泥页岩地层井壁稳定受温度影响的规律研究[J]. 石油钻探技术, 2007, 35(2): 42-45. WANG X L, CHENG Y F, ZHAO Y Z. The effect of temperature on wellbore stability in shales during drilling[J]. Petroleum Drilling Techniques, 2007, 35(2): 42-45. DOI:10.3969/j.issn.1001-0890.2007.02.013 |
| [17] |
蔚宝华, 卢晓峰, 王炳印, 等. 高温井地层温度变化对井壁稳定性影响规律研究[J]. 钻井液与完井液, 2004, 21(6): 17-20. YU B H, LU X F, WANG B Y, et al. Law of temperature influence on wellbore stability in hot well[J]. Drilling Fluid & Completion Fluid, 2004, 21(6): 17-20. |
| [18] |
金衍, 陈勉. 井壁稳定力学[M]. 北京: 科学出版社, 2012: 132-142. JIN Y, CHEN M. Borehole stability mechanics[M]. Beijing: Science Press, 2012: 132-142. |
| [19] |
同登科, 陈钦雷. 关于Laplace数值反演Stehfest方法的一点注记[J]. 石油学报, 2001, 22(6): 91-92. TONG D K, CHEN Q L. A note on Stehfest method of Laplace numerical inversion[J]. Acta Petrolei Sinica, 2001, 22(6): 91-92. DOI:10.3321/j.issn:0253-2697.2001.06.020 |


