2. 沈阳龙昌管道检测中心
2. Shenyang Longchang Pipeline Inspection Center
0 引言
随着我国油气管道总里程的不断增加,人们对管道运输安全问题的关注度也在增强。因此,定期对油气管道进行检测很有必要。漏磁检测操作简单,检测速度快,是油气管道检测的重要方式。对于不满足服役条件的管道,需要将其替换。但由于检测过程中管道被磁化至饱和状态或近饱和状态,导致检测后仍有一定的剩磁。在新旧管道对接过程中,由于管道剩磁的存在,焊接过程出现了电弧偏吹现象,这会影响焊接质量,不仅没有起到修补管道缺陷的作用,而且使得管道的质量下降。除此之外,管道中存在剩磁还有可能加剧管道内部腐蚀,与外部磁场相作用而加大管道缺陷等。
国内已经成熟的退磁方式均使用焊机电缆进行消磁,仅仅通过反向抵消焊口磁场,并没有解决管道带磁问题[1-2]。G.S SHELIKHOV等[3-4]设计了一种基于永磁铁的大口径管道退磁装置,但是一些相关技术并没有公布,仍需要攻克。笔者通过建立基于Maxwell的仿真模型与响应面分析模型,用该模型分析不同缺陷以及其他磁化参数对漏磁场强度的影响,然后进行试验,分析永磁铁退磁可行性,以期为管道退磁方法研究提供参考。
1 油气管道漏磁检测磁化特征分析铁磁材料磁化的原因很多,漏磁检测为主要的方法,因此笔者主要研究漏磁检测导致的磁化特征。20世纪60年代,苏联学者首先提出采用磁偶极子模型模拟工件表面缺陷及裂纹,开创了漏磁检测定量分析的先河。此后,这一领域逐渐发展成为两大学派。用磁偶极子法求解的经典理论学派和多用有限元求解的工程近似学派[5]。
工件表面缺陷模型共有3种:①点偶极子模型主要用来模拟点状孔、洞等缺陷;②线偶极子模型主要用来模拟低浅划道以及拉痕等缺陷;③面偶极子模型可以对裂纹和折迭等缺陷进行模拟。有限元分析方法将复杂问题分解成多个小部分问题或是分解成多个小的单元。求解域由许多有限元的域组成,对每一单元假定较简单的近似解,然后推导求解这个域总的满足条件,从而得到问题的解。大多数实际问题难以得到准确解,而采用有限元分析数值法不仅计算精度高,而且能适应各种复杂形状,是工程分析中比较有效的方法。
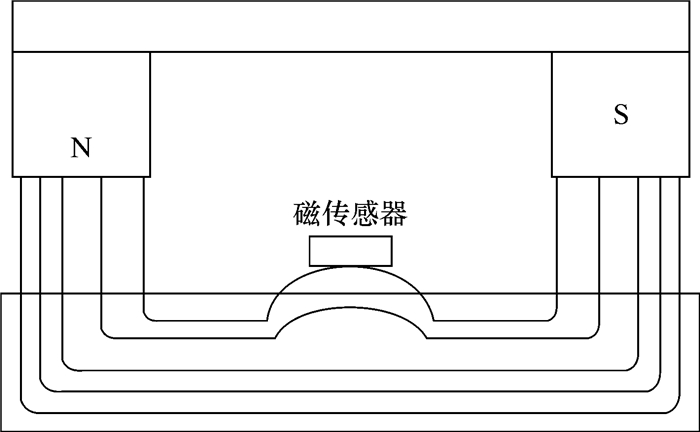
在外加磁场作用下,磁铁与管道之间的磁路闭合,磁力线会沿着管壁形成多个磁回路。如果两磁极之间存在缺陷,如裂纹、裂缝以及机械损伤等,磁力线将会在缺陷处泄漏。此时,在磁铁中间放置磁敏元件,就能有效识别并定位缺陷。在此之前,管道必须磁化至饱和或者近饱和状态,否则缺陷在其表面形成的漏磁场较小,很容易被噪声淹没。管道漏磁检测原理如图 1所示。
|
| 图 1 漏磁检测原理示意图 Fig.1 Schematic diagram of magnetic flux leakage detection |
在试验时,首先对管道施加外部激励,使得管道被充分磁化。若管壁没有缺陷产生,则磁力线与管的内表面基本上保持平行。管内存在缺陷时,由于空气的磁导率远远小于管道的磁导率,所以磁力线不再平行于管道内表面,内部的磁场会变形,从而发生“泄漏”。
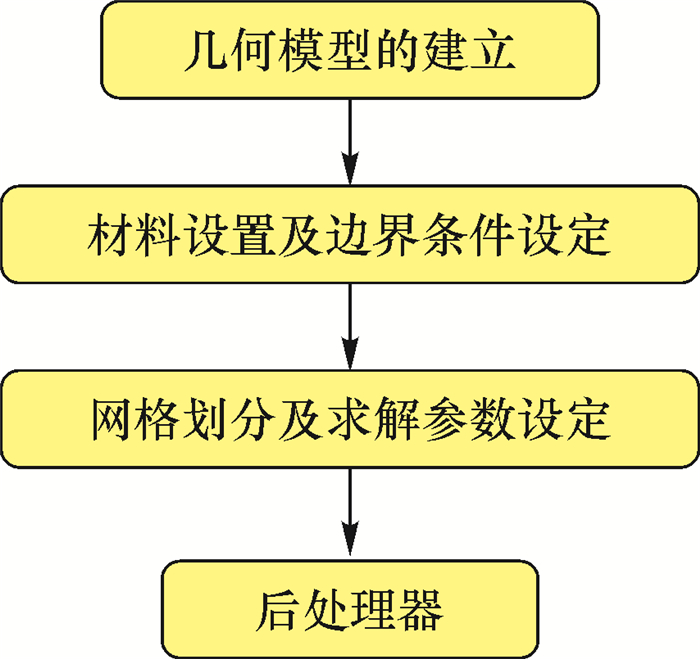
2 基于响应面法设计的磁化特征有限元模型 2.1 基于Maxwell磁化模型的建立Maxwell能够针对电磁场、静态磁场和动态磁场等进行模拟仿真。用户建模界面直观、简单,操作方便,数据处理功能强大,网格划分简单精确[6-9]。与其他有限元仿真软件相比,Maxwell主要有以下优点:①数据处理功能强大;②模型绘制方法简单方便;③可以对网格进行手动剖分,误差可控制;④求解器设置步骤简单。根据实际情况选择合适的计算模块,可以节省计算时间,提高效率。图 2所示为Maxwell有限元仿真操作流程图。
|
| 图 2 有限元仿真操作流程图 Fig.2 Finite element simulation operation flow chart |
2.1.1 几何模型建立
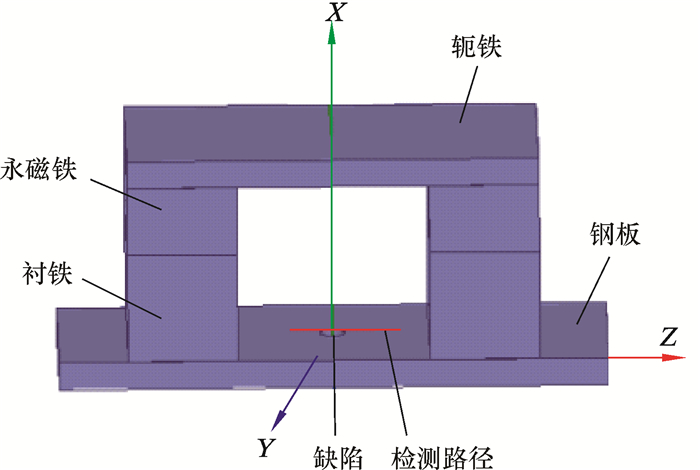
Maxwell模型绘制过程中可以使用各种各样的基本图形,设计者可以通过使用这些基本图形来绘制想得到的计算模型,建模过程方便快捷。使用Maxwell建立的永磁铁激励实体模型如图 3所示。该模型主要由永磁铁、衬铁、轭铁以及钢板等组成,模型各部分几何尺寸如表 1所示。缺陷为孔状缺陷,检测路径如图 3红线部分所示。
|
| 图 3 永磁铁激励实体模型 Fig.3 Permanent magnet excitation solid model |
| 名称 | 长 | 宽 | 高 |
| 钢板 | 120 | 60 | 7 |
| 永磁铁 | 40 | 20 | 10 |
| 衬铁 | 40 | 20 | 10/20/30 |
| 轭铁 | 100 | 40 | 10 |
2.1.2 材料设置及边界条件设定
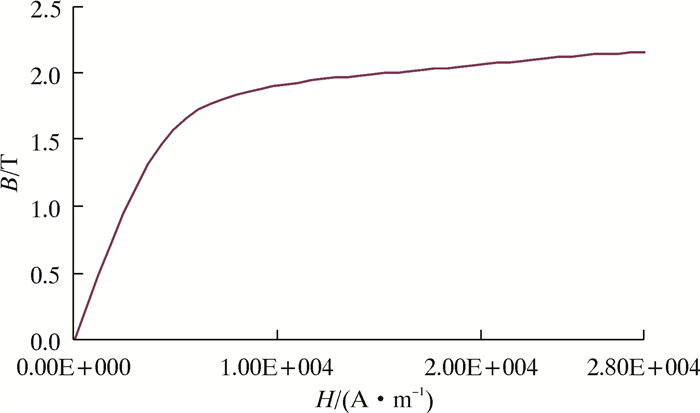
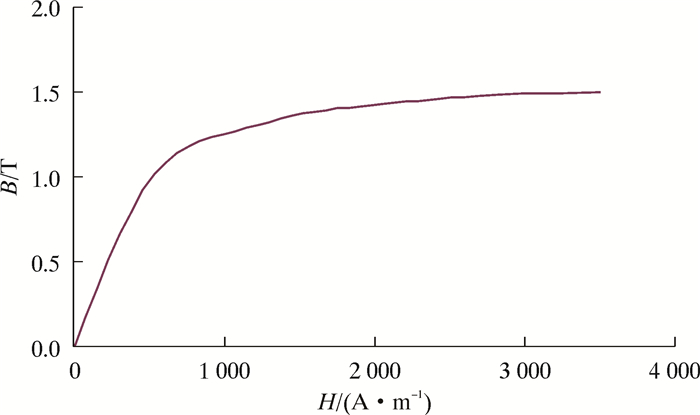
钢板采用X52钢,其BH曲线如图 4所示。图中B表示磁场强度,H表示磁导。衬铁、轭铁主要采用St37钢,其BH曲线如图 5所示。永磁铁磁导为-940 000 A/m,充磁方向为图 3中X方向,即垂直钢板方向[9]。
|
| 图 4 X52钢BH曲线 Fig.4 BH curve of X52 steel |
|
| 图 5 St37钢的BH曲线 Fig.5 BH curve of St37 steel |
有限元分析过程即为微分方程的求解过程。对于常微分方程来说,合理的边界条件是该方程存在唯一解的主要条件。Maxwell磁场求解过程包含自然边界条件、气球边界条件及主从边界条件等,设置边界条件为Insulating。
2.1.3 网格划分与求解参数设定网格划分影响到最后的计算时长和精度,因此合理的网格划分有助于提高计算效率。为提高计算精度,对于缺陷处的网格进行手动刨分,其余部分则选择自适应网格划分。
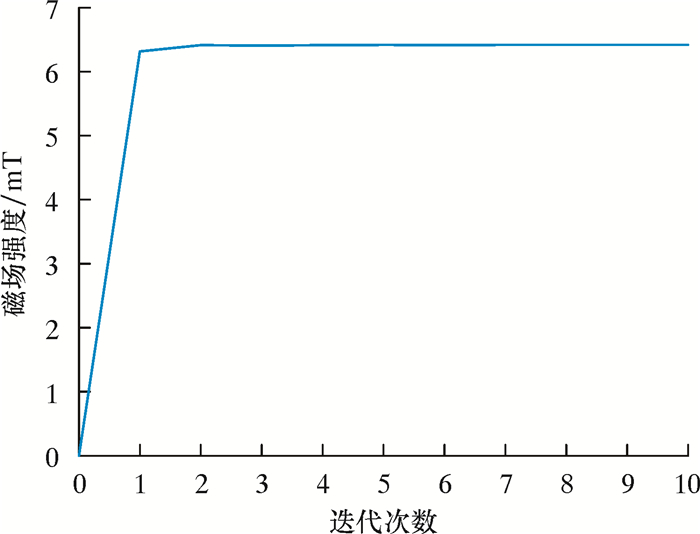
按照求解类型可分为静态求解器与瞬态求解器。静态求解器的迭加次数和计算精度可以手动进行设置,以保证仿真过程中结果的正确性,其网格数量与迭代次数以及初始刨分有关。图 6为迭代次数与缺陷中心磁场强度关系。从图 6可以看出,当迭代次数为4次以上时,误差可控制在0.01 mT。因此,在模拟过程中,设置迭代次数为10次,求解精度为0.1%。
|
| 图 6 迭代次数与缺陷中心磁场强度关系 Fig.6 Relationship between the number of iterations and the magnetic field strength of the defect center |
2.1.4 后处理分析
仿真结束后,可用Maxwell自带绘制曲线功能与场计算器显示求解结果,也可以导出数据,用其他软件进行图像绘制。
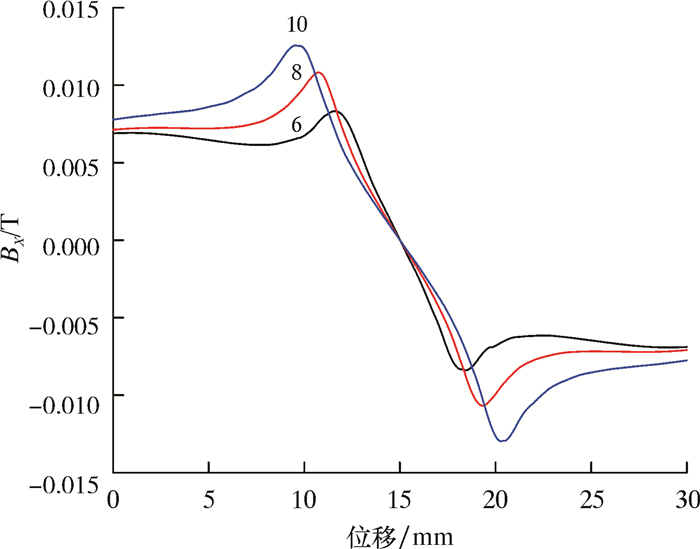
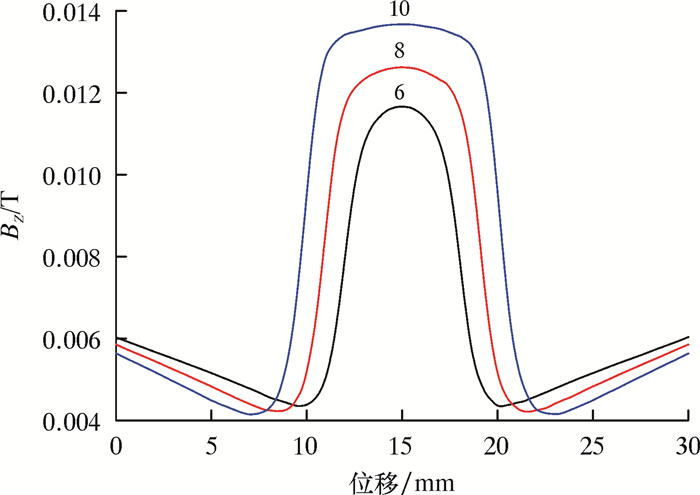
2.2 不同缺陷对磁化特征的影响钢板厚度为7 mm,在不同缺陷尺寸条件下对磁场强度影响进行仿真。当缺陷为通孔,缺陷半径为6、8及10 mm时,同一检测路径上磁场分布如图 7与图 8所示。从图 7和图 8可以看出,当深度一定时,缺陷半径越大,其X方向与Z方向磁通量密度也越大。
|
| 图 7 不同半径X方向磁通量密度 Fig.7 Magnetic flux density in X direction under different radius |
|
| 图 8 不同半径Z方向磁通量密度 Fig.8 Magnetic flux density in Z direction under different radius |
当缺陷为盲孔,缺陷尺寸为8 mm,深度分别为1、3、5和7 mm时,同一检测路径上磁场分布如图 9与图 10所示。
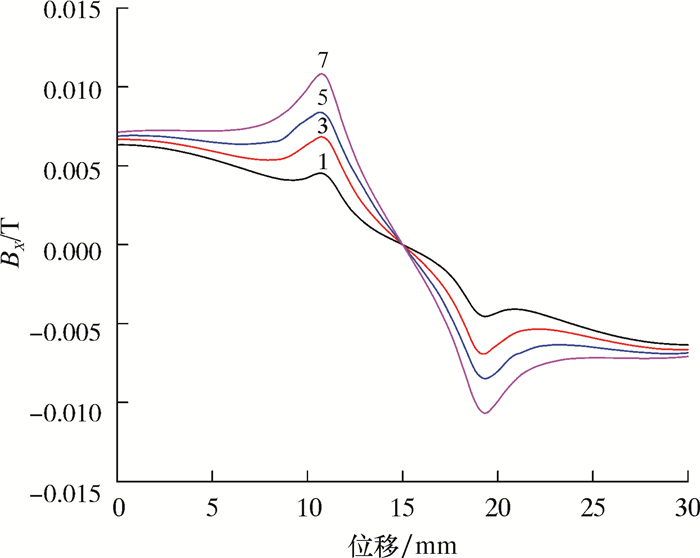
|
| 图 9 不同深度X方向磁通量密度 Fig.9 Magnetic flux density in X direction under different depths |
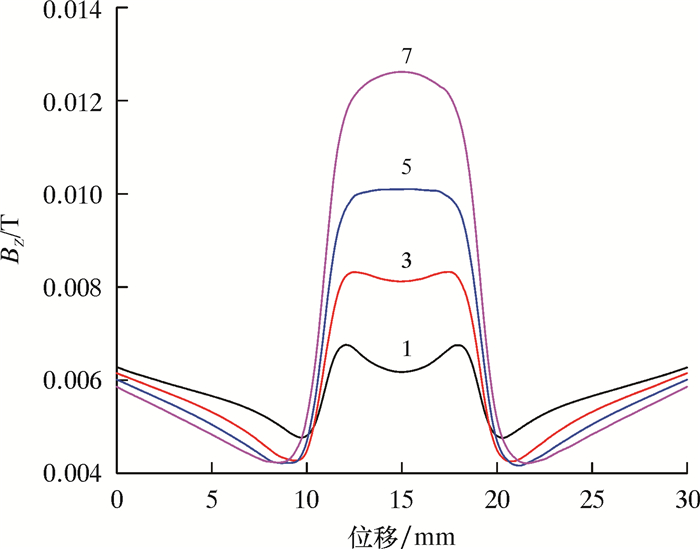
|
| 图 10 不同深度Z方向磁通量密度 Fig.10 Magnetic flux density in Z direction under different depths |
从图 9和图 10可以看出,当缺陷半径一定时,深度越大,其X方向与Z方向磁通量密度也越大。
2.3 磁化特征响应分析模型建立应用响应面法来研究不同缺陷尺寸对气隙处磁通量密度的影响。响应面法是一种数理统计方法,它通过分析样本点的个数与布局来判断不同影响因子对某一响应的影响程度。缺陷模型如图 11所示。当缺陷为孔状时,该模型主要有3个影响因子,分别为衬铁高度L、缺陷深度h以及缺陷半径r。分析因子及水平对照如表 2所示,结果借助Maxwell有限元电磁仿真软件代为计算[10-11]。
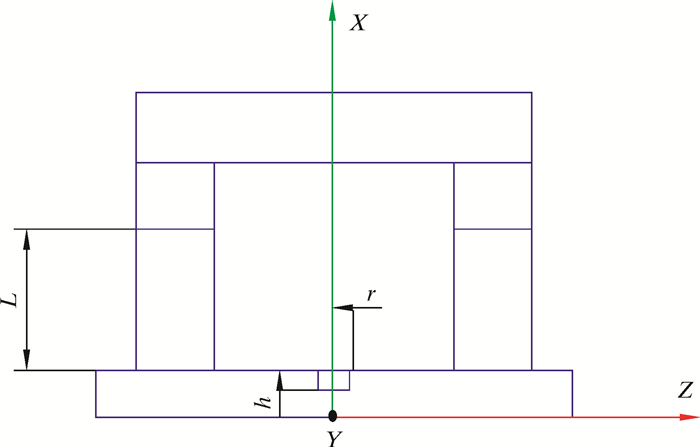
|
| 图 11 缺陷模型示意图 Fig.11 Schematic diagram of the defect model |
| 因子 | 水平 | ||
| -1 | 0 | 1 | |
| r | 6 | 8 | 10 |
| h | 1 | 4 | 7 |
| L | 10 | 20 | 30 |
根据BBD响应面法设计13组模拟试验,响应量B为缺陷中心点磁场强度。用有限元软件计算得到的响应量B如表 3所示。
| 序号 | r/mm | h/mm | L/mm | B/mT |
| 1 | 6 | 7 | 20 | 11.770 |
| 2 | 6 | 4 | 30 | 9.656 |
| 3 | 8 | 4 | 20 | 9.132 |
| 4 | 10 | 1 | 10 | 4.654 |
| 5 | 8 | 7 | 30 | 13.194 |
| 6 | 8 | 7 | 10 | 10.999 |
| 7 | 10 | 4 | 10 | 7.251 |
| 8 | 8 | 1 | 10 | 4.914 |
| 9 | 8 | 1 | 30 | 6.742 |
| 10 | 10 | 4 | 30 | 10.038 |
| 11 | 6 | 1 | 20 | 6.416 |
| 12 | 6 | 4 | 10 | 7.827 |
| 13 | 10 | 7 | 20 | 13.656 |
3个影响因子单独存在,它们相互作用及方差分析结果如表 4所示。
| 方差来源 | 平方和 | 自由度 | 均方 | F值 | P值 | 显著性 |
| r | 6.125E-04 | 1 | 6.125E-04 | 6.13E-03 | 0.939 1 | — |
| h | 90.400 | 1 | 90.400 | 905.06 | < 0.000 1 | ** |
| L | 9.330 | 1 | 9.330 | 93.40 | < 0.000 1 | ** |
| rh | 3.330 | 1 | 3.330 | 33.31 | 0.000 2 | * |
| rL | 0.230 | 1 | 0.2300 | 2.30 | 0.160 6 | — |
| hL | 0.034 | 1 | 0.034 | 0.34 | 0.574 4 | — |
| 模型 | 103.320 | 6 | 17.220 | 172.40 | < 0.000 1 | ** |
| 残差 | 1.000 | 10 | 0.100 | — | — | — |
| 失拟项 | 1.000 | 6 | 0.170 | — | — | — |
| 纯误差 | 0.000 | 4 | 0.000 | — | — | — |
| 总和 | 104.320 | 16 | — | — | — | — |
| 注:*表示显著(P < 0.05),**表示极显著(P < 0.000 1)。 | ||||||
通过对模拟试验结果进行响应面分析,经过二次拟合后,得到影响因子衬铁高度L、缺陷深度h及缺陷半径r与响应量磁场强度B之间的模拟方程如下:
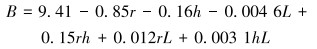
|
(1) |
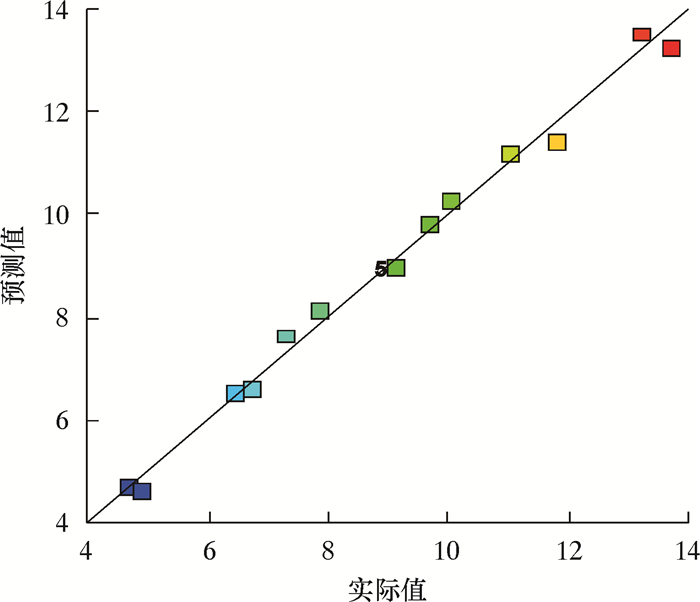
该回归模型F检验为极显著(P < 0.000 1),实际值与预测值误差如图 12所示。从图 12可见,该拟合方程与实际结果相符且误差较小。此时衬铁高度L、缺陷深度h及缺陷半径r与缺陷深度h的乘积rh是重要的影响因子。
|
| 图 12 实际值与预测值对比 Fig.12 Comparison of measured data and result of predictive model |
3 退磁样机结构设计与试验研究 3.1 退磁样机结构设计
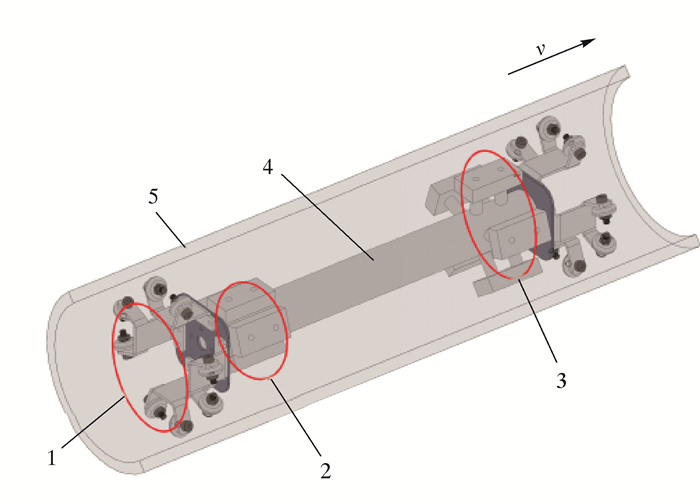
根据以上仿真结果设计的退磁样机整体结构如图 13所示。它主要由两环永磁铁、行走机构以及载体构成。轴承轮通过固定钣金以及支撑板固定。永磁铁、行走机构以及垫柱安装在载体上,垫柱厚度可调节,用来调整两环磁铁管壁的距离。行走机构除了可在管道内行走外,还可以保证运行磁铁与管道内壁的距离不会发生太大变化。
|
| 1—轮子;2—第一环永磁铁;3—第二环永磁铁;4—载体;5—管道。 图 13 退磁样机整体结构图 Fig.13 Overall structure of the demagnetization prototype |
3.2 试验原理及试验步骤
退磁试验系统包括交流退磁装置与永磁铁退磁试验装置。交流退磁试验装置主要包括直流充磁与交流退磁装置、双维度磁场测量台和高斯计等。
图 14为直流充磁与交流退磁装置。充磁过程中,将厚度为8 mm的钢板放入该装置中心位置,通过控制器控制输入线圈的电流,施加10、12及14 V电压,可实现不同强度的充磁。采用220 V、50 Hz交流电进行交流退磁。

|
| 图 14 直流充磁与交流退磁装置 Fig.14 DC magnetizing and AC demagnetization device |
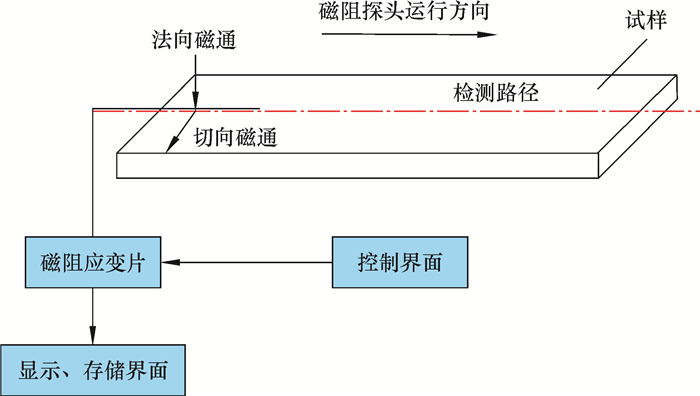
永磁铁简易退磁装置包括双维度磁场测量台、高斯计和永磁铁等。将两块永磁铁以一正一反固定,将厚度为8 mm的铁板在永磁铁不同磁场的位置划过。退磁后将钢板放入双维度磁场测量台中,测量台的探头接近钢板表面,通过控制界面调节在钢板表面移动的初始位置与运动速度,并保存在计算机中。磁场检测示意图如图 15所示。探头可以测量出钢板的切向磁通和法向磁通。
|
| 图 15 磁场检测示意图 Fig.15 Schematic diagram of magnetic field detection |
3.3 试验结果分析
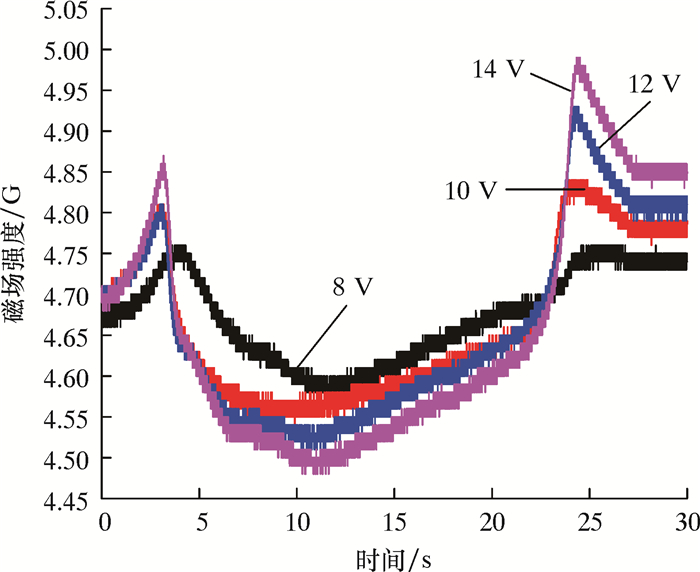
对8 mm厚的钢板施加不同电流强度进行充磁,径向和法向的磁通分别如图 16和图 17所示。
|
| 图 16 不同强度电流充磁钢板的切向磁通 Fig.16 Tangential magnetic flux of steel plate magnetized with different intensity currents |
|
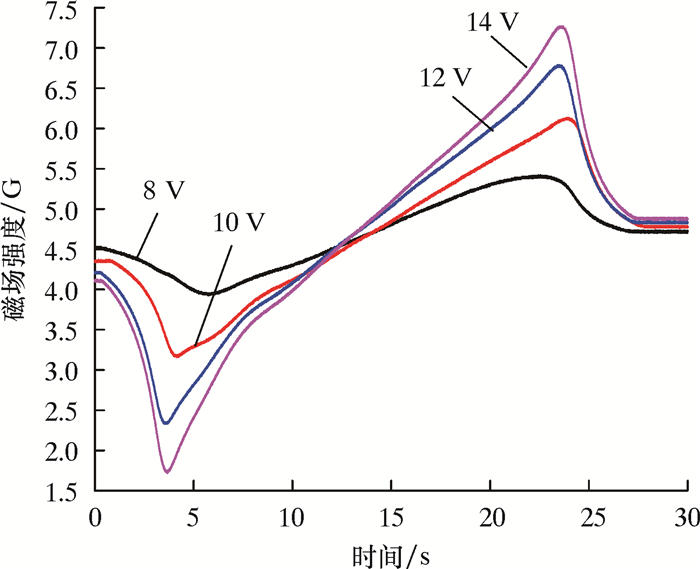
| 图 17 不同电流强度充磁钢板的法向磁通 Fig.17 Normal magnetic flux of steel plate magnetized with different intensity currents |
从图 16和图 17可以看出,随着外部磁场的不断增大,钢板两端切向磁通与法向磁通极性有增强的趋势。
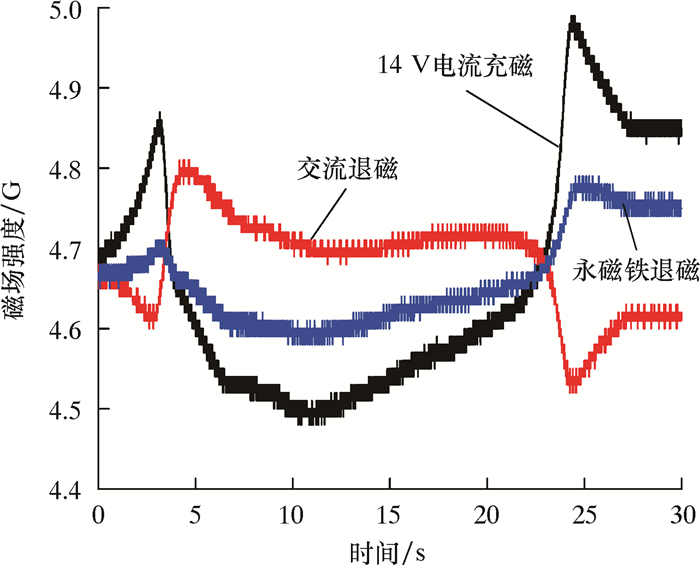
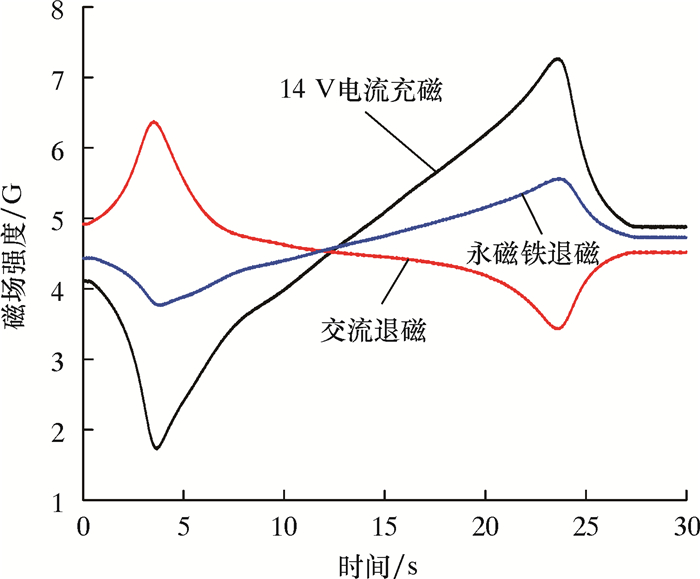
采用不同退磁方法退磁后,其径向和法向磁通如图 18和图 19所示。从图 18和图 19可以发现,永磁铁退磁对于钢板两端极性有一定的削弱作用,达到了较好的退磁效果。
|
| 图 18 不同方法退磁钢板的切向磁通 Fig.18 Tangential magnetic flux of steel plate during demagnetization by different methods |
|
| 图 19 不同方法退磁钢板的法向磁通 Fig.19 Normal magnetic flux of steel plate during demagnetization by different methods |
4 结论
(1) 基于Maxwell的磁化模型仿真结果表明:当缺陷深度一定时,半径越大,其X方向与Z方向磁通量密度也越大;当缺陷半径一定时,深度越大,其X方向与Z方向磁通量密度也越大。
(2) 建立基于缺陷的有限元仿真模型,通过响应面分析可以看出,衬铁高度L与缺陷深度h对于缺陷中心磁场强度影响显著。
(3) 退磁试验结果表明:随着外部磁场增大,钢板两端切向磁通与法向磁通极性有增强的趋势;永磁铁退磁对于钢板两端极性有一定的削弱作用,达到了较好的退磁效果。因此,简化后的退磁样机具有一定的可行性。
| [1] |
崔嘉, 黄文俊, 杨安益, 等. 长输天然气管道焊口带磁的产生原因及消磁方法[J]. 天然气工业, 2011, 31(7): 74-76. CUI J, HUANG W J, YANG A Y, et al. Typical transient working conditions of gas transmission pipelines[J]. Natural Gas Industry, 2011, 31(7): 74-76. DOI:10.3787/j.issn.1000-0976.2011.07.018 |
| [2] |
张科, 贾春龙, 张研, 等. 埋地输气管道消磁施焊方法讨论[J]. 石油工业技术监督, 2015, 31(5): 28-30. ZHANG K, JIA C L, ZHANG Y, et al. Discussion on degaussing welding method of buried gas pipeline[J]. Technology Supervision in Petroleum Industry, 2015, 31(5): 28-30. DOI:10.3969/j.issn.1004-1346.2015.05.009 |
| [3] |
SHELIKHOV G S, LOZOVSKY V N, KRASILNIKOV V A, et al.Device for demagnetization of main pipelines: RU2285254[P].2006.
|
| [4] |
SHELIKHOV G S. Pipe tools demagnetizing technique for main pipelines[J]. Materials Evaluation, 2014, 72(6): 646-651. |
| [5] |
黄松岭. 油气管道缺陷漏磁内检测理论与应用[M]. 北京: 机械工业出版社, 2013.
|
| [6] |
郑彪华, 何文, 周松强, 等. 管道缺陷漏磁检测的三维有限元仿真分析[J]. 中国安全科学学报, 2013, 23(12): 35. ZHENG B H, HE W, ZHOU S Q, et al. Research on numerical simulation of three-dimensionalmagnetic flux leakage inspection of pipeline defects[J]. China Safety Science Journal, 2013, 23(12): 35. DOI:10.3969/j.issn.1003-3033.2013.12.006 |
| [7] |
莫漫漫. 环状永磁体表面径向磁通密度分布的模拟计算[J]. 材料开发与应用, 2017, 32(3): 73-80. MO M M. Simulation calculation of radial magnetic flux density distribution on the surface of annular permanent magnets[J]. Development and Application of Materials, 2017, 32(3): 73-80. |
| [8] |
党娜, 王维斌, 张涛, 等. 管道腐蚀脉冲涡流检测的三维仿真与试验[J]. 无损检测, 2017, 39(2): 57-60. DANG N, WANG W B, ZHANG T, et al. 3D Simulation and experiment of pulsed eddy current testing for pipeline corrosion[J]. Nondestructive Testing, 2017, 39(2): 57-60. |
| [9] |
宣建青.高速钢轨漏磁无损检测的仿真与实现[D].南京: 南京航空航天大学, 2010. XUAN J Q.Simulation and implementation of non-destructive testing of high-speed rail leakage[D].Nanjing: Nanjing University of Aeronautics, 2010. |
| [10] |
崔婉婷.轴向励磁的管道漏磁内检测磁饱和问题研究[D].沈阳: 沈阳工业大学, 2015. CUI W T.Investigation of magnetic saturation in magnetic flux leakage of axial excited pipe[D].Shenyang: Shenyang University of Technology, 2015. |
| [11] |
张涛, 赵弘, 王维斌, 等. 基于响应面法的瞬变电磁法聚焦线圈优化设计[J]. 电子测量技术, 2016, 39(7): 28-32, 38. ZHANG T, ZHAO H, WANG W B, et al. Response surface methodology based transient electromagnetic method focusing coil optimum design[J]. Electronic Measurement Technology, 2016, 39(7): 28-32, 38. DOI:10.3969/j.issn.1002-7300.2016.07.006 |


