0 引言
由于我国陆地及近海油气资源的有限性,远离大陆架的深水油气开发现已成为我国未来能源战略的重点。在深水油气开发过程中,由于深水海况及海床土体参数与陆地及近海环境有着很大的不同,深水油气开发领域往往具有巨大的风险性。对于深水领域所采用的半潜式钻井平台来讲,井口系统已不能如浅水平台一般设置在平台之上,水下井口系统因而成为了深水钻采工艺中其稳定工作的重要保证。
水下井口系统主要由水下防喷器组(Subsea BOP)、水下井口头及导向架等子系统构成。其向上通过挠性接头连接隔水管系统,向下通过井口头套管挂连接导管及套管组系统。水下井口系统整体受隔水管拖曳力,自体受海流作用力、套管组悬挂力及导管作用于井口头的地基反力等诸多作用力。因此,分析在工作环境下的水下井口系统受力情况,对保证油气钻采工程的安全有效进行具有一定的参考意义。
分析水下井口系统中防喷器组子系统的受力特性时,需提前确定其所处环境下拖曳系数以获得其在海流作用下具体的受力参数。贾星兰等[1]利用标准几何体模型,通过量纲分析法研究了拖曳系数,确定了对一已有模型来讲,拖曳系数CD仅与雷诺数Re相关,并通过试验确定了两者的相互关系。苏堪华等[2-3]对隔水管拖曳系数取用1.0进行处理。林秀娟等[4]在分析水下采油树下放过程中,以拖曳系数非定值为前提,对系统力学特性进行了分析。S.E.ZEDLER等[5]考量了在不同海洋环境条件下的拖曳系数与理论确定值的偏差。在国内外分析隔水管和管桩等水下结构物的研究中,一般均采用圆柱体模型并通过雷诺数或经验来确定其拖曳系数[6-9]。综上所述,目前在研究海洋结构力学的相关文献中,确定拖曳系数的传统方法是将防喷器组假设为具有一定表面粗糙度的圆柱体,并通过计算流经其海水流体的雷诺数来确定[10]。
目前在海洋工程领域,一般在研究平台管桩时,对长径比较大的隔水管系统采用长圆柱体模型偏差亦不明显,但在水下井口力学特性分析中,对于表面结构十分复杂的BOP组、井口头及导向架组成的体系依旧采用圆柱体模型时,则将会与实际情况产生较大的偏差。笔者通过对井口系统在不同深度环境下的具体型号进行建模,并利用ANSYS中流固耦合模块对井口系统拖曳系数进行了仿真分析,同时考虑了海水水体在水体表面至工作深度范围中的各向异性,最终对不同深度下的井口系统拖曳系数进行了统计分析。研究结果可为水下井口力学分析提供一定的参考依据。
1 拖曳系数的经验确定方法在计算海洋环境载荷时,需要确定拖曳系数及惯性系数的大小。两个系数会直接关系到流体环境对作用力的大小。文献[1]利用量纲分析法,给出了单一结构体的拖曳系数仅与其所处流体环境下的流体雷诺数相关的证明。在海洋结构力学中,拖曳系数CD一般通过雷诺数Re加以确定。
通过雷诺数来确定拖曳系数的对应关系如表 1所示。具体操作时,还需考虑桩体上不规则粗糙面上相对表面粗糙度对拖曳系数的影响。一般相对表面粗糙度使拖曳系数增加100%时,其使桩体直径大约增加20%。
| 区间 | 雷诺数Re | 拖曳系数CD |
| 亚临界区 | Re < 2×105 | ≈1.2 |
| 临界区 | 2×105 < Re < 5×105 | ≈0.3 |
| 超临界区 | 5×105 < Re < 5×106 | 0.6~0.7 |
| 极临界区 | Re>5×106 | 0.6~0.7 |
在现今的水下井口力学研究领域中,均将水下井口系统(即包含BOP组、井口头及导向架等结构的系统)简化为圆柱体模型,在分析海水流体环境对其的影响时,亦采用设置圆柱体直径及通过雷诺数来判定其拖曳系数的方法[3, 11-12]。同时,在分析海水流体环境对水下系统的影响时,也大多将水体视作各向同性的水体,对于水黏度变化对水下井口系统受载情况的影响少有分析。
2 拖曳系数的确定 2.1 海水流体环境的确定在传统的水下井口力学分析中,拖曳系数CD通过雷诺数Re来确定。对于水下结构,其仅受海流力作用。海流力在流经结构物时,其雷诺数Re计算式为:
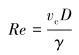
|
(1) |
式中:vc为该深度下最大可能海流流速,D为圆柱体结构物直径,γ为海水水体运动黏度。
vc依据美国船舶管理局经验公式确定[10]:
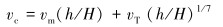
|
(2) |
式中:vm为水面风力海流速度,vT为水面表面潮流速度,h为计算深度距海底的高度(即井口系统高度),H为水深[13]。
在式(1)中,海水水体运动黏度γ受水温影响会发生明显变化。笔者采用我国南海海水水体作为算例的基本数据,即海水水体表层温度及海水水温阶跃层深度已知[14-15]。具体计算数据如表 2所示。
| 计算参数 | 数值 |
| 水体深度计算范围/m | 250~3 500 |
| 水体密度/(kg·m-3) | 1 030 |
| 表层水体温度/℃ | 20 |
| 水体温度阶跃层深度/m | 1 000 |
| 水面潮流速度/(m·s-1) | 1.0 |
| 风力海流速度/(m·s-1) | 1.0 |
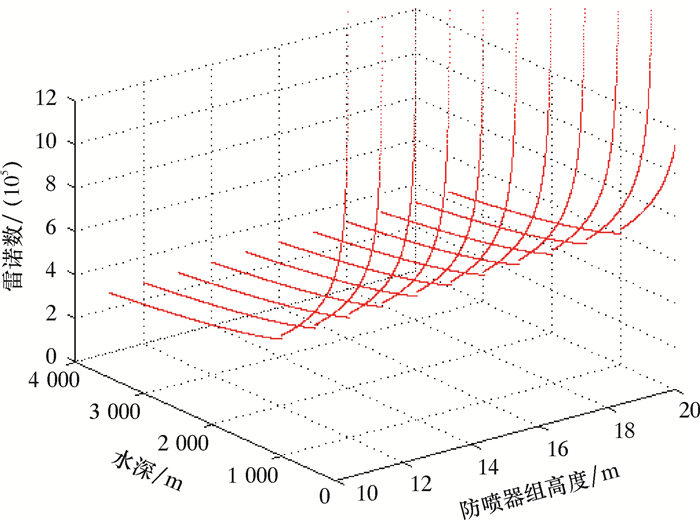
依据已知的海水温度与动力黏度的关系及海水水体密度,并忽略海水水体密度随水温的变化(变化较小,可以忽略),可算得流经不同型号(BOP组高度变化)的水下井口系统雷诺数,结果如图 1所示。
|
| 图 1 水下井口系统雷诺数分布示意图 Fig.1 Reynolds number distribution of subsea wellhead system |
由图 1可知,随着水深变化,水下井口系统雷诺数迅速下降,并在水温阶跃层以下趋于稳定。在深水环境下,据表 1可知,水体主要处于超临界区间,其拖曳系数CD应当在0.6~0.7之间选取。
2.2 拖曳系数的理论分析分析水下结构物受海流载荷时,采用Morison方程来确定所受的海流力,如式(3)所示:
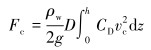
|
(3) |
式中:ρw为海水密度,g为重力加速度,Fc为海流力大小。
通过式(3)即可获得拖曳系数CD的值。
3 水下井口系统选型及建模采用Hydril公司的防喷器组单元的尺寸数据并以Transocean公司的深水防喷器选型经验作为依据,用于模拟分析的数据及模型如下所示[16-17]。
(1) 1 000 m级井口及BOP组系统:34.47 MPa(5 000 psi)挠性接头×1,34.47 MPa(5 000 psi)环形BOP×1,68.95 MPa(10 000 psi)双闸板BOP×2, 68.95 MPa(10 000 psi)级水下井口(见图 2a);

|
| 图 2 水下井口及BOP系统模型图 Fig.2 Model of subsea wellhead and BOP system |
(2) 2 000 m级井口及BOP组系统:34.47 MPa(5 000 psi)挠性接头×1,68.95 MPa(10 000 psi)环形BOP×1,68.95 MPa(10 000 psi)双闸板BOP×2, 68.95 MPa(10 000 psi)级水下井口(见图 2b);
(3) 2 500 m级井口及BOP组系统:68.95 MPa(10 000 psi)挠性接头×1,103.42 MPa(15 000 psi)环形BOP×1,103.42 MPa(15 000 psi)双闸板BOP×2, 103.42 MPa(15 000 psi)剪切或变径芯子单闸板BOP×2,103.42 MPa(15 000 psi)级水下井口(见图 2c);
(4) 3 000 m及以上级井口及BOP组系统:68.95 MPa(10 000 psi)挠性接头×1,103.42 MPa(15 000 psi)环形BOP×1,103.42 MPa(15 000 psi)双闸板BOP×2, 103.42 MPa(15 000 psi)剪切或变径芯子单闸板BOP×2,103.42 MPa(15 000 psi)级抗疲劳水下井口(见图 2d)。
4 考量水体分层特性的流固耦合模拟分析依据南海海水水体平均水温及温跃层数据,各型号BOP组及水下井口在水深250~3 500 m范围进行基于ANSYS流固耦合的模拟仿真计算,各层水体厚度为250 m,每层水体参数如表 3所示。
| 水深/m | 水温/℃ | 运动黏度/(m2·s-1) | 动力黏度/(kg·s·m-1) |
| 250 | 16.25 | 11.206 6×10-6 | 0.001 09 |
| 500 | 12.50 | 12.283 4×10-6 | 0.001 19 |
| 750 | 8.75 | 13.593 6×10-6 | 0.001 32 |
| 1 000 | 5.00 | 15.200 5×10-6 | 0.001 48 |
| 1 250 | 4.50 | 15.442 6×10-6 | 0.001 50 |
| 1 500 | 4.00 | 15.687 2×10-6 | 0.001 52 |
| 1 750 | 3.50 | 15.940 5×10-6 | 0.001 55 |
| 2 000 | 3.00 | 16.200 7×10-6 | 0.001 57 |
| 2 250 | 2.50 | 16.467 9×10-6 | 0.001 60 |
| 2 500 | 2.00 | 16.742 2×10-6 | 0.001 63 |
| 2 750 | 1.50 | 17.023 8×10-6 | 0.001 65 |
| 3 000 | 1.00 | 17.312 9×10-6 | 0.001 68 |
| 3 250 | 1.00 | 17.312 9×10-6 | 0.001 68 |
| 3 500 | 1.00 | 17.312 9×10-6 | 0.001 68 |
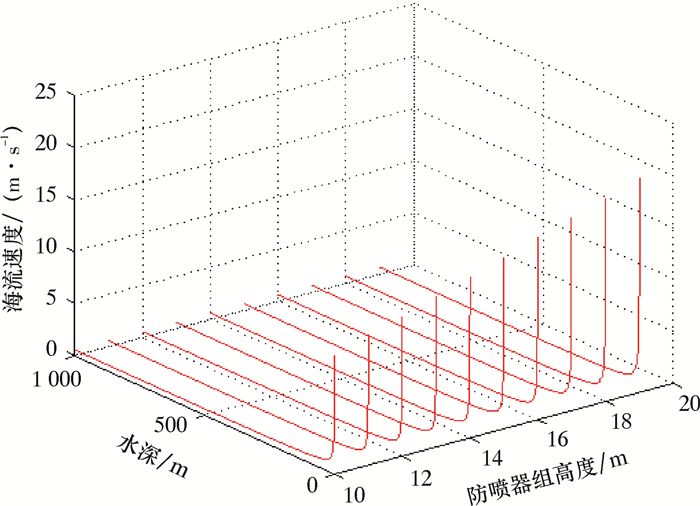
由表 3可知,不同层水体间参数变化较为明显,过往研究中将海水水体视为定值的计算分析存在较大偏差。依据式(2),对于不同高度的水下井口系统,流经其海水流速分布如图 3所示。
|
| 图 3 水体海流速度分布示意图 Fig.3 Current velocity distribution of seawater |
由图 3可知,随着海水深度增加,海流速度迅速趋于稳定。因此,式(3)中vc可视作在该井口系统高度h范围内为定值,拖曳系数CD可表示为:

|
(4) |
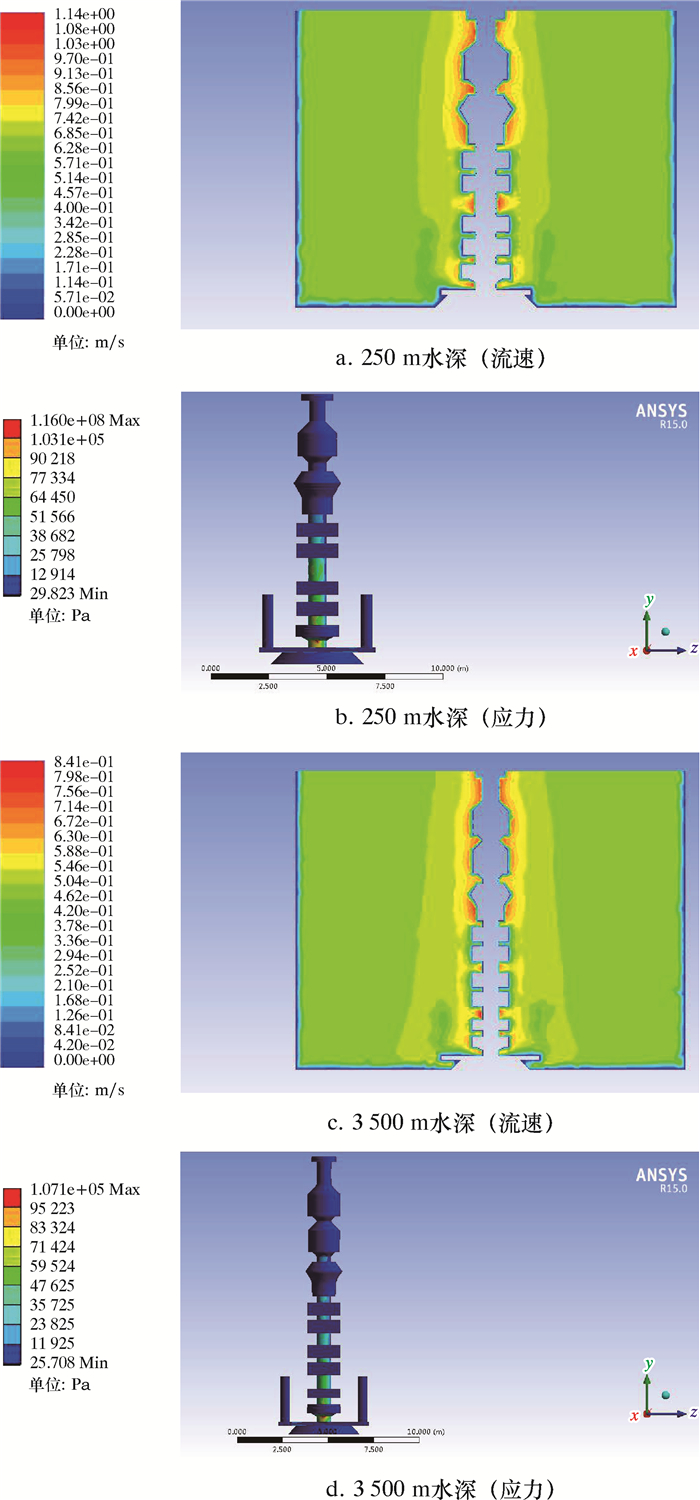
将表 3和图 3中流体密度、流速及黏度数据作为ANSYS流固耦合中流体参数,并针对不同层水体及不同型号的井口系统模型进行仿真计算,结果如图 4所示。
|
| 图 4 水下井口应力和流速分布 Fig.4 Stress distribution and current velocity of subsea wellhead |
5 计算结果分析
由于作用于水下井口模型的海流作用力是分布力,所以在计算分析时,将分布力等价于作用于模型上的集中力,并据式(4)进行计算。计算结果如表 4所示。
| 水深/m | BOP组/m | 拖曳系数 | |||||
| 级 | D | h | 计算值 | 平均值 | 方差/(10-6) | ||
| 250 | 1 000 | 1.531 | 11.625 | 0.862 | 0.863 | 1.250 0 | |
| 500 | 1 000 | 1.531 | 11.625 | 0.861 | 0.863 | 1.250 0 | |
| 750 | 1 000 | 1.531 | 11.625 | 0.864 | 0.863 | 1.250 0 | |
| 1 000 | 1 000 | 1.531 | 11.625 | 0.863 | 0.863 | 1.250 0 | |
| 1 250 | 2 000 | 1.536 | 11.695 | 1.040 | 1.079 | 0.003 7 | |
| 1 500 | 2 000 | 1.536 | 11.695 | 1.184 | 1.079 | 0.003 7 | |
| 1 750 | 2 000 | 1.536 | 11.695 | 1.046 | 1.079 | 0.003 7 | |
| 2 000 | 2 000 | 1.536 | 11.695 | 1.046 | 1.079 | 0.003 7 | |
| 2 250 | 2 500 | 1.616 | 14.080 | 0.607 | 0.607 | 0.000 0 | |
| 2 500 | 2 500 | 1.616 | 14.080 | 0.607 | 0.607 | 0.000 0 | |
| 2 750 | 2 500 | 1.616 | 14.080 | 0.607 | 0.607 | 0.000 0 | |
| 3 000 | 3 000 | 1.612 | 15.275 | 0.824 | 0.824 | 0.000 0 | |
| 3 250 | 3 000 | 1.612 | 15.275 | 0.824 | 0.824 | 0.000 0 | |
| 3 500 | 3 000 | 1.612 | 15.275 | 0.824 | 0.824 | 0.000 0 | |
由表 4可知,对应于不同水体的拖曳系数在一种井口系统型号下具有较高的一致性。虽然对于井口系统来讲,其所受的海流速度及水体黏度均不相同,但从结果分析,两者变化的共同效应令拖曳系数保持了较高的稳定性。不同型号BOP拖曳系数变化趋势如图 5和图 6所示。

|
| 图 5 不同型号BOP拖曳系数变化趋势 Fig.5 Trends of drag coefficients of different types of BOP |
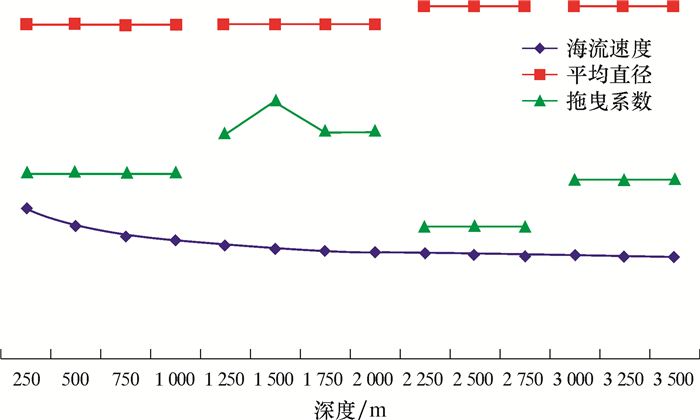
|
| 图 6 随深度变化的BOP参数变化趋势 Fig.6 Effect of depth on BOP parameters |
在流固耦合的模拟计算结果中,同一型号的井口系统拖曳系数大部分在小数点后三位保持一致。由此可见,尽管随着水深增加海流流速产生变化,但水下井口拖曳系数可以视为不变量。
6 结论综上所述,防喷器组拖曳系数模拟计算值较通过雷诺数判别的拖曳系数相对较大,且受防喷器组诸单元组成影响较大。当环形防喷器与闸板防喷器数量比例较大时,拖曳系数会明显减小。据以上研究结果,可以得出如下结论:
(1) 利用流固耦合及根据具体尺寸数据建模等方法完成了水下井口系统拖曳系数的计算,为分析井口力学特性提供了依据。
(2) 过往采用圆柱体用以假设BOP组及水下井口头组成的水下井口系统时存在较大误差,适用于不同水深的防喷器组的拖曳系数与自身结构相关关系大于其流经流体的雷诺数。
(3) 当环形防喷器单元数量与闸板防喷器单元数量比例较大时,井口系统拖曳系数会有减小的趋势。
(4) 即使海流速度随水深发生变化,但井口拖曳系数可视为一定值。
| [1] |
贾星兰, 方华灿. 海洋石油结构物阻力系数CD的实验研究[J]. 石油矿场机械, 1995, 24(4): 30-33. JIA X L, FANG H C. A experimental study on the resistance coefficient CD of marine petroleum structure[J]. Oil Field Equipment, 1995, 24(4): 30-33. |
| [2] |
LOPEZ C F, PORDAL H, BHALLA K, et al. Estimation of BOP stack drag and added mass using computational fluid dynamics[R]. OTC 27528-MS, 2017.
|
| [3] |
苏堪华.深水钻井井口力学分析及导管承载能力研究[D].东营: 中国石油大学(华东), 2009. SU K H. The research on subsea wellhead and casing bearing force in deep water[D]. Dongying: China University of Petroleum(Huadong), 2009. http://cdmd.cnki.com.cn/Article/CDMD-10425-2009221621.htm |
| [4] |
林秀娟, 肖文生, 王鸿雁. 深水采油树下放过程钻柱力学分析[J]. 中国石油大学学报(自然科学版), 2011, 35(5): 125-129. LIN X J, XIAO W S, WANG H Y. Drilling string mechanical analysis of running deep water oil tree[J]. Journal of China University of Petroleum (Edition of Natural Science), 2011, 35(5): 125-129. DOI:10.3969/j.issn.1673-5005.2011.05.023 |
| [5] |
ZEDLER S E, KANSCHAT G, HOTEIT I, et al. Estimation of the drag coefficient from the upper ocean response to a hurricane:a variational data assimilation approach[J]. Ocean Modelling, 2013, 68(49): 57-71. |
| [6] |
赵鹏良, 王嘉松, 蒋世全, 等. 海洋立管涡激振动的流固耦合模拟计算[J]. 海洋技术, 2010, 29(3): 73-77. ZHAO P L, WANG J S, JIANG S Q, et al. The fluid-structure simulation of vortex-induced vibration of marine riser[J]. Journal of Marine Technology, 2010, 29(3): 73-77. DOI:10.3969/j.issn.1003-2029.2010.03.017 |
| [7] |
陈禹.海洋深水管桩模型的涡激振动数值模拟研究[D].舟山: 浙江海洋大学, 2015. CHEN Y. The study of numerical simulation on the vortex-induced vibration of deep water pipe model[D]. Zhoushan: Zhejiang Ocean University, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y3029791 |
| [8] |
YANG W Y, AI Z J, ZHANG X D, et al. Nonlinear three-dimensional dynamics of a marine viscoelastic riser subjected to uniform flow[J]. Ocean Engineering, 2018, 149: 38-52. DOI:10.1016/j.oceaneng.2017.12.004 |
| [9] |
陈文礼, 周性坤, 郑苗子, 等. 基于微分变换法的海洋立管模态参数影响分析[J]. 石油机械, 2018, 46(1): 33-39. CHEN W L, ZHOU X K, ZHENG M Z, et al. Impact analysis of modal parameters of marine riser based on differential transformation method[J]. China Petroleum Machinery, 2018, 46(1): 33-39. |
| [10] |
杨进. ANSYS在海洋石油工程中的应用[M]. 北京: 石油工业出版社, 2010. YANG J. The application of ANSYS in offshore engineering of petroleum[M]. Beijing: Petroleum Industry Press, 2010. |
| [11] |
苏堪华, 管志川, 魏路, 等. 深水水上防喷器钻井系统水下井口稳定性分析[J]. 中国海上油气, 2009, 21(3): 180-185. SU K H, GUAN Z C, WEI L, et al. Stability analysis of subsea wellhead of surface blowout preventer system in deep water[J]. China Offshore Oil and Gas, 2009, 21(3): 180-185. DOI:10.3969/j.issn.1673-1506.2009.03.009 |
| [12] |
胡育佳.桩基非线性静动力学特性研究[D].上海: 上海大学, 2008. HU Y J. The research on non-linear static and dynamic characteristics of piles[D]. Shanghai: Shanghai University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-11903-2008198468.htm |
| [13] |
方华灿. 海洋石油工程[M]. 北京: 石油工业出版社, 2010. FANG H C. Offshore engineering of petroleum and gas[M]. Beijing: Petroleum Industry Press, 2010. |
| [14] |
沈建华, 周甦芳, 董玉来, 等. 2004年东海及黄海部分海域表层水温分布状况[J]. 海洋学研究, 2007, 25(3): 14-22. SHEN J H, ZHOU S F, DONG Y L, et al. The surface temperature distribution of east china sea and yellow sea in 2004[J]. Journal of Marine Science, 2007, 25(3): 14-22. DOI:10.3969/j.issn.1001-909X.2007.03.002 |
| [15] |
于非, 张志欣, 兰健, 等. 南黄海春季水温分布特征的分析[J]. 海洋科学进展, 2005, 23(3): 281-288. YU F, ZHANG Z X, LAN J, et al. The analysis of characters of temperature distribution of Yellow Sea and South China Sea in spring[J]. Advances in Marine Science, 2005, 23(3): 281-288. DOI:10.3969/j.issn.1671-6647.2005.03.005 |
| [16] |
NAKAGAWA E Y, MARTINS LAGE A C V. Kill and blow-out control development for deep water operations[R]. SPE 27497, 1994.
|
| [17] |
ROBERT D G. Blowout and well control handbook[M]. Beijing: Petroleum Industry Press, 2006.
|


