2. 中国石油大学(华东)山东省油气储运安全重点实验室;
3. 福建省水利水电勘测设计研究院
2. Shandong Province Key Laboratory of Oil and Gas Storage and Transportation Safety, China University of Petroleum (East China);
3. Fujian Provincial Investigation, Design & Research Institute of Water Conservancy & Hydropower
0 引言
脐带缆为多层非粘结螺旋缠绕结构,在外载的作用下,其内部构件间存在挤压接触及滑动摩擦等现象。国内外学者基于螺旋缠绕圆柱结构对其力学性能行为进行了大量机理性探究。现有解析方法基于小变形、线弹性材料以及忽略摩擦等假设,计算速度虽快,但准确性还需验证。脐带缆构造复杂且涉及挤压接触、滑动摩擦和大变形等问题,基于有限元理论的数值模拟方法在脐带缆结构分析中优势十分明显。
R.H.KNAPP等[1-3]对脐带缆截面受力变形进行了分析,并开发出可分析脐带缆整体变形和各构件应力响应的二维数值分析软件Cable CAD。M.A.J.DIXON等[4]利用有限元研究了脐带缆的疲劳寿命。V.LECORRE等[5]基于该模型,用梁单元替代壳单元对钢管进行模拟,在保证精度的前提下缩短了计算时间。H.MERINO等[6]基于ANSYS对脐带缆扭转荷载进行了建模研究。S.SæVIK等[7]对不同截面布局的脐带缆进行了模拟分析,并得出了脐带缆的拉伸刚度以及不同方向上的扭转刚度。杨志勋[8]分析了脐带缆截面布局对性能的影响。卢青针等[9]基于ANSYS中的梁单元与线线接触建立脐带缆有限元模型,分析了钢管脐带缆的弯曲刚度,在模型验证时只考虑了脐带缆的全滑动状态,且误差相对较大。肖能等[10]利用同样的方法对脐带缆的拉伸行为进行了有限元分析,但未考虑缠绕钢丝直径和外压等因素对拉伸行为的影响。近期,李伟民等[11]运用ANSYS从径向应力角度对脐带缆的截面布局进行了数值模拟研究。由于脐带缆有限元模型中存在大量接触单元,在保证计算精度的前提下,简化模型并提高计算效率,是现阶段脐带缆数值模拟分析的主要热点。
结合以上分析,笔者采用ANSYS建立了脐带缆的三维有限元模型,并考虑单元间的接触和摩擦,层间和层内的单元分别设置线面接触和线线接触,采用库仑摩擦模拟摩擦行为,既保证求解精度,也可提升计算效率。基于此,笔者对脐带缆的拉伸和弯曲力学性能进行模拟分析,且结果与相应的解析解相近,验证了有限元模型及模拟方法的可靠性,进而分析了不同参数对脐带缆截面力学性能的影响,以期为脐带缆的结构强度设计及优化分析提供参考。
1 脐带缆的结构特征及静强度解析模型 1.1 结构特征在不考虑脐带缆的外部保护套时,脐带缆结构主要由2部分构成:以填充物和电缆单元为主的中心圆柱直构件;以铠装钢丝为主的螺旋结构。脐带缆结构特征如图 1所示,螺旋结构缠绕在中心圆柱外部,可保证脐带缆拥有较高的拉伸刚度及较小的弯曲刚度。此外,脐带缆为多层结构,各层之间通过非粘接方式接触。在运行过程中,铠装钢丝可能发生滑动,进而导致脐带缆的力学性能发生变化。

|
| 1—填充物;2—钢管单元;3—电缆单元;4—内护套;5—铠装钢丝;6—外护套。 图 1 脐带缆的结构特征 Fig.1 Structural features of the umbilical cable |
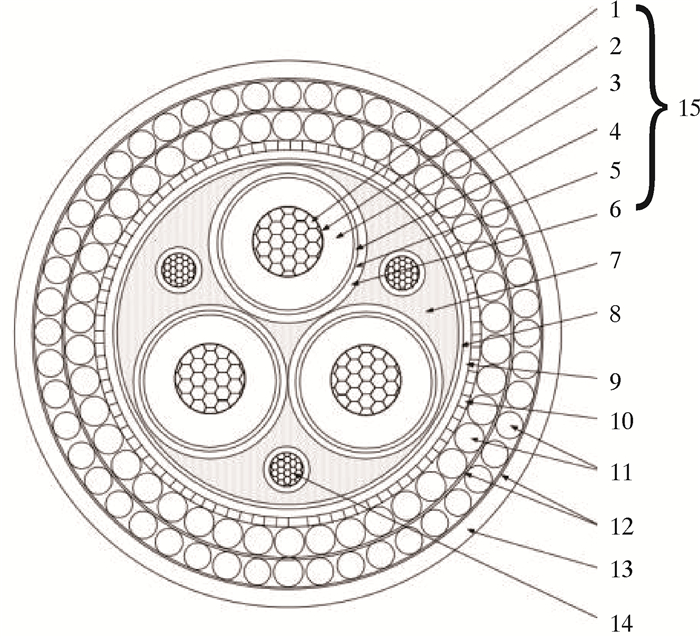
笔者以图 2所示的脐带缆为例进行研究,相应的规格如表 1所示。脐带缆主要由钢、铜和聚合物3种材料组成,相应的材料属性如表 2所示。
|
| 1—阻水导体;2—导体屏蔽;3—绝缘层;4—绝缘屏蔽;5—金属屏蔽;6—护套;7—填充物;8—绑扎带;9、13—护套;10—衬层;11—铠装钢丝;12—缓冲层;14—光纤;15—电缆。 图 2 脐带缆截面图 Fig.2 Cross-section of the umbilical cable |
| 序号 | 名称 | 厚度 | 外径 |
| 1 | 阻水导体 | 58 | 16.2 |
| 2 | 导体屏蔽 | 0.8 | 17.8 |
| 3 | 绝缘层 | 6.6 | 31.0 |
| 4 | 绝缘屏蔽 | 1.0 | — |
| 5 | 金属屏蔽 | 1×0.13 | — |
| 6 | 护套 | 1.5 | 36.4 |
| 7 | 填充物 | — | — |
| 8 | 绑扎带 | 2×0.3 | — |
| 9 | 护套 | 3.2 | 86.6 |
| 10 | 衬层 | — | — |
| 11 | 铠装钢丝 | ø5.0/55+62—16° | 111.7 |
| 12 | 缓冲层 | — | — |
| 13 | 护套 | 5.0 | 123.2 |
| 14 | 光纤 | — | 9.3 |
| 15 | 电缆 | — | 36.4 |
| 材料 | 弹性模量/GPa | 泊松比 | 密度/(kg·m-3) |
| 钢 | 206.0 | 0.30 | 7 800 |
| 铜 | 108.0 | 0.33 | 8 900 |
| 聚合物 | 1.5 | 0.48 | 1 000 |
1.2 静强度解析模型
在脐带缆设计阶段,拉伸刚度是考量其力学性能的关键参数之一,Knapp模型针对中心圆柱的径向收缩,提出中心圆柱为刚性材料(不发生径向收缩)或不可压缩材料(发生径向收缩, 但总体积不变)的假设[12]。Knapp模型的拉伸刚度解析公式为:
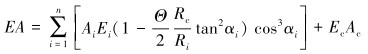
|
(1) |
式中:EA、EcAc分别为脐带缆整体和中心圆柱的拉伸刚度,其余部分为铠装钢丝拉伸刚度,Θ为不可压缩系数(Θ为0表示刚性材料;Θ为1代表不可压缩材料),n是铠装钢丝个数,Ai、Ei、αi分别为第i个铠装钢丝的横截面积、弹性模量和缠绕角度,Rc为中心圆柱的半径,Ri为第i个铠装钢丝截面中心到中心圆柱圆心的距离。
该模型下的脐带缆拉伸刚度为2个极限状态,其真实的拉伸刚度应介于二者之间。
脐带缆的弯曲性能呈现出比较强烈的非线性特征,产生这种特征的最主要原因就是脐带缆多层结构之间存在的接触和摩擦。J.A.WITZ等[13]解析模型忽略摩擦影响,并将脐带缆弯曲行为分为无滑动状态和全滑动状态。曲率较小时,铠装钢丝无法克服静摩擦及挤压约束,此时脐带缆处于无滑动状态;当曲率增加到一定程度,铠装钢丝全部发生滑动,此阶段脐带缆处于全滑动状态。无滑动到全滑动的过程复杂且短暂,一般不考虑。无滑动状态和全滑动状态下脐带缆的弯曲刚度计算公式如下。
无滑动状态:
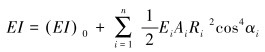
|
(2) |
全滑动状态:
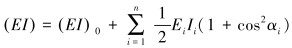
|
(3) |
式中:(EI)0为直构件的弯曲刚度,EiAi、EiIi分别为第i个铠装钢丝的拉伸刚度和弯曲刚度。
2 脐带缆有限元模型的建立与验证 2.1 有限元模型的建立在脐带缆的安装及在位作业工况,除铠装钢丝外,其他构件对其力学性能影响较小,可适当简化。其中,电缆功能单元缠绕角度较小,可简化为圆柱构件。所有材料均简化为各向同性材料,同时假设各功能单元间无空隙。
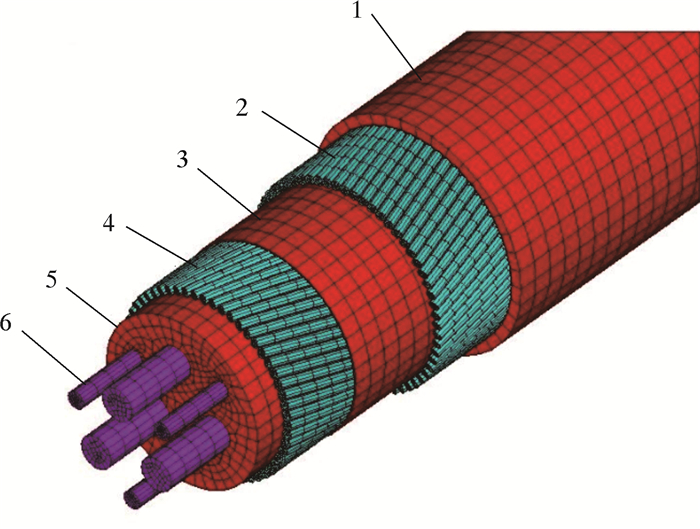
依据上述假设建立总长1 000 mm的有限元模型,铠装钢丝采用beam188模拟,其余部分均采用solid185模拟。网格划分后得到其有限元模型,如图 3所示。
|
| 1—外护套;2—外层钢丝;3—缓冲层;4—内层钢丝;5—填充物;6—功能单元。 图 3 脐带缆有限元模型 Fig.3 Finite element model of the umbilical cable |
模型由内至外一共5对接触对,采用conta177单元和targe170单元模拟铠装钢丝与其他构件之间的接触;采用conta176单元和targe170单元来模拟层内钢丝之间的接触。各接触对通过赋予库仑摩擦属性模拟构件间的摩擦行为。
模拟时,对脐带缆一端施加全约束,另一端面所有节点刚性连接到中心节点上。基于此,在中心节点上施加轴向拉伸或弯曲荷载,对模型进行静强度分析,并提取拉伸刚度及弯曲刚度等截面力学性能,同解析解对比以验证模型的可靠性。
2.2 基于拉伸刚度的模型验证在有限元模型一端施加全约束,另一端施加0.1 mm的轴向位移载荷。不考虑脐带缆内部摩擦,对模型进行加载求解。
提取模型的支反力为49 649 N,结合公式:
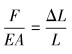
|
(4) |
式中:F为构件所受轴向拉力,ΔL为构件轴向变形量,L为构件长度。
将提取结果代入式(4),得到脐带缆整体拉伸刚度EA为:
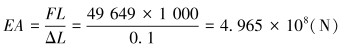
|
(5) |
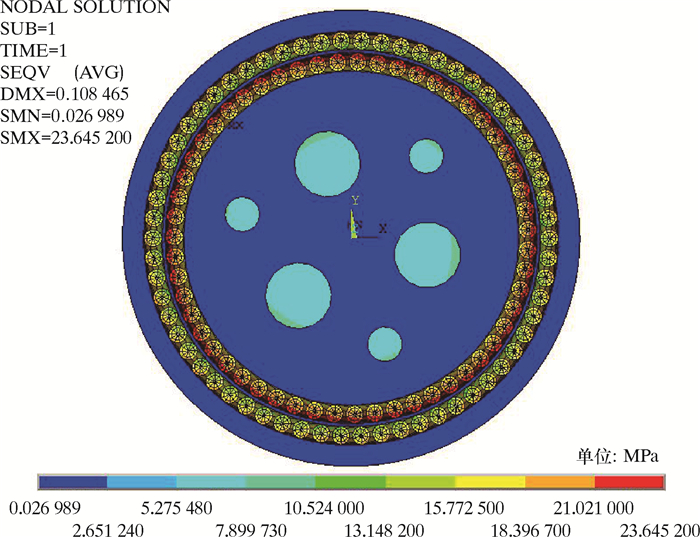
有限元解同Knapp解析解对比结果如表 3所示。有限元解与解析解相差很小,验证了笔者所建模型和接触设置的准确性。提取脐带缆模型的Mises应力,结果如图 4所示。由图 4可知,铠装钢丝应力明显大于直构件应力,其主要原因是铠装钢丝拉伸刚度大于直构件,铠装钢丝为脐带缆的主要承载单元。
| 材料 | 解析解/108N | 有限元解/108N | 误差/% |
| 刚性材料 | 4.99 | 4.96 | 0.6 |
| 不可压缩材料 | 4.80 | 4.96 | 3.3 |
|
| 图 4 脐带缆端部截面Mises应力 Fig.4 Mises stress on the umbilical cross-section |
2.3 基于弯曲刚度的模型验证
由于Witz解析模型未考虑摩擦,笔者首先将有限元模型中的摩擦因数设置为0,计算无摩擦时模型的弯曲刚度,然后同解析解对比以验证模型的可靠性。
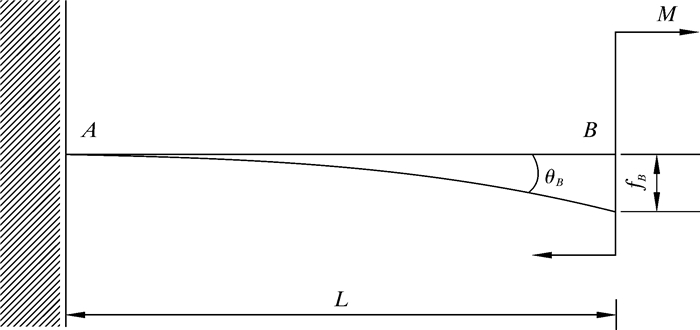
纯弯曲梁模型如图 5所示。模型一端固定、一端受弯,结合材料力学纯弯曲梁理论,可知弯矩作用下模型的弯曲刚度为:
|
| 图 5 纯弯曲梁模型 Fig.5 Model of the pure bending beam |
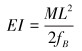
|
(6) |
式中:M为端部弯矩载荷,EI为结构的弯曲刚度,fB为端部挠度。
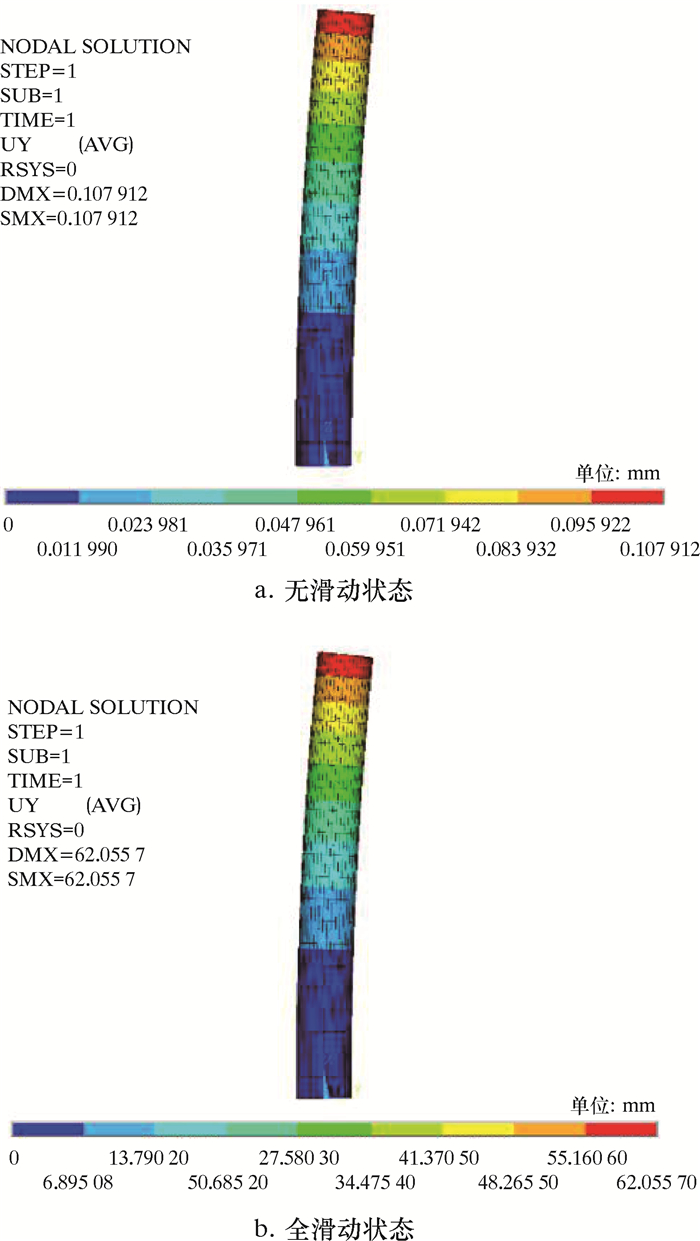
在有限元模型一端施加全约束,另一端施加不同弯矩以模拟无滑动状态和全滑动状态,求解并提取模型在无滑动状态和全滑动状态下自由端的挠度,结果如图 6所示。
|
| 图 6 脐带缆端部挠度 Fig.6 The deflection of the umbilical end |
将端部挠度和弯矩载荷等数据代入式(6)计算各模型弯曲刚度,并与解析解对比,结果如表 4所示。由表 4可知,不考虑摩擦,全滑动状态下脐带缆弯曲刚度解析解和有限元计算结果趋势一致,验证了笔者所建模型和接触设置的准确性。全滑动状态时解析解与有限元解基本一致,但无滑动状态下弯曲刚度差异较大,该状态下有限元解会低估其弯曲刚度。
| 状态 | 解析解/(kN·m2) | 有限元解/(kN·m2) | 误差/% |
| 无滑动状态 | 566.5 | 463.3 | 18.2 |
| 全滑动状态 | 40.7 | 40.3 | 1.0 |
3 脐带缆截面力学性能的参数敏感性分析
通过拉伸刚度、弯曲刚度有限元解与解析解的对比验证了所建有限元模型的准确性。上述脐带缆截面力学性能解析模型中,钢丝缠绕角度和钢丝直径等参数对其性能有影响,但上述解析模型忽略内部构件间的摩擦,因此无法考虑摩擦对截面力学性能的影响。此外,外压的改变会引起脐带缆最大静摩擦力的变化,进而影响其截面力学性能。基于此,笔者分别基于钢丝缠绕角度、钢丝直径、摩擦因数以及外压等因素对脐带缆力学性能进行参数敏感性分析。模型一端设置全约束,另一端施加外载荷且不限制扭转。
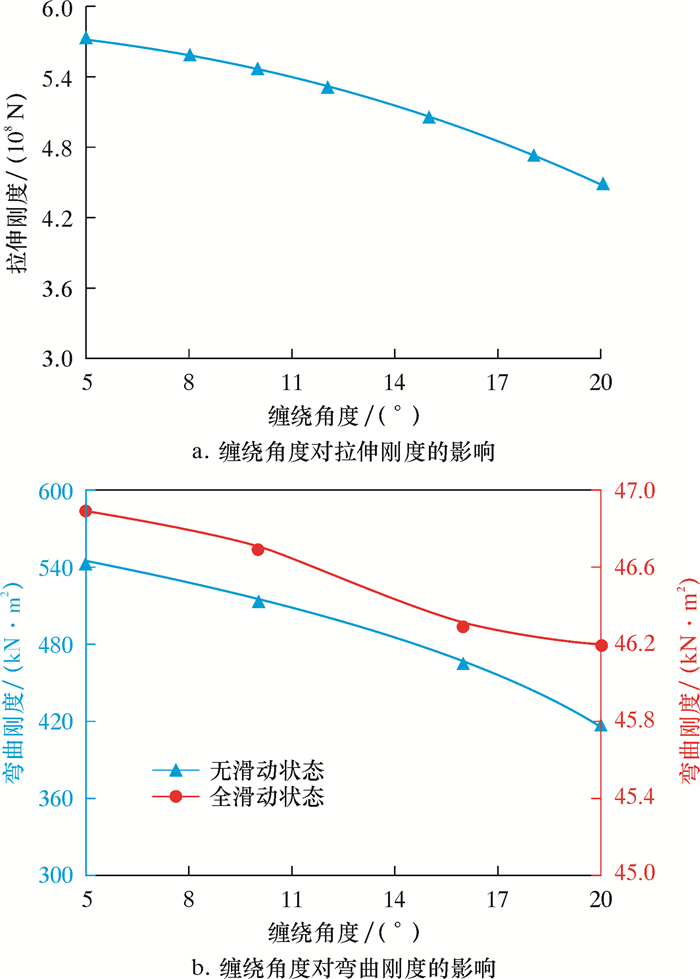
3.1 钢丝缠绕角度铠装钢丝层为螺旋缠绕结构,缠绕角度介于5°~25°之间。为控制变量,钢丝直径设置为5 mm,摩擦因数为0.1,外压为0 MPa,缠绕角度考虑从5°~20°变化,基于APDL语言计算得到缠绕角度对其刚度影响,结果如图 7所示。由图 7可知:钢丝缠绕角度越大,脐带缆的拉伸刚度越小,拉伸性能越差;弯曲刚度随钢丝缠绕角度的增大而减小,使其柔度上升。因此在保证拉伸性能满足使用条件下适当增大缠绕角度,可增加脐带缆的柔性。
|
| 图 7 缠绕角度对脐带缆截面力学性能的影响 Fig.7 Effect of helix angle on the mechanical properties of umbilical cable section |
3.2 钢丝直径
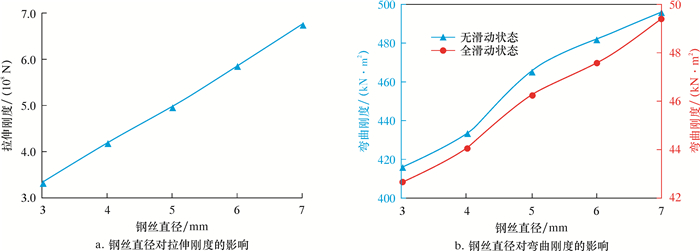
讨论钢丝直径对脐带缆力学性能的影响时,钢丝绳缠绕角度设置为16°,摩擦因数为0.1,外压为0 MPa,钢丝直径变化范围为3~7 mm,计算结果如图 8所示。由图 8可知:铠装钢丝的直径越大,脐带缆拉伸刚度越大;直径增大,脐带缆的弯曲刚度也随之增大,使其柔度下降。因此,在脐带缆拉伸刚度满足设计要求的前提下,钢丝绳的直径不宜过大。
|
| 图 8 钢丝直径对脐带缆截面力学性能的影响 Fig.8 Effect of wire diameter on the mechanical properties of umbilical cable section |
3.3 摩擦因数
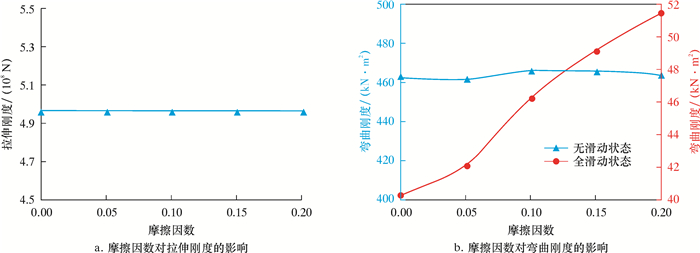
利用有限元模拟讨论脐带缆内部构件间摩擦对脐带缆力学性能的影响,钢丝绳缠绕角度设置为16°,钢丝绳直径5 mm,外压0 MPa,摩擦因数为0.0~0.2,计算结果如图 9所示。由图 9可知:脐带缆的拉伸性能与脐带缆内部摩擦基本无关;全滑动状态时,脐带缆弯曲刚度随摩擦因数的增大而增加。因此,减小构件间摩擦可在一定程度上保证脐带缆的柔性。
|
| 图 9 摩擦因数对脐带缆截面力学性能的影响 Fig.9 Effect of friction factor on the mechanical properties of umbilical cable section |
3.4 外压
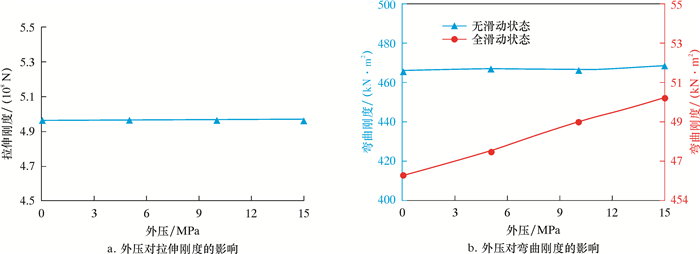
讨论外压对于脐带缆力学性能的影响时,钢丝绳缠绕角度设置为16°,钢丝绳直径5 mm,摩擦因数0.1,外压由0 MPa增加到15 MPa,计算结果如图 10所示。
|
| 图 10 外压对脐带缆力学性能的影响 Fig.10 Effect of external pressure on the mechanical properties of umbilical cable |
同摩擦因数对脐带缆拉伸刚度的影响类似,外压的改变不会引起其拉伸刚度的变化。无滑动状态阶段,脐带缆的弯曲刚度基本不随外压变化;全滑动状态阶段,脐带缆弯曲刚度随外压的增加而增大。因此,脐带缆作业状态下,需要考虑不同深度水压对脐带缆弯曲性能的影响。
4 结论基于ANSYS对脐带缆进行有限元分析,分别采用梁单元和实体单元模拟铠装钢丝和直构件,设置线线接触、线面接触模拟构件之间的接触摩擦,并计算脐带缆的拉伸刚度和弯曲刚度,得到以下结论:
(1) 解析模型无法考虑构件内部摩擦,难以精确描述脐带缆内部相互作用,有限元模拟能更准确地描绘脐带缆的变形和应力分布。
(2) 脐带缆主要承载部件为铠装钢丝。脐带缆力学性能不仅受钢丝缠绕角度和钢丝直径参数影响,摩擦因数和外压等参数的影响同样不可忽略。在脐带缆结构设计及强度优化时应考虑摩擦和外压等参数的影响。
(3) 脐带缆弯曲性能与外压有关,对作业状态下的脐带缆进行动力响应分析时,需要考虑水压对脐带缆弯曲性能的影响。
| [1] |
KNAPP R H. Structural modeling of undersea cables[J]. Journal of Offshore Mechanics and Arctic Engineering Transactions of the ASME, 1989, 111: 323-330. DOI:10.1115/1.3257102 |
| [2] |
KNAPP R H, DAS S. Finite element stress analysis of cables[C]//Oceans'99. MTS/IEEE. Riding the Crest into the 21st Century, [S.l.]: IEEE, 1999: 1026-1033.
|
| [3] |
KNAPP R H. Structural analysis of composite umbilical cables[C]//International Society of Offshore and Polar Engineers. Lisbon: [s.n.], 2007: 3487-3491.
|
| [4] |
DIXON M A J, ZHAO T. 3D modeling improves deepwater umbilical design dependability[C]//Offshore Technology Conference, [S.l.]: OTC, 2008.
|
| [5] |
LECORRE V, PROBYN I. Validation of a 3-dimensional finite element analysis model of a deep water steel tube umbilical in combined tension and cyclic bending[C]//Proceedings of the 28th International Conference on Offshore Mechanics and Artic Engineering, Honolulu: [s.n.], 2009: 120-128.
|
| [6] |
MERINO H, SOUSA J R, MAGLUTA C, et al. Numerical and experimental study of a flexible pipe under torsion[C]//ASME 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai: [s.n.], 2010: 911-922.
|
| [7] |
SæVIK S, GJøSTEEN J K. Strength analysis modelling of flexible umbilical members for marine structures[J]. Journal of Applied Mathematics, 2012(2): 50-68. |
| [8] |
杨志勋.脐带缆结构设计与分析方法研究[D].大连: 大连理工大学, 2012. YANG Z X. Investigation of structural design and analysis method for umbilical cable[D]. Dalian: Dalian University of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10141-1012393964.htm |
| [9] |
卢青针, 肖能, 阎军. 钢管脐带缆弯曲刚度有限元分析[J]. 计算机辅助工程, 2011, 20(2): 16-19. LU Q Z, XIAO N, YAN J. Finite element analysis on bending stiffness of steel tube umbilical cable[J]. Computer Aided Engineering, 2011, 20(2): 16-19. DOI:10.3969/j.issn.1006-0871.2011.02.004 |
| [10] |
肖能, 阎军, 卢青针, 等. 钢管脐带缆拉伸行为的有限元分析[J]. 油气储运, 2012, 31(3): 199-202. XIAO N, YAN J, LU Q Z, et al. Finite element analysis for steel tube umbilical cable under axial tension[J]. Oil & Gas Storage and Transportation, 2012, 31(3): 199-202. |
| [11] |
李伟民, 郭海燕, 牛建杰, 等. 海洋动态缆的截面布局及数值模拟研究[J]. 中国海洋大学学报(自然科学版), 2016, 46(8): 131-136. LI W M, GUO H Y, NIU J J, et al. The sectional layout and numerical simulation study of marine dynamic cables[J]. Periodical of Ocean University of China, 2016, 46(8): 131-136. |
| [12] |
KNAPP R H. Derivation of a new stiffness matrix for helically armoured cables considering tension and torsion[J]. International Journal for Numerical Methods in Engineering, 1979, 14(4): 515-529. DOI:10.1002/(ISSN)1097-0207 |
| [13] |
WITZ J A, TAN Z. On the flexural structural behaviour of flexible pipes, umbilicals and marine cables[J]. Marine Structures, 1992, 5(2): 229-249. |


