2. 中油国际(乍得)有限责任公司;
3. 中国石油大学(北京)
2. Petrochina International (Chad) Co., Ltd.;
3. China University of Petroleum(Beijing)
0 引言
可膨胀波纹管(以下简称波纹管)是一种截面呈波纹状的特殊管材,通过对圆管进行冷压加工,使圆管径向发生大的塑性变形而成,主要用于钻井过程中封堵各种复杂地层、补贴修复套管、作为井筒的封隔器以及延长技术套管长度等[1-3]。相对于圆形截面,加工后的波纹状截面可减小管体外径,使其通过上层套管或裸眼顺利到达封隔地层位置,随后借助液压将管体胀大并贴合井壁。
常见的波纹管截面形状为8字形,内部通径较小,无法安装井下工具串。随着波纹管技术的进步,施工工艺要求井下工具串能够安装于波纹管内部,故需重新设计截面,以增大内部通径。目前,波纹管截面的设计方法主要基于工程师的既有经验,结合绘图软件反复试算获得图形解。这种方法效率不高,缺乏对计算结果的评估环节,且精度和稳定性也不高。为解决上述问题,笔者提出一种波纹管截面设计计算和结果校验的系统方法。
1 波纹管截面形状设计基本要求多瓣波纹管一般由无缝钢管冷压制成,截面形状多为8字形、4瓣、6瓣、8瓣、10瓣结构,花瓣为波峰,2个花瓣之间的弧线为波谷。波峰与波谷之间一般由直线段连接,特殊情况下,直线段退化为一个点,波峰和波谷直接相连。波峰和波谷结构沿圆周方向呈周期性重复。为简化模型,对无缝钢管和成型后的波纹管做如下假设:
(1) 圆管截面周长与成型后的波纹管截面周长相等;
(2) 波纹管截面为轴对称图形;
(3) 波纹管截面轮廓由圆弧和切线或全部由圆弧组成;
(4) 波纹管加工过程中壁厚不变。
此外,成型后的波纹管还需满足相应的设计条件,主要包括:①最大外径应小于井筒直径,以便下入井筒中。②波纹管内部通径应大于工具串的外径,以便安装工具串。③波纹管膨胀后应实现尽可能小的椭圆度和残余应力,以满足加工和应用的可行性。④波纹管应满足抗内压和抗外挤强度要求。
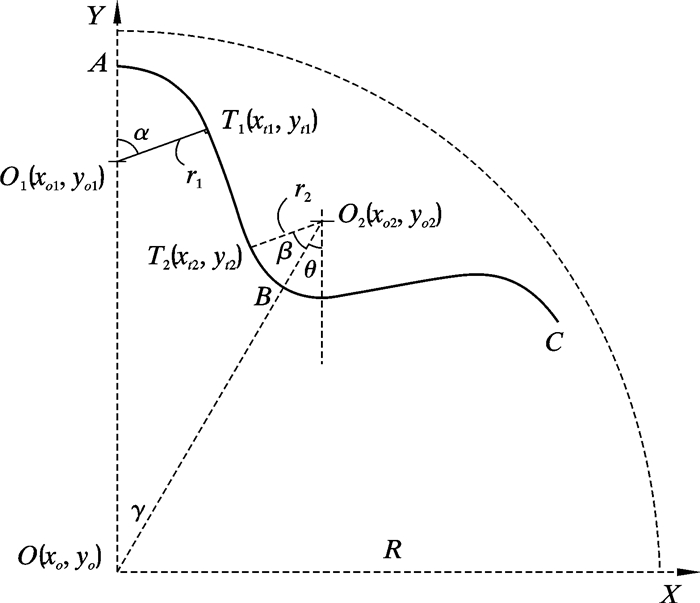
2 模型与算法 2.1 几何控制条件理论上,波纹管可根据需要设计为任意瓣。以n瓣波纹管截面为研究对象,忽略壁厚,仅考虑截面外轮廓;由于截面包含n个周期元素,取任一周期简化为图 1所示的几何模型,建立以点O(xo, yo)为原点的直角坐标系。O点为无缝钢管的截面圆心,O1点和O2点分别为波峰和波谷位置的圆弧所在的圆心,半径分别为r1和r2。T1和T2为切点,直线T1T2为圆O1和圆O2的内公切线。
|
| 图 1 波纹管截面几何模型 Fig.1 Geometry model of the expansion bellows cross-section |
几何控制条件如下。
圆心O1在y轴上,即有:
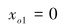
|
(1) |
圆心O2在过原点斜率为cotγ的直线上,即有:
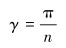
|
(2) |
弧线AC长度的n倍与加工前无缝钢管的周长相等,即有:
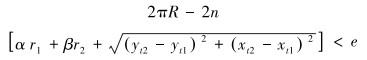
|
(3) |
式中:α为波峰圆弧的圆心角,rad;β为波谷圆弧圆心角,rad;r1为波峰圆弧半径,mm;r2为波谷圆弧半径,mm;e为偏差值,mm,该值趋近于0。
波纹管外包络圆直径小于给定值,即有:
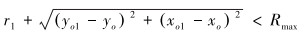
|
(4) |
式中:Rmax为限定的最大外径,mm。
波纹管内包络圆直径大于给定值,即有:
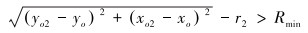
|
(5) |
式中:Rmin为限定的最小外径,mm。
r1和r2大于管材最小折弯半径rmin[2],即r1>rmin, r2>rmin,于是有:
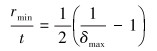
|
(6) |
式中:rmin为最小弯曲半径,mm;t为壁厚,mm;δmax为材料的伸长率。
需指出,切点T1和T2可重合,即直线T1T2退化为一个点,此时曲线AC由两段相切的圆弧构成。
2.2 截面形状设计流程常用设计方法的主要步骤如下。
(1) 依经验数据在Y轴适当位置绘制圆O1;
(2) 绘制直线OO2;
(3) 凭经验在直线OO2适当位置绘制圆O2;
(4) 绘制圆O1和圆O2内公切线;
(5) 阵列形成截面轮廓,计算周长;
(6) 若算得周长与下料管周长偏差较小,则计算终止,否则,重复步骤(2)~(6)。
这种方法着眼于几何图形,以图线交点求解坐标值。求解涉及的未知参数多达6个,且相互制约,计算难以快速收敛,过程繁琐,效率不高,精度难以保证。这种方法通常需6~8 h获得一个较为理想的解。若改变波纹管瓣数和最大允许外径等参数,则需重建模型,再次计算。
笔者提出一套新的算法,具体步骤如下:
(1) 根据限定条件估算切点T1坐标;
(2) 估算切点T2坐标;
(3) 由切点T1和T2作垂线,获圆心O1和O2;
(4) 阵列形成截面轮廓,计算轮廓周长;
(5) 若计算的周长与圆管周长误差较小,则计算终止,否则,重复步骤(1)~(4)。
新方法着眼于图形的几何关系,以切点为计算基点,未知数降为4个。基于这一方法,笔者编制了Matlab计算程序,实现了所需的计算功能。该方法可任意设置波纹管瓣数、计算精度和最大允许外径等参数,输入程序后由计算机给出数值解。初步测试中,程序可在8 min内获得10瓣结构的切点坐标数值解。
3 截面结构评估方法采用新算法和程序通常可以获得成千上万组解,有必要设置限定条件,筛选最为合理的解。考虑加工因素,r1和r2尽量取整,则剩余解的数量一般可降为数十组。采用ANSYS软件仿真分析波纹管膨胀过程,从膨胀作用力大小和膨胀后的管截面规则程度等角度进一步缩减解的数量,最终获得较为理想的有限组解。具体方法表述如下。
3.1 有限元分析采用ANSYS软件二维分析功能,选择单元Plane183,材料参数:弹性模量210 GPa,泊松比0.3,屈服强度270 MPa,切线模量5 GPa。建立模型并划分网格,施加位移约束。考虑波纹管的膨胀过程与时间相关,故在波纹管内表面施加30 s时间步载荷,步长0.5 MPa/s,最终压力26 MPa。
3.2 椭圆度评估膨胀后的波纹管椭圆度计算式为:
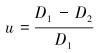
|
(7) |
式中:u为椭圆度;D1为波纹管的水平外径,mm;D2为波纹管的垂直外径,mm。
椭圆度越小,意味着膨胀后的波纹管截面越接近圆形,成型效果越好。
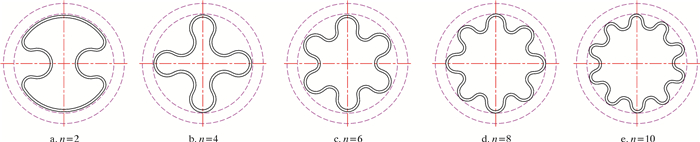
4 截面结构优化一般原则 4.1 多瓣结构选择图 2为截面周长相等、但瓣数不同的波纹管截面示意图。以椭圆度为主要衡量指标,考察同一内压下不同瓣数波纹管的膨胀效果,结果如图 3所示。
|
| 图 2 不同瓣数波纹管截面示意图 Fig.2 Cross section of the expansion bellows with different lobes |
|
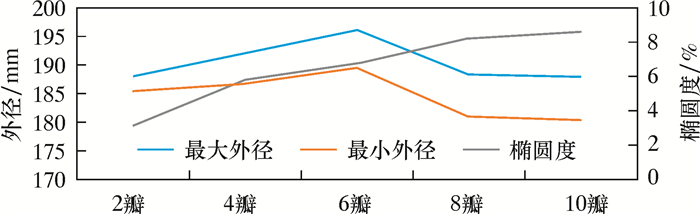
| 图 3 不同规格波纹管膨胀后的椭圆度 Fig.3 Ellipticity of the expansion bellows with different specifications after expansion |
由图 3可以看出,随着瓣数的增加,椭圆度由3%增加至8%以上,呈持续上升趋势。这说明瓣数越多,波纹管膨胀后的截面越不规则。进一步考虑膨胀后波纹管的最大外径和最小外径,发现图线在6瓣结构处出现拐点,即同样内压作用下,6瓣波纹管的外径最大。4瓣结构膨胀后外径仅次于6瓣结构。8瓣和10瓣最大外径相近,但明显小于6瓣结构。综合看来,6瓣结构最为合理。
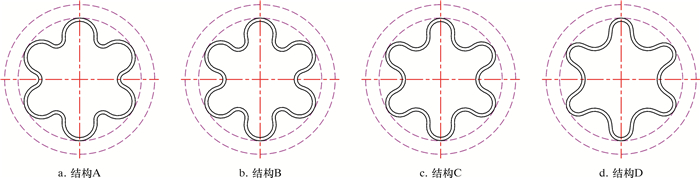
4.2 最优峰谷尺寸选择6瓣截面、周长相等的波纹管仍可选择多种波峰和波谷组合,如图 4所示。为寻求不同峰谷结构对膨胀效果的影响,选择4种6瓣波纹管结构进行仿真分析,其中结构A波峰半径16 mm,波谷半径10 mm;结构B波峰半径15 mm,波谷半径11 mm;结构C波峰半径14 mm,波谷半径13 mm;结构D波峰半径13 mm,波谷半径15 mm。
|
| 图 4 不同参数的6瓣波纹管结构示意图 Fig.4 Structural schematics of the 6-lobe expansion bellows with different parameters |
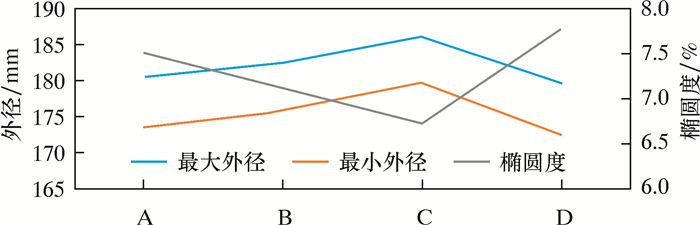
对比分析了4种峰谷尺寸组合的波纹管截面膨胀后的最大外径、最小外径和椭圆度,膨胀后外径尺寸如图 5所示。由图 5可知,结构C的最大外径最大,同时椭圆度最小。结构B的相关参数指标仅次于结构C。考虑4种结构的主要区别在于波峰和波谷直径不同,峰谷的比值分别为1.60、1.36、1.07和0.87,据此判断,波峰与波谷的半径比值越接近1,膨胀后的椭圆度越低,最小外径越大。
|
| 图 5 不同参数6瓣波纹管的椭圆度 Fig.5 Ellipticity of the 6-lobe expansion bellows with different parameters |
4.3 潜在应力集中区域
波纹管膨胀过程相当于对自身的二次加工,成型后的近似圆管内、外表面均存在残余应力[4-6]。仿真分析结果表明:膨胀后的波纹管应力主要集中于原波峰内侧和波谷外侧;应力值与波纹管截面形状有关[7-11],瓣数越多,残余应力分布越密集。
陈晓君等[5]对波纹管进行了破坏试验,试验中发现超过90%的撕裂点发生于波纹管波峰位置,该位置与残余应力集中区域吻合。残余应力的集中现象应引起足够重视,尤其在加工过程中应避免波峰位置存在气孔或损伤等缺陷。
5 波纹管设计应用算例 5.1 基本设计要求圆管外径245 mm,壁厚9 mm,要求加工后的波纹管最大外径小于215 mm,最小通径大于100 mm。
5.2 数值计算及最优解筛选设计时首先考虑采用6瓣结构,并据此估算切点T1横坐标XT1=[10,35],纵坐标YT1=[55,110];切点T2在切点T1的右下方,估算T2横坐标XT2= [11,60],纵坐标YT2= [55,100]。以上取值可根据实际情况扩大范围,该范围仅影响运算速度,不影响最终结果。
将波纹管波峰数、最大外径、最小内径、误差容许阈值以及估算的切点坐标范围等数据输入Matlab程序,经5 min左右运算,程序以数列形式计算出切点T1和T2的上百组精确坐标,并根据峰谷尺寸选择依据推荐最优解。在上述算例中,计算误差小于10-3 mm,推荐解为:XT1=20, YT1=85;XT2=21, YT2=71。
5.3 几何构图与截面设计在CAD软件中建立OXY平面坐标系,在第一象限中由原点绘制一条与Y轴成30°的斜直线L,那么圆心O1和圆心O2分别位于Y轴与直线L上。确定切点T1和T2,连接二点得直线段LT。在切点T1处作垂直于LT的直线Lo1,与Y轴交点即圆心O1;在切点T2处作垂直于LT的直线Lo2,与斜直线L交点即圆心O2。以O1T1为半径绘制Y轴与LT之间的圆弧;以O2T2为半径绘制LT与L之间的圆弧。至此完成1/12波纹管外形轮廓的绘制,采用阵列或镜像等方法即可完成完整曲线的绘制。
根据假设,圆管加工过程中壁厚保持9 mm不变,据此完成本例波纹管形状设计。实测其最大外径207.2 mm,最小内径107.6 mm,满足设计要求。
6 结论及认识(1) 建立了一套用于可膨胀波纹管截面设计的新方法。该方法建立了基本假设,抽象出几何模型,通过数值计算获得关键设计参数,结合仿真模拟优选出最优设计方案。相对于基于图形的试算方法,新方法提高了设计效率,增强了计算结果的稳定性。
(2) 通过对比分析,获得多瓣波纹管截面设计的主要原则:在给定的内、外径约束条件下,6瓣截面较为理想;对于6瓣结构的波纹管,波峰和波谷半径比接近1时,截面最容易还原为圆形。
(3) 波纹管膨胀后残余应力主要集中于波峰处,加工过程中应避免波峰处的质量缺陷,产品检验过程中应特别注意检查这一位置。
| [1] |
郭慧娟, 王辉, 耿莉, 等. 可膨胀波纹管有限元分析与现场应用[J]. 石油机械, 2008, 36(9): 99-101. GUO H J, WANG H, GENG L, et al. Finite analysis and field application of expandable convoluted tubes[J]. China Petroleum Machinery, 2008, 36(9): 99-101. |
| [2] |
官英平, 李洪波, 王凤琴. 板材弯曲最小相对半径计算方法探讨[J]. 金属成形工艺, 2003, 21(5): 52-53. GUAN Y P, LI H B, WANG F Q. Discussion about calculation methods of the minimum relative bending radius for plate bending[J]. Metal Forming Technology, 2003, 21(5): 52-53. DOI:10.3969/j.issn.1674-6457.2003.05.019 |
| [3] |
韩建增, 张先普. 残余应力对套管抗挤强度影响的有限元分析[J]. 钻采工艺, 2001, 24(2): 41-43. HAN J Z, ZHANG X P. Effects of residual stress on casing collapse resistance[J]. Drilling & Production Technology, 2001, 24(2): 41-43. |
| [4] |
涂玉林, 杨红歧, 胡彦峰, 等. 膨胀波纹管在小井眼的安全应用工况模拟试验研究[J]. 石油钻探技术, 2018, 46(2): 70-75. TU Y L, YANG H Q, HU Y F, et al. Simulation and experimental study on the safe application condition of expandable profile liner in slim holes[J]. Petroleum Drilling Techniques, 2018, 46(2): 70-75. |
| [5] |
陈晓君, 宋刚, 孟庆鸿, 等. 小口径勘探用可膨胀波纹管ANSYS模拟与实验分析[J]. 探矿工程, 2014, 41(11): 37-41. CHEN X J, SONG G, MENG Q H, et al. ANSYS simulation of expandable convoluted tubing for small diameter bore prospecting and experimental analysis[J]. Exploration Engineering, 2014, 41(11): 37-41. DOI:10.3969/j.issn.1672-7428.2014.11.012 |
| [6] |
尹飞, 高宝奎, 张进, 等. 油井堵漏可膨胀波纹管的有限元分析[J]. 石油机械, 2012, 40(5): 66-69. YIN F, GAO B K, ZHANG J, et al. Finite element analysis of the expandable bellows for oil well plugging[J]. China Petroleum Machinery, 2012, 40(5): 66-69. |
| [7] |
刘晓丹, 陶兴化, 韩振强, 等. 振动时效工艺在消除膨胀波纹管残余应力中的应用[J]. 振动与冲击, 2015, 34(4): 171-174. LIU X D, TAO X H, HAN Z Q, et al. Application of vibratory stress relief in relaxation of residual stress for expandable corrugated liners[J]. Journal of Vibration and Shock, 2015, 34(4): 171-174. |
| [8] |
SANG Z F, ZHU Y Z, WIDERA G E O. Reliability factors and tightness of tube-tubesheet joints[J]. ASME Journal of Press Vessel Technology, 1996, 118(5): 137-141. |
| [9] |
MEHRABADI S J, AZIZMORADI M, EMAMI M M. Stress relief and material properties improvement trough vibration vs. common thermal method[J]. Journal of Solid Mechanics, 2012, 4(2): 170-176. |
| [10] |
KOHLPAINTNER W R. Calculation of hydraulically expanded tube-to-tubesheet joints[J]. ASME Journal of Press Vessel Technology, 1995, 117(2): 24-30. |
| [11] |
GOODIER J N, SCHOESSOW G J. The holding power and hydraulic tightness of expanded tube joints:analysis of the stress and deformation[J]. ASME Journal of Press Vessel Technology, 1943, 65(7): 489-496. |


