0 引言
在许多油气田,与开采和注水有关的储层压实一直被认为是导致套管损坏的一个主要原因[1-7]。高度可压缩储层中压实致套管变形的机理随井眼条件和套管性能的变化而变化。出砂或固井作业不理想导致套管无支撑,从而可能引起套管弯曲[8-9]。套管可能发生剪切变形,特别是靠近射孔套管的两端,这是因为射孔套管和完整套管之间存在刚度差异[8, 10-11]。在斜井中,由于储层和边界地层之间应变差异大,在储层边界最大弯曲应变的作用下,套管可能发生弯曲变形[3, 12]。压实致套管变形不仅限于储层,也可能发生在上覆地层中。由于拱效应和储层非均质性,储层压实通常不是均匀的,导致非均匀的储层表面下沉。非均匀变形能够引起上覆地层中或储层顶部附近沿弱层理面的局部剪切,从而可能导致套管剪切损坏[7-8, 10, 12]。
对所有这些与压实、套管弯曲有关的变形机理,特别是对在许多油田都能频繁观察到的邻近储层边界的套管变形研究很少。例如,没有简单的可用的方法确定斜井中弯曲应变的变化。为了量化井斜对套管变形的影响,用解析表达式预测储层压实引起的套管轴向应变εa[8, 12]:
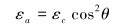
|
(1) |
式中:εc为储层压实应变,θ为井斜角。
式(1)是基于均匀储层压实的假设推导出来的。该式预测,在直井中,套管轴向应变与储层压实应变相等,且随着井斜的增大呈非线性减小。然而,因为轴向缩短不仅仅是适应储层压实应变的变形机理,所以该方程对预测邻近储层边界压实致套管应变相对有限。另外,通过该式还得知,套管直径/壁厚比(Diameter/Thickness,以下简称D/t)和屈服强度对套管轴向应变没有影响。然而,诸多研究表明,高屈服强度有助于防止套管变形[13-15],而且增大套管壁厚有助于增大套管横截面对非均匀载荷的阻力[16]。为了对比可供选择的套管设计的成本和优势,套管应变分析中需要考虑套管屈服强度和套管D/t对套管变形的影响。在设计阶段,对于不同的设计,为了优化井眼轨道和选择合适的套管,要求用井筒附近地带的3D地质力学模型定量评估真实储层条件下的套管应变。
为了简化套管变形分析,缩短分析时间,BP America公司和BP Exploration公司的研究人员使用有限元模型进行了一系列3D数值试验,根据储层衰竭压力大小和岩石压缩性量化了井斜、套管D/t比、套管屈服强度和压实应变对压实致邻近储层边界套管变形的影响。根据模拟结果推导出一个经验公式,以便能够代替预测压实致邻近储层套管应变的数值模型,从而满足工程应用。为了给我国的研究人员提供借鉴,推动套管变形损坏分析技术的发展,笔者对研究情况进行了介绍。
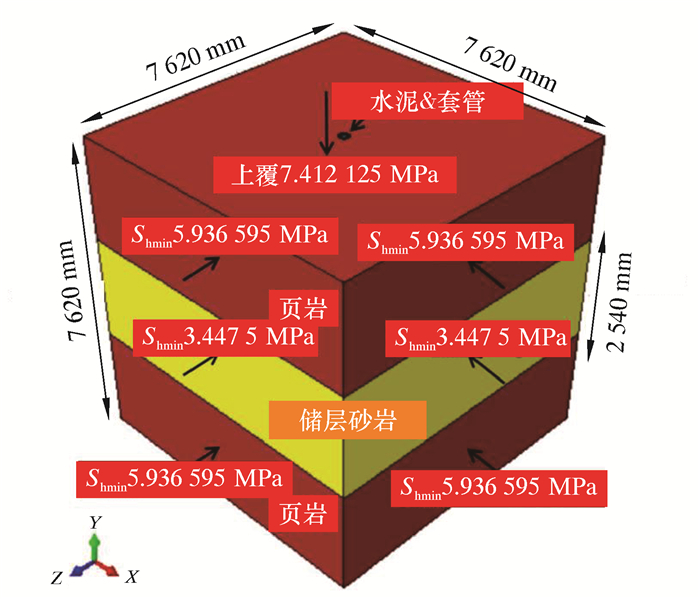
1 数值试验方法为了量化压实致邻近储层边界套管应变,构建了井筒附近地带3D有限元模型,以模拟由于孔隙压力下降引起的砂岩储层压实导致的套管变形。模型包括套管柱、岩石(储层砂岩和上下边界页岩)和水泥环(见图 1)。储层倾角0°,储层倾角方位0°,井眼井斜方位0°、22.5°、45.0°、67.5°和90.0°,井眼方位0°,井眼直径269.875 mm,套管外径219.075 mm,套管内径205.664、196.215和167.005 mm,套管直径/壁厚比32.67、19.17和8.41。为在不使用过多单元的情况下保持细网格,实现井筒处应力集中,设定模型尺寸小于现场尺寸,长、宽和高均为7 620 mm,砂层厚度为2 540 mm,与269.875 mm的井眼直径相比足够大,可避免影响结果的边缘效应。套管变形分析结果表明,与压实相关的套管应变是中心对称的。
|
| 图 1 井筒附近地带3D有限元模型 Fig.1 3D finite element model of the formation near wellbore |
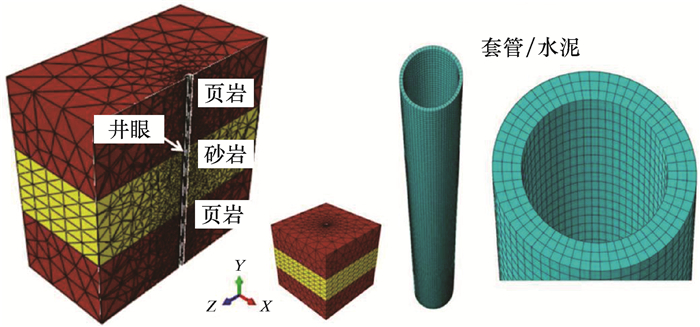
岩石、水泥和套管实现了有限元网格划分的独立化,并组合为一个整体,如图 2所示。
|
| 图 2 砂岩、页岩、水泥和套管网格 Fig.2 Mesh of sandstone, shale, cement and casing |
岩石网格划分采用四面体单元,而水泥和套管网格划分采用六面体单元。非结构化四面体单元使井眼周围的网格划分更为容易,而且还有助于远离井眼的单元尺寸逐渐增大,并使砂岩网格比页岩网格更细。另一方面,水泥环和套管采用非结构四面体单元利于确保通过壁厚的单元至少有3个,从而在储层砂岩压实过程中分解任何弯曲产生的应力。水泥和未射孔套管网格单元数量相同,利于网格节点完全对齐。
对于有限元模型中定义的各种材料,本构模型和参数值是必需的。套管采用弹塑性本构模型,最终屈服性能与所建模的各种类型的钢一致,塑性行为通过完全塑性的von Mises屈服准则结合相关的Prandtl-Reuss流动法则描述。假设水泥服从有光滑的流动势的屈服包络线,砂岩和页岩特性根据深水墨西哥湾可高度压缩的中新世砂岩和边界页岩的岩心试验数据定义。Drucker-Prager帽盖模型用于模拟与压力有关的储层砂岩的屈服行为。屈服面凝聚力为0.689 5 MPa,摩擦角为35°,该摩擦角类似于Mohr-Coulomb模型中的内摩擦角。帽盖长宽比为0.5,三轴拉伸屈服应力与三轴压缩屈服应力比为0.8。该砂岩模型定义了压实作用下可高度压缩岩石一般的应力应变行为,但是可能并不代表所有可压缩储层岩石。为了简化模型,分析中假设页岩保持弹性状态,未定义非弹性参数,有限元模型中定义的各种材料参数值见表 1。
| 材料 | 密度/(g·cm-3) | 弹性模量/MPa | 泊松比 | 凝聚力屈 服应力/MPa | 内聚力/MPa | 摩擦角/(°) | 膨胀角/(°) |
| 套管 | 8.0 | 206 160.5 | 0.30 | 275.8、620.6、930.8 | — | — | — |
| 水泥 | 1.8 | 9 308.3 | 0.18 | 103.4 | — | 10 | 5 |
| 页岩 | 2.3 | 3 447.5 | 0.45 | — | — | — | — |
| 砂岩 | 2.1 | 517.1 | 0.33 | 6.9 | 689.5 | 35 | — |
岩石有效应力状态和储层原始压力为:页岩顶部有效垂直应力7.412 1 MPa,页岩有效水平应力5.936 6 MPa,砂岩有效水平应力3.447 5 MPa,砂岩孔隙压力49.299 3 MPa,最大衰竭压力49.299 3 MPa。模型初始应力是根据深水墨西哥湾中新世砂岩应力测量定义的,最大水平应力值和方向未知。区域钻井经验表明,中新世砂岩储层应力状态接近于各向同性,因此假设最大水平应力与最小水平应力相等。压实开始前,可以忽略初始应力状态对套管变形的影响。因为储层压力衰竭过程中页岩孔隙压力预计不会改变,所以只定义了砂岩孔隙压力单元。对每个砂岩和页岩单元的有效水平应力进行了初始化和计算。为了平衡这些应力,施加有效上覆载荷至模型顶面,施加滑动边界条件至整个外边界,以防止模拟过程中的法向位移。在套管和水泥及水泥和地层之间无滑移的假设下运行该模型。因此,该模型代表了套管变形的最糟糕情形,即压实应变适应套管变形。另外,沿着砂岩-页岩界面不允许滑移,这是因为模型中没有考虑拱效应,储层砂岩是平的,经历了均匀压实。
采用ABAQUS进行有限元计算。在赋值上述特性、载荷、边界和初始条件后,设置初始地压平衡步骤。通过有限元求解步骤计算了平衡受边界条件和材料响应限制的初始应力和重力载荷的平衡应力状态。一旦达到与砂岩和页岩预期的地应力一致的平衡应力状态,那么接下来的分析步骤逐渐增大砂岩有效应力至49.299 3 MPa,相当于耗尽原始储层孔隙压力至0。在最大有效应力作用下,砂岩遭受了8.3%的压实。
为了捕捉邻近储层边界套管应变变化模式,在相同的边界和载荷条件下进行了一定井斜(0.0°、22.5°、45.0°、67.5°和90.0°)范围内的模拟。设定套管D/t为8.14、19.17和32.67,套管屈服强度为275.8、620.6和930.8 MPa。为了量化储层压实、井斜、套管D/t与屈服强度对套管应变的影响,共进行了55次数值试验。为便于区分这些数值试验,使用字母D代表井斜、R代表套管D/t、G代表套管屈服强度。每个字母后都跟着其代表的属性值,该值被四舍五入至其最近的整数,例如,D68R8G40指的是67.5°井斜的数值试验,套管D/t为8.14,套管屈服强度为275.8 MPa[21]。
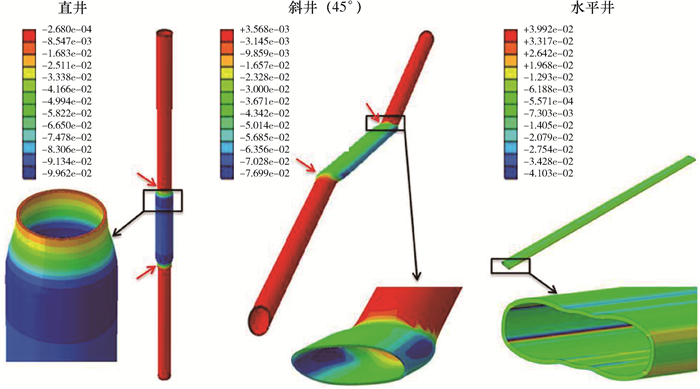
2 试验结果使用代表套管真实应变的对数应变对套管变形进行了量化(见图 3)。从图 3可以看出,49.299 3 MPa的压力衰竭后,储层压实致套管应变是中心对称的。虽然应变大小也随着压实应变、套管D/t和屈服强度的变化而变化,但应变模式和变形机理仅受井斜的影响。直井中储层砂岩内的套管变形主要为轴向缩短和径向膨胀。由于数值试验中均匀的储层压实和各向同性的水平应力状态设置,套管应变周向均匀。因为储层边界压实的变化,沿着砂岩和页岩界面(红色箭头所指位置)附近井眼的轴向缩短和径向膨胀不均匀,导致砂岩和页岩界面附近的应变最大。斜井中储层压实附近套管变形的特征是套管倾斜方向上的弯曲,最大弯曲应变总是集中在凹面区域。相比之下,在远离界面的储层砂岩中,套管变形表现为轴向缩短和截面椭圆形变化。因为在储层压实方向上套管变形达到最大,轴向缩短分量减少,而径向变形分量因井斜角增大而增大。因此,在水平井中,套管变形主要表现为顶部和底部的径向缩短与两侧的伸长。
|
| 图 3 直井、斜井和水平井井眼中压实致套管变形特征 Fig.3 Casing deformation characteristics by compaction in vertical, inclined and horizontal wellbores |
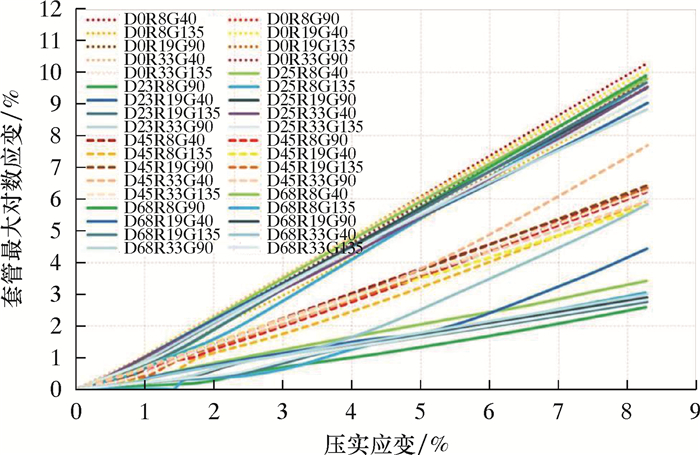
图 4显示了所有数值试验中邻近储层上边界的套管应变变化。套管变形以塑性屈服为特征,只有第一个0.3%或更少的应变表现为塑性变形。套管应变随压实应变以越来越快的速度呈非线性增长,例如,当压实应变小于1%时,D0试验中的套管应变小于压实应变,而当压实应变大于4%时,套管应变大于压实应变。该非线性增长趋势具有幂律的特点,在D68R33G40、D68R19G40和D45R33G40等3个试验中更为明显,表明在大斜度井中,当套管应变超过某个极限时,使用高套管D/t和低屈服强度套管可能加剧邻近储层边界套管变形。
|
| 图 4 邻近储层上边界套管应变与储层压实应变的关系 Fig.4 Relationship between casing strain at the upper boundary of adjacent reservoir and reservoir compaction strain |
对于某一给定的压实应变,套管应变大小主要受井斜影响(见图 4)。套管应变随井斜的增大而减小,但递减速度是变化的。在大多数试验中,套管应变随套管D/t比和屈服强度在一个狭窄的范围内变化,但是在套管D/t最大和屈服强度最低的D45和D68试验中,套管应变对套管特性非常敏感。套管应变随套管D/t和屈服强度的变化见图 5和图 6。由于D23和D0试验中套管应变随套管D/t和屈服强度的变化基本相同,为了避免曲线重叠,图中没有给出D23试验套管应变数据。
|
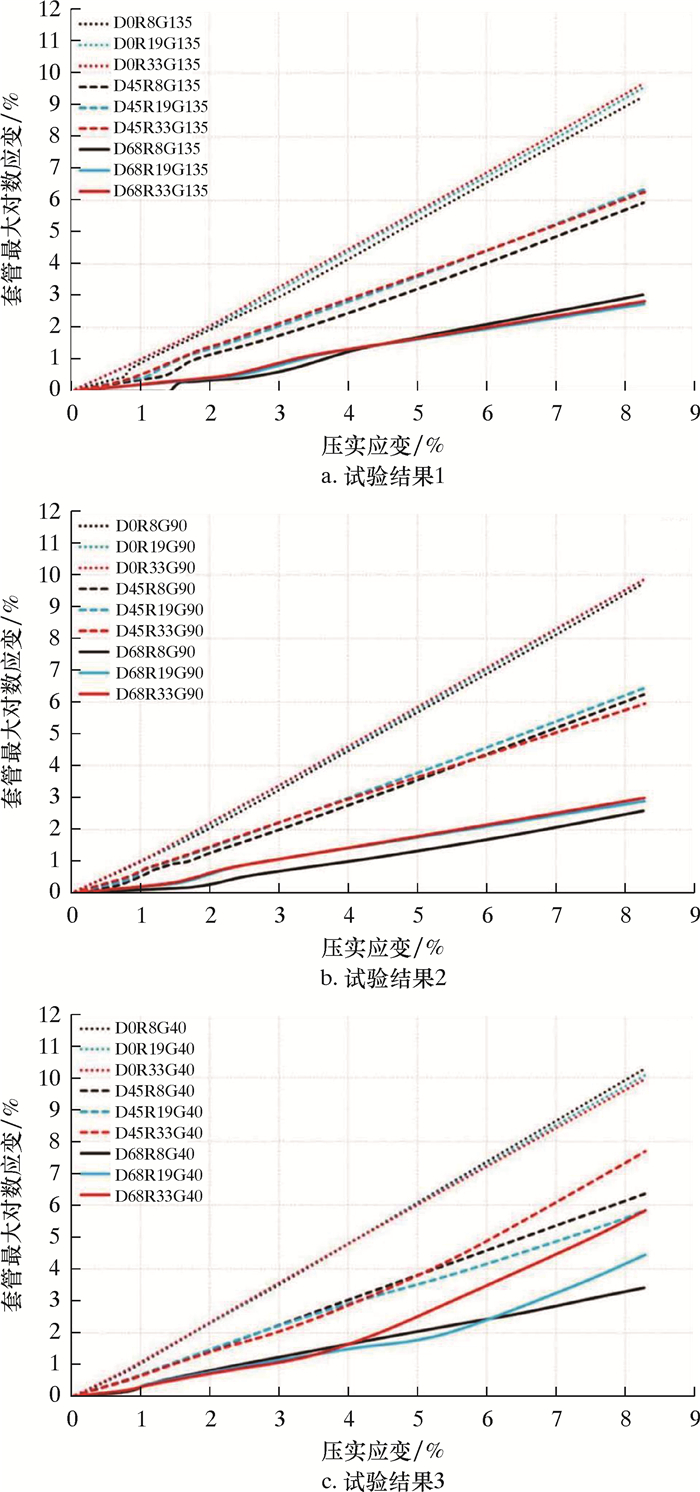
| 图 5 套管D/t对邻近储层边界套管应变的影响 Fig.5 Effect of casing D/t ratio on casing strain at adjacent reservoir boundary |
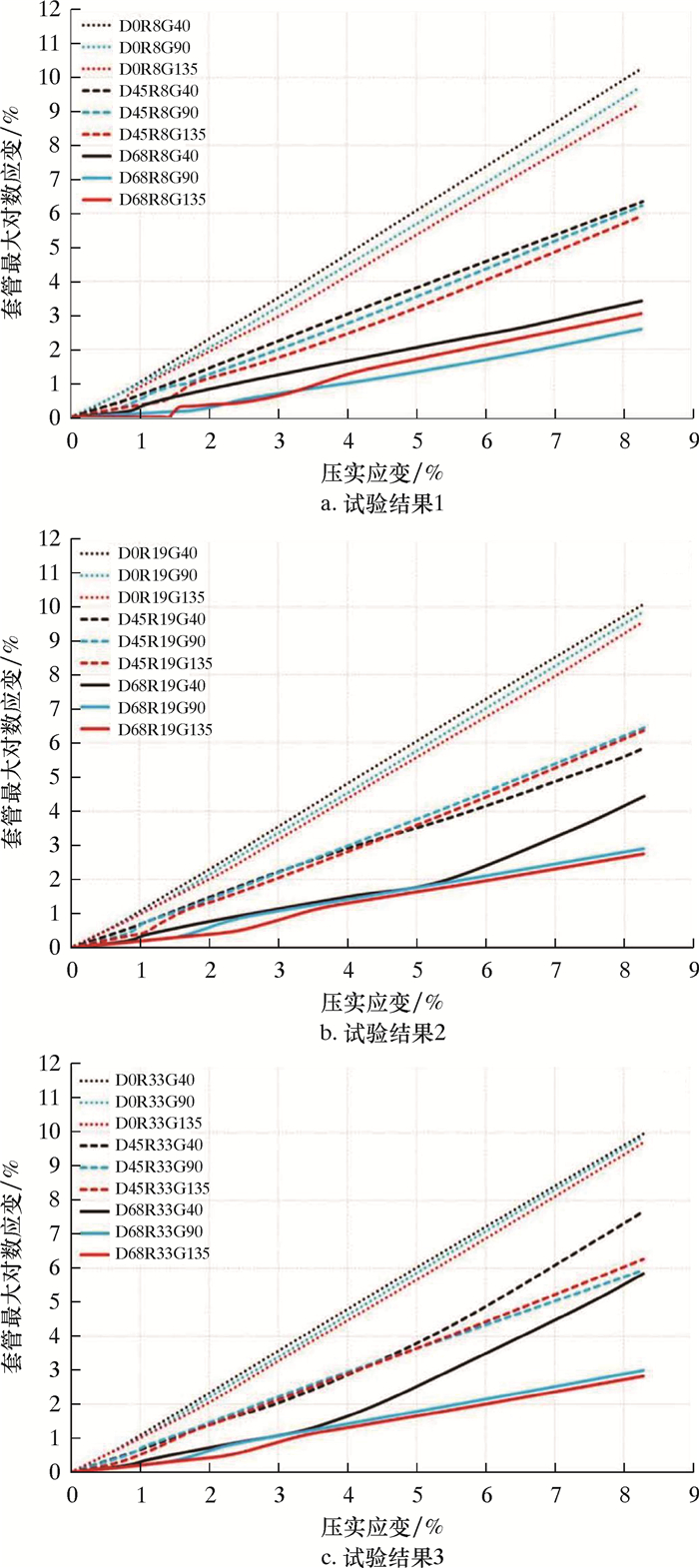
|
| 图 6 套管屈服强度对邻近储层边界套管应变的影响 Fig.6 strain at adjacent reservoir boundary |
与其他评价参数相比,套管D/t对套管应变的影响最小。除了预测相对较低套管应变的D45R8G135和D68R8G90试验以外,其他G135和G90试验中的套管应变受套管D/t的影响较小(见图 5a和图 5b)。在D0R33G135试验中,套管应变受套管D/t的影响也不大,但在D45R33G40、D68R33G40和D68R19G40试验中,套管应变在分别超过临界值5.0%、3.5%和5.3%后,随着压实应变以较高的速度增加(见图 5c)。可见低D/t的套管易于出现较小的应变,而对于小斜度井中壁更厚、屈服强度更高的套管,D/t对套管应变的影响微乎其微。但是在大斜度井中,如果套管屈服强度较低,高D/t套管的变形也可能加速。
与套管D/t相比,套管屈服强度对套管应变的影响更有规律、更显著(见图 6)。在D0和D45R8试验中,在套管D/t相同时,对于某一给定的压实应变和井斜,较高的套管屈服强度导致较低的套管应变(见图 6a)。虽然较高屈服强度的套管仍趋向于较小的变形,但在较大井斜或较高套管D/t的其他试验中该变化模式改变(见图 6b和图 6c)。如在D0试验中,随着套管D/t的增大,套管屈服强度对套管应变的影响变得不那么重要(见图 6a~图 6c虚线)。另外,在套管屈服强度相同时,对于某一给定的压实应变和井斜,D0G135试验中套管应变通常随着套管D/t的增大而减小,而D0G90和D0G40试验中套管应变随着套管D/t的增大而增大。
为了量化套管应变随评价参数的变化,根据图 4所示的套管应变预测结果构建了最佳拟合方程。因为最小化套管损坏风险时,套管弹性应变影响不大,所以忽略套管弹性应变,并假设在塑性屈服之前,套管应变以与套管塑性应变相同的幂律形式随着储层压实应变的变化而变化。因此,邻近储层边界套管应变的变化εb及储层压实应变εc仅通过幂律方程(2)定义,压实应变与储层衰竭压力大小Δp和储层岩石体积压缩系数Cb成正比,即:
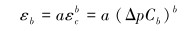
|
(2) |
幂律方程常数a和指数b分别由式(3)和式(4)给出:
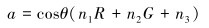
|
(3) |
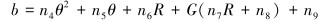
|
(4) |
式中:R为套管D/t,G为套管屈服强度,n1=0.005 4,n2=-0.002 1,n3=1.094 4,n4=-0.000 077 6,n5=0.003 89,n6=-0.003 6,n7=0.000 008,n8=0.000 4,n9=1.09[21]。
3 讨论与分析套管变形受数值模型边界和载荷条件的影响。模型中假设套管和水泥以及水泥和地层之间界面无滑移。邻近储层边界套管应变模型预测结果代表由于储层压实套管实际经历的最大可能应变。这是因为生产过程中很可能发生滑移,从而可能极大减小套管轴向应变[1]。在所有的斜井数值试验中,邻近储层边界套管变形具有套管倾斜方向弯曲的特征,最大弯曲应变总是集中在凹面区域,其原因是弯曲过程中水泥和地层约束造成套管内表面阻力比外表面阻力低。模拟中,初始地应力远小于套管屈服应力,因此对套管变形没有多大影响。
数值模型预测的邻近储层边界套管应变变化主要受储层压实和井斜大小影响。因为储层压实应变完全表现为套管变形,因此预测的套管应变随储层压实的增大而呈非线性增大(见图 4)。对于某一给定的压实应变,套管应变基本上是井斜的函数,这是因为套管载荷条件随着井斜的变化而变化:即对于直井来说,载荷是轴向压实的;对于斜井来说,载荷是轴向和横向组合压实的;对于水平井来说,载荷是横向压实的;对于相同的储层压实应变,横向压实作用下邻近储层边界套管比轴向压实作用下邻近储层边界套管的变形小(见图 3)。因此,预测的套管应变显示了随井斜增大而呈非线性减小的趋势,套管变形从轴向缩短和径向膨胀变为截面椭圆变形。
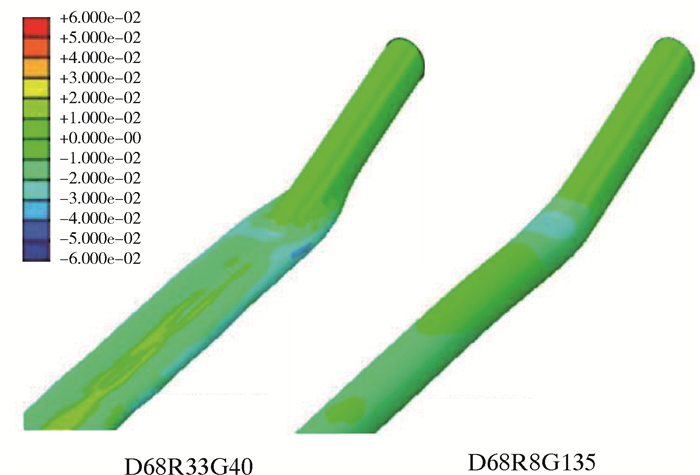
套管屈服强度和套管D/t对套管变形的影响是次要的。然而,在D45R33G40、D68R33G40和D68R19G40数值试验中,套管变形加速,与D45和D68数值试验(见图 4)相比,在储层压力完全衰竭后,具有高得多的应变特征。在模拟结束时,套管变形对比显示,与D68R8G135试验相比,D68R33G40试验中的套管经历了高得多的径向应变(见图 7)。因为这两个试验在相同的边界和载荷条件下进行,所以D68R33G40试验中强化的变形一定与较低的套管屈服强度和较高的套管D/t相关。D0试验中,在轴向压实载荷条件下套管变形,套管应变随着套管屈服强度的降低有规律增大(见图 6)。相反,套管应变随着套管D/t的增大有增大的趋势,但是在比较狭窄的范围内变化(见图 5)。另外,如在D45R33G40和D68R33G40试验中观察的那样,高套管D/t不会导致高应变,表明套管应变对套管屈服强度非常敏感,而对轴向压实载荷条件下的套管D/t不敏感。D68试验中,在轴向和横向压实载荷条件下套管变形。在较低的套管屈服强度和较高的套管D/t试验中,套管应变急剧减小,表明在横向压实载荷条件下,套管应变对套管屈服强度和套管D/t非常敏感。因此,在任何方向的井眼中,较高的套管屈服强度可能有助于降低压实致套管损坏风险,而在大斜度井中,壁较厚的套管可能会更有效地防止压实致套管损坏。
|
| 图 7 套管屈服强度和D/t对邻近储层上边界套管应变的影响 Fig.7 Effect of casing yield strength and D/t ratio on casing strain at the upper boundary of adjacent reservoir |
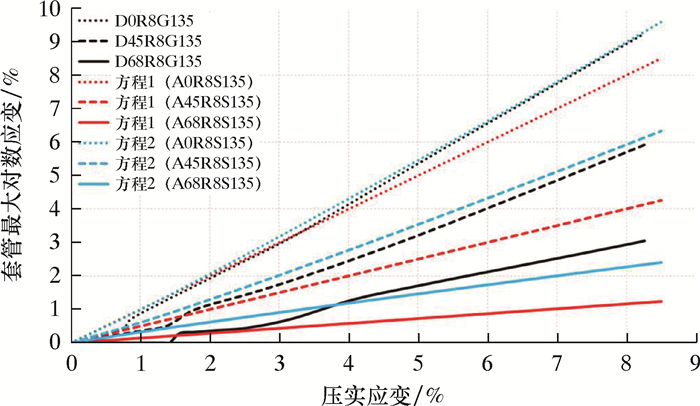
为了说明方程(2)对于评估套管应变的作用,将计算结果与井斜为0.0°、45.0°和67.5°的R8G135数值试验结果进行了对比(见图 8)。方程(1)预测的相应井斜的轴向应变叠置在图中,以强调解析模型和数值模型趋势之间的差异。对于直井来说,在塑性屈服之后,方程(2)应变预测结果与数值模型结果相匹配,最大差异小于5%。随着井斜的增大,方程(2)的应变预测结果已不够准确。方程(2)和数值模型之间的最大差异小于45°井斜的数值模型预测结果的10%,而可能大于井斜67.5°的数值模型预测结果的30%,这是因为套管应变对套管屈服强度和套管D/t的依赖性随着井斜的增大变得不那么有规律。对于45°井斜,如果套管D/t不太高、屈服强度不太低,那么数值模型预测8%的储层压实应变可能诱发6%或更少的邻近储层边界套管应变(见图 4),表明如果井斜大于45°且选择了合适的套管,那么邻近储层边界套管损坏影响不大。因此,方程(2)计算的小斜度井的应变对于工程应用来说是足够的。
|
| 图 8 方程(1)和方程(2)套管应变计算结果与有限元模型结果对比 Fig.8 Comparison of the calculation results and finite element model results of casing strain by equation (1) and equation (2) |
方程(1)表明,直井中最大套管轴向应变与储层压实应变相等。然而,数值试验结果显示,最大邻近储层边界套管应变小于套管钢材屈服之前的压实应变(见图 4和图 8),这是因为在弹性范围内,套管比岩石和水泥更硬。数值试验也显示,在套管屈服之后,邻近储层边界最大套管应变大于压实应变,这是因为压实应变不仅表现为相同数量的轴向缩短,而且还表现为径向膨胀。对于斜井来说,方程(1)计算的轴向应变远小于数值模型预测结果,这是因为数值模型允许考虑轴向和横向压实载荷作用下的最大应变,而方程(1)仅考虑轴向应变分量。
4 结束语有限元模拟显示,如果套管与水泥和水泥与地层之间的界面无滑移,那么压实致邻近储层边界套管应变随储层压力衰竭和岩石压缩性的增大以幂律形式增大。对于任何井斜来说,在套管塑性屈服开始之前,最大套管应变小于压实应变。然而,持续压实可能最终会导致套管应变大于储层压实应变,特别是在小斜度井中尤为如此。另外,套管变形机理和相关的套管载荷条件随井眼方向的变化而变化,所以预测的套管应变随井斜的增大呈非线性减小。与储层压力衰竭程度、岩石压缩性和井斜相比,套管屈服强度和D/t对套管变形的影响是次要的。在轴向和横向载荷条件下,套管屈服强度对套管应变的影响更有规律。当套管屈服强度增大时,套管应变减小。套管D/t对压实致套管变形的影响与套管载荷条件密切相关,在受轴向压实(小斜度井)的载荷条件下,套管应变随套管D/t的变化较小,而在受横向压实(大斜度井)的载荷条件下,套管变形随套管D/t的变化较大。
| [1] |
BRADLEY D A, CHIA Y P. Evaluation of reservoir compaction and its effects on casing behavior[R].SPE 14985, 1989.
|
| [2] |
VUDOVICH A, CHIN L Y, MORGAN D R. Casing deformation in ekofisk[J]. Journal of Petroleum Technology, 1989, 41(7): 729-734. DOI:10.2118/17856-PA |
| [3] |
BRUNO M S. Subsidence-induced well failure[R].SPE 20058, 1990.
|
| [4] |
SILVA F V, DEBANDE G F, PEREIRA C A.Casing collapse analysis associated with reservoir compaction and overburden subsidence[R].SPE 20953, 1990.
|
| [5] |
ROUFFIGNAC E P, BONDOR P L, KARANIKAS J M, et al.Subsidence and well failure in the South Belridge Diatomite field[R].SPE 29626, 1995.
|
| [6] |
HILBERT L B, GWINN R L, MORONEY T A, et al.Field-scale and wellbore modeling of compaction-induced casing failures[R].SPE 56863, 1999.
|
| [7] |
LI X, MITCHUM F L, BRUNO M, et al.Compaction, subsidence, and associated casing damage and well failure assessment for the Gulf of Mexico Shelf Matagorda Island 623 field[R].SPE 84553, 2003.
|
| [8] |
Bruno M S. Geomechanical analysis and decision analysis for mitigating compaction related casing damage[R].SPE 71695, 2001.
|
| [9] |
PENG S, FU J, ZHANG J. Borehole casing failure analysis in unconsolidated formations:a case study[J]. Journal of Petroleum Science & Engineering, 2007, 59(3/4): 226-238. |
| [10] |
DUSSEAULT M B, BRUNO M S, BARRERA J. Casing shear: causes, cases, cures[R].SPE 48864, 1998.
|
| [11] |
GUO Y G, BLANFORD M, CANDELLA J. Evaluating the risk of casing failure caused by high-density perforation: a 3D finite-element-method study of compaction-induced casing deformation in a deepwater reservoir, Gulf of Mexico[R].SPE 170618, 2015.
|
| [12] |
FURUI K, FUH G F, MORITA N. Casing and screen-failure analysis in highly compacting sandstone fields[R].SPE 146231, 2011.
|
| [13] |
CLEGG J D. Casing failure study-cedar creek anticline[J]. Journal of Petroleum Technology, 1971, 23(6). |
| [14] |
MORITA N, MCLEOD H. Oriented perforation to prevent casing collapse for highly inclined wells[R].SPE 28556, 1995.
|
| [15] |
WU J, GONZALEZ M E, HOSN N A. Steam-injection casing design[R].SPE 93833, 2005.
|
| [16] |
PATTILLO P D, KRISTIANSEN T G. Analysis of horizontal casing integrity in the valhall field[R].SPE 78204, 2002.
|
| [17] |
HAIR C C, SCHWIND B E. Evaluation and design optimization of perforated casing[R].OTC 7345, 1993. http://www.emeraldinsight.com/servlet/linkout?suffix=b31&dbid=16&doi=10.1108%2F02621710710740110&key=10.1287%2Finte.13.2.87
|
| [18] |
CERNOCKY E P, SCHOLIBO F C. Approach to casing design for service in compacting reservoirs[R].SPE 30522, 1995.
|
| [19] |
MORITA N, KASAHARA Y, ITO Y, et al. Collapse resistance of tubular strings under geotectonic load[R].SPE 95691, 2005.
|
| [20] |
FUH G, MORITA N, FURUI K. Modeling analysis of sand-screen collapse resistance under geotectonic load[R].SPE 124388, 2009.
|
| [21] |
GUO Y, LAST N, BLANFORD M. Simple calculation of compaction-induced casing deformation adjacent to reservoir boundaries[R].SPE 189694, 2018.
|


