2. 中国石油大学(北京)海洋工程研究院
2. Offshore Engineering Research Institute, China University of Petroleum(Beijing
0 引言
水下生产系统技术已经发展了半个世纪,国外的Shell、Total和Chevron等油田作业者对水下生产系统从设计到安装都有很多成功案例和工程经验,最大应用水深接近3 000 m[1]。但因影响水下生产系统布局的因素众多,其布局方法仍然以工程经验为主对水下生产系统布局形式进行筛选。目前,相关研究人员开始利用数学模型进行深水开发中的技术研究,多应用于浮式平台开发过程中基建成本、钻井成本和操作成本的估算[2-3]。而国内中海油、中石油、中石化、石油大学、上海交通大学以及哈尔滨工程大学等也开始进行深水油气田相关技术的研究,组织核心科研力量对深水浮式结构物和水下生产系统的相关设备与技术进行科研攻关,但对于水下生产系统布局方面的研究,也局限于借助国外公司的设计经验,通过对水下生产设施调试、安装工作量的统计对比,进行水下生产系统布局方案的优选,最大应用水深以1 480 m的荔湾3-1气田为代表[4-6]。
目前,典型的布局形式主要有单井回接、菊花链式回接、基盘管汇和丛式管汇等4种形式[7],尚未有一种成熟的方法,将管汇连接布局建立成有效的数学模型,并通过数学方法进行筛选,建立满足各种条件需求的管汇连接布局方式。笔者通过研究多目标模糊优化的方法将油气田的管汇连接布局数据化,进行必要的人工分析,得到油气田井口分布、区块分划和距离测量等数据,并将数据在MATLAB中进行处理,最终得到管汇布置的必要数据。研究结果对油气田开发中管汇优化布置的科学性有一定的帮助。
1 多目标优化设计在深水、超深水油气田开发中,海工模式优选决策系统的研究成果和应用很少,缺乏系统性和可靠性。对于油田开发的全生命周期,所受的影响因素众多,设备选择困难大,而且有部分因素之间耦合,综合分析众多因素影响规律,要想得出一个最优的开发模式,使得造价最低、可靠性最高难度比较大。而多目标模糊优化的数学模型能很好地解决这方面的难题,具体表现在设计变量的模糊性、约束条件的模糊性以及目标函数的模糊性等,在工程设计应用中非常有效。
1.1 多目标模糊优化的数学模型普通多目标模糊优化问题的目标函数是确定的,但其约束模糊,其数学模型为[8]:
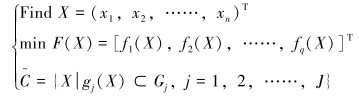
|
(1) |
式中:X为模糊变量集合,F(X)为应取极小化的目标函数集合,gj(X)为关于模糊变量的约束条件集合,Gj表示gj(X)所允许的范围,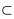
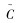
由于模糊变量存在一定的变化范围,而模糊目标函数由模糊变量构成,则模糊目标集中的各个元素也在一定的区间变化,形成了一个模糊目标去极小化的集合F。为了构造模糊目标fk的隶属函数,需要先确定各个单目标的上下边界[9]。在各单目标约束最宽松的情况下,其最小值可以用式(2)求得:
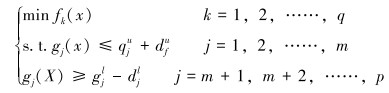
|
(2) |
之后用简单的单目标普通解法求出解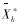
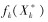
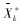
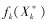
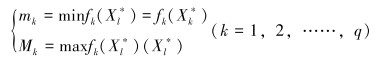
|
(3) |
目标函数的隶属函数与模糊变量的隶属函数一样,都需要根据实际情况选择函数类型,但一般情况下,选择线性函数。同理,其隶属函数为:
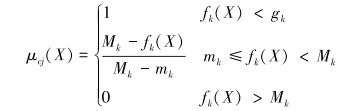
|
(4) |
式中:k=1,2,……,q。
1.3 多目标模糊优化的最优解得到模糊变量的隶属函数和模糊目标的隶属函数后,还需要通过模糊判决法对隶属函数进行处理。模糊判决法也就是对模糊目标集F和模糊约束集C的模糊判决集D构造一个隶属函数μD(X),以求出最优点X*,使最优判决为:
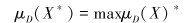
|
(5) |
根据工程中不同的决策方法和决策背景,模糊判决集D的隶属函数μD(x)的建立方法也不尽相同,可分为对称模型、加权型模型、几何平均模型和非对称模型等[10]。采用对称模型,现详细说明对称模型的解题思路。
对称模型即所优化的目标和优化所要满足的限制条件对优化结果的要求相同,则模糊判决集由模糊目标集F和模糊约束集C的交集得出,即:
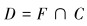
|
(6) |
由于在多目标模糊优化问题中,
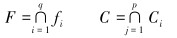
|
(7) |
则隶属函数为:
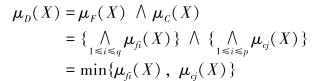
|
(8) |
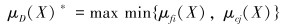
|
(9) |
这种在各个最小值中取最大值的方法也可以叫做最大最小法[11]。
即可将式(1)转化为如下的单目标普通优化:
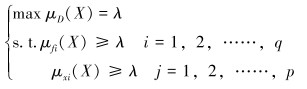
|
(10) |
式中:0≤λ≤1。
将式(10)中的μfi(X)转化为μF(X),即可得到单目标普通优化的方程。该类保守取小型判决反映了使各分目标和各约束中最差分量得到改善的谨慎思想,其结果仅使最差分量极大化,而其余分量在一定范围内变化并不直接影响结果,从而丢掉不少信息[12]。
2 管汇连接多目标优化设计 2.1 管汇连接方案分析由于丛式管汇布局方式工作弹性大,适应性强,安装难度适中,且可以实现分压输送,适用于大多数的深海油气田开发,所以以丛式管汇布局方式进行管汇连接的优化设计。
在设计管汇连接方案中,第一个步骤就是根据水下油气田的井口分布进行分析,确定选用的丛式管汇的工艺流程。在选择丛式管汇工艺流程的时候,应该根据水下一定范围之内的井口数、井位分布、水深、是否需要有清管回路、管线分配和油气田开发的实际需要等一系列因素进行管汇的优化布局设计。
2.2 管汇连接优化目标选定针对上文提出的要求,现将丛式管汇的数量、回路数、丛式管汇的井槽数、输油管道的总长度、跨接管的数量和长度、PLET和PLEM的数量设定为模糊变量;将管汇布局的建设费用和管道的总长度作为优化的两个目标,则有:
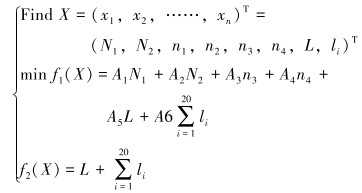
|
(11) |
式中:N1为丛式管汇数量,N2为回路数量,n1为跨接管数,n2为丛式管汇井槽数,n3为PLET数,n4为PLEM数,L为输油管长度,li为跨接管长度,A1为丛式管汇造价,A2为清管费用,A3为PLET造价,A4为PLEM造价,A5为输油管造价,A6为跨接管造价。
2.3 多目标优化中约束条件选定现选定多目标优化的约束条件。选定跨接管长度约束为g1(x),管汇上的预留接口数为g2(x),管汇的质量约束为g3(x),输油管的长度约束为g4(x),并采用分类计算的方法来分层计算。
多目标优化的约束方程如下所示。
跨接管长度约束为:
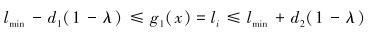
|
(12) |
管汇上预留接口约束为:
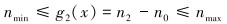
|
(13) |
式中:n0为该区域的井口数,根据实际情况作为已知条件输入。
管汇质量约束为:
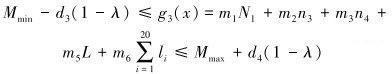
|
(14) |
其中,各部分的质量作为输入的已知条件。
输油管长度约束为:
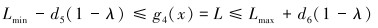
|
(15) |
式(12)~式(15)中的d为各约束的容差,λ为水平截集系数,根据实际工程要求决定。
2.4 管汇连接多目标优化方程根据2.2和2.3节中的目标函数方程和约束条件方程,结合多目标模糊优化的方程要求,可以得到管汇连接的多目标优化方程为:

|
(16) |
式(16)中的一些参数,诸如单个跨接管长度,管汇中心所在的位置坐标,输油管道长度,注水管道长度等变量以及工程造价、管道总长度这两个模糊目标都需要后面程序进行运算得出。
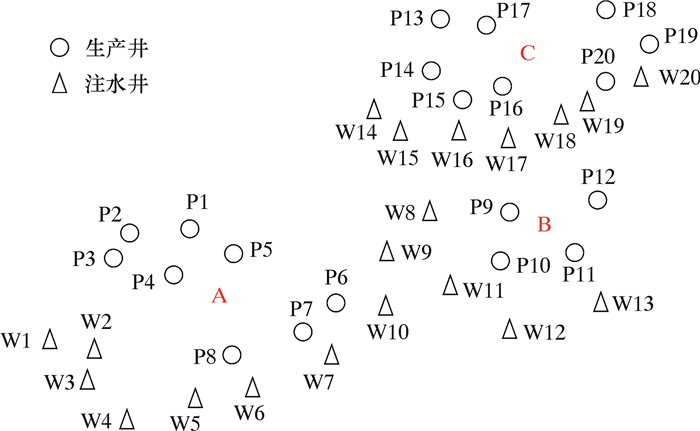
3 案例分析 3.1 有关设计参数的确定下面结合实例(见图 1)来具体分析如何用多目标模糊优化来选定管汇的使用数量、管汇的井槽数、管汇所连接的管道长度、回路数量、跨接管长度和数量以及PLET数量等参数,并说明怎样通过选择的参数找出最优的管汇连接方案。
|
| 图 1 西非E油气田分布图 Fig.1 Distribution map of E oil and gas field in West Africa |
丁非E油气田共有20口生产井和20口注水井,井网明显分为南部(A)、中部(B)和北部(C)3区,A和C区分别有8口生产井和7口注水井,B区包括4口生产井和6口注水井。A区和C区各自的8口生产井又可分别划分为两个明显区域,即A区P1~P5和P6~P8井口相对比较集中,C区P13~P17和P18~P20井口相对比较集中[13],选择丛式管汇的布局形式。考虑到安装的可行性和A、C区都存在可将该区域划分成两部分的分布特点,则丛式管汇的数量可定为3、4、5个。依据E油气田的基础数据,在设计管汇布局方案时应该考虑丛式管汇的数量、连接形式、清管回路、跨接管长度和数量、PLET数、PLEM数以及连接调试的工程量等问题。
现根据各部分加工钢材的价格和加工成本的实际情况,取值如下:丛式管汇的平均价格1 800万元,清管回路的成本造价200万元/条,PLET的造价为400万元/个,PLEM的造价为1 000万元,输油管道的造价为0.18万元/m,跨接管的造价为0.136万元/m,跨接管长度取50~150 m,丛式管汇的平均质量取250 t,PLET的质量取60 t,PLEM的质量取180 t,输油管道的质量取0.085 t/m,跨接管的质量取0.065 t/m,λ取1。
当管汇数选取3个或4个时,A区和C区离区域中心较远的3口油井就需要使用跨接管加PLET以及分支管进行连接。由于PLET的费用较高,且分支管的铺设难度大、成本高,故只有在选用5个管汇的时候,才能找到最佳的布局方案,所以在后续的计算中,重点针对使用5个管汇时的布局方式进行分析。在使用5个管汇的情况下,为了工程标准统一,管汇中心统一选择6井槽。
3.2 寻求全域最优解根据上述情况,用MATLAB编写了寻找管汇坐标点函数,寻找最优路径函数,计算输油管和注水管长度函数,以及计算跨接管长度函数等必需的函数,这些函数都以图论的方法为基础[14-15]。输入平台O点的坐标和A、B、C三个区中每个井口的坐标,通过将丛式管汇的位置到井口距离计算每一个跨接管的长度,应用程序中的迭代方法计算出每一种可能的情况。经过添加约束条件,筛选出符合要求的丛式管汇的连接方式和管道的造价,具体情况见表 1和表 2。再通过后续的数据处理和优化选择,将最优方案找出来,得到最终结果。
| 方案 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 连接方式 | 6-1_6-2_6-3_6-4_6-5 | 6-1-2_6-3_6-4_6-5 | 6-4-5_6-1_6-2_6-3 | 6-1-2-3_6-4_ 6-5 | 6-3-2-1_6-4_ 6-5 | 6-4-5-3_6-1_ 6-2 | 6-3-4-5_6-1_ 6-2 | 6-3-5-4_6-1_ 6-2 | 6-1-2-3-4-5 | 6-3-2-1-4-5 | 6-3-1-2-4-5 | 6-1-2-3-5-4 | 6-3-2-1-5-4 | 6-3-1-2-5-4 | 6-4-5_6-1- 2-3 | 6-3-4-5_6-1-2 | 6-3-5-4-1-2 | 6-4-5-3-2-1 | 6-3-4-5-2-1 | 6-3-5-4-2-1 |
| 注:表中数字“6”代表平台,“1”代表P1~P5所在范围的中心,“2”代表P6~P8所在范围的中心,“3”代表P9~P12所在范围的中心,“4”代表P13~P17所在范围的中心,“5”代表P18-P20所在范围的中心。“-”所连接的元素是顺次相连的,而“_”代表两侧分别独立形成一条回路。如6-1_6-2_6-3_6-4_6-5代表平台分别与5个区域相连,形成5条回路;6-1-2-3-4-5代表平台与5个区顺次相连,形成一条回路。 | ||||||||||||||||||||
| 方案 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 造价/万元 | 2 437 | 2 044 | 2 069 | 1 678 | 1 729 | 1 703 | 1 765 | 1 810 | 1 033 | 1 195 | 1 233 | 1 070 | 1 279 | 1 300 | 1 263 | 1 097 | 1 213 | 1 028 | 1 218 | 1 185 |
值得注意的是,本模型中管汇的最优位置还只是理想情况下的最优值。因深水油气田的高风险、高投入和高回报的特点,最终的最优布局方案的选取,仍然需要结合目标深水油气田的油藏数据、油公司的实际情况,以及风险评估等综合考虑。
3.3 优化结果分析 3.3.1 初步人工筛选当每一个管汇单独形成一条回路时,虽然可以保证清管回路的工作质量,而且能减少PLET和分支管的使用,但是其清管费用十分高昂,最终导致成本过高,故不予采用。而5个管汇全部串接在一起,形成一条回路的情况下,虽然管道长度可以保证最短,但需要大量的分支管和PLET,铺设难度极大,且由于管线过长,可能导致控制方面的问题,而且在清管时还会导致清管回路无法完成工作的情况,故5个管汇串接在一起的情况也不予采用。经过人工筛选得出:方案2~方案8,以及方案15、方案16这9个方案可供选择。
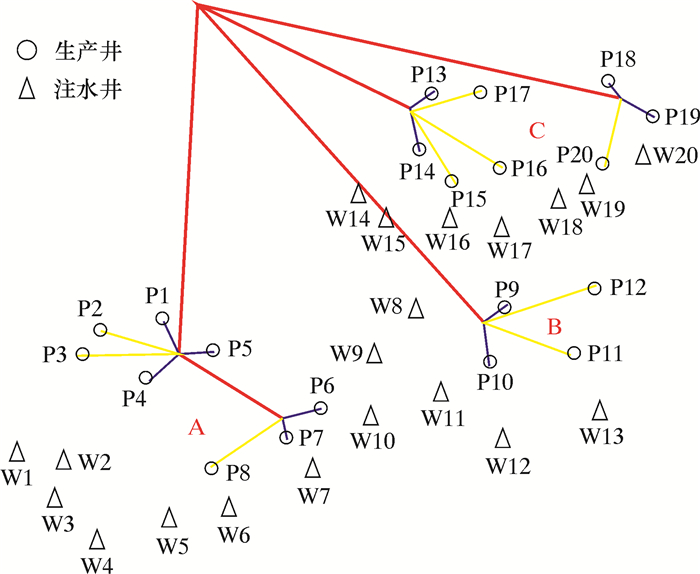
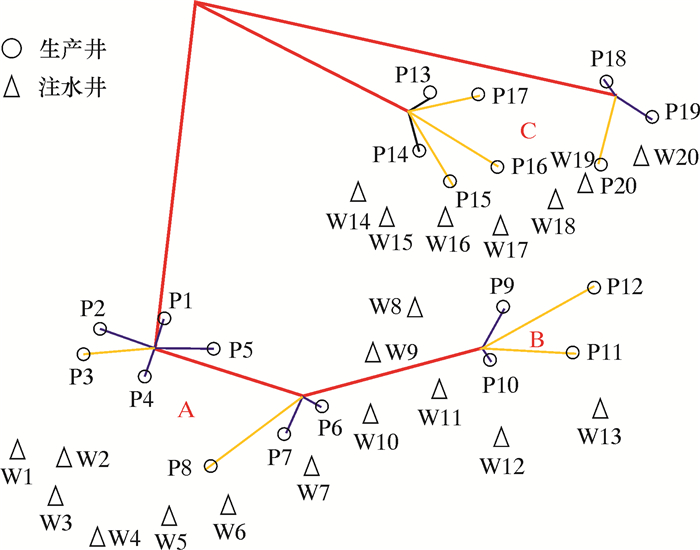
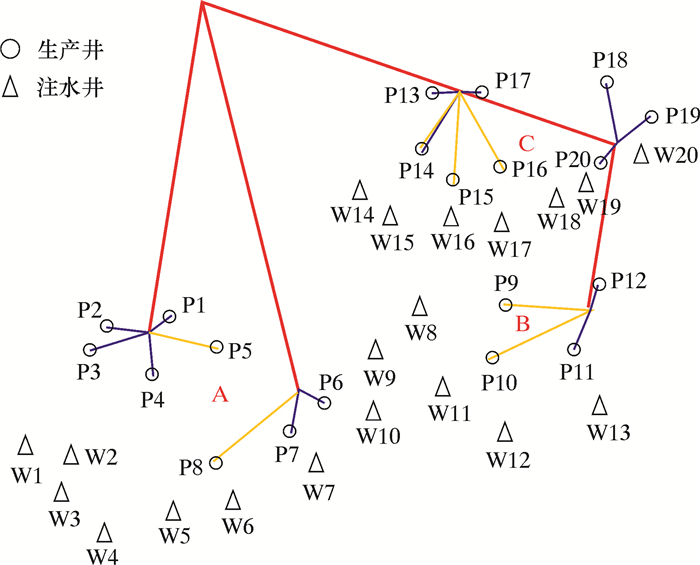
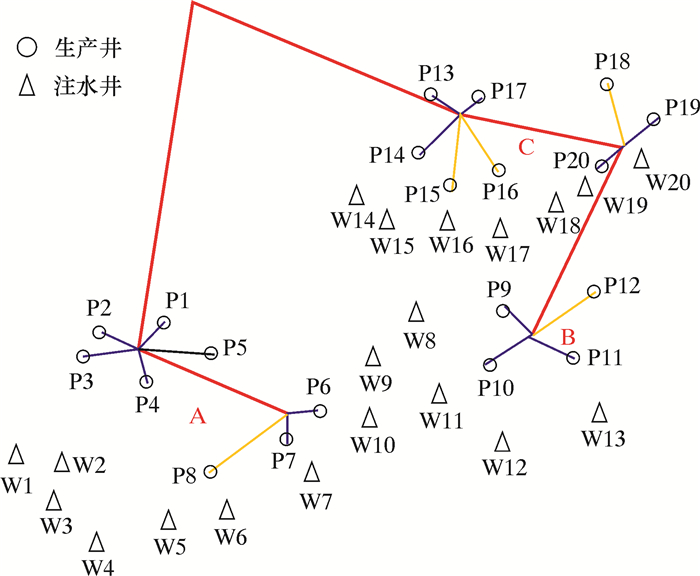
虽然方案2和方案3均为使用4条回路的情况,但是由程序的运行结果可知,方案2的管道总长度和工程造价明显低于方案3,且二者性能相似,因此在使用4个回路的情况中,优选方案2;方案4到方案8都是使用3条回路时的情况,由于平台的位置距离3号管汇中心较远,以“6-3-x”起始的均相对较差,所以在3条回路的情况下,方案4和方案6优于其他方案;方案15和方案16均为使用2条回路的情况,而由程序运行结果可知,方案16的管道长度和工程造价明显低于方案15,在选择时方案16更优,所以选择方案16为优选方案。经过整理,将相同回路中更优秀的情况作为备用方案,各优选方案的管汇连接示意图见图 2~图 5,其中红色线条代表输油管道,蓝色线条代表跨接管,黄色线条代表使用了PLET的管道。
|
| 图 2 方案2 Fig.2 Scheme 2 |
|
| 图 3 方案4 Fig.3 Scheme 4 |
|
| 图 4 方案6 Fig.4 Scheme 6 |
|
| 图 5 方案16 Fig.5 Scheme 16 |
3.3.2 方案验证和改进
现在的方案中各个区域PLET的使用情况见表 3。由于PLET的造价远远高于管道的造价,所以可以通过适当的增大管道的长度来减小PLET的使用数量,以达到成本的降低。根据油田实际情况可知,区域1、2、3的PLET需求量最少为1,区域4、5可以不使用PLET,在上述优选方案的基础上,再对从式井管汇中心位置做优化,使各个区域的PLET使用组数降低到最少,成本计算公式如下。
| 方案 | 区域1 | 区域2 | 区域3 | 区域4 | 区域5 |
| 方案2 | 2 | 1 | 2 | 3 | 1 |
| 方案4 | 1 | 1 | 2 | 3 | 1 |
| 方案6 | 1 | 1 | 2 | 3 | 0 |
| 方案16 | 1 | 1 | 1 | 2 | 1 |
改进前成本:P1=管道及清管回路的成本+管汇数量*管汇价格+PLET组数*PLET价格。
改进后成本:P1=管道及清管回路的成本+管汇数量*管汇价格+PLET组数*PLET价格。
计算结果见表 4。
| 方案 | 方案2 | 方案4 | 方案6 | 方案16 |
| 改进前/万元 | 15 444 | 14 478 | 12 811 | 11 928 |
| 改进后/万元 | 13 506 | 12 863 | 12 811 | 11 928 |
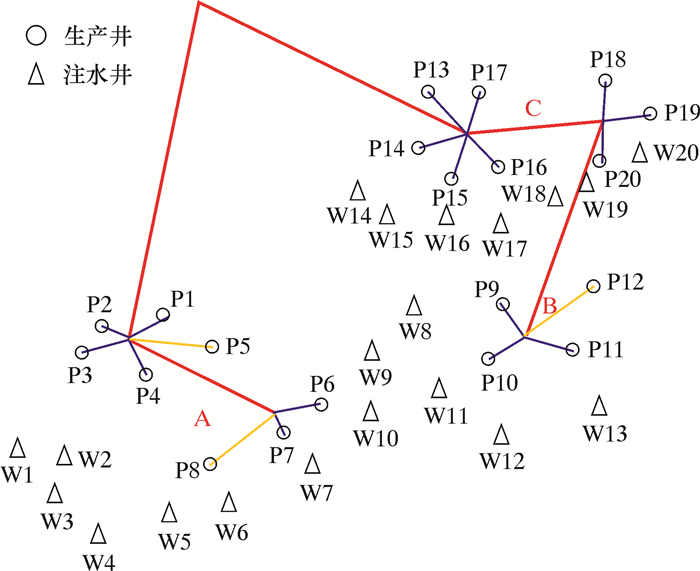
显然,方案16的造价成本最低,方案6其次,之后为方案4,成本最高的是方案2。因此选用改进的方案16作为最优方案,其管汇中心位置改进后的连接情况见图 6,这样处理既保证了输油管线长度的最短,又减少了PLET的使用数量,大大缩小了成本价格,这也与该油气田的实际管汇连接方案不谋而合。
|
| 图 6 改进后的方案16 Fig.6 Improved scheme 16 |
4 结束语
通过对管汇连接设计优化方案的研究,发现多目标模糊优化在管汇连接的工程设计中具有较高的可行性,以西非深水E油田为目标油田,通过设定工程造价和管道总长度为优化目标,以管汇数量、回路数量、输油管线长度等参数为优化函数变量,并通过MATLAB软件进行程序编写以及对程序输出数据进行分析,获得了管汇布局的优化连接方案,极大地减小了人工计算量,提升了管汇连接设计方案的性能,解决了目前尚未通过精确的理论计算寻找管汇连接的最优化设计方案的问题,同时为今后进行管汇布局研究提供了一种可借鉴的方法。
| [1] |
李清平. 我国海洋深水油气开发面临的挑战[J]. 中国海上油气, 2006, 18(2): 130-133. LI Q P. The situation and chanllenges for deepwater oil and gas exploration and exploitation in China[J]. China Offshore Oil and Gas, 2006, 18(2): 130-133. DOI:10.3969/j.issn.1673-1506.2006.02.013 |
| [2] |
JABLONOWSKI C J. Empirical cost models for TLPs and spars[R]. SPE 115483-MS, 2008.
|
| [3] |
KAISER M J, PVLSIPHER A G. Generalized functional models for drilling cost estimation[R]. SPE 98401-PA, 2007.
|
| [4] |
SCOTT S L, DEVEGOWDA D, MARTIN A M. Assessment of subsea production & well systems[C]//The U.S.Department of Interior-Minerals Management Service(MMS).Technology Assessment & Research (TA & R) Program, Texas: [s. n.], 2004.
|
| [5] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会.石油天然气工业水下生产系统的设计与操作: 第6部分水下生产控制系统: GB/T 21412.6-2009[S].北京: 中国标准出版社, 2009. General Administration of Quality Supervision, Inspection and Quarantineof the People's Republic of China. Design and operation of an underwater production system for the petroleum and natural gas industry-part 6: Underwater production control system: GB/T 21412.6-2009[S]. Beijing: Standards Press of China, 2009. |
| [6] |
王莹莹, 段梦兰, 冯玮, 等. 深水管汇安装方法及其在南海荔湾3-1气田中应用研究[J]. 海洋工程, 2011, 29(3): 23-30. WANG Y Y, DUAN M L, FENG W, et al. Investigation on installation methods of deepwater manifolds and their applications to LW3-1 gas field in South China Sea[J]. The Ocean Endineering, 2011, 29(3): 23-30. DOI:10.3969/j.issn.1005-9865.2011.03.003 |
| [7] |
程兵, 李清平, 黄冬云, 等. 水下生产系统管汇布置研究[J]. 石油机械, 2015, 43(3): 60-63. CHENG B, LI Q P, HUANG D Y, et al. Configuration of manifolds in underwater production system[J]. China Petroleum Machinery, 2015, 43(3): 60-63. |
| [8] |
张晓丽, 杨建强, 常春影, 等. 多目标模糊优化方法及其在工程设计中应用[J]. 大连理工大学学报, 2005, 45(3): 374-378. ZHANG X L, YANG J Q, CHANG C Y, et al. Multi-objective fuzzy optimization method and its practical application to engineering design[J]. Journal of Dalian University of Technology, 2005, 45(3): 374-378. DOI:10.3321/j.issn:1000-8608.2005.03.014 |
| [9] |
YAGER R R. Multiple objective decision-making using fuzzy sets[J]. International Journal of Man-Machine Studies, 1977, 9(4): 375-382. DOI:10.1016/S0020-7373(77)80008-4 |
| [10] |
MIRJALILI S, SAREMI S, MIRJALILI S M, et al. Multi-objective grey wolf optimizer:a novel algorithm for multi-criterion optimization[J]. Expert Systems with Applications, 2016, 47: 106-119. DOI:10.1016/j.eswa.2015.10.039 |
| [11] |
郭军, 肖熙, 朱静. 海洋工程结构的多目标模糊优化设计[J]. 海洋工程, 1994(4): 1-7. GUO J, XIAO X, ZHU J. Multi-objective fuzzy optimization design of marine engineering structure[J]. Ocean Engineering, 1994(4): 1-7. |
| [12] |
公茂果, 焦李成, 杨咚咚. 进化多目标优化算法研究[J]. 软件学报, 2009, 20(2): 271-289. GONG M G, JIAO L C, YANG D D. Study on evolutionary multi-objective optimization algorithm[J]. Journal of Software, 2009, 20(2): 271-289. |
| [13] |
王莹莹, 王德国, 段梦兰, 等. 水下生产系统典型布局形式的适应性研究[J]. 石油机械, 2012, 40(4): 58-63. WANG Y Y, WANG D G, DUAN M L, et al. Study on the adaptability of typical layout of underwater production system[J]. China Petroleum Machinery, 2012, 40(4): 58-63. |
| [14] |
TRUCK I. Comparison and links between two 2-tuple linguistic models for decision making[M]. Amsterdam: Elsevier Science Publishers B. V., 2015.
|
| [15] |
方富贵. 图论的算法和应用研究[J]. 计算机与数字工程, 2012, 40(2): 115-117. FANG F G. Algorithm and application of graph theory[J]. Computer & Digital Engineering, 2012, 40(2): 115-117. DOI:10.3969/j.issn.1672-9722.2012.02.038 |


