2. 中国石油大学(华东)机电工程学院
2. College of Mechanical and Electronic Engineering, China University of Petroleum(Huadong
0 引言
水下生产系统控制系统的主要类型有液压控制系统、电液复合控制系统和全电控制系统等3种[1]。研究较成熟且应用较多的是全液控制系统[2]和电液复合控制系统[3]。液压动力单元的作用是为控制系统提供稳定清洁的液压油[4]。由于水下采油树上的执行机构分为高压和低压两种[5],所以液压动力单元能够提供高压和低压两种压力的液压油。
目前,对于水下生产系统的故障诊断研究并不多,且主要集中在系统的跨接管上。胡飚等[6]通过仿真,对跨接管在不同水流速度下的振动响应做了定量研究。余建星等[7]通过仿真对跨接管热应力的分布以及影响因素进行了系统研究。马增骥等[8]对端部相对位移载荷作用下跨接管的承载极限和失效形式进行了研究。赖文龙等[9]对跨接管在地震作用下的动力响应进行了研究。故障诊断精度以及多故障并发的诊断是故障诊断领域的关键问题[10-13]。融合多源信息能够有效提高故障诊断的精度,并可进行多发并发故障的诊断[14]。贝叶斯网络因其独特的优势能够有效融合多源信息进行推理分析[15]。
由于水下生产系统具有工作环境复杂,维修成本高昂,一旦发生故障则后果严重等特点,所以开展水下生产系统故障诊断方法研究有助于降低生产风险,提高企业生产效率。笔者根据API标准要求,设计了一套液压动力单元原理图,并在此基础上,开展了融合多源信息的液压动力单元贝叶斯网络故障诊断方法研究,以期为下一步水下生产系统的故障诊断奠定基础。
1 液压动力单元 1.1 液压系统工作原理图 1所示为液压动力单元的液压系统,主要元件包含:油箱1,闸阀2.1、2.2、7.1、7.2,过滤器3.1、3.2,液压泵4.1、4.2,溢流阀5.1、5.2、11.1~11.4、15.1、15.2,单向阀6.1、6.2,压力传感器8.1~8.4、17.1、17.2、21.1、21.2,压力表 9.1、9.2、16.1、16.2、20.1、20.2,蓄能器组10.1~10.4,隔离阀组12.1~12.2,滤油器组13.1、13.2,减压阀14.1、14.2,先导换向阀18.1、18.2,液压换向阀19.1、19.2,接头22.1、22.2。整个液压系统包含高压和低压两条独立的回路。高压回路提供的高压油为井下安全阀提供动力,而低压回路则是为生产阀和化学药剂注入阀等提供动力。两部分结构基本一致,主要区别在于元件的耐压参数不同。
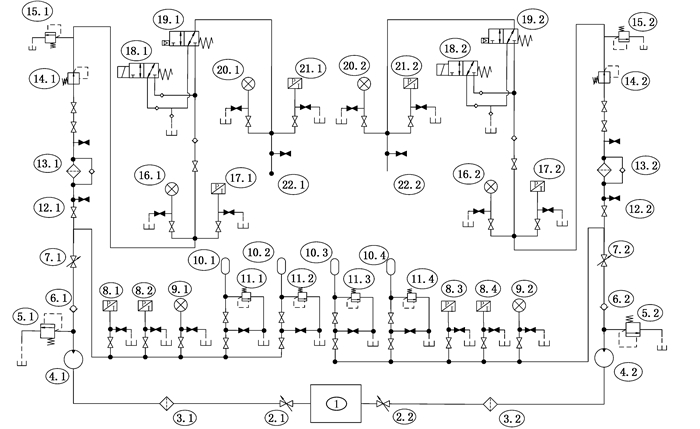
|
| 图 1 液压动力单元液压系统工作原理图 Fig.1 Working principle diagram of hydraulic system of the hydraulic power unit |
以高压回路为例说明系统的工作过程。当需要系统提供压力时,泵4.1经由闸阀2.1和滤油器3.1从油箱1中抽取液压油,并将液压油加压。蓄能器组储存泵回路提供的高压液,待系统需要补油时,蓄能器组泄油供能。经过泵加压的油随后进入减压回路,经过滤油器13.1过滤后,进入减压阀14.1,减压阀出口油液压力即为执行机构所需的工作油压,随后液压油经过管线被传送至执行机构完成执行动作。压力传感器的作用是监测系统的压力,当系统压力低于要求压力时,控制系统将重新启动油泵为系统加压,反之,将关停油泵。
1.2 故障分析液压系统故障与监测传感器数据之间的关系如表 1所示,共8种故障15处监测传感器。表中每列代表对应故障发生时,各个传感器监测数据的变化趋势。
| 参数 | 油泵内泄漏 | 油泵进油 口漏气 |
减压阀故障 | 先导换向 阀无动作 |
换向阀 误动作 |
减压阀前 管线泄漏 |
蓄能器前 管线泄漏 |
换向阀前 管线泄漏 |
| 泵前压力 | 正常 | 偏大 | 正常 | 正常 | 正常 | 正常 | 正常 | 正常 |
| 泵前流量 | 正常 | 偏小 | 正常 | 正常 | 正常 | 正常 | 正常 | 正常 |
| 泵后压力 | 正常 | 偏小 | 正常 | 正常 | 正常 | 正常 | 正常 | 正常 |
| 泵后流量 | 偏小 | 偏小 | 正常 | 正常 | 正常 | 正常 | 正常 | 正常 |
| 蓄能器组前压力 | 正常 | 偏小 | 正常 | 正常 | 正常 | 偏小 | 偏小 | 正常 |
| 减压阀前压力 | 正常 | 偏小 | 正常 | 正常 | 正常 | 偏小 | 正常 | 正常 |
| 减压阀前流量 | 偏小 | 偏小 | 正常 | 正常 | 正常 | 偏小 | 正常 | 正常 |
| 减压阀后压力 | 正常 | 偏小 | 偏大 | 正常 | 正常 | 偏小 | 正常 | 正常 |
| 减压阀后流量 | 偏小 | 偏小 | 正常 | 正常 | 正常 | 偏小 | 正常 | 正常 |
| 先导阀前压力 | 正常 | 偏小 | 偏大 | 正常 | 正常 | 偏小 | 正常 | 偏小 |
| 先导阀前流量 | 偏小 | 偏小 | 正常 | 正常 | 正常 | 偏小 | 正常 | 偏小 |
| 先导阀后压力 | 正常 | 偏小 | 偏大 | 偏小 | 正常 | 偏小 | 正常 | 偏小 |
| 先导阀后流量 | 偏小 | 偏小 | 正常 | 偏小 | 正常 | 偏小 | 正常 | 偏小 |
| 换向阀后压力 | 正常 | 偏小 | 偏大 | 偏小 | 偏大 | 偏小 | 正常 | 偏小 |
| 换向阀后流量 | 偏小 | 偏小 | 正常 | 偏小 | 偏大 | 偏小 | 正常 | 偏小 |
以减压阀故障为例说明各个相关参数的变化情况。当减压阀出现故障时,经过其调节的油液压力会大于目标值,从而导致其后元件压力监测值均大于正常值。由于供油回路与减压回路之间存在单向阀,所以减压阀故障造成的压力波动不会对单向阀之前的回路造成影响,不会影响供油回路的状态监测值。
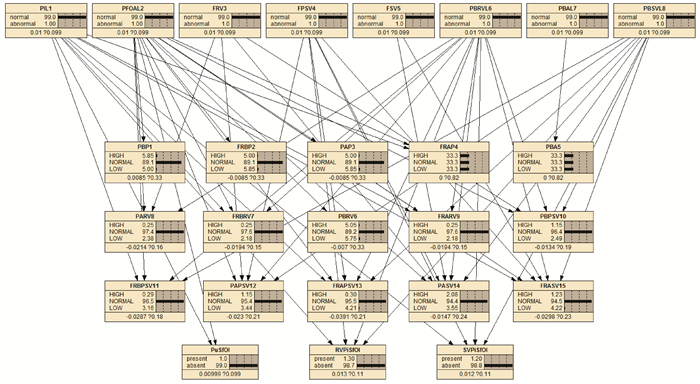
2 基于贝叶斯网络的液压动力单元故障诊断方法 2.1 液压动力单元贝叶斯故障诊断网络结构建模建立液压动力单元的贝叶斯故障诊断模型结构,如图 2所示。该故障诊断网络有两层:上层是故障层,包含8个故障节点,每个故障节点有normal(正常)和abnormal(异常)两种状态;下层是监测层即故障征兆层,包含15个传感器节点,每个节点有High(高)、Normal(中)和Low(低)3种状态。两层节点之间的依赖关系用带有箭头的弧线表示。弧线的方向由故障层节点指向对应的监测层节点。故障节点以及监测节点的名词释义如表 2所示。
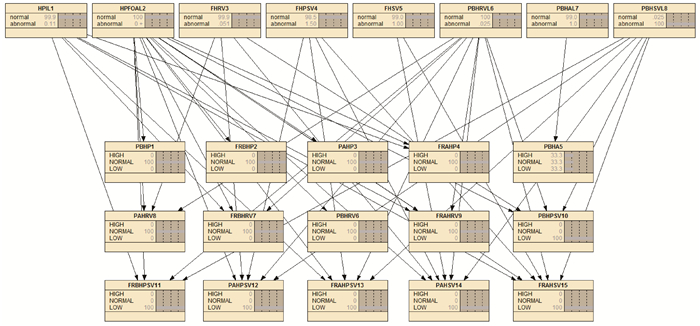
|
| 图 2 液压动力单元故障诊断贝叶斯网络 Fig.2 Bayesian network for hydraulic power unit fault diagnosis |
| 符号 | 含义 |
| PBP(Pressure Before Pump) | 泵前压力 |
| FRBP(Fluid Rate Before Pump) | 泵前流量 |
| PAP(Pressure After Pump) | 泵后压力 |
| FRAP(Fluid Rate After Pump) | 泵后流量 |
| PBRV(Pressure Before Reducing Valve) | 减压阀前压力 |
| FRBRV(Fluid Rate Before Reducing Valve) | 减压阀前流量 |
| PARV(Pressure After Reducing Valve) | 减压阀后压力 |
| FRARV(Fluid Rate After Reducing Valve) | 减压阀后流量 |
| PFOAL(Pump For Oil Air Leak) | 油泵进油口漏气 |
| FPSV(Fault Pilot Selector Valve) | 先导换向阀故障 |
| PBRVL(Pipeline Before Reducing Valve Leak) | 减压阀前管线泄漏 |
| PBSVL(Pipeline Before Selector Valve Leak) | 换向阀前管线泄漏 |
| PBPSV(Pressure Before Pilot Selector Valve) | 先导换向阀前压力 |
| FRBPSV(Fluid Rate Before Pilot Selector Valve) | 先导换向阀前流量 |
| PAPSV(Pressure After Pilot Selector Valve) | 先导换向阀后压力 |
| FRAPSV(Fluid Rate After Pilot Selector Valve) | 先导换向阀后流量 |
| PASV(Pressure After Selector Valve) | 换向阀后压力 |
| FRASV(Fluid Rate After Selector Valve) | 换向阀后流量 |
| PBA(Pressure Before Accumulator) | 蓄能器前压力 |
| PIL(Pump Inside Leak) | 油泵内泄漏 |
| FRV(Fault Reducing Valve) | 减压阀故障 |
| FSV(Fault Selector Valve) | 换向阀故障 |
| PBAL(Pipeline Before Accumulator Leak) | 蓄能器前管线泄漏 |
2.2 液压动力单元贝叶斯故障诊断网络参数建模
应用贝叶斯网络进行故障诊断,需要确定网络中故障节点的先验概率和监测节点条件概率。假定所有故障节点发生的先验概率为1%,即初始状态为正常状态,故障发生于系统运行过程中。在确定监测节点的条件概率时,当监测节点的父节点数量增加时,需要确定的监测节点的条件概率数量会成指数增长[15]。例如,某一监测节点有m个状态,其父节点有n个且每一个父节点具有l种状态,那么在确定这一监测节点的条件概率时就需要确定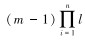
利用Noisy-OR或Noisy-MAX可以减少条件概率的计算量[16],且计算结果满足要求,二者区别在于节点状态的数量。本模型中,监测节点都是三状态的变量,因此采用Noisy-MAX计算监测节点的条件概率。最后将计算结果输入建立的结构模型中就得到了完整的贝叶斯故障诊断网络。
Noisy-MAX是Noisy-OR在非两状态变量领域的一般形式。仍假设有X1,……, Xn共n种可能会造成Y这一结果的发生。但每一种可能Xi不再只有两种状态,其状态被按照代表事件的严重程度进行数字排序,0表示这个变量代表的事件未发生,其余假设与Noisy-OR相同。
假定随机变量X具有dX种状态,则X的所有状态可以被表示为s {0, 1, ……, dX-1}。要使用Noisy-MAX计算节点的条件概率需要用到如下参数。
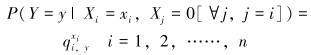
|
(1) |
在得到上述参数后,通过下面的公式便可计算出其余需要的条件概率。
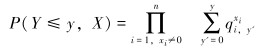
|
(2) |
式中:X代表与Y=y对应的一组X的取值,X=x1, x2,……, xn。
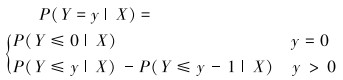
|
(3) |
为了提高贝叶斯网络对两并发故障诊断的精度,引入观测节点,即一些非传感器检测信息。引入的观测节点如表 3所示。
| 节点名称 | 含义 |
| PuSfOl(Pump Surface Has Oil) | 泵表面有油 |
| RVPiSfOl(Reducing Valve Surface Has Oil) | 减压阀管线表面有油 |
| SVPiSfOl(Shift Valve Surface Has Oil) | 换向阀管线表面有油 |
观测节点与故障节点的关系如表 4所示。
| Child node | State | Fault node (present) | ||||
| PIL | PFOAL | FPSV | PBRVL | PBSVL | ||
| PuSfOl | present | 0.9 | 0.1 | — | — | — |
| absent | 0.1 | 0.9 | — | — | — | |
| RVPiSfOl | present | 0.2 | — | 0.1 | 0.9 | 0.1 |
| absent | 0.8 | — | 0.9 | 0.1 | 0.9 | |
| SVPiSfOl | present | 0.1 | — | 0.1 | 0.1 | 0.9 |
| absent | 0.9 | — | 0.9 | 0.9 | 0.1 | |
故障节点和观测节点均为两状态的布尔变量。因此,使用Noisy-OR计算所有观测节点的完整CPT表。修改后的贝叶斯网络诊断模型如图 3所示。
|
| 图 3 加入观测信息的贝叶斯网络 Fig.3 Bayesian network with the observation information |
3 故障诊断结果与分析
表 5为4个故障诊断验证实例,包含单一故障和两并发故障两种情况。单一故障案例Case1中故障PIL发生,Case2中故障PFOAL发生;两故障并发案例Case1中故障PIL和PBRVL同时发生,Case2中故障PIL和PFAOAL同时发生。
| 故障节点 | 单一故障 | 两故障并发 | |||
| Case1 | Case2 | Case1 | Case2 | ||
| PBP | Normal | Higher | Normal | Higher | |
| FRBP | Normal | Lower | Lower | Lower | |
| PAP | Higher | Normal | Normal | Normal | |
| FRAP | Lower | Lower | Lower | Lower | |
| PBRV | Higher | Lower | Lower | Higher | |
| FRBRV | Lower | Lower | Lower | Lower | |
| PARV | Normal | Normal | Lower | Lower | |
| FRARV | Lower | Lower | Lower | Lower | |
| PBPSV | Normal | Lower | Lower | Normal | |
| FRBPSV | Lower | Lower | Lower | Lower | |
| PAPSV | Normal | Normal | Normal | Normal | |
| FRAPSV | Lower | Lower | Lower | Lower | |
| PASV | Normal | Lower | Lower | Lower | |
| FRASV | Lower | Lower | Lower | Lower | |
故障判定准则为:对于某一故障节点,当其后验概率与先验概率之差不小于50%时,则认为该故障节点对应故障发生。
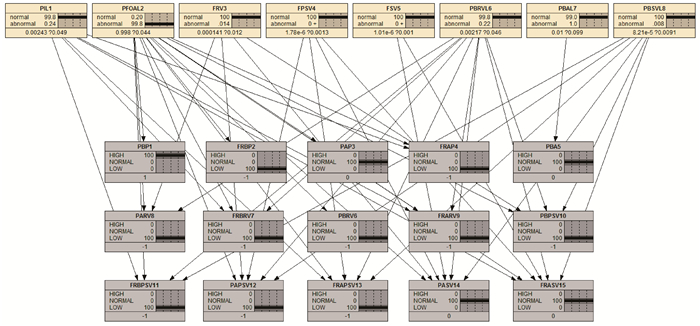
单一故障Case1诊断结果如图 4所示。在单一故障测试案例Case1中,PIL故障发生的后验概率从1%上升至100%,其余故障节点均保持原状,按照故障判别准则可判定只有故障PIL发生,这与实际情况相符。图 5为单一故障Case2诊断结果。由图 5可知,故障PFOAL的后验概率由1%上升至99.8%,满足故障发生的判定条件,且与实际情况相符。因此,该诊断模型对单一故障诊断的精度很高。
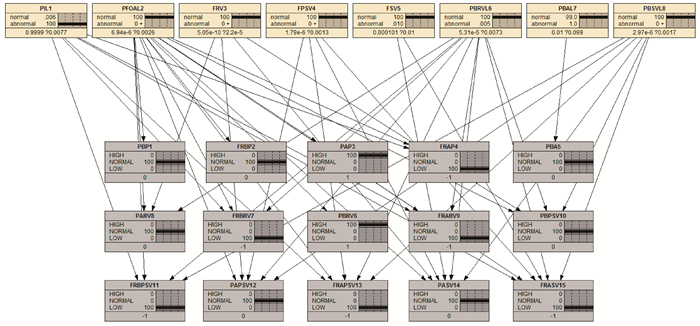
|
| 图 4 单一故障Case1诊断结果 Fig.4 Diagnositic result of Case1 of single fault |
|
| 图 5 单一故障Case2诊断结果 Fig.5 Diagnositic result of Case2 of single fault |
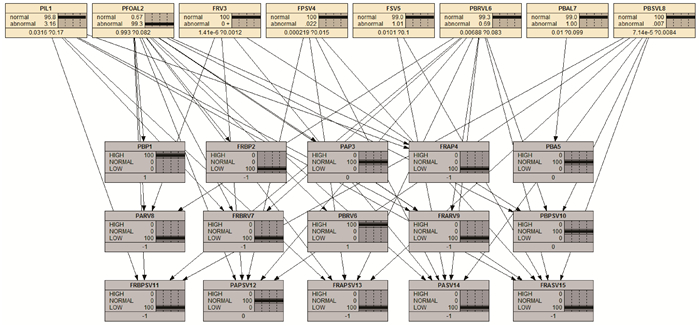
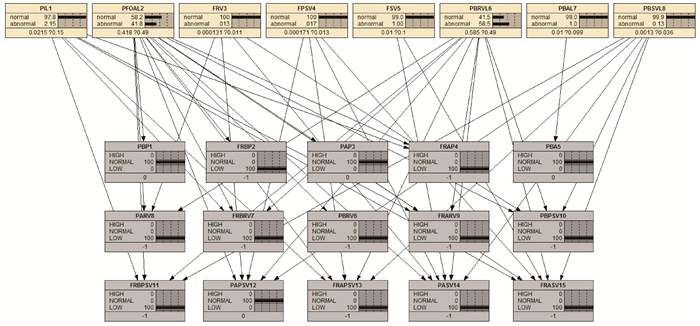
图 6为两故障并发Case1模型诊断结果。由图 6可知,故障PFOAL发生的后验概率由1%上升至99.3%,其余故障节点概率小幅波动。与实际情况相比,模型没能诊断出故障PIL,出现漏诊。图 7为两故障并发Case2模型诊断结果。图 7的验证结果显示,故障PFOAL和PBRVL发生的后验概率分别由1%上升至41.8%和58.5%,这两种故障很有可能发生。但这与实际情况(PIL和PBRVL故障同时发生)不符,出现了误诊。
|
| 图 6 两故障并发Case1模型诊断结果 Fig.6 Diagnositic result of Case1 of two simultaneous faults |
|
| 图 7 两故障并发Case2模型诊断结果 Fig.7 Diagnositic result of Case2 of two simultaneous faults |
对于融合观测节点的贝叶斯网络故障诊断模型,也分为单一故障和两故障并发两种情况进行验证,测试实例如表 6所示。表中仅为观测结点的测试状态,其余节点状态仍沿用表 5中的数据。
| 故障节点 | 单一故障 | 两故障并发 | ||
| PuSfOl | present | absent | present | present |
| RVPiSfOl | absent | - | present | absent |
| SVPiSfOl | absent | - | absent | absent |
验证结果显示,对于单一故障的两个测试案例,修改后的贝叶斯网络延续了之前的诊断精度。
考虑观测节点的贝叶斯故障诊断网络,对于两并发故障的诊断精度有了明显提升。图 8为两故障并发Case1+故障诊断结果。图 8结果显示,故障节点PIL和POFAL的后验概率分别从1%上升至99.7%和98.8%,由此可判定故障PIL和PFOAL同时发生。模型诊断结果与实际情况相符。两故障并发Case2+故障诊断结果如图 9所示。由图 9可知,Case2+诊断结果也与实际故障一致。这表明修改后的模型能够有效进行两并发故障的诊断,解决了漏诊和误诊的问题。

|
| 图 8 两故障并发Case1+故障诊断结果 Fig.8 Diagnositic result of Case1+ of two simultaneous faults |

|
| 图 9 两故障并发Case2+故障诊断结果 Fig.9 Diagnositic result of Case2+ of two simultaneous faults |
两模型对单一故障测试实例Case1诊断结果比较如图 10所示。图 10中,Case1代表未考虑观测信息,Case1+代表考虑观测信息的情况。由图 10可知,两种模型对这个测试实例的诊断结果都很好,故障PIL的后验概率分别为0.99和1.00。测试实例2结果与实例1的结果相仿,由此可知修改后的模型对单一故障的诊断精度略好于未修改的模型。

|
| 图 10 单一故障Case1诊断结果比较 Fig.10 Verification results of Case1 of single fault |
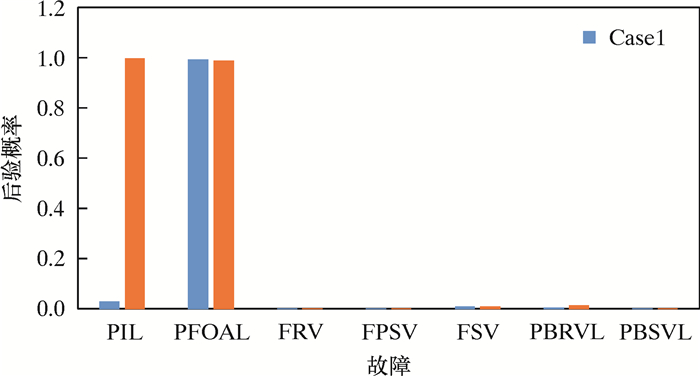
两模型对两故障并发测试实例1的诊断结果比较如图 11所示。图 11中,Case1代表未考虑观测信息,Case1+代表考虑观测信息。Case1中PIL和PFOAL的后验概率分别为0.31和0.99,诊断结果显示只有故障PFOAL被诊断出,即出现了漏诊。在Case1+中,PIL和PFOAL的后验概率分别为0.997和0.999,两种故障都被准确诊断。
|
| 图 11 两故障网络Case1诊断结果比较 Fig.11 Diagnosis results comparison of Case1 of two faults network |
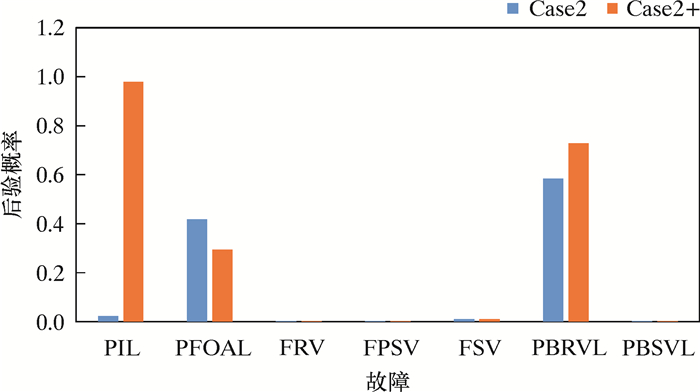
两模型对两故障并发测试实例2的诊断结果如图 12所示。图 12中,Case2代表未代表考虑观测信息,Case2+考虑观测信息。Case2中PFOAL和PBRVL的后验概率分别为0.42和0.58,诊断结果显示故障PFOAL和PBRVL很可能发生,但这与实际情况PIL和PBRVL故障不符,即出现了误诊。在Case2+中,PIL和PBRVL的后验概率分别为0.98和0.73,两种故障都被准确诊断。
|
| 图 12 两故障网络Case2诊断结果比较 Fig.12 Diagnosis results comparison of Case2 of two faults network |
4 结论
为了准确诊断水下生产系统液压动力单元的单一与并发故障,提出一种融合多源信息的贝叶斯网络故障诊断新方法,得到如下结论:
(1) 根据API关于液压动力单元的功能设计要求,设计了一种满足要求的液压动力单元液压系统,该液压系统包含供油模块、调压模块、紧急关断模块、接口模块以及蓄能器模块。
(2) 针对液压动力单元可能出现的单一失效情况,在回路相关元件附近设置15个传感器监测目标元器件的输入输出温度和压力值,并基于此建立液压动力单元的贝叶斯网络故障诊断模型,通过Noisy-Max确定贝叶斯网络节点的概率参数;考虑观测节点作为多失效并发故障诊断的辅助节点,建立考虑观测信息的贝叶斯故障诊断网络,并确定其概率参数。
(3) 诊断结果表明:对单一失效的诊断,观测节点对诊断结果的影响不大,正确率均接近100%;对于两失效同时发生的情况,未考虑观测信息的模型出现了漏诊和误诊的问题,正确率不到50%,而考虑观测信息的模型能够正确诊断出所有两失效并发的情况,正确率达到100%。
| [1] |
FUDGE D, DONOVAN J F. Multiplex control system the heart to the operability of subsea development[R]. AUTOE-V22-023, 1990.
|
| [2] |
ISO. Petroleum and natural gas industries design and operation of subsea production system-Part 6: Subsea production control system: ISO 13628-6: 2006[S]. Geneva: International Organization for Standards, 2006.
|
| [3] |
范亚民. 水下生产控制系统的发展[J]. 石油机械, 2012, 40(7): 45-49. FAN Y M. Development of underwater production control system[J]. China Petroleum Machinery, 2012, 40(7): 45-49. |
| [4] |
张宪阵, 王晓敏, 张凡, 等. 水下生产系统液压动力单元液压系统原理研究[J]. 液压与气动, 2014(10): 33-37. ZHANG X Z, WANG X M, ZHANG F, et al. Hydraulic theory study for hydraulic power unit of subsea production control system[J]. Chinese Hydraulics & Pneumatics, 2014(10): 33-37. DOI:10.11832/j.issn.1000-4858.2014.10.007 |
| [5] |
王鑫, 左信, 马恬然, 等. 水下采油树液压系统高压回油压力分析[J]. 海洋工程装备与技术, 2016, 3(5): 298-304. WANG X, ZUO X, MA T R, et al. Study on the high pressure oil return of subsea christmas tree hydraulic control system[J]. Ocean Engineering Equipment and Technology, 2016, 3(5): 298-304. |
| [6] |
胡飚, 朱宏武, 丁矿, 等. 水下跨接管的外部扰流及振动分析[J]. 石油机械, 2016, 44(4): 42-45. HU B, ZHU H W, DING K, et al. Analysis on exterior circumferential flow and vibration of subsea jumper[J]. China Petroleum Machinery, 2016, 44(4): 42-45. |
| [7] |
余建星, 刘春辉, 何宁, 等. 深水跨接管热应力计算及敏感性分析[J]. 天津理工大学学报, 2015, 31(1): 1-6. YU J X, LIU C H, HE N, et al. Calculation and sensitivity analysis of the thermal stress in a deepwater jumper[J]. Journal of Tianjin University of Technology, 2015, 31(1): 1-6. DOI:10.3969/j.issn.1673-095X.2015.01.001 |
| [8] |
马增骥, 唐文勇, 薛鸿祥. 水下生产系统跨接管结构极限承载能力分析[J]. 海洋工程, 2013, 31(1): 9-15. MA Z J, TANG W Y, XUE H X. Ultimate strength analysis of a jumper in subsea production facility[J]. The Ocean Engineering, 2013, 31(1): 9-15. |
| [9] |
赖文龙, 唐文勇, 薛鸿祥. 水下生产系统跨接管结构在地震作用下动力响应分析[J]. 振动与冲击, 2013, 32(4): 48-53. LAI W L, TANG W Y, YUE H X. Dynamic responses of a jumper in a subsea production facility under earthquake[J]. Journal of Vibration and Shock, 2013, 32(4): 48-53. DOI:10.3969/j.issn.1000-3835.2013.04.010 |
| [10] |
CAI B P, HUANG L, XIE M. Bayesian networks in fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2017(13): 2227-2240. |
| [11] |
张玉龙, 段梦兰, 段礼祥, 等. 基于SAX的往复压缩机气阀故障诊断[J]. 石油机械, 2018, 46(3): 78-83. ZHANG Y L, DUAN M L, DUAN L X, et al. SAX-based fault diagnosis of air valve on reciprocating compressor[J]. China Petroleum Machinery, 2018, 46(3): 78-83. |
| [12] |
白堂博, 张来斌, 王旭铎, 等. 基于SAX的关联规则挖掘方法在故障诊断中的应用[J]. 石油机械, 2017, 45(1): 70-74. BAI T B, ZHANG L B, WANG X D, et al. Application of sax-based association rule mining on fault diagnosis[J]. China Petroleum Machinery, 2017, 45(1): 70-74. |
| [13] |
姜民政, 段天玉, 张迪, 等. 基于RS-LVQ的同井注采系统故障诊断研究[J]. 石油机械, 2018, 46(3): 95-99. JIANG M Z, DUAN T Y, ZHANG D, et al. RS-LVQ-based fault diagnosis of the injection-produetion system[J]. China Petroleum Machinery, 2018, 46(3): 95-99. |
| [14] |
CAI B P, LIU Y H, FAN Q. Multi-source information fusion based fault diagnosis of ground-source heat pump using Bayesian network[J]. Applied Energy, 2014(114): 1-9. |
| [15] |
YODO N, WANG P. Resilience modeling and quantification for engineered systems using Bayesian networks[J]. Journal of Mechanical Design, 2016(3): 031404. |
| [16] |
LI W, POUPART P, BEEK P. Exploiting structure in weighted model counting approaches to probabilistic inference[J]. Journal of Artificial Intelligence Research, 2011, 40: 729-765. DOI:10.1613/jair.3232 |



