2. 中国石油集团工程技术研究有限公司
2. CNPC Engineering Technology R & D Company Limited
0 引言
水下遥控机器人(remotely operated vehicle,ROV)的定点悬停控制是其在复杂环境下是否能够顺利完成相应任务的重要技术之一。如对海底石油管线巡航检测、导管架检查以及对深海探测等,都需要ROV具有良好的稳定悬停能力。在复杂的海洋环境和高强度的工作条件下,针对ROV定点悬停相关控制方法的控制性能对比分析研究还相对较少,为了便于ROV在工程实践时对控制方法的选择,对ROV常用的几种控制方法进行性能对比分析研究便具有重要意义。
对于水下机器人稳定悬停的控制方法,国内外许多学者的已取得了大量研究成果:文献[1-4]分别采用模糊PID控制方法、一种简化的滑模控制方法、鲁棒H∞控制方法以及带约束的广义预测控制方法实现了水下机器人的深度自动控制,并获得了良好效果;文献[5]使用自适应模糊滑模控制对小型开架式ROV在浪涌干扰下的横摇运动进行了分析;文献[6]提及一种多变量自适应控制器,用于解决ROV在自动控制时运动模型不确定的问题;文献[7]提出了一种结合PID的广义预测优化算法,用于解决ROV在水中运动时受到波浪和海流等干扰造成系统稳定性差的问题;文献[8]应用了神经网络、滑模和遗传算法的组合控制方法对ROV的控制性能进行了研究。从这些成果中可以看出两种研究趋势:一种是将新的控制算法引进到ROV控制领域;另一种则是将2种或多种控制方法相结合,使原有控制方法的控制精度提升或适用范围扩大。他们都是通过仿真或试验的方式验证自己方法的可靠性和正确性,但都没有进行多个控制方法的控制性能对比。
从工程应用角度看,为了保证控制达到预期效果,需要控制系统具有良好的实时性,减少延时误差,这就要求控制系统的算法简单且可靠,因此简单性和可靠性应该成为控制器设计中的基本策略。由于ROV具有动态非线性、时变不定性和时滞后性等特点,再加上复杂的水动力和时刻变化的复杂海洋环境,使得线性控制器不再适用于ROV,而模糊控制不依赖控制系统的数学模型,控制形式简单易实现,且能实现非线性增益调整过程,因此常常在水下机器人中得到应用。笔者针对所设计的ROV进行稳定悬停观测这一实际工程问题,分别设计了PID控制器、模糊控制器和模糊PID控制器,对比分析了各控制器在复杂环境中进行定点悬停控制时的动态特性。研究成果对水下机器人工程实践指导具有重要意义。
1 ROV整体结构及工作要求笔者设计的开架式观测型ROV主要分上、下两层:顶层放置浮力模块(材料为玻璃微珠)和两个垂直推进器;第二层布置4个推进螺旋桨、电子舱和水下摄像系统等。整机质量为88 kg,其主尺寸(长×宽×高)为0.800 m×0.760 m×0.575 m,水平面推进器和纵向的布置夹角为30°,垂直面推进器与水平面的布置夹角为0°,水平面推进器推力矢量对质心的布置力臂为0.25 m,对Z轴的转动惯量为16 kg/m2。技术指标为:①最大工作深度100 m;②最大作业海况4级;③艏向闭环控制精度为±3°;④深度闭环控制精度为±0.1 m。笔者进行了一系列水动力仿真试验,取得了水动力系数,经过数值处理和无因次换算后得到的部分水动力系数如表 1所示。
| 项目 | 数值/(10-3) |
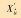
|
-84.0 |
| Xu′ | -163.0 |
| Xu|u|′ | -150.0 |
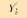
|
-39.0 |
| Yv′ | -263.9 |
| Yv|v|′ | -261.7 |
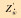
|
-112.2 |
| Zw′ | -317.6 |
| Zw|w|′ | -304.1 |
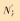
|
-5.0 |
| Nr′ | -57.4 |
| Nr|r|′ | -54.4 |
表 1中: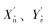
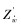
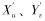
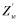
笔者以正在研制的观测型水下机器人为研究对象,其设计目的是进行导管架检测。为研究的简便和统一性,文中的坐标系、名词和符号均采用国际水池会议(ITTC)推荐的坐标系统。水下机器人的运动模型通常采用两套右手坐标系统:一套是固定坐标系E-ξηζ,另一套是运动坐标系O-xyz(见图 1)。为达到定点悬停的控制要求,将ROV的空间运动分为水平面运动(ξEη)和垂直面运动(ξEζ)。在水平面中对ROV进行定位控制,即在惯性坐标下保持ξ、η和艏向角ψ不变。在垂直面中对ROV进行定深控制,即在惯性坐标下保持ζ不变。

|
| 图 1 固定坐标系和运动坐标系 Fig.1 Fixed coordinate system and motion coordinate system |
ROV在水下运动是一种6自由度的空间运动,其空间运动方程包含了3个轴向移动方程和3个绕轴向转动方程[9],在其基础上根据所研究ROV对定位、定深的机动能力需求做相应修改和简化,且不对横摇和纵倾做控制。忽略垂直面对水平面的一些影响,并忽略模型中一些高阶项和外部环境力等影响,得到了该ROV适用的4自由度运动方程,其动力学方程为[10]:
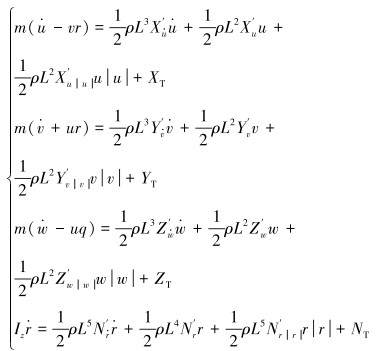
|
(1) |
式中:m为ROV的质量;ρ为水的密度;L为运载器的长度;Iz为ROV对Oz轴的转动惯量;u、v、w和r为ROV的纵向、横向、垂向线速度和艏向角速度;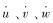
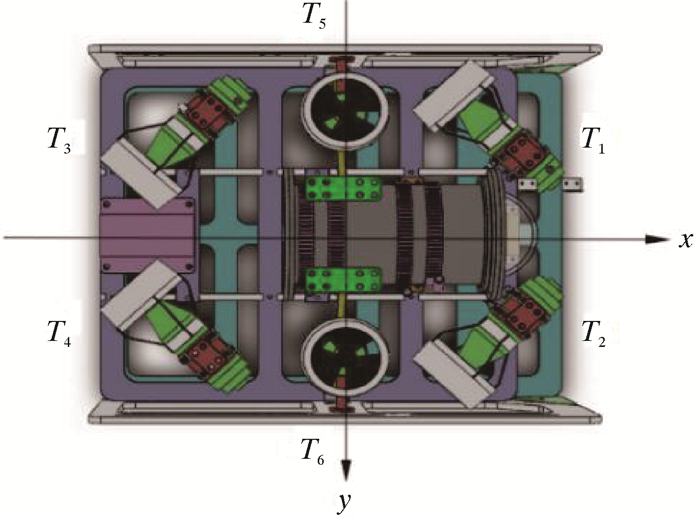
为实现设计所需的操纵性能,该ROV配置6台直流无刷螺旋桨,其中2台推进器以垂直布置在顶部两侧,4台推进器以X型互相垂直布置在水平面内(见图 2),以实现高效的矢量推进性能,达到ROV设计需求的纵向、横向、垂向运动和艏向转动的能力。
|
| 图 2 ROV推进器布置图 Fig.2 ROV thruster layout |
设6个推进器的推力分别为T1、T2、T3、T4、T5和T6,可以用矩阵表示为TJ=[T1 T2 T3 T4 T5 T6]T,与ROV所需推力的矢量矩阵FJ=[XT YT ZT NT]T的关系为:
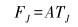
|
(2) |
式中:A为与推进器装配位置相关的推力转换矩阵,可以表示为:

|
(3) |
式中:α为水平面推进器与纵向的布置夹角,c为布置力臂。
ROV运动方程需要的是各运动矢量方向上的推力和力矩,而工程上控制的是各推进器的推进力,需要转换矩阵A的伪逆矩阵A+,从矢量推力和力矩反向计算出各推进器所需的推力为:
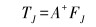
|
(4) |
采用各推进器推力TJ表示的ROV运动模型的状态方程为:
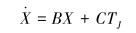
|
(5) |
式中:X=[u v w r]T,B=M-1P,C=M-1A。
其中,
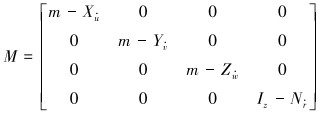
|
(6) |
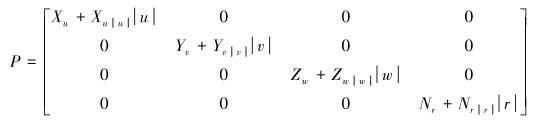
|
(7) |
水下机器人在近水面航行时,主要受海流和波浪影响。对于均匀流速下水下机器人计算一般是用水下机器人相对海流的相对速度代替运动模型中的相应速度项。设来流平行于大地坐标系的水平面,海流流速为定值,求得相对流速为[11]:
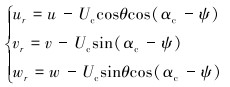
|
(8) |
式中:Uc为海流流速,αc为流向角,Ψ为艏向角。
将式(8)带入式(1)后便可得到海流情况下水下机器人的动力学模型。
2.2.2 海浪干扰水下机器人在近水面运动时,波浪力占其干扰力的主要部分,因此在进行受力分析时除了要考虑深水中固有的静力、水动力和螺旋桨推力外,还要考虑艇体受到的波浪力。理论计算主要是根据波浪力相关理论,建立数学模型并求解得到波浪力,一般将其分为一阶波浪力和二阶波浪力分别进行研究讨论[12]。在一阶波浪力的作用下,水下机器人将做横摇、纵摇和垂荡等摇荡运动,而二阶波浪力会产生一个向上的恒力(波吸力),对定深控制造成影响。一阶波浪力和力矩的确定方法如下[13]:
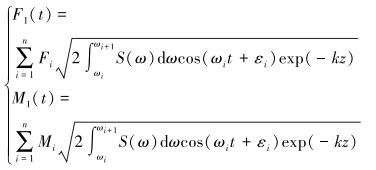
|
(9) |
式中:Fi、Mi为与波高、水下机器人宽度有关的系数,k为一阶波浪力和力矩随深度变化的衰减率,z为当前潜艇距水面深度,S(ω)为波浪谱密度,ωi为第i各组成波的角频率,εi为第i个组成波的初始相位,一般取值范围为(0, 2π)区间内的随机数。
二阶波浪力和力矩的确定方法如下[14]:
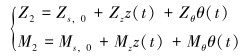
|
(10) |
式中:z为水下机器人所处深度,θ为水下机器人的纵倾角度,Zs, 0、Zz、Zθ、Ms, 0、Mz和Mθ为波浪干扰力系数,系数的详细计算过程参考文献[14]。
3 3种控制方式控制性能分析为充分测试各个控制器在该观测型ROV实际复杂工作环境下的定点悬停的控制效果,本文分别进行近水面区域和相对较深区域定点悬停控制。为了保证水下系统能够得到清晰的观测效果,一般使水下摄像系统离观测物3~5 m,晃动线速度小于5 m/s,艏向角偏差小于5°[15]。为了实现ROV更稳定的观测效果,取艏向闭环控制精度为±3°,深度闭环控制精度为±0.1 m,每组仿真以前,ROV的初始速度和艏向角均为0,海流流速为1 m/s,
3.1 常规PID控制常规PID控制器控制过程如图 3所示。
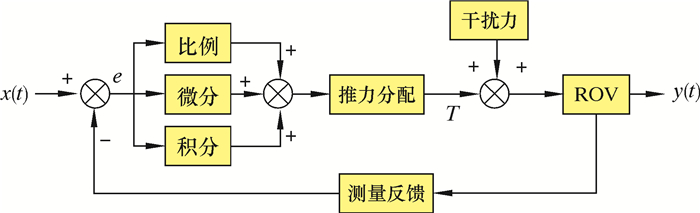
|
| 图 3 常规PID控制器控制过程 Fig.3 Schematic diagram of conventional PID control |
PID控制器是一种线性结构控制器,它由给定值x(t)与实际输出值y(t)运算得到偏差值e,将偏差的比例(P)、积分(I)、微分(D)线性组合得到了控制量,对被控对象进行控制。每个自由度单独使用一个控制器:x轴方向,KP=70,KI=1,KD=40;y轴方向,KP=130,KI=1,KD=11;深度方向,KP=70,KI=5,KD=15;艏向,KP=80,KI=1,KD=5。
3.1.1 近水面区域定点悬停在近水面时,ROV容易受到海水表面浪和流的复合影响,所以垂直面(ξEζ)内添加余弦组成的随机信号来模拟ROV在运动时所受到的外界环境干扰。为了保证海上作业人员的安全,一般要求作业是海况不超过5级[16]。假设ROV在4级海况下工作,波浪力为2 000 N[17],期望定深为5 m,艏向角为45°,即保持ROV的状态η=[0, 0, 5, 45],仿真结果如图 4和图 5所示。
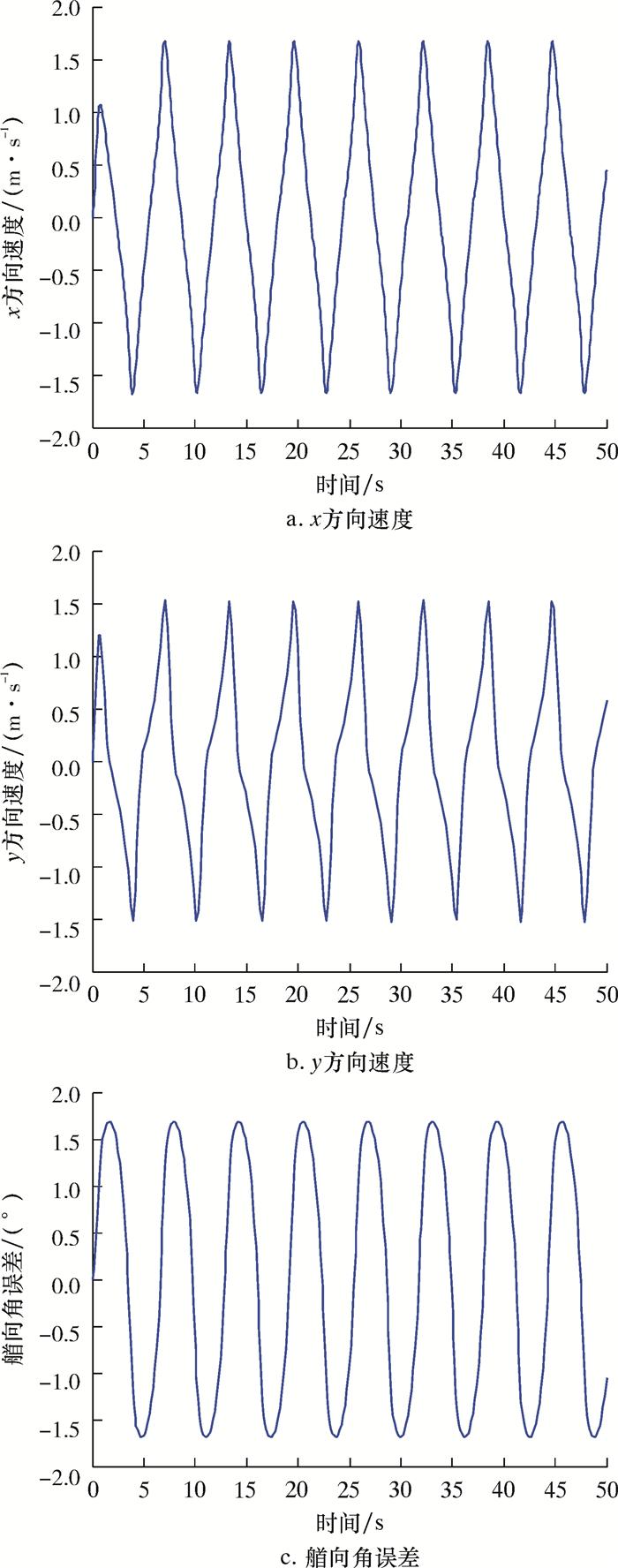
|
| 图 4 水平面定位控制仿真曲线 Fig.4 Control simulation curve of positioning on horizontal plane |
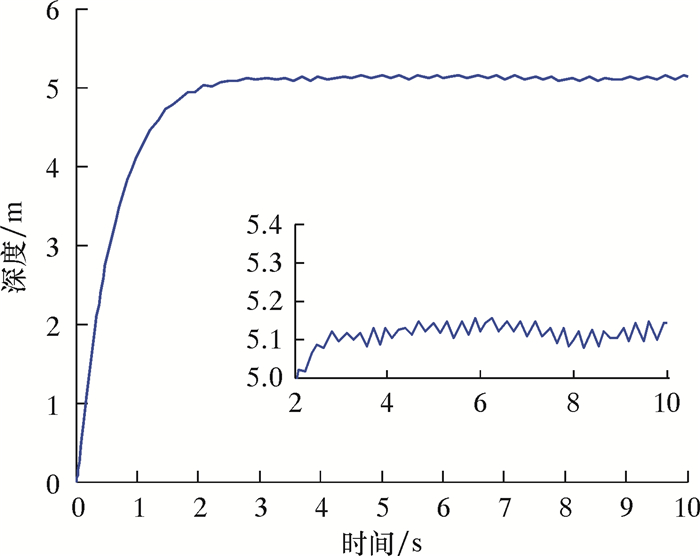
|
| 图 5 垂直面定深5 m控制仿真曲线 Fig.5 Control simulation curve of vertical plane positioning at the depth 5 m |
由图 4可以看出,在一阶波浪力的影响下,x和y方向都产生了1.5 m/s左右的晃动线速度,但小于要求指标5 m/s,艏向角产生了±1.6°的误差,也小于要求的±3°的要求。由于一阶波浪力是高频振荡波,而运载器质量较大,是一个惯性很大的系统,可以将其视为一个低通滤波器,对一阶波浪力具有衰减的作用,虽然会引起运载器6自由度的运动,但通常都在安全范围内。
由图 5可以看出,由于二阶波浪力会产生一个向上的恒力,所以在二阶波浪力的影响下,水下机器人的深度误差超过了±0.1 m的要求,且存在强烈的振颤现象。PID控制器在该海洋环境下无法满足近水面定点悬停的控制要求。
3.1.2 相对较深区域定点悬停由于ROV在相对较深区域运动时,ROV的水平面运动基本不受海水表面流和浪的影响,垂直面运动主要受到涌这样的瞬时干扰,所以在Eζ上添加一个瞬时干扰力来模拟涌的作用。多次仿真试验后取干扰力F为50、100和150 N,干扰起始时间为6 s,持续2 s,期望定深20 m,仿真结果如图 6所示。
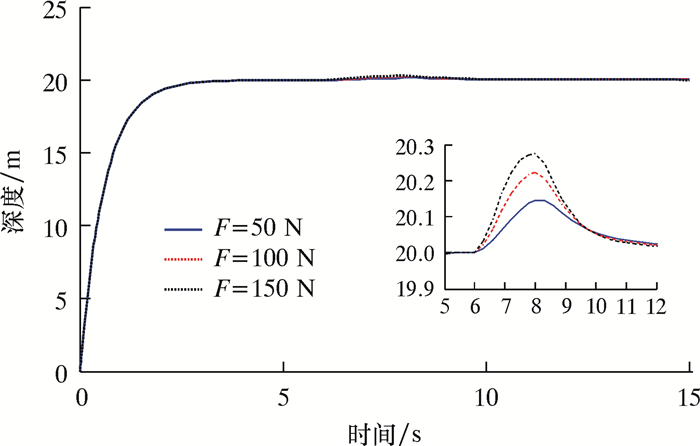
|
| 图 6 垂直面定深20 m控制仿真曲线 Fig.6 Control simulation curve of vertical plane positioning at the depth 20 m |
由图 6可以看出,ROV在50 N的干扰力下就不能满足深度误差±0.1 m的控制要求,PID控制器在相对较深海域定点悬停时适应能力差。
因此,针对以上情况,需要一个抗干扰能力和适应能力都强的控制器来满足定点悬停的控制要求。
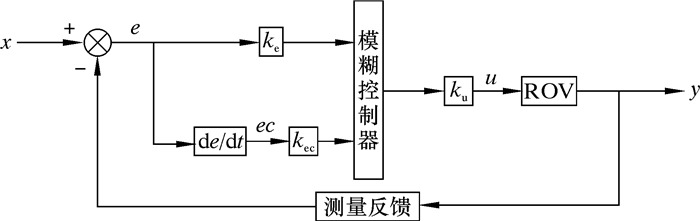
3.2 模糊控制器笔者采用Mamdani型模糊控制器,其控制示意图如图 7所示。
|
| 图 7 模糊控制示意图 Fig.7 Schematic diagram of fuzzy control |
图 7中:e和ec分别表示误差和误差的变化率,ke、kec为量化因子,ku为比例因子。由图 7可得,该模糊控制器是以e和ec为输入,u为输出的两输入单输出控制器。各部分的具体设计如下。
3.2.1 模糊化和反模糊化设计输入输出的语言变量集取为:
{负大,负中,负小,零,正小,正中,正大},即{NB,NM,NS,ZE,PS,PM,PB}。
模糊量化论域为:{-3,-2,-1,0,1,2,3}。
3.2.2 量化因子设计假设x的物理论域X1=[a, b]且a≠b,模糊论域为N1=[-n1, n1],则这时量化因子为ke=2n1/|b-a|;同样,对于输入量ec设它的物理论域X2=[-x2, x2],模糊论域为N2=[-n2, n2],这时量化因子为kec=n2/x2。
3.2.3 模糊规则库设计。对应不同输入量ec和ke时,输出量u的值即模糊控制规则如表 2所示,这样就完成了Mamdani型模糊控制器的设计。
| e | ec | ||||||
| NB | NM | NS | ZE | PS | PM | PB | |
| NB | NB | NB | NB | NM | NS | ZE | ZE |
| NM | NB | NB | NM | NS | ZE | ZE | PS |
| NS | NB | NM | NM | NS | ZE | PS | PM |
| ZE | NB | NM | NS | ZE | PS | PM | PB |
| PS | NM | NS | ZE | PS | PM | PM | PB |
| PM | NS | ZE | PS | PS | PB | PB | PB |
| PB | ZE | PS | PM | PM | PB | PB | PB |
3.2.4 近水面区域定点悬停
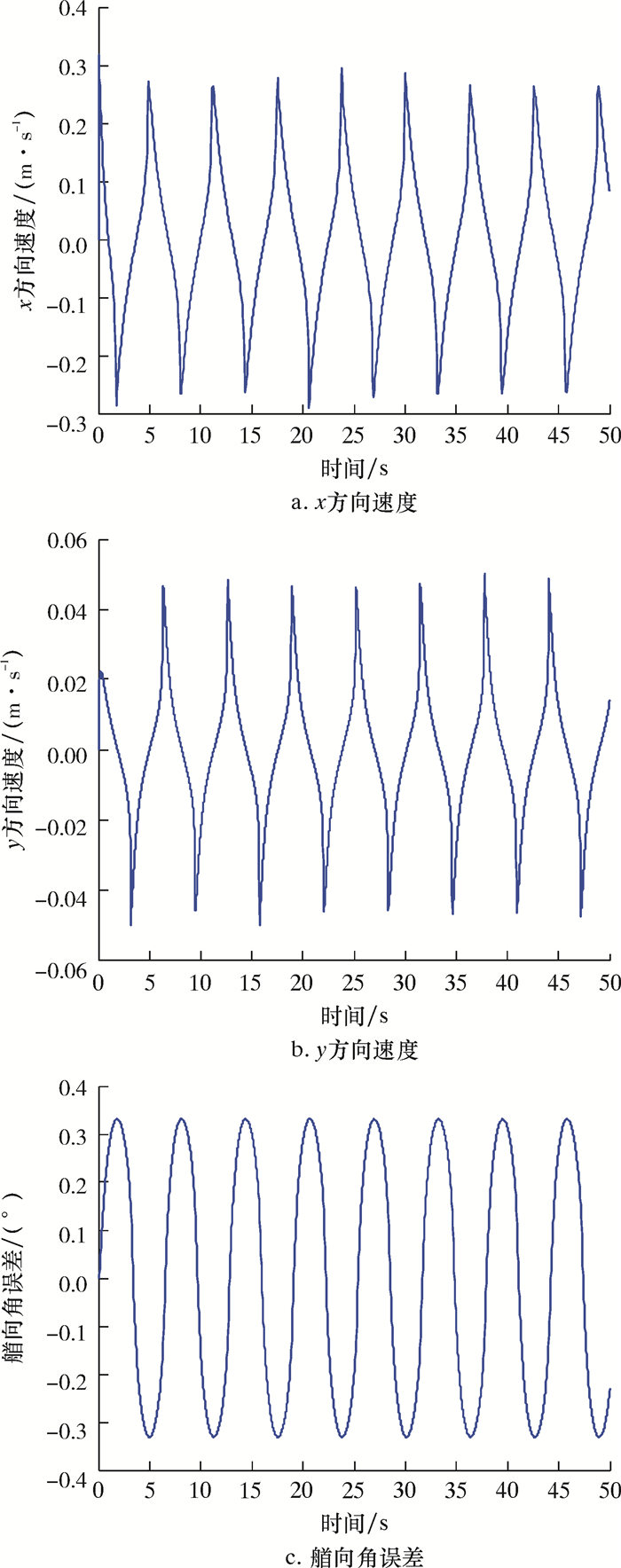
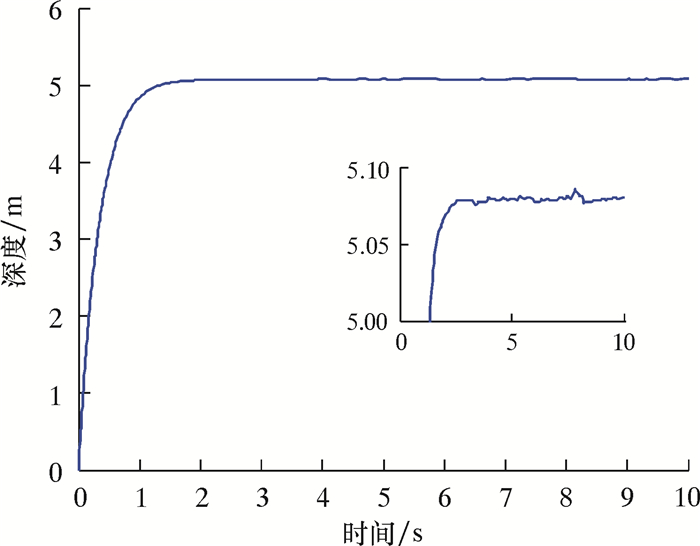
外界环境条件和工作指标都与PID控制器相同,即假设ROV在4级海况下工作,期望定深为5 m,艏向角为45°,即保持ROV的状态η=[0, 0, 5, 45],仿真结果如图 8和图 9所示。
|
| 图 8 水平面定位控制仿真曲线 Fig.8 Control simulation curve of positioning on horizontal plane |
|
| 图 9 垂直面定深5 m控制仿真曲线 Fig.9 Control simulation curve of vertical plane positioning at the depth 5 m |
由图 8可以看出:在一阶波浪力的影响下,x方向和y方向分别产生了0.28和0.05 m/s左右的晃动线速度,远远小于要求指标5 m/s;艏向角产生了±0.3°左右的误差,也远远小于±3°的要求,模糊控制器的控制效果相比PID控制器的控制效果有大幅度的提升。
由图 9可以看出,即使在二阶波浪力的影响下,ROV也能保持在水深5 m处悬停,并且误差在0.08 m,小于±0.1 m的要求,满足了控制要求,但由于缺乏积分项,无法消除静态误差。
相比PID控制器,模糊控制器不仅满足了近水面定点悬停的控制要求,而且提高了ROV的抗干扰能力,为ROV上的相关设备和传感器提供了更加稳定的工作条件,使其能够获得更加清晰的观测图像,提高了整体的控制质量。
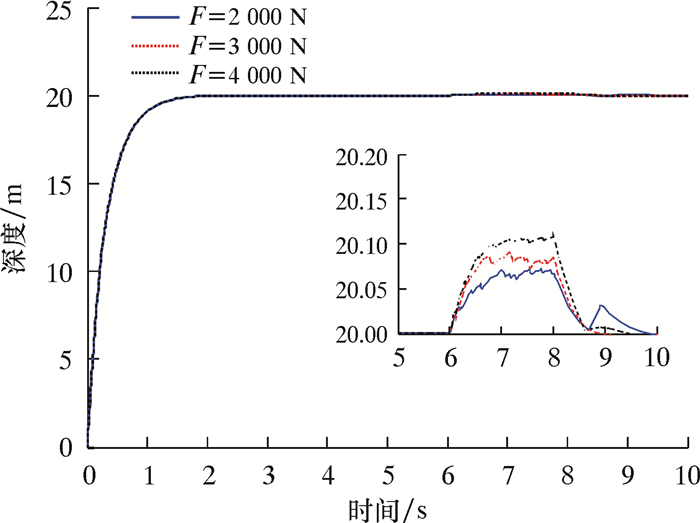
3.2.5 相对较深区域定点悬停外界环境条件和工作指标都与PID控制器相同,即在Eζ上添加一个瞬时干扰力来模拟涌的作用,仿真时若干扰力取为50、100和150 N,则模糊控制的图像基本没有改变,所以为了便于分析,多次仿真后取干扰力为2 000、3 000和4 000 N,干扰起始时间为6 s,持续2 s,期望定深20 m,仿真结果如图 10所示。
|
| 图 10 垂直面定深20 m控制仿真曲线 Fig.10 Control simulation curve of vertical plane positioning at the depth 20 m |
由图 10可以看出,ROV要在4 000 N干扰力时,才会不满足深度误差±0.1 m的控制要求,相比于PID控制器在50 N时就不能满足工作要求的情况,模糊控制器的控制性能明显大幅度提升,提高了ROV在相对较深区域定点悬停的适应能力和抗干扰能力。
与PID控制器相比,模糊控制器具有更强的抗干扰能力和适应能力,能够很好地完成定点悬停的控制要求。但由于模糊控制缺乏积分项,不能去除稳态误差,无法实现较为精准的控制要求,而PID能够实现较高的控制精度,但抗干扰能力和适应能力弱,所以将两者结合后,优势互补,使控制系统具有较佳的控制效果。
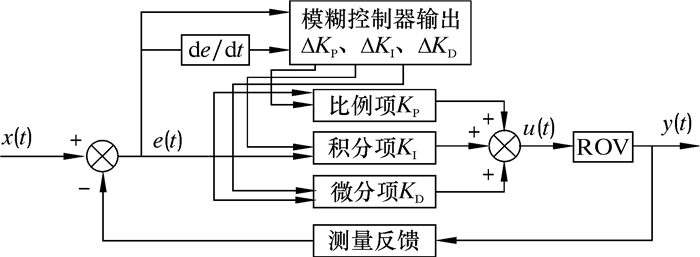
3.3 模糊PID控制器针对ROV的控制需求,应用结合模糊控制原理的PID控制器来解决实际工程中的需要,其控制结构示意图如图 11所示。
|
| 图 11 模糊PID控制机构示意图 Fig.11 Schematic diagram of fuzzy PID control mechanism |
该系统由一个PID控制器和模糊控制器组合而成,模糊控制器以偏差e和偏差变化率ec作为输入,利用模糊控制规则在线对PID参数进行实时的修改,实时调整输出3个参数ΔKP、ΔKI和ΔKD,从而可以根据不同时刻系统对PID参数的要求,输出所需要的PID参数。通过多次操作经验或多次操作的数据处理,结合理论分析可以归纳出偏差e、偏差变化率ec跟PID调节的3个参数KP、KI和KKD间存在的关系。
3.3.1 当|e(t)|较大时此时,为加快系统的响应速度,应取较大的KP,当然KP不能过大,否则会导致系统不稳定;为避免系统在开始时可能引起的超范围控制作用,应取较小的KD,以便加快系统响应。
3.3.2 当|e(t)|处于中等大小时此时,应取较小的KP,使系统响应的超调变小,同时可适当增加一点KI,但不能过大。
3.3.3 当|e(t)|较小时此时,可取较大的KP和KI。为避免系统在平衡点出现震荡,KD取值应恰当。
基于以上总结的输入变量e与3个参数KP、KI和KD间的定性关系,结合工程技术人员的分析和实际操作经验,考虑偏差变化率|ec(t)|的影响,得出3个输出参数ΔKP、ΔKI和ΔKD的模糊规则如表 3、表 4和表 5所示,这样就完成了模糊PID控制器的设计。
| e | ec | ||||||
| NB | NM | NS | ZE | PS | PM | PB | |
| NB | PB | PB | PM | PM | PS | ZE | ZE |
| NM | PB | PB | PM | PS | PS | ZE | NS |
| NS | PM | PM | PM | PS | ZE | NS | NS |
| ZE | PM | PM | PS | ZE | NS | NM | NM |
| PS | PS | PS | ZE | NS | NS | NM | NM |
| PM | PS | ZE | NS | NM | NM | NM | NB |
| PB | ZE | ZE | NM | NM | NM | NB | NB |
| e | ec | ||||||
| NB | NM | NS | ZE | PS | PM | PB | |
| NB | NB | NB | NM | NM | NS | ZE | ZE |
| NM | NB | NB | NM | NS | NS | ZE | ZE |
| NS | NB | NM | NS | NS | ZE | PS | PS |
| ZE | NM | NM | NS | ZE | PS | PM | PM |
| PS | NM | NS | ZE | PS | PS | PM | PB |
| PM | ZE | ZE | PS | PS | PM | PB | PB |
| PB | ZE | ZE | PS | PM | PM | PB | PB |
| e | ec | ||||||
| NB | NM | NS | ZE | PS | PM | PB | |
| NB | PS | NS | NB | NB | NB | NM | PS |
| NM | PS | NS | NB | NM | NM | NS | ZE |
| NS | ZE | NS | NM | NM | NS | NS | ZE |
| ZE | ZE | NS | NS | NS | NS | NS | ZE |
| PS | ZE | ZE | ZE | ZE | ZE | ZE | ZE |
| PM | PB | NS | PS | PS | PS | PS | PB |
| PB | PB | PM | PM | PM | PS | PS | PB |
3.3.4 近水面区域定点悬停
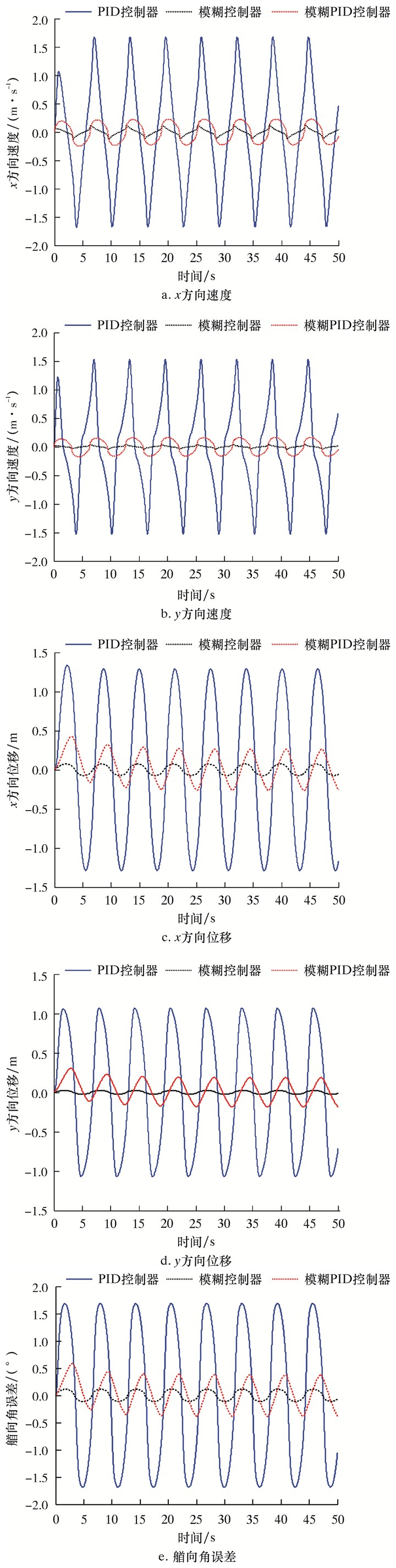
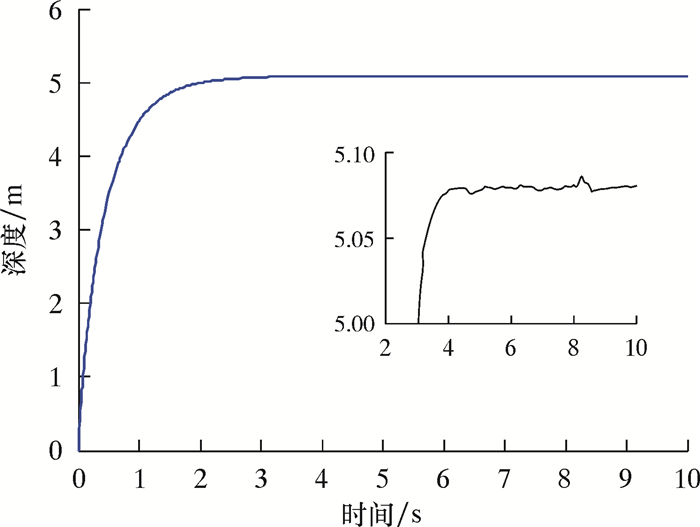
假设ROV分别在4级海况下工作,期望定深为5 m,艏向角为45°,即保持ROV的状态η=[0, 0, 5, 45],仿真结果如图 12和图 13所示。
|
| 图 12 水平面定位控制仿真曲线 Fig.12 Control simulation curve of positioning on horizontal plane |
|
| 图 13 垂直面定深5 m控制仿真曲线 Fig.13 Control simulation curve of vertical plane positioning at the depth 5 m |
由图 12和图 13可以看出,模糊PID和模糊控制一样都能较好地实现近水面区域定点悬停,模糊PID不仅提高了PID的抗干扰能力,而且弥补了单独使用模糊器时不能消除静态误差的不足。模糊PID中虽然对专家知识和操作经验进行了规则构造,但是在挑选隶属函数、解模糊化和量化因子调整等方面还没有全面、合理的判断依据,因此可能存在更好的控制参数来提高模糊PID的控制效果。但就目前来看,模糊PID控制器没有模糊控制器的抗干扰能力强。
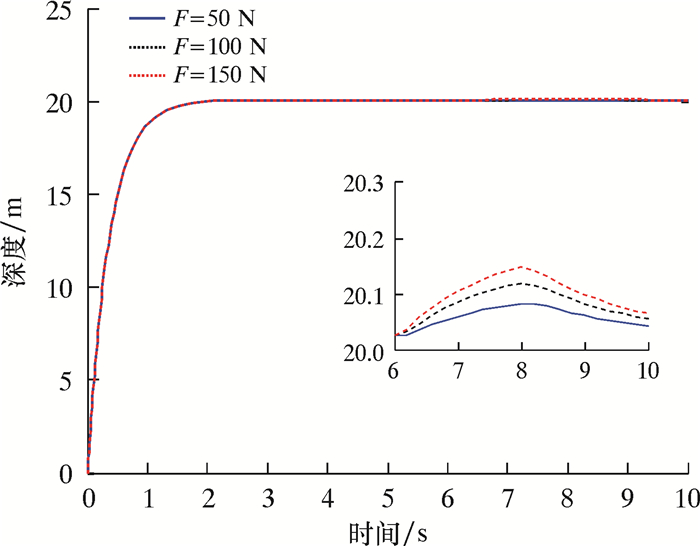
3.3.5 相对较深区域定点悬停ROV在相对较深区域运动时,ROV的水平面运动基本不受海水表面流和浪的影响,垂直面运动主要受到涌这样的瞬时干扰,所以在Eζ上添加一个瞬时干扰力来模拟涌的作用,多次仿真试验后取干扰力为50、100和150 N,干扰起始时间为6 s,持续2 s,期望定深20 m,仿真结果如图 14所示。
|
| 图 14 垂直面定深20 m控制仿真曲线 Fig.14 Control simulation curve of vertical plane positioning at the depth 20 m |
由图 14可以看出,ROV在100 N干扰力时不能满足深度误差±0.1 m的控制要求,与PID控制器相比,抗干扰能力有所提升,与模糊控制相比,消除了稳态误差,图像较为平滑,改善了ROV在相对较深海域定点悬停时抗干扰能力,但抗干扰性能还是远不及模糊控制器。
4 结论及建议(1) 研究了开架式观测型ROV定点悬停控制方法,将PID控制器、模糊控制器和模糊PID控制器分别用于近水面区域和相对较深区域进行稳定悬停控制研究,并与常规PID进行了仿真对比。
(2) 在定点悬停控制中,PID控制器适应能力差,抗干扰能力弱,对环境变化敏感;模糊控制器在复杂环境中具有良好的响应特性和抗干扰能力,但存在稳态误差,无法实现精准控制;模糊PID综合了两者的优势,既提高了PID控制器的响应速度和抗干扰能力,又弥补了模糊控制存在稳态误差的缺点,但抗干扰性能还是远不及模糊控制器。
(3) 当控制精度要求不是很高时,建议使用模糊控制器更好,当需要精准控制且控制误差在允许范围内时,建议使用模糊PID控制器。
| [1] |
魏延辉, 张皓渊. 水下作业型ROV定深控制系统的设计[J]. 中国科技论文, 2016, 11(8): 898-903. WEI Y H, ZHANG H Y. Design of the depth control system for underwater work-class ROV[J]. China Sciencepaper, 2016, 11(8): 898-903. DOI:10.3969/j.issn.2095-2783.2016.08.012 |
| [2] |
NAG A, PATEL S S, KISHORE K, et al. A robust H-infinity based depth control of an autonomous underwater vehicle[C]//2013 International Conference on Advanced Electronic System.Pilani: IEEE Computer Society, 2013: 68-73.
|
| [3] |
WATSON S A, GREEN P N. Depth control formicro-autonomous underwater vehicles:simulation and experimention[J]. International Journal of Advanced Robotic System, 2014, 11(1): 1-10. DOI:10.5772/56810 |
| [4] |
GENG T, ZHAO J. Generalized predictive control withconstraints for autonomous underwater vehicle depth control[C]//Modelling, Identification & Control(ICMIC)2012 Proceedings of International Conference on IEEE, 2012: 618-623.
|
| [5] |
刘和平, 龚振邦, 李敏, 等. 水下机器人浪涌中横摇角的模糊滑模控制[J]. 武汉理工大学学报, 2009, 31(14): 122-133. LIU H P, GONG Z B, LI M, et al. Fuzzy sliding mode control on the rolling of underwater robot in wave[J]. Journal of Wuhan University of Technology, 2009, 31(14): 122-133. DOI:10.3963/j.issn.1671-4431.2009.14.031 |
| [6] |
袁晓宇. 一种基于PID算法的ROV运动控制的研究[J]. 自动化博览, 2012(7): 76-79. YUAN X Y. Numeric PID arithmetic in remotely operated vehicle sailing control[J]. Automation Panorama, 2012(7): 76-79. DOI:10.3969/j.issn.1003-0492.2012.07.021 |
| [7] |
刘慧婷, 冯金金, 张明. 水下机器人操纵系统优化控制研究[J]. 计算机仿真, 2016, 33(5): 299-303. LIU H T, FENG J J, ZHANG M. Researchon optimal control of underwater robot control system[J]. Computer Simulation, 2016, 33(5): 299-303. DOI:10.3969/j.issn.1006-9348.2016.05.065 |
| [8] |
JAVADI-MOGHADDAM J, BAGHERI A. An adaptiveneurofuzzy sliding mode based genetic algorithm control system for underwater remotely operated vehicle[J]. Expert Syst, 2010, 37(3): 647-660. |
| [9] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995.
|
| [10] |
刘可峰, 连琏, 曹俊亮, 等. 基于模糊PID方法的ROV操纵控制仿真[J]. 江苏科技大学学报, 2015, 29(1): 70-75. LIU K F, LIAN L, CAO J L, et al. Simulation on manoeuvre and control of ROV based on fuzzy PID algorithm[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2015, 29(1): 70-75. DOI:10.3969/j.issn.1673-4807.2015.01.012 |
| [11] |
常文君, 刘建成, 于华南, 等. 水下机器人运动控制与仿真的数学模型[J]. 船舶工程, 2002(3): 58-60. CHANG W J, LIU J C, YU H N, et al. A mathematical model for motion control and simulation of underwater vehicle[J]. Ship Engineering, 2002(3): 58-60. DOI:10.3969/j.issn.1000-6982.2002.03.015 |
| [12] |
冯学知, 蒋强强, 缪泉明, 等. 潜体波浪中近水面不同潜深和航向时运动和波浪力计算[J]. 船舶力学, 2002, 6(2): 1-14. FENG X Z, JIANG Q Q, MIAO Q M, et al. Computation of motion and wave forces for a submarine running near free surface in different depth of immersion and direction[J]. Journal of Ship Mechanics, 2002, 6(2): 1-14. DOI:10.3969/j.issn.1007-7294.2002.02.001 |
| [13] |
常赛.潜艇近水面航行控制方法研究[D].哈尔滨: 哈尔滨工程大学, 2011. CHANG S. Research on the control ofsubmarines near the surface[D]. Harbin: Harbin Engineering University, 2011. |
| [14] |
王鹢, 王文武, 孙枫, 等. 干扰力作用下潜艇近水面运动的仿真[J]. 系统仿真学报, 2003, 15(1): 84-87. WANG Y, WANG W W, SUN F, et al. Simulation of submarine near-surface motion under disturbance force[J]. Journal of System Simulation, 2003, 15(1): 84-87. DOI:10.3969/j.issn.1004-731X.2003.01.023 |
| [15] |
刘泽发.观测型ROV航行控制系统设计及运动控制技术研究[D].杭州: 浙江大学, 2015. LIU Z F. Development of navigation controlsystem and research on the motion control technique of observation-class ROV[D]. Hangzhou: Zhejiang University, 2015. |
| [16] |
hp_chen70.普氏风力等级表及海况等级表[EB/OL].[2018-05-21], https://wenku.baidu.com/view/39cec065ee06eff9aef8075f.html.
|
| [17] |
潘瑛, 徐德民. 基于Matlab的AUV近水面运动模型的建立与仿真[J]. 船舶工程, 2003, 2(5): 15-18. PAN Y, XU D M. Modeling and simulation of AUV in 6DOF motion near water surface by Matlab[J]. Ship Engineering, 2003, 2(5): 15-18. DOI:10.3969/j.issn.1000-6982.2003.05.004 |



