2. 中海油研究总院有限责任公司
2. CNOOC Research Institute Co., Ltd
0 引言
深水钻井井筒温度场分布对井筒压力控制、钻井液热物性参数以及井壁稳定等具有显著的影响。因此,准确预测井筒温度分布对安全快速钻井具有重要意义。国内外学者[1-5]针对井筒循环温度场进行了深入研究。L.R.RAYMOND[6]最早基于能量平衡原理建立了井筒地层传热数值模型。G.P.WILLHITE[7]首次提出了综合传热系数。J.ROMERO等[8]综合考虑了钻井过程中排量、时间和海洋环境对井筒温度场的影响,建立了井筒温度场计算的新方法。E.KARSTAD等[9]基于连续性方程和能量守恒定律,建立了循环过程中温度场模型来研究井筒流体与地层的热交换机理。宋洵成等[10]建立了深水环境中循环温度分布模型,探究了海水对井筒温度场的影响规律。夏环宇等[11]考虑突扩孔道流动的问题,研究了增压管线排量对深水钻井井筒温度场的影响规律。综上所述,尽管诸多学者对井筒温度场进行了大量研究,但针对增压管线流体引起的变质量流动所导致的井筒温度变化问题还未见到相关报道。因此,笔者考虑了深水钻井过程中增压管线流体进入井筒引起的变质量流动,基于质量和能量守恒原理,建立了井筒和地层不同区域的瞬态传热数学模型,并分析了增压管线排量和入口温度对井筒温度场的影响规律,以期为深水钻井过程中井筒温度场的预测提供理论参考。
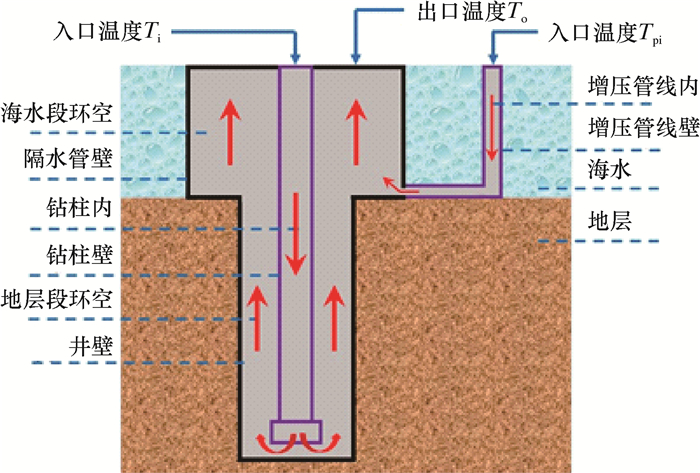
1 物理模型在深水钻井过程中,有增压管线的深水钻井系统物理模型如图 1所示。
|
| 图 1 有增压管线的深水钻井系统物理模型 Fig.1 Physical model of deepwater drilling system with boost line |
图 1中,钻井液以初始温度Ti流入钻柱,并沿着钻柱轴线向下流动,流至钻头时经过钻头水眼进入地层段环空内。钻井液沿井筒轴线继续在环空内向上流动,最终以温度To流出井口。此外,钻井液以初始温度Tpi流入增压管线,并沿增压管线向下流动,最后在泥线处进入隔水管环空内,与环空内上返的钻井液混合。在此过程中,钻柱内的流体、钻柱壁、环空内的流体、井壁、增压管线内的流体、增压管线壁、地层和海水均会在轴向和径向上进行热传递或热交换。
2 数学模型在建立数学模型之前,首先做以下基本假设:①忽略地层中垂向上的热传导,仅考虑水平方向的热传导。②忽略钻杆、套管和水泥环的热惯量。③地层内不存在流体的流动。④忽略钻井液轴向导热和钻井液的径向温度变化。
2.1 增压管线区域增压管线内流体体积单元的能量由3部分组成:①流体摩擦损失产生的热源项。②增压管线中的钻井流体向下流动引起的热对流。③流体与增压管线内壁在径向方向上的热传导。根据热力学第一定律,得到增压管线内的能量微分方程:
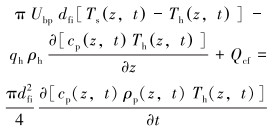
|
(1) |
式中:dfi是增压管线内径, m; cp是增压管线的比热容, J/(kg·℃);Ubp是增压管线外壁到增压管线内壁的总传热系数, W/(m2·℃); Th、Ts分别是增压管线内钻井液温度和海水温度, ℃; ρp、ρh分别是增压管线和其中钻井液的密度, kg/m3; qh是增压管线中钻井液的排量, m3/s; Qcf是增压管线内的热源项, W。
2.2 钻柱区域钻柱内流体体积单元的能量由3部分组成[12]:①流体摩擦损失产生的热源项。②钻柱中的钻井流体向下流动引起的热对流。③流体与钻柱内壁在径向方向上的热传导。根据热力学第一定律,得到钻柱内的能量微分方程:
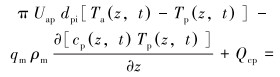
|
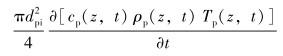
|
(2) |
式中:dpi是钻柱内径, m; Uap是钻柱外壁到钻柱内壁的总传热系数, W/(m2·℃); Tp、Ta分别是钻柱内钻井液温度和环空内钻井液温度, ℃; cp是钻柱的比热容, J/(kg·℃); ρp、ρm分别是钻柱和钻井液的密度, kg/m3; qm是钻井液的排量, m3/s; Qcp是钻柱内的热源项, W。
2.3 地层段环空区域地层段环空流体温度的影响因素主要由4部分组成:①流体摩擦损失产生的热源项。②环空中流体内部的热对流。③环空与钻柱外壁之间的热传导。④环空流体与套管或地层之间的热传导。根据热力学的第一定律,得到地层段环空内的能量微分方程:
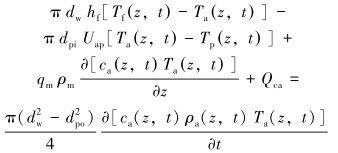
|
(3) |
式中:dpo、dw分别是钻柱内径和套管内径, m; hf是地层和套管的对流换热系数,W/(m2·℃); Tf是地层温度, ℃; ca是套管的比热容, J/(kg·℃); ρa是套管的密度, kg/m3; Qca是地层环空内的热源项, W。
2.4 海水段环空区域海水段环空流体温度的影响因素主要由5部分组成:①流体摩擦损失产生的热源项。②环空中流体内部的热对流。③环空与钻柱外壁之间的热传导。④环空流体与套管或海水之间的热传导。⑤增压管线中的流体和海水段环空流体的热对流。根据热力学的第一定律,得到海水段环空内的能量微分方程:
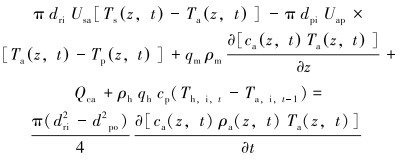
|
(4) |
式中:dri是钻柱内径和套管内径, m; Usa是海水和隔水管的综合对流换热系数, W/(m2·℃); Th, i, t是增压管线进入隔水管的位置处t时刻增压管线中混合钻井液的温度, ℃; Ta, i, t-1是增压管线进入隔水管的位置处t-1时刻环空中的钻井液温度, ℃, 并令Qch=ρhqhcp(Th, i, t-Ta, i, t-1)。
2.5 地层或海水区域地层段的能量微分方程为:
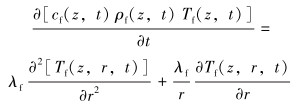
|
(5) |
海水段的能量微分方程为(假设海水静止):
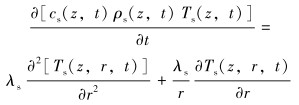
|
(6) |
式中:Tf、Ts分别是地层和海水的温度, ℃; cf、cs分别是地层和海水的比热容, J/(kg·℃); ρf、ρs分别是地层和海水的密度, kg/m3; λf、λs分别是地层和海水的导热系数, W/(m·℃)。
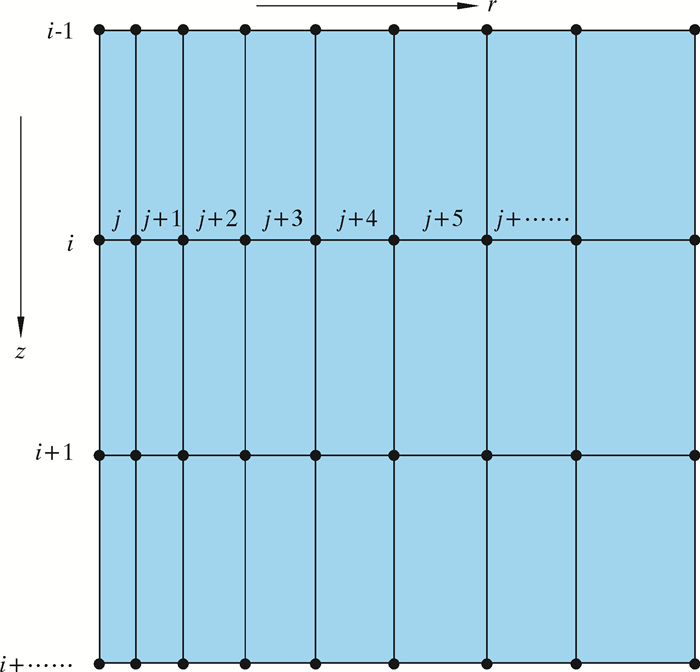
3 数学模型求解基于无条件稳定的Crank-Nicolson全隐式差分格式对上述不同区域的温度控制方程进行离散[13-14],网格划分如图 2所示。
|
| 图 2 井筒、海水和地层网格示意图 Fig.2 Grid schematic diagram of the wellbore, seawater and formation |
对增压管线内的能量微分方程(1)进行离散,则有:
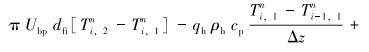
|
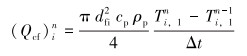
|
(7) |
对钻柱内的能量微分方程(2)进行离散,则有:
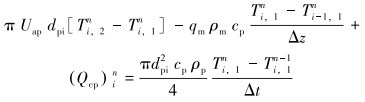
|
(8) |
对地层段环空内的能量微分方程(3)进行离散,则有:
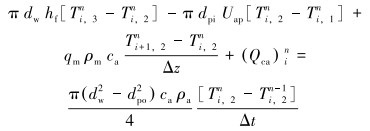
|
(9) |
对海水段环空内的能量微分方程(4)进行离散,则有:
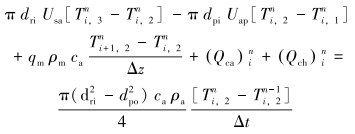
|
(10) |
对地层段的能量微分方程(5)进行离散,则有:
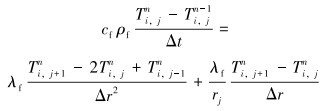
|
(11) |
对海水段的能量微分方程(6)进行离散,则有:
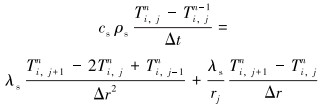
|
(12) |
一口井的具体参数如下:井深5 000 m,海水段1 500 m,钻柱内径108.6 mm,钻柱外径127.0 mm,隔水管内径533.4 mm,隔水管外径596.9 mm,直井井筒入口温度30 ℃,直井井筒钻井液排量30 L/s,地温梯度0.025 ℃/m。增压管线内径108.6 mm,外径127.0 mm,增压管线入口温度30 ℃,增压管线钻井液排量30 L/s。各介质热物理参数见表 1。
| 热物理参数 | 钻井液 | 海水 | 地层 | 钻柱 |
| 密度/(kg·m-3) | 1 500 | 1 030 | 2 640 | 780 |
| 导热系数/ (W·m-1·℃-1) | 1.73 | 0.60 | 2.25 | 43.75 |
| 比热容/ (J·kg-1·℃-1) | 1 365 | 3 890 | 837 | 400 |
4.2 井筒温度分布
环空和钻柱循环温度剖面随时间的变化分别如图 3和图 4所示。
|
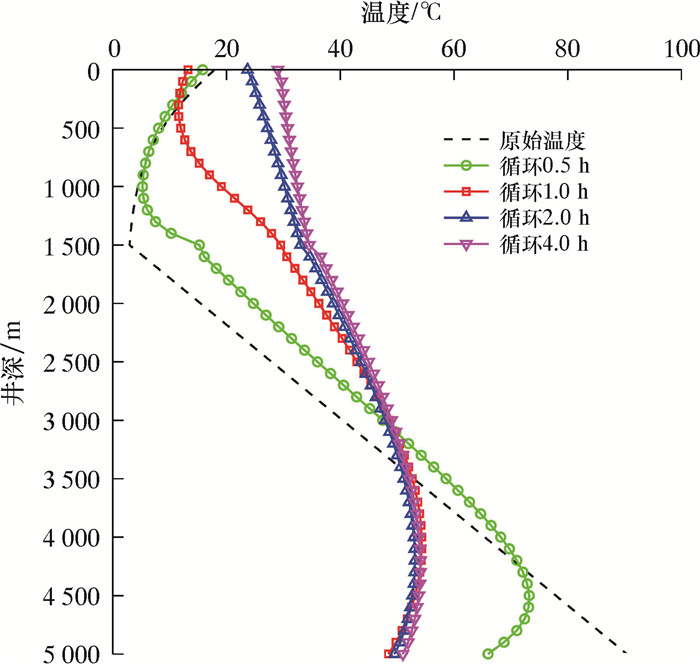
| 图 3 环空循环温度剖面随时间的变化 Fig.3 Variation of annulus circulation temperature profile with time |
|
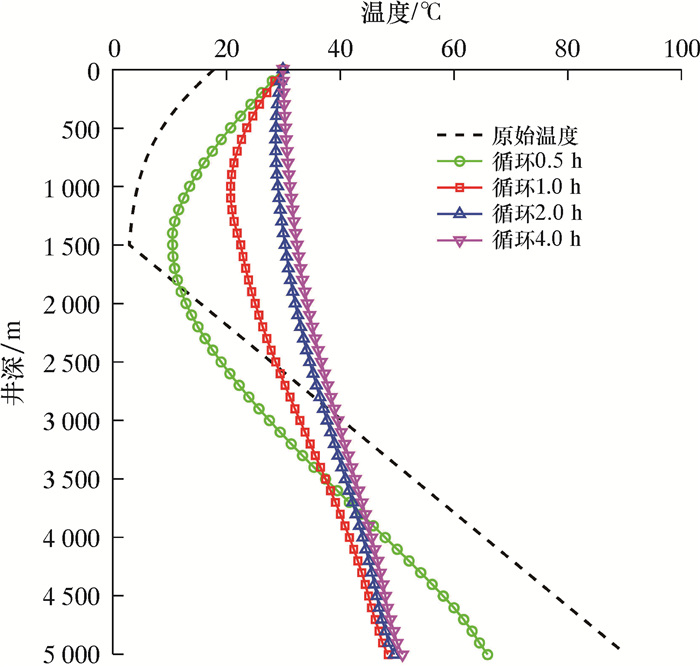
| 图 4 钻柱循环温度剖面随时间的变化 Fig.4 Variation of drill pipe circulation temperature profile with time |
由图 3可知,环空循环温度剖面存在两个临界井深(井深较小的称“第一临界井深”,井深较大的称为“第二临界井深”)。随着循环时间增加,两个临界井深之间的环空温度随之升高,而第一临界井深以上的环空温度和第二临界井深以下的环空温度先降低后升高。由图 4可知,存在一个临界井深,随着循环时间的升高,临界井深以上的钻柱内流体温度随之增加,而临近井深以下的钻柱内流体温度先降低后升高。
4.3 增压管线排量对井筒温度的影响环空和钻柱循环温度剖面随增压管线排量的变化分别如图 5和图 6所示。
|
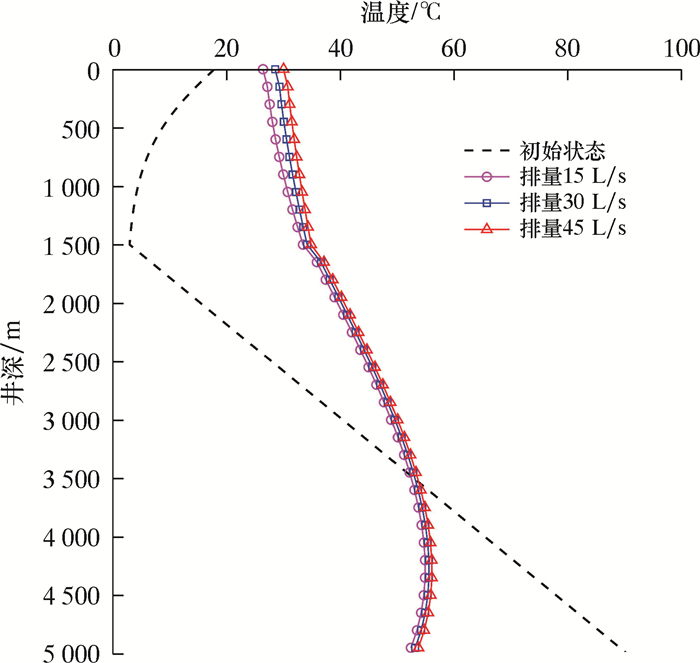
| 图 5 环空循环温度剖面随增压管线排量的变化 Fig.5 Effect of boost line flow rate on annulus circulation temperature profile |
|
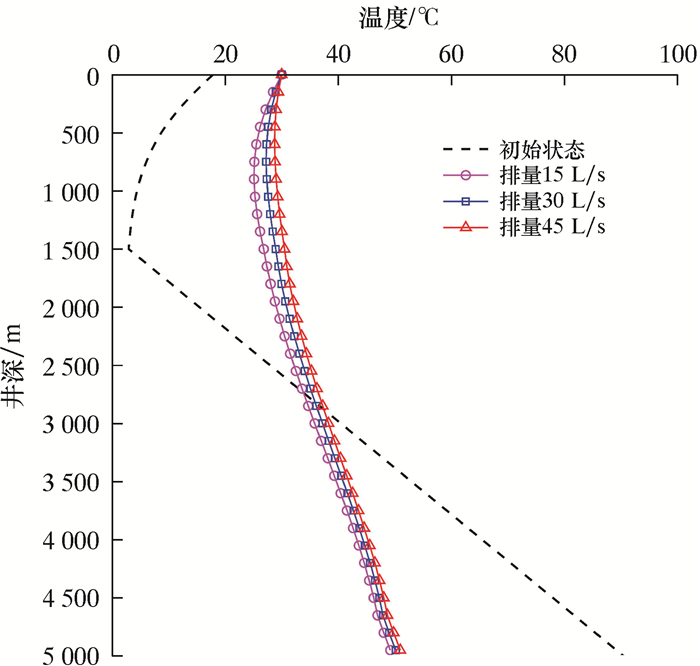
| 图 6 钻柱循环温度剖面随增压管线排量的变化 Fig.6 Effect of boost line flow rate on drill pipe circulation temperature profile |
由图 5可知:增压管线排量仅对海水段的环空温度影响较大,且随着排量的增加,海水段环空温度随之升高;随着距井口距离的减小,增压管线排量对环空温度的影响逐渐增大。
由图 6可知:由于钻柱和环空内流体流动方向相反,增压管线排量对整个钻柱内流体温度的影响较大;随着排量的增加,钻柱内流体温度升高。
4.4 增压管线入口温度对井筒温度的影响环空和钻柱循环温度剖面随入口温度的变化分别如图 7和图 8所示。
|
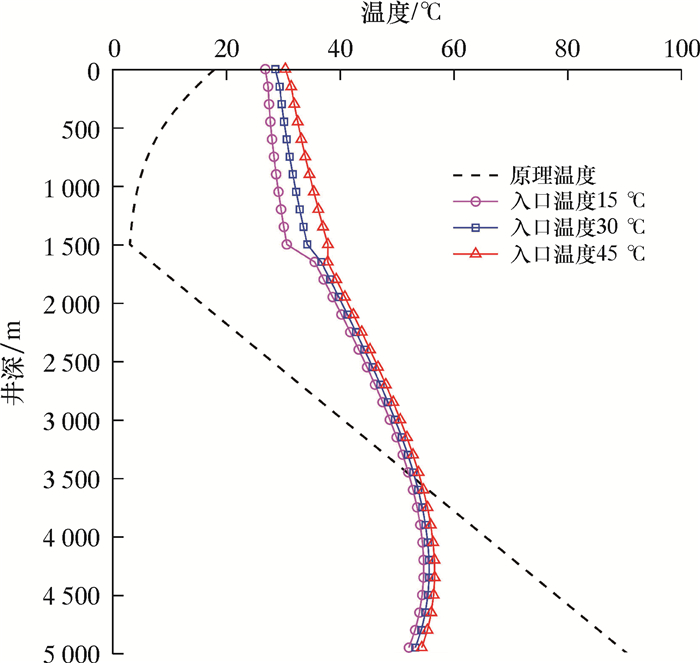
| 图 7 环空循环温度剖面随入口温度的变化 Fig.7 Effect of inlet temperature on annulus circulation temperature profile |
|
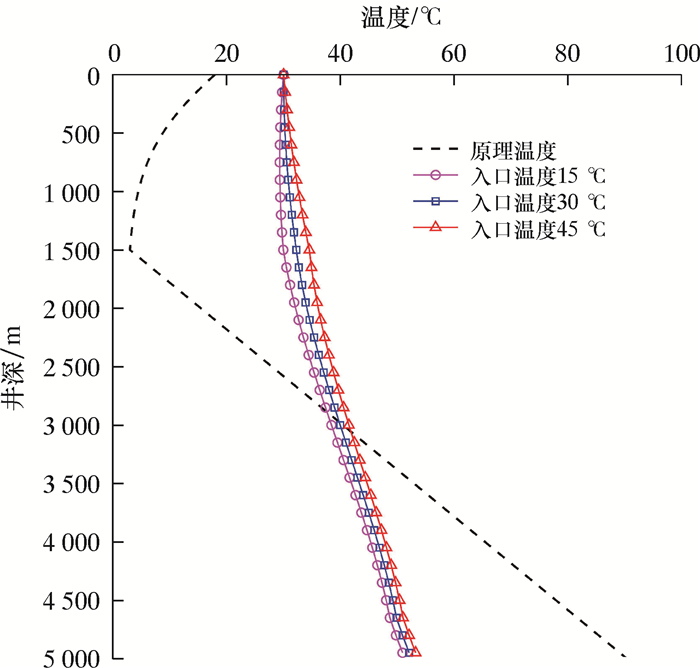
| 图 8 钻柱循环温度剖面随入口温度的变化 Fig.8 Effect of inlet temperature on drill pipe circulation temperature profile |
由图 7可知:增压管线入口温度仅对海水段的环空温度影响较大,且随着入口温度的升高,海水段环空温度随之升高;随着距井口距离的减小,增压管线入口温度对环空温度的影响逐渐减小。
由图 8可知:由于钻柱和环空内流体流动方向相反,增压管线入口温度对整个钻柱内流体温度的影响较大;随着入口温度的升高,钻柱内流体温度随之升高。
5 结论(1) 增压管线排量和入口温度仅对海水段的环空温度影响较大,且随着排量和入口温度的升高,海水段环空温度随之升高。随着距井口距离的减小,增压管线排量对环空温度的影响逐渐增大,而入口温度对环空温度的影响逐渐减小。
(2) 由于钻柱和环空内流体流动方向相反,增压管线排量和入口温度对整个钻柱内流体温度的影响较大,且随着排量和入口温度的升高,钻柱内流体温度随之升高。
| [1] |
王宁, 孙宝江, 王志远. 井筒温度场解析求解的边界条件处理方法[J]. 水动力学研究与进展A辑, 2015(3): 7. WANG N, SUN B J, WANG Z Y. Boundary condition handling for analytic solution of wellbore temperature field[J]. Chinese Journal of Hydrodynamics, 2015(3): 7. |
| [2] |
YANG M, LI X, DENG J, et al. Prediction of wellbore and formation temperatures during circulation and shut-in stages under kick conditions[J]. Energy, 2015, 91: 1018-1029. DOI:10.1016/j.energy.2015.09.001 |
| [3] |
赵金洲, 彭瑀, 李勇明, 等. 基于双层非稳态导热过程的井筒温度场半解析模型[J]. 天然气工业, 2016, 36(1): 68-75. ZHAO J Z, PENG Y, LI Y M, et al. A semi-analytic model of wellbore temperature field based on double-layer unsteady heat conducting process[J]. Natural gas industry, 2016, 36(1): 68-75. |
| [4] |
LI B, LI H, GUO B, et al. A new numerical solution to predict the temperature profile of gas-hydrate-well drilling[J]. SPE Journal, 2017, 22(4): 1201-1212. DOI:10.2118/185177-PA |
| [5] |
YANG M, ZHAO X, MENG Y, et al. Determination of transient temperature distribution inside a wellbore considering drill string assembly and casing program[J]. Applied Thermal Engineering, 2017, 118: 299-314. DOI:10.1016/j.applthermaleng.2017.02.070 |
| [6] |
RAYMOND L R. Temperature distribution in a circulating drilling fluid[J]. Journal of Petroleum Technology, 1969, 21(3): 333-341. DOI:10.2118/2320-PA |
| [7] |
WILLHITE G P. Over-all heat transfer coefficients in steam and hot water injection wells[J]. Journal of Petroleum Technology, 1967, 19(5): 607-615. DOI:10.2118/1449-PA |
| [8] |
ROMERO J, TOUBOUL E. Temperature prediction for deepwater wells: a field validated methodology[R]. SPE 49056, 1998.
|
| [9] |
KARSTAD E, AADNOY B S. Analysis of temperature measurements during drilling[R]. SPE 38603, 1997.
|
| [10] |
宋洵成, 管志川. 深水钻井井筒全瞬态传热特征[J]. 石油学报, 2011, 32(4): 704-708. SONG X C, GUAN Z C. Full transient analysis of heat transfer during drilling fluid circulation in deep-water wells[J]. Acta Petrolei Sinica, 2011, 32(4): 704-708. |
| [11] |
夏环宇, 翟应虎, 安岩, 等. 深水钻井隔水管增压排量对井筒温度分布的影响[J]. 石油钻探技术, 2012, 40(1): 32-36. XIA H Y, ZHAI Y H, AN Y, et al. The effect of boost flow in riser on the wellbore temperature in deep water drilling[J]. Petroleum Drilling Techniques, 2012, 40(1): 32-36. DOI:10.3969/j.issn.1001-0890.2012.01.007 |
| [12] |
陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001. TAO W Q. Numerical heat transfer[M]. Xi'an: Xi'an Jiaotong University Press, 2001. |
| [13] |
SPINDLER R P. Analytical models for wellbore-temperature distribution[J]. SPE Journal, 2011, 16(1): 125-133. DOI:10.2118/140135-PA |
| [14] |
GAO Y, SUN B, XU B, et al. A wellbore/formation-coupled heat-transfer model in deepwater drilling and its application in the prediction of hydrate-reservoir dissociation[J]. SPE Journal, 2017, 22(3): 756-766. DOI:10.2118/184398-PA |



