0 引言
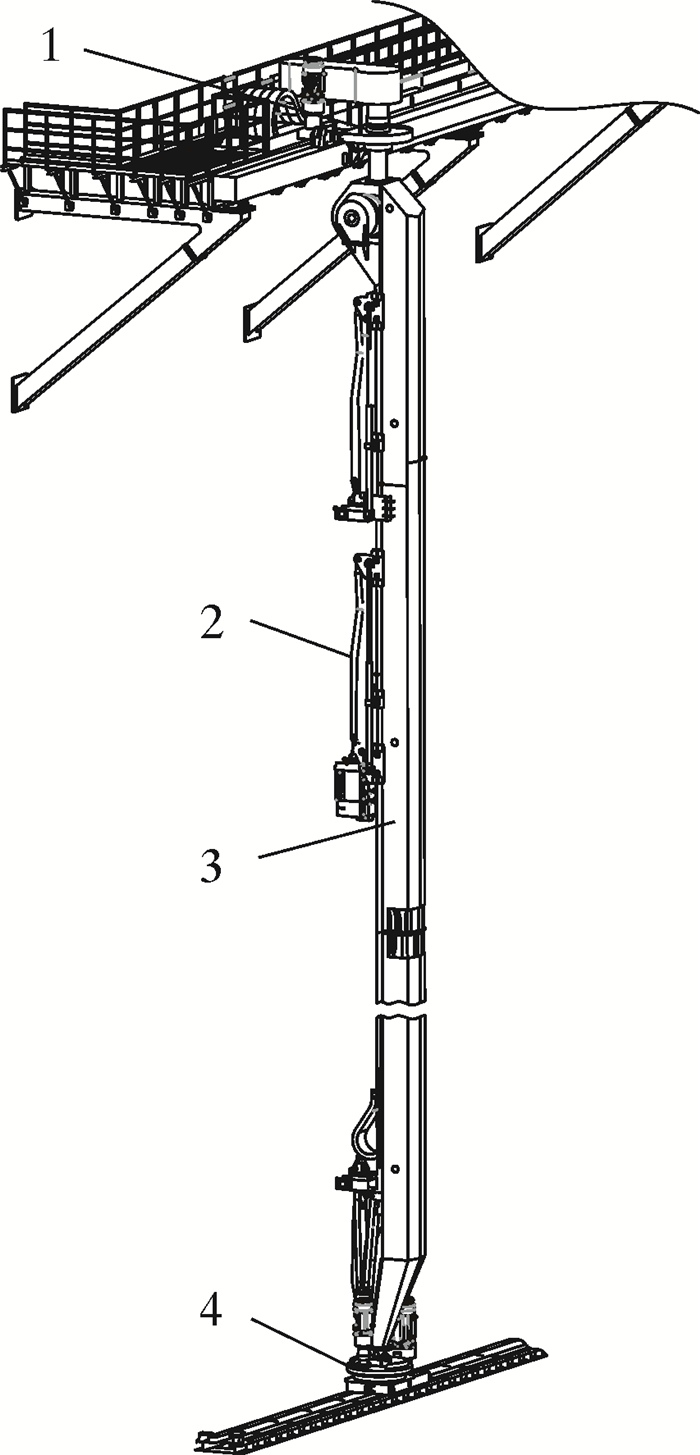
排管机是实现钻井管柱自动化处理的主要设备,通过处理与移运一定管径范围内的钻杆、钻铤及套管,实现三单根立根或四单根立根的接、排、取和甩,大大提高了油气钻探效率。排管机立柱顶端连接上小车,底端连接下小车,通过上、下马达的同步驱动实现立柱和机械臂的水平移动及水平面内回转,同时依靠提升绞车实现主机械臂的竖直移动,进而实现管具在猫道、鼠洞、指梁及井口间的多位置处理。
相较拓扑优化和形状优化而言,尺寸优化是最简单的结构优化方式[1-3],同时尺寸优化更容易快速实现工程结构的降本增效,是设备轻量化设计的重要手段。
笔者以排管机立柱截面尺寸优化为研究重点,利用Design Modeler模块进行参数化建模,利用ANSYS Workbench软件静力学模块对立柱的刚度、强度以及振动模态进行有限元分析。在此基础上,利用Design Explorer模块对各尺寸参数进行敏感性分析和响应面分析,利用响应面法达到减轻质量、增强刚度及提高固有频率的优化目的,实现立柱截面尺寸的快速设计。所得结果可为类似机械设备的尺寸优化设计提供借鉴与参考。
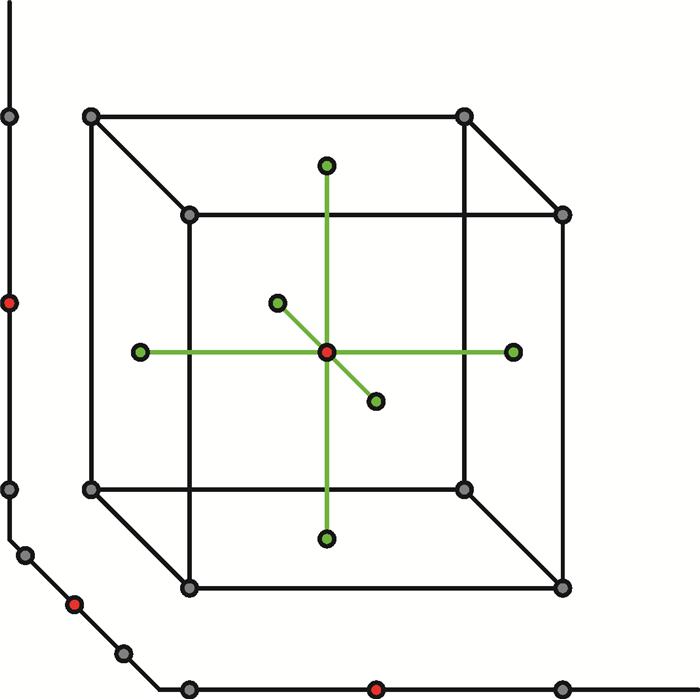
1 理论分析 1.1 中心组合设计法设定自变量的初始值及变化范围变化之后,就确定了试验的样本空间,取样时应选取具有代表性的设计点,以尽可能少的点数最大限度地反映出样本空间数值特点。中心组合设计法(Central Composite Design,CCD)[4-5]是被广泛运用的一种取样方法,该方法中每个自变量(也叫因子)都有5个水平:±β、0及±1,中心点保证了一致精度,轴向距离中心点±β处为极值点,对角线所在轴±1处为析因点。
图 1给出了3因子试验的CCD取样设计点。由图 1可以看出,红色中心点保证了所定义的单位距离的区域内所预测的优化值具有相同的方差,绿色极值点扩展了设计区域,灰色析因点用于估计1阶项和交叉项。
|
| 图 1 3因子试验CCD取样设计点 Fig.1 Three-variable test sampling design points |
为了控制设计点的数量,CCD通过引入析因系数f来剔除部分对角线上的点,这样就能在保证响应面精度的前提下使设计点的数量最少。表 1给出了自变量与设计点数量的关系。
| 自变量(因子)数量n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 析因系数f | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 4 | 5 | 6 | 7 | 8 |
| 设计点数量 | 5 | 9 | 15 | 25 | 27 | 45 | 79 | 81 | 147 | 149 | 151 | 281 | 283 | 285 | 287 | 289 |
1.2 全二阶多项式
响应面法是根据设计点得出的确定性试验结果拟合出一个响应面函数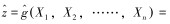
实际工程中的高阶隐式功能函数多采用全二阶多项式(Full 2nd-Order Polynomial)去逼近,其一般形式为:
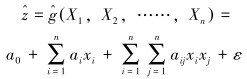
|
(1) |
式中:n为自变量个数,a0、ai、aij为待定系数,ε为随机误差。
从式(1)可以看出,待定系数共有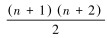
对响应面预测能力的评估,一般采用决定系数R2和均方根差σRMSE两个指标来评价[5]:
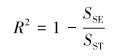
|
(2) |
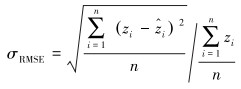
|
(3) |
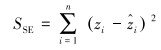
|
(4) |
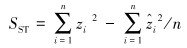
|
(5) |
式中:zi为设计点观测值,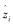
设定样本点数N之后,对于一个n维(自变量数量)问题,非负整数N能够展开成N=a0+a1p+a2p2+……+an-1pn-1,其中p为质数,a∈[0, p-1]。由此构造函数:
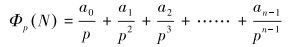
|
(6) |
首先选取质数序列p1<p2<……<pn-1,然后构造Hammersley序列样本点: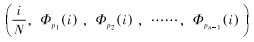
偏移哈默斯利抽样(Shifted Hammersley Sampling,SHS)时将上述样本点整体偏移Δ=N/2,以使它们均匀分布在试验空间中心区域周围,作为多目标优化时遗传算法的初始种群。
2 立柱有限元计算 2.1 立柱截面参数化建模立柱是排管机系统中重要的部件之一,其结构形式如图 2所示。顶端通过关节轴承与上小车连接,底端通过万向节与下小车连接,可以实现水平移动及水平面内回转,此外主机械臂可沿立柱导轨面上下滑移。在方便布置电液管线及传感器的前提下,应尽量增大立柱的抗弯截面模量,考虑到立柱需带有平直导轨面,因此选择五边形作为立柱截面形状。
|
| 1—上小车;2—机械臂;3—立柱;4—下小车。 图 2 排管机系统结构示意图 Fig.2 Structural schematic of the pipe racking system |
Design Modeler模块提供了一个参数化驱动建模方法,通过对称、平行、等长度及等距离等约束命令可以建立如图 3所示的截面。选取6个主要结构尺寸作为自变量:立柱前壁板宽度L1、厚度t1,立柱侧壁板宽度L2、厚度t2、立柱折弯板角度α及厚度t3。6个自变量的初始值分别为:L1=790 mm,L2=580 mm,t1=36 mm,t2=30 mm,t3=30 mm,α=102.7°。
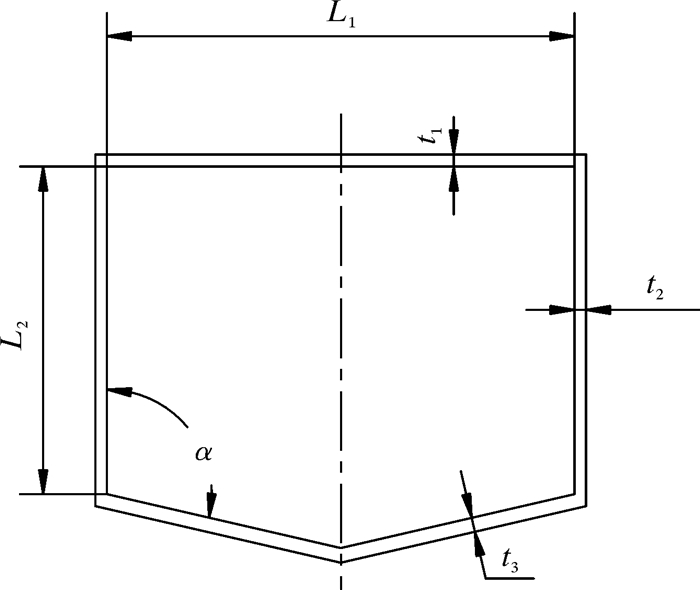
|
| 图 3 立柱截面尺寸 Fig.3 Sectional dimension of the column |
参数化建模的优点在于只改动一个几何自变量时,DM能够在保持其他尺寸、约束不变的前提下自适应生成新的封闭截面,这也为后面的参数敏感性分析奠定了良好的基础。
建立截面尺寸后,采用拉伸方法建出立柱主体,并相继建立立柱的其余零部件。Mechanical模块可以自动生成各零部件之间的“绑定”接触,但需要合理设定Tolerance Value值。
2.2 静力学分析排管机立柱选用Q345E材料。该材料的特性参数[6]如表 2所示。材料特性赋值后,立柱质量为29 370 kg。利用静力学模块对实体单元进行网格划分,网格尺寸应小于50 mm×50 mm[7],对于重点关注的部位应进行网格细化,并确保厚度方向上的网格达到3层以上[8]。图 4和图 5显示了立柱的整体网格及局部细化。
| 公称厚 度/mm |
弹性模量/ GPa |
泊松比 | 材料密度/ (kg·m-3) |
屈服强度/ MPa |
抗拉强度/ MPa |
| ≤16 | 210 | 0.3 | 7 850 | 345 | 470 |
| 16~40 | 210 | 0.3 | 7 850 | 335 | 470 |
| 40~63 | 210 | 0.3 | 7 850 | 325 | 470 |

|
| 图 4 立柱网格划分 Fig.4 Meshing of the column |
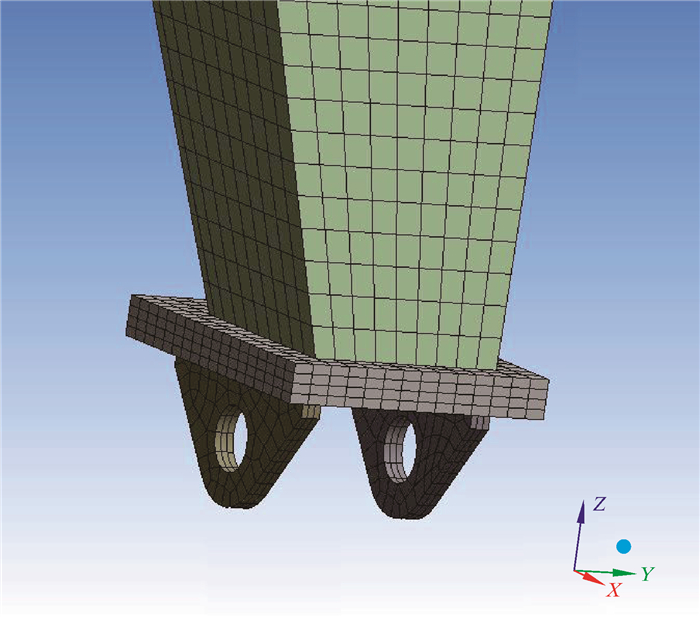
|
| 图 5 立柱耳板网格细化 Fig.5 Mesh refinement of pad eyes on the column |
在考虑硬件运算能力的前提下,划出网格节点380 648个,网格单元54 721个。划出的网格单元质量基本大于0.4,网格偏斜基本小于0.9,网格质量满足使用要求。
该排管机系统用于海洋半潜平台,立柱设计参照提升设备相关要求。美国船级社(ABS)和挪威船级社(DNV)都对提升设备的载荷计算做出了详细的规定[9-10],比较而言,ABS采用1.5°平台静倾角和风浪作用下平台的运动加速度来进行计算,而DNV采用3°平台静倾角和风浪作用下平台的动倾角来计算,本文采用前者做法。
图 6为立柱载荷加载示意图。立柱提升载荷以4根ø241.3 mm(9½ in)钻铤计。动载荷系数VAFonb计算式为[9]:
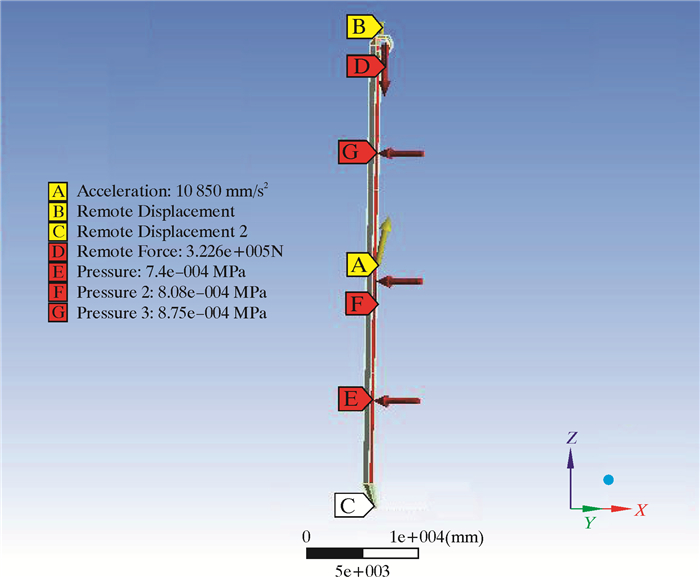
|
| 图 6 立柱载荷加载示意图 Fig.6 Schematic diagram of load on the column |
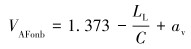
|
(7) |
式中:LL为动载荷,即4立根钻铤的重力,N;av为海洋平台在竖直方向加速度的倍数;C为常数,取值5 220 N。
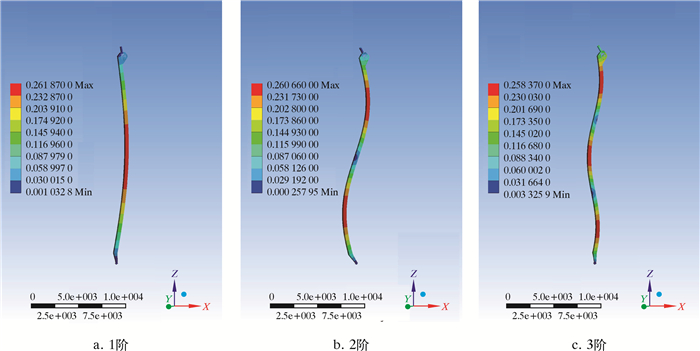
文献[9-10]中给出的风速公式没有考虑高度系数,这对于矗立于井架外侧、长度近40 m的立柱而言显然并不合适。因此风载荷按照公式(8)进行计算[11],并可根据实际情况考虑遮挡系数[12]。
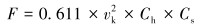
|
(8) |
式中:Cs为形状系数,取1.5;Ch为高度系数,按照立柱距离海平面的高度分段施加;vk为海洋平台10 m高度处的参考风速;F为风载荷。
立柱边界条件选用铰支约束,除分段风压外,立柱还受到提升载荷及3个方向上的惯性加速度。
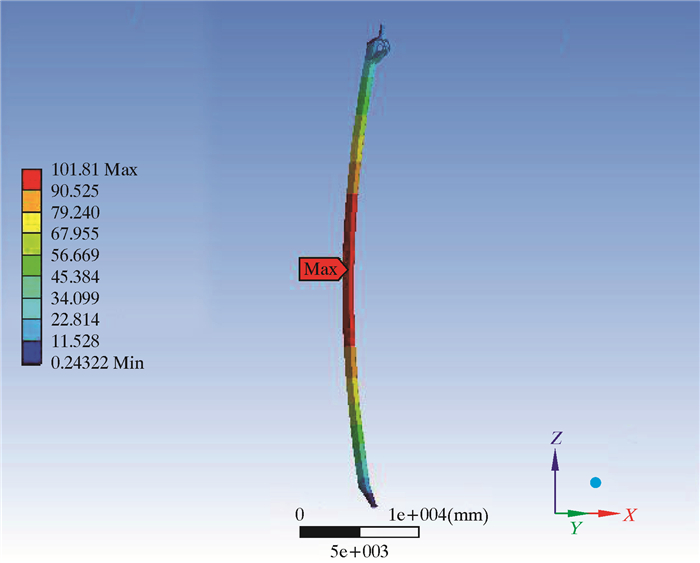
经过有限元计算,立柱的最大总变形为101.81 mm,最大Von Mises等效应力为45.35 MPa。图 7和图 8分别给出了立柱的总变形及等效应力云图。通过强度和刚度分析可知,立柱的应力最大值出现在受弯最严重处并且远小于许用应力值。因此在优化过程中应主要控制立柱的变形。此外,立柱过大的变形也会导致机械臂与指梁之间的定位不准确,进而导致抓管失败。同时,过大的变形也会导致立柱在回转过程中触碰到其他设备。
|
| 图 7 立柱变形云图 Fig.7 Deformation distribution of the column |
|
| 图 8 立柱应力云图 Fig.8 Stress distribution of the column |
2.3 模态分析
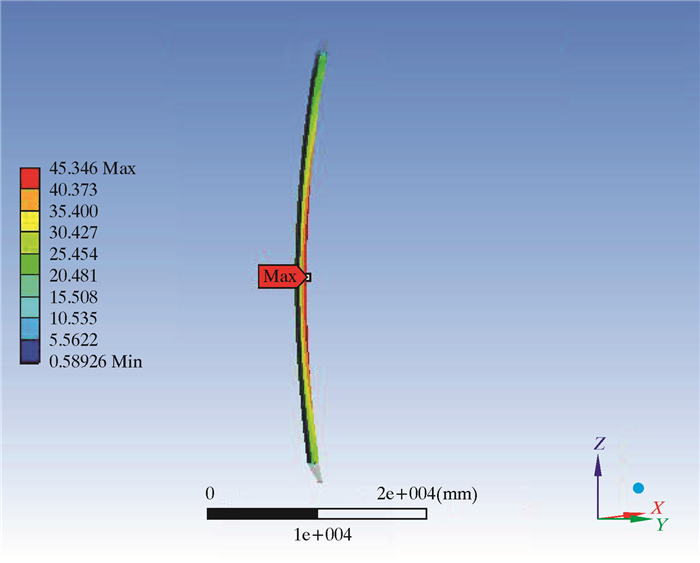
振动模态是立柱的固有特性,只与立柱结构尺寸以及边界条件有关,与外载荷无关。立柱前3阶振型如图 9所示,仅考虑立柱工作平面内的振动,其前3阶振型以正弦函数为主。
|
| 图 9 立柱前3阶振型 Fig.9 The first 3rd order mode shape of the column |
表 3给出了立柱前3阶固有频率。通常情况下,前3阶模态分析结果足以满足设备工作中的振动要求,在优化过程中应提高固有频率,避开外界激励载荷以免发生共振破坏。
| 模态 | 1阶 | 2阶 | 2阶 |
| 固有频率/Hz | 1.337 4 | 5.235 8 | 11.275 0 |
3 参数敏感性及响应面分析
通过敏感性分析,可以得出各自变量参数对目标输出量的影响程度,进而以此为依据有针对性地对某几个自变量进行优化。依据技术指标和设计经验,确定L1、t1、L2、t2、α及t3等6个尺寸参数为自变量,参数变化范围设定为±10%,通过CCD方法在样本空间中构造出45个试验设计点,如表 4所示。
| 设计点 | α/(°) | t1/mm | t2/mm | t3/mm | L1/mm | L2/mm | 总质量/kg | 最大总变形/mm | 最大等效应力/MPa |
| 1 | 102.73 | 36.00 | 580.00 | 30.00 | 790.00 | 30.00 | 29 369.57 | 101.81 | 45.35 |
| 2 | 92.46 | 36.00 | 580.00 | 30.00 | 790.00 | 30.00 | 29 231.54 | 111.20 | 47.04 |
| 3 | 113.00 | 36.00 | 580.00 | 30.00 | 790.00 | 30.00 | 29 771.61 | 91.68 | 44.57 |
| 4 | 102.73 | 32.40 | 580.00 | 30.00 | 790.00 | 30.00 | 28 476.82 | 105.67 | 47.53 |
| 5 | 102.73 | 39.60 | 580.00 | 30.00 | 790.00 | 30.00 | 30 257.93 | 98.40 | 43.43 |
| 6 | 102.73 | 36.00 | 522.00 | 30.00 | 790.00 | 30.00 | 28 348.02 | 119.85 | 56.15 |
| 7 | 102.73 | 36.00 | 638.00 | 30.00 | 790.00 | 30.00 | 30 386.05 | 88.24 | 43.08 |
| 8 | 102.73 | 36.00 | 580.00 | 27.00 | 790.00 | 30.00 | 28 606.29 | 104.99 | 45.20 |
| 9 | 102.73 | 36.00 | 580.00 | 33.00 | 790.00 | 30.00 | 30 128.45 | 99.12 | 45.51 |
| 10 | 102.73 | 36.00 | 580.00 | 30.00 | 711.00 | 30.00 | 27 825.46 | 107.60 | 64.34 |
| 11 | 102.73 | 36.00 | 580.00 | 30.00 | 869.00 | 30.00 | 30 909.37 | 96.99 | 43.38 |
| 12 | 102.73 | 36.00 | 580.00 | 30.00 | 790.00 | 27.00 | 28 248.90 | 101.76 | 45.64 |
| 13 | 102.73 | 36.00 | 580.00 | 30.00 | 790.00 | 33.00 | 30 484.66 | 101.87 | 45.09 |
| 14 | 96.79 | 33.92 | 546.47 | 28.27 | 744.34 | 28.27 | 26 278.84 | 127.14 | 66.67 |
| 15 | 108.67 | 33.92 | 546.47 | 28.27 | 744.34 | 31.73 | 27 762.67 | 112.83 | 48.01 |
| 16 | 96.79 | 38.08 | 546.47 | 28.27 | 744.34 | 31.73 | 28 479.50 | 120.99 | 62.00 |
| 17 | 108.67 | 38.08 | 546.47 | 28.27 | 744.34 | 28.27 | 27 520.88 | 108.24 | 46.05 |
| 18 | 96.79 | 33.92 | 613.53 | 28.27 | 744.34 | 31.73 | 28 746.44 | 104.55 | 47.10 |
| 19 | 108.67 | 33.92 | 613.53 | 28.27 | 744.34 | 28.27 | 27 660.84 | 95.13 | 45.64 |
| 20 | 96.79 | 38.08 | 613.53 | 28.27 | 744.34 | 28.27 | 28 358.77 | 100.54 | 45.06 |
| 21 | 108.67 | 38.08 | 613.53 | 28.27 | 744.34 | 31.73 | 29 986.40 | 91.50 | 43.11 |
| 22 | 96.79 | 33.92 | 546.47 | 31.73 | 744.34 | 31.73 | 28 322.48 | 122.14 | 62.46 |
| 23 | 108.67 | 33.92 | 546.47 | 31.73 | 744.34 | 28.27 | 27 404.41 | 108.97 | 48.69 |
| 24 | 96.79 | 38.08 | 546.47 | 31.73 | 744.34 | 28.27 | 28 063.16 | 117.95 | 66.71 |
| 25 | 108.67 | 38.08 | 546.47 | 31.73 | 744.34 | 31.73 | 29 601.97 | 104.62 | 45.88 |
| 26 | 96.79 | 33.92 | 613.53 | 31.73 | 744.34 | 28.27 | 28 203.11 | 101.64 | 47.65 |
| 27 | 108.67 | 33.92 | 613.53 | 31.73 | 744.34 | 31.73 | 29 868.92 | 92.11 | 45.38 |
| 28 | 96.79 | 38.08 | 613.53 | 31.73 | 744.34 | 31.73 | 30 546.22 | 97.35 | 44.91 |
| 29 | 108.67 | 38.08 | 613.53 | 31.73 | 744.34 | 28.27 | 29 484.34 | 88.48 | 43.56 |
| 30 | 96.79 | 33.92 | 546.47 | 28.27 | 835.66 | 31.73 | 29 166.59 | 119.73 | 66.29 |
| 31 | 108.67 | 33.92 | 546.47 | 28.27 | 835.66 | 28.27 | 28 253.76 | 105.21 | 45.77 |
| 32 | 96.79 | 38.08 | 546.47 | 28.27 | 835.66 | 28.27 | 29 024.97 | 114.80 | 66.55 |
| 33 | 108.67 | 38.08 | 546.47 | 28.27 | 835.66 | 31.73 | 30 554.59 | 101.31 | 43.02 |
| 34 | 96.79 | 33.92 | 613.53 | 28.27 | 835.66 | 28.27 | 29 055.04 | 99.39 | 45.08 |
| 35 | 108.67 | 33.92 | 613.53 | 28.27 | 835.66 | 31.73 | 30 711.65 | 89.25 | 42.77 |
| 36 | 96.79 | 38.08 | 613.53 | 28.27 | 835.66 | 31.73 | 31 501.74 | 95.39 | 42.52 |
| 37 | 108.67 | 38.08 | 613.53 | 28.27 | 835.66 | 28.27 | 30 445.12 | 85.65 | 40.95 |
| 38 | 96.79 | 33.92 | 546.47 | 31.73 | 835.66 | 28.27 | 28 851.51 | 115.89 | 58.57 |
| 39 | 108.67 | 33.92 | 546.47 | 31.73 | 835.66 | 31.73 | 30 423.78 | 101.81 | 45.64 |
| 40 | 96.79 | 38.08 | 546.47 | 31.73 | 835.66 | 31.73 | 31 169.88 | 111.05 | 61.89 |
| 41 | 108.67 | 38.08 | 546.47 | 31.73 | 835.66 | 28.27 | 30 285.25 | 97.47 | 43.62 |
| 42 | 96.79 | 33.92 | 613.53 | 31.73 | 835.66 | 31.73 | 31 326.94 | 96.35 | 44.97 |
| 43 | 108.67 | 33.92 | 613.53 | 31.73 | 835.66 | 28.27 | 30 315.32 | 86.26 | 43.33 |
| 44 | 96.79 | 38.08 | 613.53 | 31.73 | 835.66 | 28.27 | 31 042.87 | 92.39 | 42.96 |
| 45 | 108.67 | 38.08 | 613.53 | 31.73 | 835.66 | 31.73 | 32 758.94 | 83.01 | 40.87 |
图 10给出了全局敏感性分析结果。由图 10可知:6个自变量对输出变量的影响各不相同,自变量对质量的影响都是正相关,L1对质量的敏感度最大,其次是t2、L2和t3;L2和α对最大总变形的敏感度最高,敏感性系数为负值说明自变量增大,最大总变形会减小,这也是立柱优化时最关心的问题;L2、α、L1及t1对最大等效应力的敏感度都是负相关。
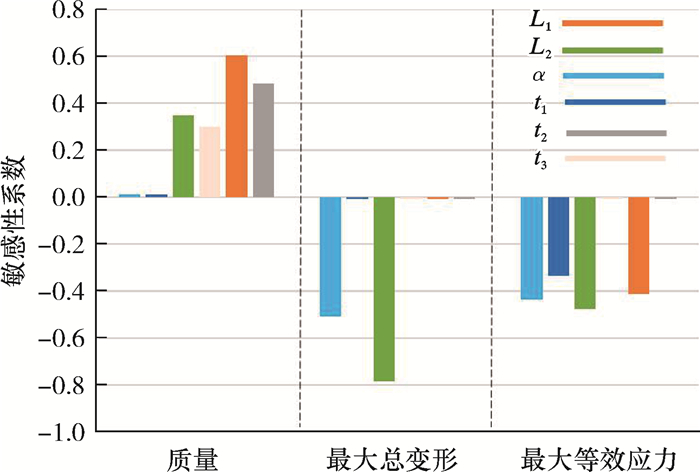
|
| 图 10 全局敏感性分析 Fig.10 Global sensitivity analysis |
通过图 11所示的局部敏感性分析结果,可快速查看各尺寸参数对最大等效应力的敏感趋势。各条敏感性曲线都汇交于响应点,在该点处各自变量对最大等效应力的敏感度均一致。图 11中有关t2的曲线与t3的曲线重合了。
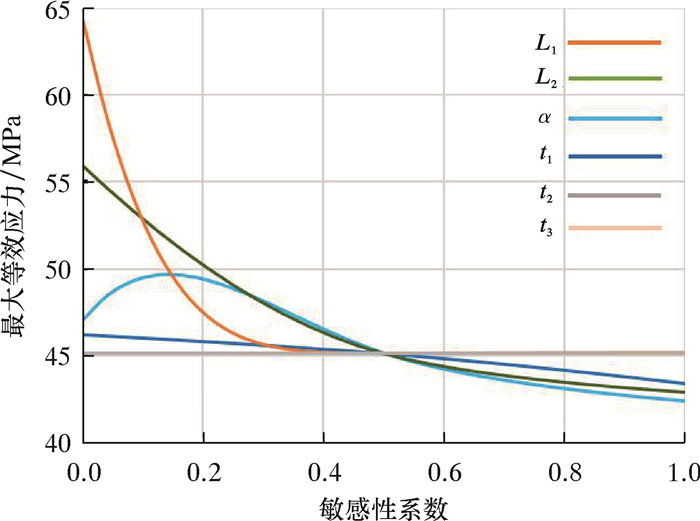
|
| 图 11 局部敏感性分析 Fig.11 Local sensitivity analysis |
Design Explorer模块利用全二阶多项式去拟合出响应面函数。图 12给出了拟合度符合性分布图。通过表 5的拟合度评价值可以看出拟合出的响应面结果可信。
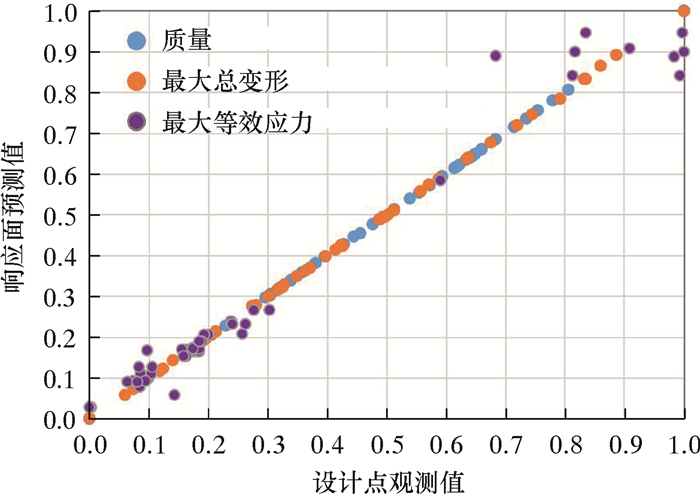
|
| 图 12 拟合度符合性分布图 Fig.12 Fit degree conformity |
| 项目 | 决定系数R2 | 均方根差σRMSE |
| 质量 | 0.999 999 998 | 0.000 041 373 1 |
| 最大总变形量 | 0.999 999 174 | 0.000 903 353 0 |
| 最大等效应力 | 0.999 195 053 | 0.028 425 244 0 |
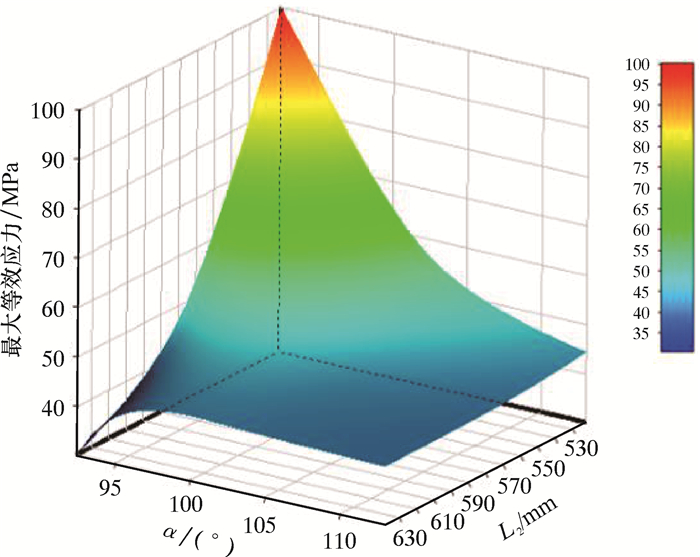
结合敏感性分析结果,重点关注L2和α对最大总变形量以及最大等效应力的响应曲面。图 13所示为最大总变形量响应面。从图 13可以看出,L2和α对最大变形量的影响是线性负相关,增大L2和α的数值可以有效减小最大总变形量。图 14所示的响应面结果表明,L2和α对最大等效应力的影响是非线性的,随着α的增大,最大等效应力先升高后降低,L2增大时最大等效应力会减小。
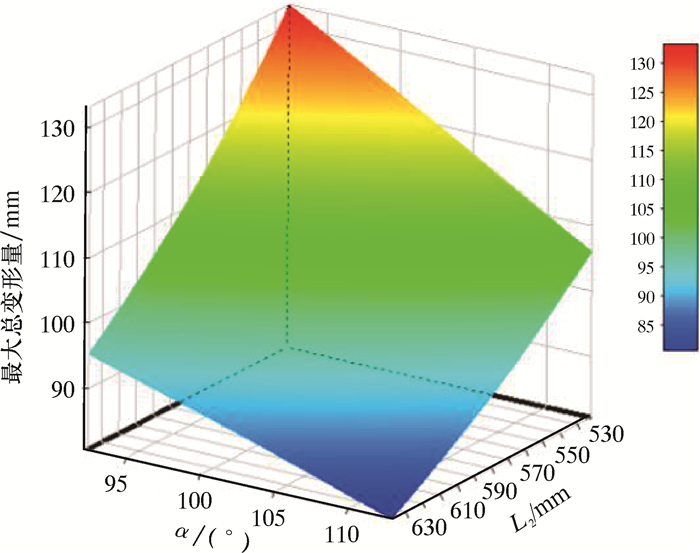
|
| 图 13 最大总变形量响应面 Fig.13 Maximum total deformation response surface |
|
| 图 14 最大等效应力响应面 Fig.14 Maximum equivalent stress response surface |
4 响应曲面优化分析
尺寸优化分析往往会涉及多目标期望,而且多个目标期望之间可能存在矛盾,比如立柱截面板厚越厚,结构的变形就越小,但结构质量就会增大,因此多目标优化时就要找出各个互相对立问题的最佳平衡点。对于排管机立柱而言,应找到一组最合适的结构参数自变量,尽可能达到质量轻、成本低,满足强度和刚度要求,即有:
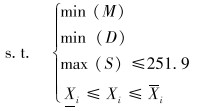
|
(9) |
式中:M为立柱几何质量,D为立柱最大总变形量,S为立柱最大等效应力,Xi为参数自变量,即为L1、L2、t1、t2、t3和α,Xi为结构尺寸自变量下限值,Xi为结构尺寸自变量上限值。
利用SHS方法得到样本点后作为遗传算法的初始种群,计算群体中个体对目标变量数学期望值的适用度,将优化的个体直接遗传到下一代或者配对交叉后遗传到下一代,通过与目标期望值的不断比较给出优化解。表 6给出了3组解集。从前面章节的分析结果可知,立柱优化过程中主要考虑控制其最大总变形量,因此选择第2组优化方案,圆整后L1=780 mm,L2=634 mm,t1=33 mm,t2=27 mm,t3=29 mm,α=109.6°。此时立柱的整体质量为28 562 kg,减轻934.3 kg,相较原方案质量减轻3.2%;总体变形量降低14.1%,最大等效应力也有所降低,提高了结构强度。
| 参数 | 方案1 | 方案2 | 方案3 | 原方案 |
| α/(°) | 111.739 | 109.644 | 103.542 | 102.700 |
| t1 /mm | 34.815 | 33.381 | 38.486 | 36.000 |
| L2 /mm | 610.424 | 634.292 | 635.512 | 580.000 |
| t3 /mm | 31.200 | 28.839 | 32.369 | 30.000 |
| L1 /mm | 716.738 | 780.307 | 712.987 | 790.000 |
| t2 /mm | 29.068 | 27.526 | 27.269 | 30.000 |
| 质量/kg | 28 443.32 | 28 435.73 | 28 850.30 | 29 370.00 |
| 最大总变形量/mm | 91.958 | 87.425 | 89.070 | 101.810 |
| 最大等效应力/MPa | 57.240 | 43.134 | 59.808 | 45.350 |
表 7为优化后工作平面内前3阶固有频率。由表 7可知,优化方案中一阶固有频率提高9.4%,二阶固有频率提高8.8%,三阶固有频率提高7.7%,均有效提高了设备工作性能。
| 模态 | 1阶 | 2阶 | 3阶 |
| 固有频率/Hz | 1.475 9 | 5.743 5 | 12.219 0 |
从以上结果可以看出,新方案达到了减轻立柱质量、增强刚度及提高固有频率的优化目的。
5 结论(1) 系统总结了海洋平台用排管机立柱有限元计算时应遵循的方法与规范。工作载荷应按照ABS或DNV对提升设备的设计要求进行加载并考虑动载系数,风载荷应考虑高度系数;实体单元网格划分时尺寸应小于50 mm×50 mm,关键部位应划分3层以上网格,整体网格指标中单元质量应大于0.4,偏斜应小于0.9。
(2) 通过参数敏感性分析和响应面分析发现,立柱侧壁板宽度L2和折弯板角度α对最大总变形的敏感度最高,增大L2和α的数值可以有效减小最大总变形量;L2和α对最大等效应力的影响是非线性的,随着α的增大最大等效应力先升高后降低,L2增大时最大等效应力会降低。
(3) 利用响应面法得到优化方案,相较原方案质量减轻3.2%,最大总变形量降低14.1%,最大等效应力降低的同时前3阶固有频率均有所提高,达到了减轻立柱质量、增强刚度及提高固有频率的优化目的,实现了立柱截面尺寸的快速优化设计。
| [1] |
刘承杰, 罗鹏, 赵磊, 等. 基于ANSYS Workbench曲柄销轴的优化设计[J]. 应用力学学报, 2017, 34(6): 1140-1144. LIU C J, LUO P, ZHAO L, et al. Optimal design of crank pin based on ANSYS Workbench[J]. Chinese Journal of Applied Mechanics, 2017, 34(6): 1140-1144. |
| [2] |
姚道壮, 杨建国, 吕志军. 基于ANSYS Workbench的货架立柱截面优化设计[J]. 东华大学学报(自然科学版), 2011, 37(4): 438-441, 475. YAO D Z, YANG J G, LÜ Z J, et al. Optimization of steel storage rack column cross-sections based on ANSYS Workbench[J]. Journal of Donghua University (Natural Science), 2011, 37(4): 438-441, 475. DOI:10.3969/j.issn.1671-0444.2011.04.012 |
| [3] |
艾延廷, 路闯, 武威, 等. 螺栓连接纵向安装边机匣的有限元分析与优化[J]. 科学技术与工程, 2013, 13(29): 8684-8690. AI Y T, LU C, WU W, et al. Bolt connection with the longitudinal edge of casing installation finite element analysis and optimization[J]. Science Technology and Engineering, 2013, 13(29): 8684-8690. DOI:10.3969/j.issn.1671-1815.2013.29.026 |
| [4] |
张志红, 何桢, 郭伟. 在响应曲面方法中三类中心复合设计的比较研究[J]. 沈阳航空工业学院学报, 2007, 24(1): 87-91. ZHANG Z H, HE Z, GUO W. A comparative study of three central composite designs in response surface methodology[J]. Journal of Shenyang Institute of Aeronautical Engineering, 2007, 24(1): 87-91. DOI:10.3969/j.issn.2095-1248.2007.01.026 |
| [5] |
姜衡, 管贻生, 邱志成, 等. 基于响应面法的立式加工中心动静态多目标优化[J]. 机械工程学报, 2011, 47(11): 125-133. JIANG H, GUAN Y S, QIU Z C, et al. Dynamic and static multi-objective optimization of a vertical machining center based on response surface method[J]. Journal of Mechanical Engineering, 2011, 47(11): 125-133. |
| [6] |
全国钢标准化技术委员会.低合金高强度结构钢: GB/T 1591-2008[S].北京: 中国标准出版社, 2008. National Technical Committee on Steel of Standardization Administration of China. High strength low alloy structural steels: GB/T 1591-2008[S]. Beijing: Standards Press of China, 2008. |
| [7] |
中国船级社.海上移动平台入级规范[S].北京: 人民交通出版社, 2012. China Classification Society. Rules for classification of mobile offshore units[S]. Beijing: China Communications Press, 2012. |
| [8] |
中国国家标准化管理委员会.机械产品结构有限元力学分析通用规则: GB/T 33582-2017[S].北京: 中国标准出版社, 2017. National Technical Committee on Steel of Standardization Administration of China. General principles of structuralfinite element analysis for mechanical products: GB/T 33582-2017[S]. Beijing: Standards Press of China, 2017. |
| [9] |
American Bureau of Shipping.Guide for certification of lifting appliances[EB/OL].(2018-08-27).http://www.eagle.org/.
|
| [10] |
Det Norske Veritas. Lifting appliances (2013): No.2.22[EB/OL].[2018-08-27]. http://www.dnvgl.com.
|
| [11] |
American Bureau of Shipping. Rules for building and classing mobile offshore drilling units: 2012[EB/OL].[2018-08-27]. http://www.eagle.org/.
|
| [12] |
American Petroleum Institute. Specification for drilling and well servicing structures[S]. Washington: API Publishing Services, 2008.
|


