0 引言
近年来,聚晶金刚石复合片(PDC)钻头以其广泛的地层适应性、自锐性,以及成本低廉等特点[1-2],占据了油气开采行业70%以上的市场。结合我国当前阶段,《国土资源“十三五”科技创新发展规划》中,我国将以深地、深海、深空为主攻方向和突破口,构建“三深一土”的国土资源战略科技新格局的目标,目前运用PDC钻头高效合理开发油气和地质资源已经成为主流趋势。
为提高PDC钻头的钻进效率,国内外众多研究人员在PDC钻头的破岩机理方面进行了研究工作,大多数研究通过试验或模拟在单齿切削过程中进行。W.J.LIU等[3]用离散元模型分析了刀具的破岩过程,发现应力变化与能量累积有关。B.AKBARI等[4]通过单齿切削试验研究了岩石的破坏机理,发现单齿切削试验可以更好地观察与分析PDC刀具与岩石表面接触情况。由于PCD(聚晶金刚石层)材料在切削过程中容易发生脆性断裂、高温下降解以及切削技术本身的限制,这些研究都基于低速切削条件进行。随着PCD加工过程中优化了颗粒尺寸选择和粘合剂,材料性质得到了极大提升[5],并且随着切削领域高速切削技术的进步,已经具备将高转速及其转化而成的高线速度应用到PDC刀具破岩的可行性。
早在20世纪20年代, 德国学者Salomon发现,当切削速度达到一定值后,一些工件材料的切削力和切削温度不再上升, 反而下降[6]。随着高速切削刀具与机床设备取得突破性的进展,这个发现在硬材料的切削试验中得到了证明。其中,铝合金的高速切削速度已经达到1 500~5 500 m/min,铸铁的高速切削速度也达到了750~4 500 m/min[7]。根据高速切削在这些领域的应用,部分研究者开始将高速钻进作为优化钻进参数的一个突破点。早在2002年美国能源部就开始了相关的研究,TerraTek实验室发现,通过应用高转速(大于10 000 r/min),深钻硬岩钻探将实现重大突破,研究发现,高转速条件下可以实现高效岩石切削,同时能量和钻压相对于常规钻井工程而言出现大幅度降低趋势。这证明了高速切削破岩的可行性,但是目前世界各国尚未有针对PDC刀具高速切削破岩机理方面的研究。
为了研究PDC刀具高速切削破岩机理,本工作通过ABAQUS软件构建PDC刀具线性切削岩石模型,模拟高速条件下PDC刀具的切削试验。从温升、应力、能量变化及切屑形成机制4个方面探究高速条件下PDC刀具的切削机理。
1 高速切削模型的数值模拟 1.1 高速切削模型图 1a为ABAQUS高速切削模型示意图。其中刀具直径为6 mm,刀具厚度为2 mm,摩擦因数为0.1,切削速度v分别为0.5、5.0、10.0、15.0和20.0 m/s,进尺度为2.5 mm,切削时间为0.03 s,后倾角为-10°。刀具前刀面材料设置为PCD(聚晶金刚石层),下部为碳化钨合金。为满足高精度模拟岩石破坏并且尽量提高运算速度的要求,岩石上部与刀具前端面局部网格加密,其余部分网格稀疏。网格划分如图 1b所示。在边界条件方面,岩石底面和左侧面施加固定约束,由于模型不考虑围压和边界固定条件对岩石破碎过程的影响,切削部分不能超过总长度的1/3,所以根据计算岩石模型总长度设计为1 m。

|
| 图 1 ABAQUS高速切削模型与网格划分 Fig.1 ABAQUS high-speed cutting model and mesh generation |
1.2 材料模型
ABAQUS中存在Drucker-Prager和Ductile-Damage连续作用的塑性和损伤2种模型。由于常规刀具切削岩石过程实质上是以压力为主导和切削力共同作用的,笔者选用可以更好表征与压力相关的各个量的Drucker-Prager塑性模型。在塑性损伤准则中,损伤起始时的等效塑性应变是应变率和应力三轴η的函数,它是平均应力与Von-Mises应力的比值[8],即有:
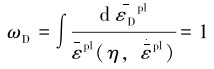
|
(1) |
式中:εpl是损伤开始时的等效塑性应变,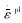
一旦切削损伤开始,刚度就会降低,这可以通过损伤演化规律计算出来。在ABAQUS中,损伤演化受下式控制:
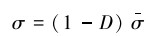
|
(2) |
式中:D是损伤变量,σ是任何时间的应力张量,σ是未受损的应力张量。
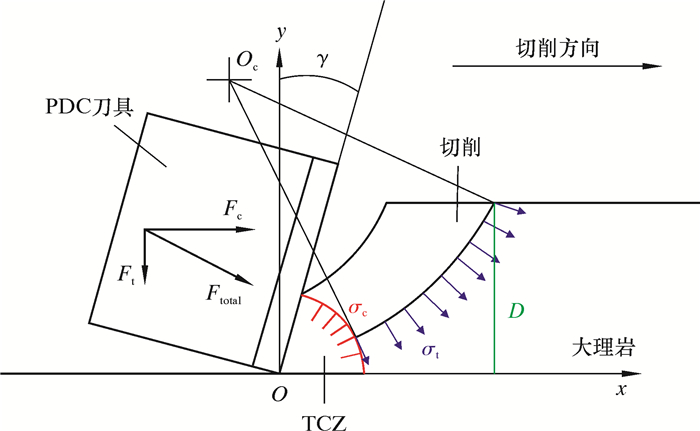
1.3 切削理论模型高速切削机理如图 2所示。图中红色和阴影区域为岩石破碎区,即顶端破碎区(TCZ)形成在刀具前刀面下方且靠近刀刃位置。由于TCZ是岩石破碎形成的,所以从物理角度来看,TCZ边界被假定为具有与岩石的单轴抗压强度σc相等的均匀应力分布的弧。在切削过程中,TCZ沿着切削速度方向进一步移动,并在刀具前刀面下方连续形成一个稳定的破碎区域[9]。
|
| 图 2 高速切削机理示意图 Fig.2 Schematic diagram of high-speed cutting mechanism |
由于高速切削加工迅速形成切屑,所以在将切屑从未变形的岩石分离之前沿着弧形裂纹传播路径的应力分布假定为均匀的,其值等于岩石的拉伸强度应力σt,如图 2所示[10]。
1.4 评价指标根据上述切削模型,笔者将通过切屑大小及形成机理、温升情况、应力变化和表征切削效率的PMSE(机械比能)4个方面对数值模拟结果进行分析。PMSE通常是作为在全PDC钻头的切削效率的评价指标。由于上述模型中刀具的初始制动之外,其中一个根本区别是在垂直方向上没有相对运动。系统中唯一力是切削力,因此单齿模型中的PMSE可以简化为以下等式[4]:
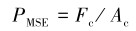
|
(3) |
式中:Fc是切削力,Ac是截面积。
2 试验结果与讨论 2.1 PDC高速切削对切屑形成机理的影响在传统切削机理分析中,切屑的大小形状是研究切削机理的重要组成部分。在常规切削中,刀具与岩石切削面相对平滑,切削过程主要是压碎作用。在刀尖周围形成高应力区和塑性区,裂纹从塑性区开始向自由表面延伸,最终形成切屑。
图 3显示了2种切削速度下岩石的破坏与切屑的形成过程。如图 3a所示,在PDC刀具破碎作用下,岩石部分的形状和尺寸明显变化,表现为塑性破坏,没有大的切屑产生。图 3b中破坏形式表现为脆性破坏,切削时没有明显的形状变化,刀具与岩石切削面凹凸不平。通过比较可以发现,岩石在高速切削条件下更容易发生脆性破坏,进而产生大切屑。

|
| 图 3 不同切削速度条件下切屑形态 Fig.3 Cuttings at different cutting speeds |
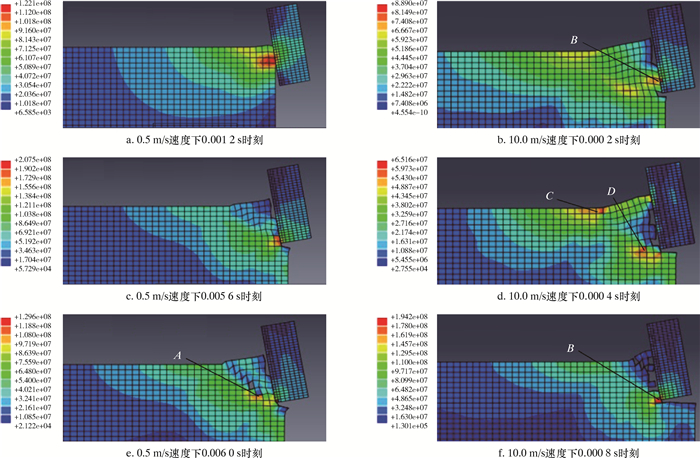
高速与低速切削条件下第一个切削周期切屑逸散过程如图 4所示。0.5 m/s的切削速度条件下,切屑形成过程从应力角度分析可以分为3个阶段,图 4a为刀具与岩石接触的第1阶段,岩石表面出现变形,在刀具与岩石接触部位附近的岩石上出现明显的应力集中。图 4c在第2阶段中,前一阶段岩石变形与刀具接触的部分被破坏,该部分应力得到释放,应力在新的刀具与岩石接触部分开始集中。如图 4e,在第3阶段中,岩石变形部分与未变形部分开始分离,应力释放,切屑的形成可能是A(刀具与岩石接触点附近)点位置集中的应力主导的。至此,在0.004 8 s内完成1次岩石破坏、切屑形成的周期,此时切削下端面非常平滑。
|
| 图 4 高速与低速切削条件下第1个切削周期切屑逸散过程示意图 Fig.4 Schematic diagram of cutting dispersion process in the first cutting cycle under high speed and low speed cutting conditions |
在高速切削条件下,切屑形成过程可以分为3个阶段。这个结果也可以用图 2高速切削机理示意图解释。第1阶段如图 4b所示,刀具切削岩石形成微切屑,应力集中区域分布在B点(刀具与岩石接触点下部)并主导TCZ成为切削岩石过程中最先碎裂的部分。第2阶段如图 4d所示,岩石严重变形,应力集中在C点(岩石变形与未变形连接区域)和D点(刀具与岩石接触点下部的岩石内部),裂纹在TCZ边界上开始并沿着弧形路径向原始岩石的自由表面传播,并且形成微切屑。第3阶段如图 4f所示,应力集中在B、C和D处,其中B点位置的应力明显大于C、D处使得裂纹扩展,切屑由沿着岩石变形区域和原始岩石之间的裂缝传播路径的拉应力而形成。这个切屑形成周期为0.000 6 s,并且说明大切屑是由B点切削力主导,C、D点的应力共同作用的结果。
对比常规速度切削与高速切削过程,发现以压碎作用为主的塑性破岩方式开始转化为以切削作用为主的脆性破坏形式,在这个阶段下切削力更加稳定,能量积累时间更短,更利于破碎岩石。因此,从切屑角度分析,适宜的高速切削具体速度应该超过5.0 m/s。
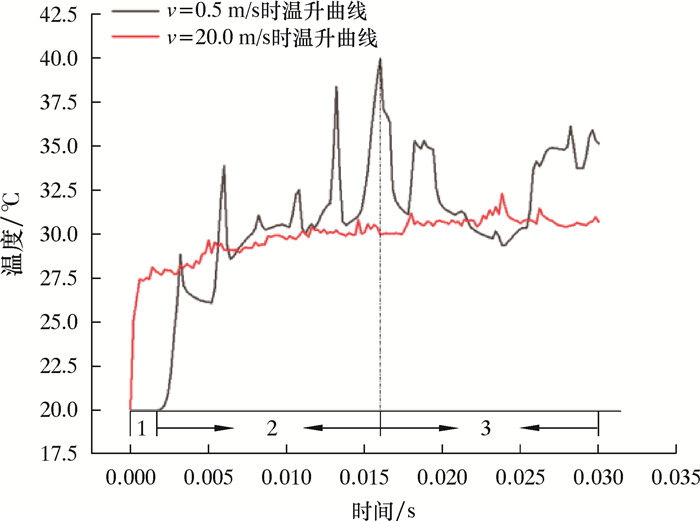
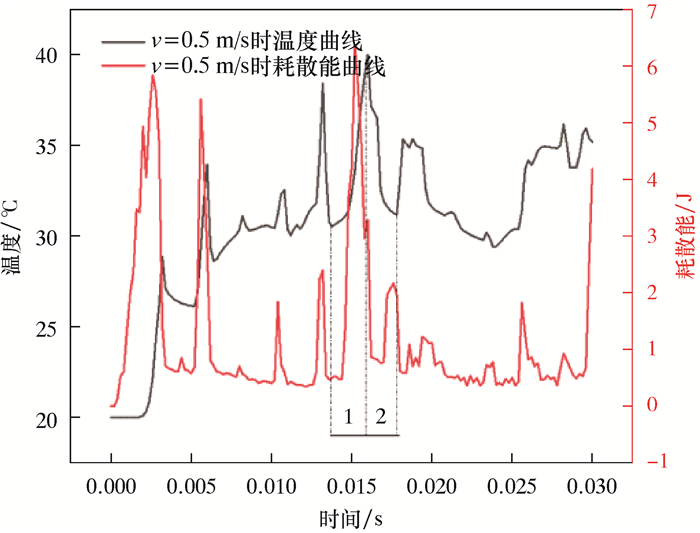
2.2 高速切削对PDC刀具表面温度的影响高速与低速切削条件下温升曲线对比如图 5所示。由图 5可以看出,在常规切削速度为0.5 m/s时,温升曲线明显存在3个阶段。阶段1为0.000~0.002 s,刀具还未接触到岩石表面,其表面保持室温。阶段2为0.002~0.016 s,刀具与岩石接触产生大量的热,最高温超过40 ℃。阶段3为0.016~0.030 s,刀具表面温度出现周期性波动,这可能是刀具切削岩石过程中,切屑周期性逸散带走部分热量导致的。另一方面,温升曲线与耗散能曲线基本保持同步(见图 6),这是由于切削速率低,刀具前端面需要一定时间的能量累积以到达破岩的临界能量,在这个过程中温度迅速提高,当累积能量超过破岩临界能量后,刀具破碎岩石,刀具前端面温度迅速下降。在切削温度大幅度变化的一个周期内,刀具前端面的温升曲线分为以下2个阶段,在图 6的第1阶段中,在刀具压入岩石,此时岩石尚未破碎,刀具前端面与岩石表面摩擦产生大量的热,热量迅速累积,局部区域产生的高变形使得热量传导不畅,最终刀具前刀面迅速升温;在第2阶段中,热量稳定累积,刀具切削速率快,累积热量时间短,并且快速破碎的切屑迅速带走热量,热量逸散快,温度从高点回落,但是总体呈现热能逐渐累积。因此总体而言在高速切削条件下,刀具表面的温度远低于常规切削速度下刀具表面温度,这个结果也验证了德国学者Salomon的观点[4]。
|
| 图 5 高速与低速切削条件下温升曲线对比图 Fig.5 Comparison of temperature rise curves under high speed and low speed cutting conditions |
|
| 图 6 温升曲线与耗散能曲线对比图 Fig.6 Comparison of temperature rise curve and dissipative energy curve |
PDC高速切削条件下,刀具前端面累积的热量比较少,并且温度基本保持缓慢上升。在井下作业中,温度升高后,金刚石台面上会随之产生高的拉应力,同时由于钻井液的冷却作用会导致金刚石层与硬质合金基体产生不同的收缩情况,加速裂纹的扩展。因此,通过提高切削速度控制刀具表面的温升情况,可以有效减小热冲击对PDC切削齿的影响,减少分层现象,从而延长PDC切削齿的使用寿命。
不同切削速度下的温升曲线如图 7所示。由图 7可以看出,当PDC刀具的切削速度在10.0 m/s时,刀具前端面温度在刚接触岩石阶段刀具与岩石表面出现高速摩擦和压碎作用,热量迅速累积,之后基本稳定且保持一个缓慢攀升的状态。并且,温度波动小另一方面也抑制了金刚石内部由于热膨胀系数不均带来的PDC分层的可能性[11]。因此就温升角度而言,PDC刀具在高速切削过程中,切削速度应该大于等于10.0 m/s。
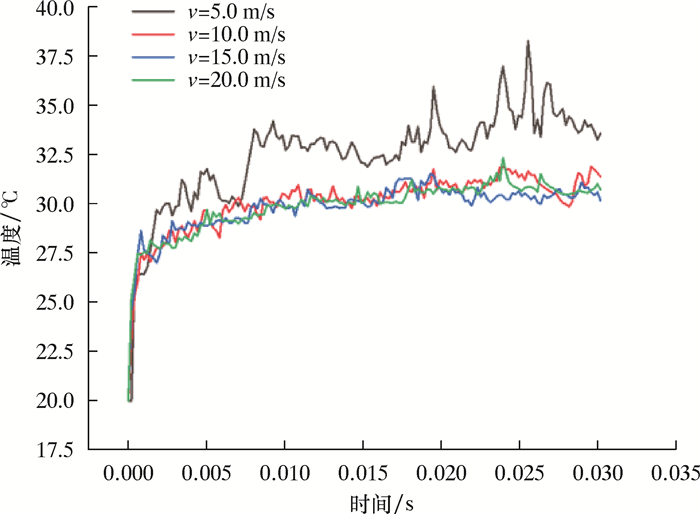
|
| 图 7 不同切削速度下的温升曲线 Fig.7 Temperature rise curves under different cutting speeds |
图 8为不同切削速度下切屑形成的第1个周期的温度云图。
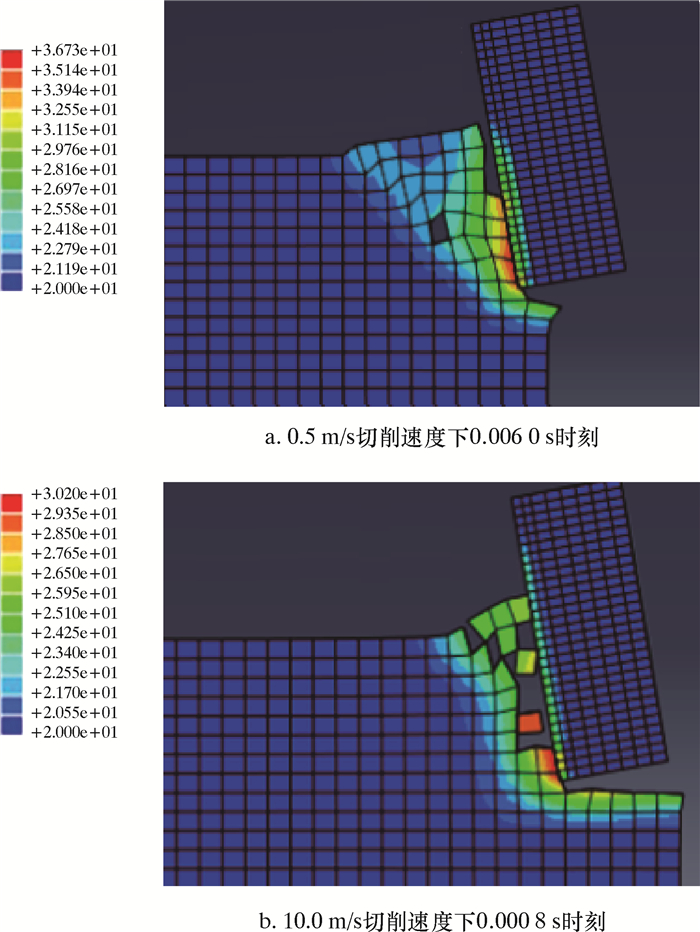
|
| 图 8 第1个切屑形成周期结束时模型温度对比图 Fig.8 Comparison of model temperature at the end of the first cutting formation cycle |
由图 8a可以看出,0.5 m/s切削速度条件下切削热主要集中在岩石与刀具接触附近,在岩石与刀具上温度基本相同。由图 8b可以看到,10.0 m/s切削速度条件下切削热主要集中在岩石与刀具接触附近的岩石上。另外,图中切屑上出现了明显的高温,并且某些部位温度会超过刀具与岩石接触位置的最高温度,这代表了切屑会带走大量的热量。由图还可以看出,0.5 m/s切削速度下形成大块岩屑的一个周期长,能量累积高,产生的切屑少,这也解释了为什么PDC刀具在常规切削速度切削岩石过程中,相对于高速切削条件刀具前端面积累的热量高。
2.3 高速切削对PDC刀具承受应力的影响各高速切削条件下实时刀尖应力数据如图 9所示。由图 9可知,切削过程中应力由于能量的累积和释放过程会表现为应力的周期性变化形式。这种高频的应力变化会导致冲击疲劳以及PDC切削齿内部的残余应力引起冲击震动,金刚石磨粒周围的粘结剂首先经受冲刷侵蚀和空化,然后遇到磨损和侵蚀的作用,最后PCD层在高温高压烧结后留下的残余应力会在PDC刀具受到高冲击力时导致宏观破裂[12]。
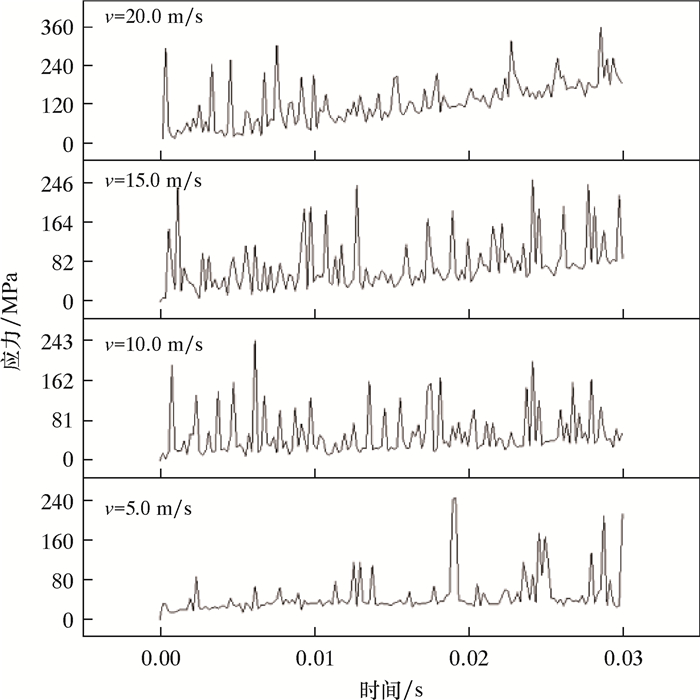
|
| 图 9 各高速切削条件下实时刀尖应力数据图 Fig.9 Real-time blade tip stress data for each high-speed cutting condition |
图 10为各切削速度下的应力平均值曲线和对应的机械比能曲线。从图 10可以看出,从常规切削速度提升到10.0 m/s的高速条件过程中平均应力缓慢升高,其对应的机械比能迅速下降。在刀具与岩石切削过程中,应力主要影响了刀具的使用寿命。机械比能主要表征了刀具切削过程中的切削效率,机械比能越低,单位进尺所需能量越小,切削效率越高。从图 10还可以看出,单纯从应力增量和机械比能角度上考虑,最佳切削速度应该设计在5.0~10.0 m/s之间。

|
| 图 10 各切削速度下的应力曲线和机械比能对比图 Fig.10 Comparison of stress curve and mechanical specific energy at each cutting speed |
图 11为各切削速度下应力标准差和偏度的曲线图。应力标准差表示应力的绝对稳定性;偏度表示应力数值相对于平均值的稳定值,表示应力的相对稳定性,可以客观评价数据稳定性。
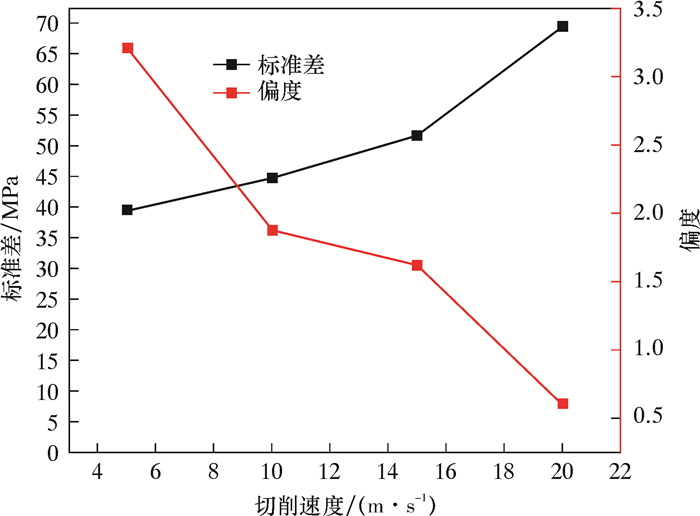
|
| 图 11 各切削速度下应力标准差和偏度对比图 Fig.11 Comparison of stress standard deviation and skewness at each cutting speed |
从应力稳定性以及尽量降低冲击损伤对PDC切削齿影响的角度来看,在切削速度5.0~15.0 m/s阶段,应力标准差缓慢攀升而应力偏度在10.0~15.0 m/s阶段保持一个相对稳定的低值,因此,最佳切削速度应该设计在10.0~15.0 m/s之间。
3 结论(1) 切屑的大小和形成过程分析表明,当切削速度超过岩石的临界切削速度时,以压碎作用为主的塑性破岩方式开始转化为以切削作用为主的脆性破坏形式,在这个阶段下切削力更加稳定,能量积累时间更短,更利于破碎岩石,这个临界转化速度在0.5~5.0 m/s之间。
(2) 温度的角度分析表明,由于常规速度切削相对于高速切削,能量累积时间长,切屑小,温度逸散不畅,所以PDC刀具在常规切削速度切削岩石过程中,相对于高速切削条件刀具前端面积累的热量高。
(3) 应力和机械比能角度的分析表明,从常规切削速度提升到10.0 m/s的高速条件过程中平均应力缓慢升高,其对应的机械比能迅速下降。此外,在切削速度5.0~15.0 m/s阶段,应力标准差缓慢攀升而应力偏度在10.0~15.0 m/s阶段保持一个相对稳定的低值,因此,最佳切削速度应该设计在10.0~15.0 m/s之间。
(4) 结合温升曲线、应力增量、机械比能、应力稳定性以及切屑表征的破坏模式等多角度分析,高速切削背景下适宜的切削速度在10.0 m/s左右。
| [1] |
许利辉, 毕泗义. 国外PDC切削齿研究进展[J]. 石油机械, 2017, 45(2): 35-40. XU L H, BI S Y. Overseas researches on PDC cutters[J]. China Petroleum Machinery, 2017, 45(2): 35-40. |
| [2] |
查春青, 枊贡慧, 李军, 等. PDC钻头扭转振动特性分析及减振工具设计[J]. 石油机械, 2017, 45(3): 1-5. ZHA C Q, LIU G H, LI J, et al. Analysis of torsional vibration characteristics of PDC bit and design of the damping tool[J]. China Petroleum Machinery, 2017, 45(3): 1-5. |
| [3] |
LIU W J, ZHU X H, LI B. The rock breaking mechanism analysis of rotary percussive cutting by single PDC cutter[J]. Arabian Journal of Geosciences, 2018, 11: 192. DOI:10.1007/s12517-018-3530-6 |
| [4] |
AKBARI B, MISKA S. The effects of chamfer and back rake angle on PDC cutters friction[J]. Journal of Natural Gas Science and Engineering, 2016, 35: 347-353. DOI:10.1016/j.jngse.2016.08.043 |
| [5] |
SCOTT T A. The influence of microstructure on the mechanical properties of polycrystalline diamond:a literature review[J]. Advances in Applied Ceramics, 2018(3): 161-176. |
| [6] |
张志军, 贾春德. 超高速切削机理的研究[J]. 沈阳工业学院学报, 1999, 18(1): 41-45. ZHANG Z J, JIA C D. Study on the mechanism of ultra-high speed cutting[J]. Journal of Shenyang Institute of Technology, 1999, 18(1): 41-45. DOI:10.3969/j.issn.1003-1251.1999.01.010 |
| [7] |
赵鹏, 赵旭. 超高速切削的技术体系、技术现状和发展趋势[J]. 应用技术, 2012(8): 84-87. ZHAO P, ZHAO X. Technical system, technology status and development trend of ultra-high speed cutting[J]. Applied Technology, 2012(8): 84-87. |
| [8] |
YARI N, KAPITANIAK M, VAZIRI V, et al. Calibrated FEM modelling of rock cutting with PDC cutter[C]. MATEC Web of Conferences 148, 16006, 2018.
|
| [9] |
YAN W. Single PDC cutter force modeling for hard rock cutting[M]. New Mexico: New Mexico Institute of Mining and Technology Socorro, 1997.
|
| [10] |
XUE J, XIA Y, JI Z, et al. Soft rock cutting mechanics model of TBM cutter and experimental research[C]//XIE M, XIONG Y, XIONG C, et al. Intelligent robotics and applications. Berlin Heidelberg: Springer, 2009: 383-391.
|
| [11] |
HARELAND G, YAN W, NYGAARD R, et al. Cutting efficiency of a single pdc cutter on hard rock[J]. Journal of Canadian Petroleum Technology, 2009(6): 60-65. |
| [12] |
MIN-SEOK B, HEE-SUB P. Effect of diamond particle size on the microstructure and wear property of high pressure high temperature (HPHT) sintered polycrystalline diamond compact (PDC)[J]. Korean Journal of Metals and Materials, 2017, 11: 790-797. |



