0 引言
修井机是修复油井产能的重要设备,具有移动速度快和作业效率高等优点,在提升油井采收率方面发挥着重大作用。据统计,修井作业中,小修作业时间占修井作业工作量的90%~95%,因此其作业安全性越来越受到用户的重视。
修井机在制动阶段,绞车等效力矩和等效惯动惯量的变化会产生大钩的制动加速度,造成井架的振动和冲击。过大的制动加速度对设备的安全运行产生风险,甚至造成井架倒塌等事故,造成巨大的人身和财产损失[1-4]。过小的制动加速度不仅影响作业效率,使得设备作业能力不能充分发挥,造成资源浪费,还会在紧急情况下无法及时刹车,产生严重的安全事故。
刹车系统目前多采用模块设计方法,经过多年发展,已取得较大进展,其中贾尚帅等[1]通过建立两自由度盘式刹车系统的动力学模型研究摩擦振动问题,陈建等[2]和黄粤川等[3]简化了现有通井机刹车系统结构,增强了刹车性能。但是修井机刹车性能不仅取决于刹车系统,还与井架、钢丝绳和作业工况等其他因素相关,因此需从整体上对刹车系统进行系统分析。
笔者通过对绞车滚筒在各工况条件下的制动分析,研究了修井机刹车系统参数与游车大钩制动加速度的关系。研究结果对于优化刹车性能参数具有一定的实际意义。
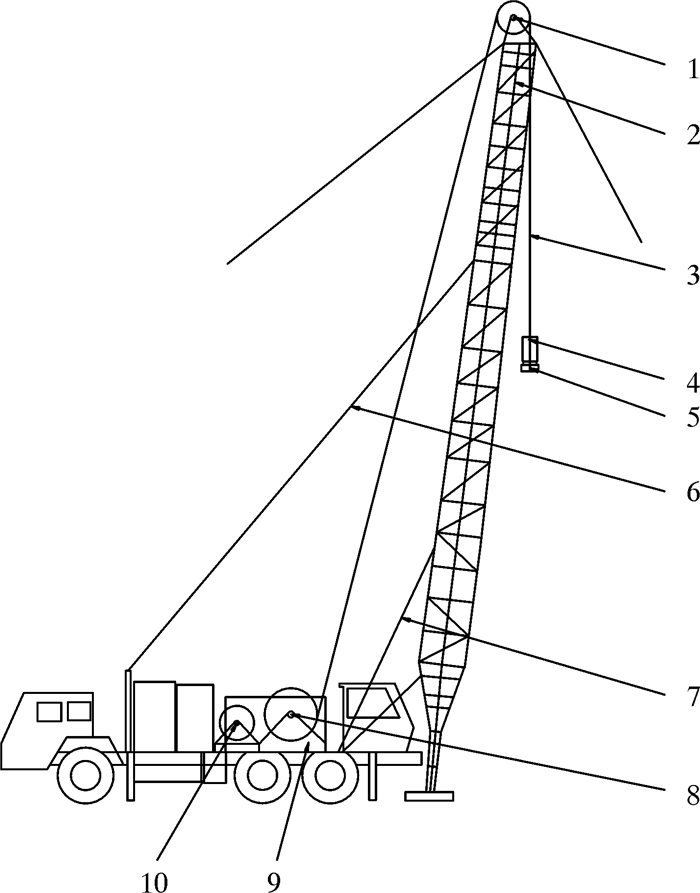
1 计算模型建立修井机起升系统主要由绞车、天车、游车、钢丝绳和井架系统等组成,其具体结构示意图如图 1所示[5-6]。
|
| 图 1 修井机起升系统结构示意图 Fig.1 Structural schematic of workover rig 1—天车;2—井架;3—钢丝绳;4—游车;5—大钩;6—绷绳;7—起升油缸;8—绞车;9—变速箱;10—电机。 |
作业时,通过吊环和吊卡把杆柱连接在游车大钩上,修井机刹车前游车大钩的运动状态比较简单,在绞车驱动力矩作用下,克服管柱的重力等载荷而产生相对运动;刹车时,刹车系统制动力矩作用于绞车的制动盘上,系统产生制动加速度,在制动期间绞车制动加速度将对井架、钢丝绳和大钩等构成的弹性系统产生激励而引起系统振动,产生较大的动载荷。
因此,依据机械动力学原理建立修井机的刚体动力学方程,求解游车大钩在制动过程中的制动速度和加速度,可以优化刹车力矩,达到制动过程对井架影响最小的目的[7]。
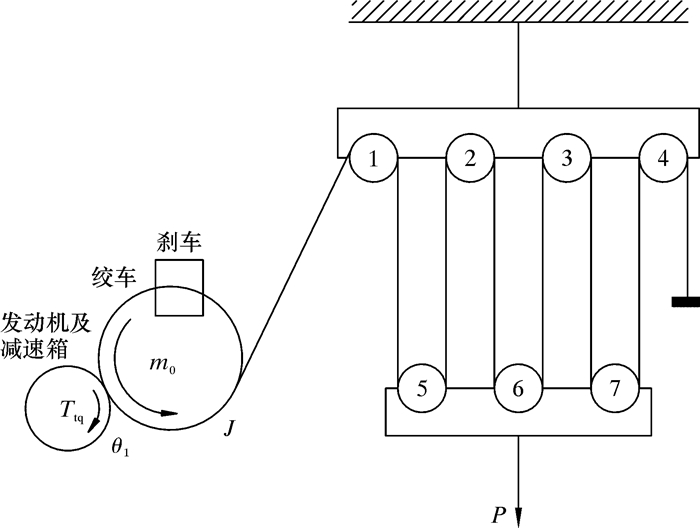
取绞车滚筒为等效构件,则修井机的物理模型可简化为如图 2所示。为了便于分析,做如下假设:①修井机传动系统中减速箱齿轮啮合过程中不考虑轮齿的弹性变形[8]。②不考虑机械系统钢丝绳重力及运动过程中的摩擦损失。③修井机绞车滚筒、井架、天车和游车大钩可等效为刚性质量体。④不考虑起升系统轴的横向振动及游车大钩水平方向位移[9]。⑤不考虑修井机作业过程中受到的外界影响。⑥忽略绞车滚筒运动过程中的钢丝绳缠绕半径变化。
|
| 图 2 修井机作业物理模型示意图 Fig.2 Schematic diagram of the physical model of the workover rig operation |
绞车滚筒等效动力学模型为:

|
(1) |
式中:Je为系统的等效转动惯量,kg·m2;Me为系统的等效力矩,N·m;$φ$1为绞车滚筒(等效动力学模型)的转角,rad;ωe为绞车的角速度,rad/s。
因此绞车的等效转动惯量为:
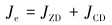
|
(2) |
式中:JZD为绞车滚筒和减速系统及电机轴等效到绞车轴上的等效转动惯量,kg·m2;JCD为游动系统等效到绞车滚筒轴上的等效转动惯量,kg·m2。
游动系统等效到绞车滚筒轴的转动惯量为:

|
(3) |
式中:ωi为各滑轮转速,rad/s;ω0为绞车转速,rad/s;Ji为各滑轮转动惯量,kg·m2;mi为各滑轮质量,kg;vi为游车大钩垂直方向速度,m/s;P为钩载,kN。
根据滑轮组工作原理[10],对游车大钩及轮系进行运动分析,即有:

|
(4) |
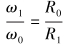
|
(5) |
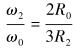
|
(6) |
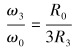
|
(7) |

|
(8) |

|
(9) |
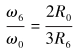
|
(10) |

|
(11) |
式中:Ri为各滑轮绳槽半径,m;R0为绞车滚筒有效半径,m。
假设天车和游车滑轮尺寸分别为Rt和Ry,将式(4)~式(11)代入式(3),得:

|
(12) |

|
(13) |
设修井机绞车滚筒(含制动毂)转动惯量为JG,减速器低速级轴系的转动惯量为JD1,中间轴系的转动惯量为JD2,高速轴系的转动惯量为JD3,电机的转动惯量为JD,联轴器的转动惯量为JL,减速系统总传动比为I,高速级的传动比为Ig2,低速级传动比为Ig1,则减速器低速轴的转动惯量可以表示为[11]:

|
(14) |
修井机下放阶段,作用在绞车滚筒上的等效驱动力矩为钩载对绞车的力矩,即:

|
(15) |
式中:v为钩载起升速度,m/s;α为游车大钩钩载P运动方向与重力方向的夹角,α=180°;ω为绞车角速度,rad/s。
计算可得:

|
(16) |
式中:R0为绞车滚筒半径,m;n′为修井机的有效绳数。
修井机制动系统利用摩擦原理制动,若不考虑刹车过程中摩擦盘的热效应、液压管路压力及大班司机踏板力波动[12-13],则理想的制动系统正常制动力矩信号应为斜坡响应,理想的紧急制动力矩信号应为阶跃响应,其制动参数为制动力矩增长率k和最大制动力矩T。
2 等效动力学方程求解根据动力学方程求解修井机制动过程的真实运动,因修井机制动时等效转动惯量是关于绞车滚筒位置的函数,等效力矩是关于时间的函数,无法利用解析法求解,所以可用数值法[14-15]迭代公式进行求解。
绞车滚筒等效转速为:

|
(17) |
游车大钩下放速度为:

|
(18) |
绞车滚筒等效制动加速度为:

|
(19) |
将上式代入,得:

|
(20) |
游车大钩下放制动加速度为:

|
(21) |
现场经验表明,决定刹车性能的因素主要有制动初速度v、钩载P、刹车力矩增长率k及最大力矩T等参数。为判断各因素对刹车系统影响的重要程度,利用正交分析法对各因素在不同工况进行分析。各因素水平如表 1所示。
| 水平 | v/(m·s-1) | P/kN | k/(N·m·s-1) | T/(kN·m) |
| 1 | 0.5 | 100 | 1 000 | 15 |
| 2 | 1.0 | 200 | 2 000 | 20 |
| 3 | 1.5 | 400 | 5 000 | 25 |
选取制动时间及最大制动加速度为评价指标,数值计算正常制动条件下9种工况制动时间及最大加速度,结果如表 2所示。表 2中,A、B、C分别代表试验中游车大钩制动初速度v、钩载P、正常制动刹车力矩增长率k在不同水平下的情况。
| 序号 | A | B | C | 试验结果 | |
| t/s | amax/(m·s-2) | ||||
| 1 | 1 | 1 | 1 | 8.3 | 0.12 |
| 2 | 1 | 2 | 2 | 6.2 | 0.17 |
| 3 | 1 | 3 | 3 | 4.1 | 0.27 |
| 4 | 2 | 1 | 2 | 6.0 | 0.35 |
| 5 | 2 | 2 | 3 | 4.2 | 0.54 |
| 6 | 2 | 3 | 1 | 8.3 | 0.24 |
| 7 | 3 | 1 | 3 | 3.8 | 0.80 |
| 8 | 3 | 2 | 1 | 8.3 | 0.37 |
| 9 | 3 | 3 | 2 | 6.0 | 0.52 |
正常制动工况下制动时间和最大制动加速度的极差分析如表 3所示。表 3中,Ki为各因素i水平所对应的试验数据之和,其大小可判定各因素优水平和优组合;ki为各因素i水平所对应的试验数据平均值;R为因素在各水平值下的试验数据极差值,反映试验数据随其因素水平的波动幅度,其大小可判定因素的主次顺序。
| 参数 | t/s | a/(m·s-2) | |||||
| v | P | k | v | P | k | ||
| K1 | 18.60 | 18.10 | 24.90 | 0.56 | 1.27 | 0.73 | |
| K2 | 18.50 | 18.70 | 18.20 | 1.13 | 1.08 | 1.04 | |
| K3 | 18.10 | 15.40 | 12.40 | 1.69 | 1.03 | 1.61 | |
| k1 | 6.20 | 6.03 | 8.30 | 0.19 | 0.42 | 0.24 | |
| k2 | 6.17 | 6.23 | 6.07 | 0.38 | 0.36 | 0.35 | |
| k3 | 6.03 | 5.13 | 4.03 | 0.56 | 0.34 | 0.54 | |
| R | 0.17 | 1.10 | 4.27 | 0.38 | 0.08 | 0.29 | |
正交试验中极差反映了各因素水平对指标影响的大小。在修井机正常制动过程中,制动力矩增长率的极差最大,因此它是影响制动时间的最主要因素,其他顺序依次为钩载和制动初速度。对最大制动加速度影响的主要顺序为制动初速度、制动力矩增长率和钩载。
紧急制动条件下制动时间及最大加速度如表 4所示。
| 序号 | A | B | C | 试验结果 | ||
| t/s | amax/(m·s-2) | |||||
| 1 | 1 | 1 | 1 | 1.63 | 1.18 | |
| 2 | 1 | 2 | 2 | 1.22 | 1.58 | |
| 3 | 1 | 3 | 3 | 0.98 | 1.97 | |
| 4 | 2 | 1 | 2 | 1.43 | 3.16 | |
| 5 | 2 | 2 | 3 | 1.15 | 3.96 | |
| 6 | 2 | 3 | 1 | 1.93 | 2.37 | |
| 7 | 3 | 1 | 3 | 1.24 | 5.94 | |
| 8 | 3 | 2 | 1 | 2.08 | 3.56 | |
| 9 | 3 | 3 | 2 | 1.57 | 4.73 | |
紧急制动工况下制动时间和最大制动加速度极差分析如表 5所示。
| 参数 | t/s | a/(m·s-2) | |||||
| v | P | T | v | P | T | ||
| K1 | 3.83 | 4.3 | 5.64 | 4.73 | 10.28 | 7.11 | |
| K2 | 4.51 | 4.45 | 4.22 | 9.49 | 9.10 | 9.47 | |
| K3 | 4.89 | 4.48 | 3.37 | 14.23 | 9.07 | 11.87 | |
| k1 | 1.28 | 1.43 | 1.88 | 1.58 | 3.43 | 2.37 | |
| k2 | 1.50 | 1.48 | 1.40 | 3.16 | 3.03 | 3.16 | |
| k3 | 1.63 | 1.49 | 1.23 | 4.74 | 3.02 | 3.96 | |
| R | 0.35 | 0.06 | 0.76 | 3.17 | 0.40 | 1.59 | |
修井机紧急制动过程中,最大制动力矩的极差最大,因此它是影响制动时间的主要因素,其次为制动初速度和载荷。对于最大制动加速度的影响主要顺序为制动初速度、最大制动力矩及钩载。
3.2 制动系统参数的确定小修作业机额定制动力矩的设计受到安全、效率及成本等因素的制约,制动系统的最大制动性能应在作业机额定载荷和额定下放速度的工况下进行计算。根据小修作业机钩载与下放速度关系图,假设额定制动载荷P=400 kN、制动初速度v=1 m/s的工况下,分别计算在正常制动及紧急制动条件下,以不同的制动力矩加载率k及最大制动力矩T时,大钩的制动时间t和最大制动加速度a,其计算结果如表 6所示。
| 正常制动 | 紧急制动 | |||||
| k/ (N·m·s-1) |
t/s | a/ (m·s-2) |
T/ (kN·m) |
t/s | a/ (m·s-2) |
|
| 1 000 | 7.65 | 0.24 | 10 | 2.92 | 1.58 | |
| 2 000 | 5.41 | 0.30 | 15 | 1.95 | 2.37 | |
| 3 000 | 4.42 | 0.41 | 20 | 1.46 | 3.16 | |
| 4 000 | 3.83 | 0.48 | 25 | 1.17 | 3.95 | |
| 5 000 | 3.43 | 0.54 | 30 | 0.97 | 4.74 | |
正常制动条件下,制动时间与最大制动加速度之间的关系如图 3所示。由图 3可知,正常制动过程中,假设制动力矩为线性增长,则随着制动力矩增长率的增加,游车大钩的制动时间减小,最大制动加速度增大,且当制动力矩增长率大于4 000 (N·m)/s时,对制动时间的影响作用减弱,而当制动力矩增长率在3 000 (N·m)/s左右时,最大制动加速度急剧升高,与现场经验一致,因此理想的制动力矩增长率取值范围为2 000~3 000 (N·m)/s。

|
| 图 3 正常制动时间-加速度关系图 Fig.3 Time-acceleration diagram of normal braking |
紧急制动条件下,制动时间与最大制动加速度之间的关系如图 4所示。由图 4可知,紧急制动过程中,假设为恒力矩制动方式,则随着最大制动力矩的增加,游车大钩的制动时间减小,最大制动加速度增大,且当最大制动力矩大于20 kN·m时,对制动时间的影响作用减弱,而最大制动加速度与制动力矩为线性关系,因此理想的最大制动力矩取值范围为15~20 kN·m。

|
| 图 4 紧急制动时间-加速度关系图 Fig.4 Time-acceleration diagram of emergency braking |
4 现场试验
为验证前面所建立的修井机刹车过程的数学模型及其计算方法的正确性,采用无线激光位移测试系统对游车大钩进行位移试验,采样频率1 000 Hz[16]。试验中,为减小试验数据误差,进行了多次重复试验,即修井机大钩由静止状态起升并进行3次刹车,其大钩初始下放速度1.5 m/s左右,利用激光位移传感器测试游车大钩下放过程中的位移,通过数值计算的方法,得到游车大钩的瞬时速度和加速度曲线。
试验选用胜利油田在役SHL5320TXJ修井机,修井机游车大钩测试原理及现场制动测试分别如图 5和图 6所示。

|
| 图 5 游车大钩测试原理图 Fig.5 Schematic diagram of the travelling block and hook test 1—绞车;2—钢丝绳;3—天车;4—井架;5—游车;6—大钩;7—测试反光板;8—杆柱;9—激光测距仪。 |

|
| 图 6 修井机现场制动测试图 Fig.6 Field test chart of workover rig brake |
修井机在30 kN钩载条件下制动,在该过程中,游车大钩实际制动速度和加速度曲线分别如图 7和图 8所示。由图 7和图 8可知,刹车过程历时8.3 s,游车大钩下放距离5.5 m,大班司机为了控制下放速度共进行3次刹车,该过程中最大制动加速度为0.58 m/s2。

|
| 图 7 游车大钩实际制动速度曲线 Fig.7 Actual braking speed curve of the travelling block and hook |

|
| 图 8 游车大钩实际制动加速度曲线 Fig.8 Actual braking acceleration curve of the travelling block and hook |
制动过程如下,制动测试在第71.1 s开始,大班司机在74.3 s时采取第一次制动,此时游车距离井口位移6.3 m,初始下放速度1.24 m/s,游车大钩下放速度迅速降低,为了保证作业效率,大班司机在第76.9 s时第一次减小制动力矩,直到第77.4 s时大班司机开始第二次制动,此时大钩位移距井口位移3.8 m,下放速度0.7 m/s,直到第78.0 s时第二次减小制动力矩,此时大钩位移距反光板3.4 m,下放速度0.4 m/s。由于大钩仍未下放完成,大班司机在第78.9 s时进行第三次制动,此时大钩与反光板位置为2.9 m,下放速度0.6 m/s,直到第80.8 s时,此时大钩距反光板位移为2.3 m,管柱下放到位,此时大钩速度为0,制动过程结束。
修井机刹车测试结果表明:若不考虑3次制动过程中游车大钩受到风载和作业冲击等因素的影响,以及钢丝绳和井架产生的振动,其游车制动加速度曲线均经过先增加后减小的过程,该过程与制动加速度理论计算值变化规律一致。修井机理论制动加速度处于紧急制动状态,且经历一次制动过程,其制动力矩为系统最大制动力矩,因此制动加速度最大为1.8 m/s2。实际制动测试过程中,大班司机操作受到大钩位移的影响,刹车目的是为了控制游车大钩下放速度,该过程为正常制动状态,因此其制动力矩随大钩位移的变化而变化,其最大制动加速度为0.58 m/s2。
5 结论(1) 利用刚体动力学原理结合修井机系统结构,搭建其系统动力学模型并进行求解,能够为修井机刹车系统合理选型及大班司机制定刹车参数提供重要参考。
(2) 在制动过程中制动力矩增长率是影响制动时间的最主要因素,而最大制动初速度是影响制动加速度的主要因素。
(3) 为实现游车大钩的制动时间与最大制动加速度的平衡,理想的制动力矩增长率取值范围为2 000~3 000 (N·m)/s,因此理想的最大制动力矩取值范围为15~20 kN·m。
| [1] |
贾尚帅, 丁千. 刹车系统的摩擦自激振动和控制[J].
工程力学, 2012, 29(3): 252-256.
JIA S S, DING Q. Self-excited vibration and control of braking system[J]. Engineering Mechanics, 2012, 29(3): 252-256. |
| [2] |
陈建, 李斌. 通井机刹车系统设计[J].
西南石油大学学报(自然科学版), 2007, 29(增刊2): 130-132.
CHEN J, LI B. The design of a tractor hoist braking system[J]. Journal of Southwest Petroleum University(Science Edition), 2007, 29(S2): 130-132. |
| [3] |
黄粤川, 郝正鹏. ZJ70DZ型钻机用伊顿436WCB型刹车失效分析[J].
石油矿场机械, 2006, 35(2): 82-83.
HUANG Y C, HE Z P. Failure analysis of Eaton 436WCB brake system of ZJ70DZ driller[J]. Oil Field Equipment, 2006, 35(2): 82-83. |
| [4] | MANSOUR H, AHMAD M M, DHAFR N, et al. Evaluation of operational performance of workover rigs activities in oilfield[J]. International Journal of Productivity and Performance Management, 2013, 62(2): 201-218. |
| [5] |
万邦烈.
采油机械的设计计算[M]. 北京: 石油工业出版社, 1994.
WAN B L. Design calculation of oil extraction machine[M]. Beijing: Petroleum Industry Press, 1994. |
| [6] |
冯定, 杨志远, 柳进, 等. 液压修井机现状与发展趋势[J].
石油机械, 2010, 38(1): 69-72.
FENG D, YANG Z Y, LIU J, et al. Present situation and development trend of hydraulic workover rig[J]. China Petroleum Machinery, 2010, 38(1): 69-72. |
| [7] |
綦耀光, 石临嵩, 王国东. 前置式气平衡抽油机失载时运动与动力分析[J].
石油大学学报(自然科学版), 1991, 15(5): 47-52.
QI Y G, SHI L S, WANG G D. Motion and dynamic analysis of front air balanced pumping unit under no-load load[J]. Journal of Petroleum University (Science Edition), 1991, 15(5): 47-52. |
| [8] |
张梅军, 曹勤.
工程机械动力学[M]. 北京: 国防工业出版社, 2012.
ZHANG M J, CAO Q. Engineering machinery dynamics[M]. Beijing: National Defense Industry Press, 2012. |
| [9] |
刘庆.交流变频电驱动钻机起升系统动载特性研究[D].东营: 中国石油大学(华东), 2008. LIU Q. Study on dynamic load characteristics of AC variable frequency electric drive drilling rig lifting system[D]. Dongying: China University of Petroleum(East China), 2008. |
| [10] | ZHOU N, LIU K. A tunable high-static-low-dynamic stiffness vibration isolator[J]. Journal of Sound and Vibration, 2010, 329(9): 1254-1273. DOI: 10.1016/j.jsv.2009.11.001 |
| [11] |
何仁, 王晶, 胡东海. 永磁式缓速器的制动力矩分级结构设计[J].
吉林大学学报(工学版), 2015, 45(4): 1056-1062.
HE R, WANG J, HU D H. Design of braking torque grading structure for permanent magnet retarder[J]. Jilin University Journal, 2015, 45(4): 1056-1062. |
| [12] |
于淼, 石博强. 液压制动系统中蓄能器的优化设计与稳健分析[J].
农业工程学报, 2011, 27(6): 132-135.
YU M, SHI B Q. Optimization design and robust analysis of accumulator in hydraulic brake system[J]. Transaction of the Chinese Society of Agricultural Engineering, 2011, 27(6): 132-135. DOI: 10.3969/j.issn.1002-6819.2011.06.024 |
| [13] | WOLFGANG F, GEORG F, MARIO E, et al. Electro hydraulic brake system for motor vehicle: 6817381B2[P]. 2001-11-16. |
| [14] |
汪建晓, 孙学强, 靳龙.
机械原理[M]. 武汉: 华中科技大学出版社, 2017.
WANG J X, SUN X Q, JIN L. Mechanical principle[M]. Wuhan: Huazhong University of Science and Technology Press, 2017. |
| [15] | DRESIG H, HOLZWEIBIG F. Machine dynamics[M]. Beijing: Science Press, 2012. |
| [16] | PEDRO M, SILVA B. Anoveriew and a contribution to the optical measurement of linear displacement[J]. IEEE Sensors Journal, 2001, 1(4): 322-332. DOI: 10.1109/7361.983472 |




